J. Cent. South Univ. Technol. (2011) 18: 438-443

DOI: 10.1007/s11771-011-0715-5

Attenuation of wave propagation in a novel periodic structure

ZHENG Ling(郑玲)¹, LI Yi-nong(李以农) ¹, A. BAZ²

1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;

2. Department of Mechanical Engineering, University of Maryland, College Park, MD20742, USA

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: A novel periodic mount was presented. A theoretical model was developed to describe the dynamics of wave propagation in the novel periodic mount. The model was derived using Hamilton’s energy conservation principle. The characteristics of wave propagation in unit cell were analyzed by transfer matrix formulation. Numerical examples were given to illustrate the effectiveness of the periodic mount. The experiments were carried out to identify the predications of the theoretical model. The obtained results show that the experimental results coincide with the prediction of theoretical model. No pass bands appear in the overall frequency range measured when waves propagate in the longitude direction of the periodic mount. These dramatic results demonstrate its potential as an excellent mount in attenuating and isolating vibration transmission.

Key words: periodic structure; vibration isolation; passive mount

1 Introduction

A periodic structure consists of an assembly of identical elements connected in a repeating array which form a complete structure together [1]. Examples of such structures can be found in many engineering applications. They include satellite solar panels, wings and fuselages of aircraft, petroleum pipe-lines, railway tracks, and many others. Each such structure has a repeating set of stiffeners, placed at regular intervals. The study of periodic structures has a long and rich history spanning more than 300 years. Typically, the studies have been related to crystals, optics, and the like. It is only recently that the wave motion in periodic structures has been studied. Such structures have a salient feature that waves can propagate through the structure in some frequency bands (pass bands) and are attenuated in others (stop bands). MEAD and his co-workers [2-6] should be mentioned due to their pioneering efforts in the study of the dynamics of periodic structures including many original contributions. Excellent reviews on the state-of- the-art have been given by MEAD [7] and by MESTER and BENAROYA [8], where extended lists of references can be found. Since then, studies on the characteristics of periodic structures and their applications in engineering have been extensively investigated including passive and active periodic structures [9-14]. More realistically, applications involved helicopter gearbox support strut [15], tail rotor drive shaft bearing [16], helicopter blade [17] and so on.

Mounts play an important role in supporting structural mass and isolating noise and vibration transmission. In general, three types of mounts are used to isolate noise and vibration transmission. They are passive mounts such as conventional rubber mounts, semi-active mounts such as magnetorheological (MR)/ electrorheological (ER) mounts as well as active mounts. Usually, active mounts have high control performance in a wide frequency range. However, active mounts require many sensors to control the system, high power consumption, and more complicated devices. Although conventional passive mounts are simple in structure and economic in cost, their performance is limited to a narrow frequency range.

In this work, a novel passive mount with periodic structure is presented to isolate and attenuate noise and vibration transmission in a wider frequency range, especially in low frequency range. The dynamic mechanical filtering characteristics of the novel periodic mount are exhibited theoretically and experimentally. Experimental performances of the mount verify the effectiveness of this type of passive periodic mounts and are in agreement with the prediction of the theoretical model. Stop bands of wave propagation cover the overall frequency range, and this means that the attenuation of vibration can be extended to all frequencies. Therefore, a simple, economic and excellent mount is obtained.

2 Mathematical modeling of periodic mounts

2.1 Overview

Fig.1(a) shows a schematic drawing of the novel periodic mount which is made of identical cells in the longitudinal direction. Each cell can be divided into four elements. These elements are numbered 1, 2, 3 and 4 from the right to the left (see Fig.1(b)). Elements 1, 3, 4 can be regarded as one-dimensional rods approximately, thus the dynamics of these elements can be determined using the classical transfer matrix method. However, element 2 has a complicated structure which cannot be regarded as one-dimensional rod, therefore, the important point of the theoretical model is to find out the transfer relationship between the left and right side of element 2. The equation of motion for element 2 can be derived by applying Hamilton’s principle. The boundary conditions are given to determine the transfer relationship of element 2 in details. Once the transfer relationship of element 2 is obtained, the transfer matrix of one cell can be obtained by the product of a series of the transfer matrices for different elements in the cell.

2.2 Transfer relationship of element 2

2.2.1 Main assumptions

It is assumed that the shear strains in the rectangle cross section core are negligible. It is also assumed that the longitudinal stresses in the visco-elastic layer are negligible. The transverse displacements of all the points on any cross section of the periodic mount are not considered. Furthermore, core and outer layer are assumed to be elastic and dissipate no energy whereas the visco-elastic layer is assumed to be linearly visco- elastic.

2.2.2 Geometry relationships

From the geometry of Figs.1(b) and (c), the shear strain γ in the visco-elastic material is given by

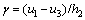                              (1)

where u₁ and u₃ are the longitudinal deflections of the aluminium core and outer aluminium layer, respectively. h₂ defines the thickness of visco-elastic layer.

2.2.3 Energies of element 2

The potential energies associated with the longitudinal extension of the aluminium core and two outer layers and the shear of two visco-elastic layers sandwiched between the core and the outer layers are expressed as

              (2)

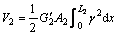                          (3)

where K₁=E₁A₁, K₃=E₃A₃, are the axial stiffnesses of the core and the outer layer, respectively. E₁ and E₃ denote the elastic moduli of the core and the outer layer, respectively. A₁ and A₃ are the cross section areas of them, respectively, A₁=h₁b, A₃=2h₃b. b is the width of the core and the outer layer. Also, G₂ denotes the storage shear modulus of the visco-elastic layer and A₂ is the cross section area of the visco-elastic layer, A₂=2h₂b.

The kinetic energy T associated with the longitudinal deflection u₁ and u₃ is given by

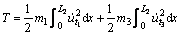                (4)

where m₁ and m₃ are the masses per unit length of the core and outer layer, respectively. m₁=r₁A₁, m₃=r₃A₃ where r₁, r₃ are densities of the core and the outer layer, respectively.

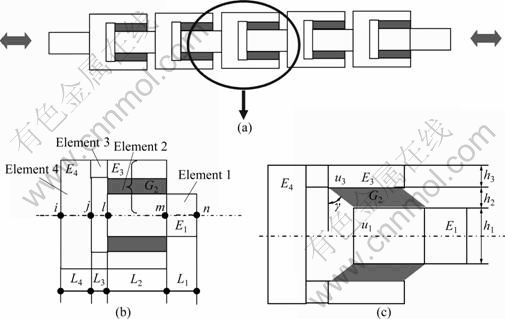
Fig.1 Schematic drawing of periodic mount and main parameters: (a) Periodic mount; (b) Undeflected; (c) Deflected

The work W dissipated in the visco-elastic layers is given by

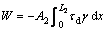                           (5)

where τ_d is the dissipative shear stress developed by the visco-elastic layers.

τ_d is given by

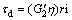                                (6)

where η and i denote the loss factor of the visco-elastic layers and 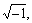 respectively.

2.2.4 Equation of motion and boundary conditions

The equation of motion and boundary conditions governing the operation of element 2 are derived by applying Hamilton’s principle:

                    (7)

where δ(·) denotes the first variation in the quality inside the parentheses.

The resulting equations of motion are

K₁u_1xx-m₁u_1tt-2bG₂/h₂(u₁-u₂)=0                  (8)

K₃u_3xx-m₃u_3tt+2bG₂/h₂(u₁-u₂)=0                  (9)

where 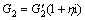 is the complex modulus of the visco-elastic material.

Transformed into frequency domain, Eqs.(8) and (9) become

            (10)

            (11)

For element 2, the above equations are subjected to the following boundary conditions:

At x=0: u_1x=0                               (12)

At x=L₂: u_3x=0                               (13)

2.2.5 Transfer relationship of element 2

Eqs.(10) and (11) can be put in the following state-space form:

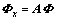                                  (14)

where

and

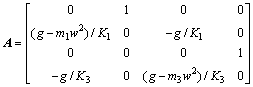
where g=2bG₂/h₂.

The solution of Eqs.(10) and (11) is given by

                       (15)

where  and 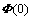 are given by

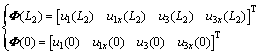   (16)

The computation of the exponential matrix exp(AL₂) in Eq.(15) can be carried out using the scaling and squaring algorithm of METLAB with a Pade approximation to ensure efficient convergence. The computation result of the exponential matrix exp(AL₂) is expressed as

           (17)

From the boundary conditions given by Eqs.(12) and (13), then combined with Eq.(17), Eq.(15) is reduced to

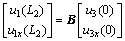                       (18)

where

                (19)

It is noted that Eq.(18) gives out the relationship between the left side and the right side of element 2.   represents the displacement and strain in the right side, while  represents the displacement and strain in the left side. Therefore, the following relationship can be obtained:

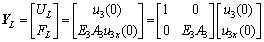   (20)

  (21)

The transfer matrix T of element 2 can be computed by Eqs.(18), (20) and (21):

T_element2Y_L=Y_R                               (22)

             (23)

2.3 Transfer matrices of elements 1, 3 and 4

Elements 1, 3 and 4 can be regarded as one- dimensional rods with different cross section areas; therefore, their equations of motion have the similar form:

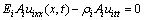 (i=1, 3, 4)            (24)

Transformed into frequency domain, Eq.(24) is rewritten as

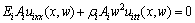 (i=1, 3, 4)    (25)

Eq.(25) can be put in the following state-space form:

Z_ix=P_iZ_i (i=1, 3, 4)                           (26)

where

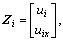
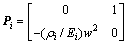              (27)

The solution of Eq.(26) leads to

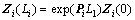                      (28)

Define a new state vector Y_i which includes the traction force F_i:

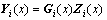                          (29)

where 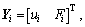 is the transfer vector at x, and

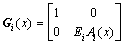                        (30)

From Eq.(29), the transfer matrix representation is given by

   (31)

2.4 Transfer matrix of periodic mount

Now, the transfer matrix of unit cell can be computed as

T_cell=T_element1×T_element2×T_element3×T_elment4          (32)

and for the complete periodic mount

                               (33)

where N_cell is the number of cells in the periodic mount. Thus, all the information about the propagation characteristics is given by the eigenvalue λ of the transfer matrix T:

                       (34)

where μ is the propagation constant, α and β are called attenuation factor and phase angle and represent the real portion and imaginary portion of the propagation constant, respectively.

3 Performance of periodic mount

3.1 Materials

The entire periodic mount is made of two materials; one is aluminium, and the other is rubber, as shown in Fig.1. The geometric and physical properties of them are given in Table 1 and Table 2.

Table 1 Geometric properties

Table 2 Physical properties

3.2 Propagation of waves in periodic mount

Fig.2 demonstrates a comparison of the filtering characteristics between the periodic structure with four cells and nonperiodic structure with the same length. Figs.2(a) and (b) represent the phase angle of propagation constants and the attenuation factor of propagation  constants, respectively. It can be seen that no pass band appears in the entire frequency range for the novel periodic structure. It is also noted that no stop band appears in the whole frequency range for uniform aluminium rod. This dramatic results show that the propagation of waves in the new periodic structure along the longitudinal direction is completely impeded. In general speaking, it is very difficult for passive mounts to attenuate the vibration in the whole frequency domain. Usually, stop bands are limited to high frequencies for most of periodic mounts. The results look like a little bit strange. In fact, it is completely possible because no longitudinal connection occurs between the core and the outer layer. Wave propagation characteristics of the novel periodic mount imply its potential application as an excellent mount. Fig.3 displays a numerical comparison of transfer function amplitude between the periodic and nonperiodic mounts. It can be seen that a significant attenuation of vibration occurs in the entire frequency range.

3.3 Experimental identification

In order to identify the prediction of theoretical model, a series of experiments are performed. Two experimental frames are designed and manufactured: one is used to measure the transfer function amplitude of the periodic mount, and the other is used to determine the transfer function amplitude of the conventional nonperiodic mount. Fig.4 shows their configurations. Fig.5 shows the experimental setup used for testing the effectiveness of the periodic mount proposed. It can be seen that the frame with four passive periodic mounts is used to measure the vibration transmission from the upper plate which is excited by a shaker to the base plate.

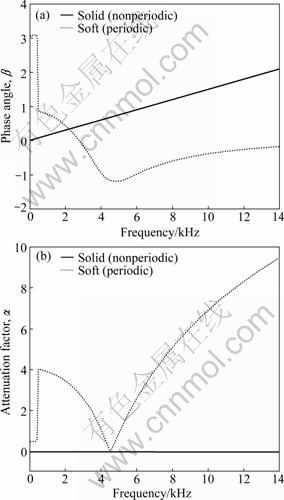
Fig.2 Propagation constants for periodic and uniform mount:  (a) Phase angle; (b) Attenuation

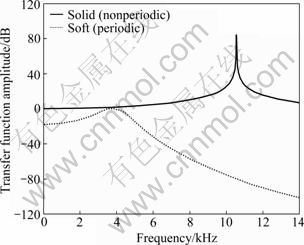
Fig.3 Numerical transfer function amplitudes obtained by theoretical model

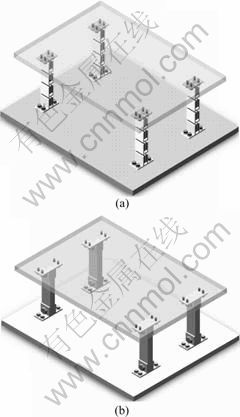
Fig.4 Configurations of frames measured with different mounts: (a) Periodic mount; (b) Conventional nonperiodic mount

Fig.5 Experimental setup

Each periodic mount is made of four cells. Piezoelectric accelerometers (PCB Model 303A3) are located in each end of one periodic mount. One is used to measure the acceleration produced by the shaker at the top of the mount. The other is used to capture the acceleration at the bottom of the mount. A spectrum analyzer (ONE SOKKI Model CF910) is used to record the signal coming from the accelerometers. Fig.6 shows the experimental transfer function amplitude between the input excitation as applied to one end of the mount and the transmitted acceleration to the other end of the mount.

It can be observed that the experimental results are in agreement with the prediction of theoretical model. It can be clearly seen that the stop bands cover the whole frequency range from the low frequencies to high frequencies, and no pass bands appear. The attenuation of vibration is obvious and effective for all frequencies. The characteristics of propagation of waves in this novel mount demonstrate its promising application as an excellent mount.

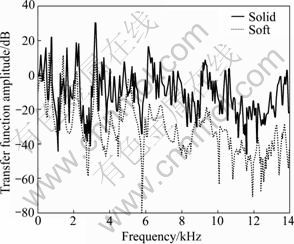
Fig.6 Experimental transfer function amplitude

4 Conclusions

1) A novel passive mount with periodic structure is presented. A theoretical model is developed to describe the dynamics of wave propagation in the novel mount. The model is derived using Hamilton’s principle. A cell of the periodic mount is divided into four elements; the transfer matrix formulation for each element is given; overall transfer matrix of unit cell is obtained by multiplying the transfer matrices of the four elements. The characteristics of wave propagation in four series of cells are analyzed by transfer matrix formulation.

2) Numerical examples are given to illustrate the effectiveness of these periodic mounts. The experiments are performed to identify the predication of the theoretical model. Both of theoretical and experimental results show that stop bands cover the overall frequency range from the low frequency to high frequency measured, and no pass bands appear. The passive mounts presented here supply an excellent and invaluable means to extend the working frequency range of conventional passive mounts to a wide frequency range in an easy and simple way.

3) The presented mounts can find many applications such as gearbox support struts, engine mounts in automobiles and aircrafts as well as underwater vehicles. The design and manufacture of a prototype practice mount using the concept of the novel periodic mount presented here is a natural extension of further work.

References

[1] BAZ A. Active control of periodic structures [J]. ASME Journal of Vibration and Acoustics, 2001, 123: 472-479.

[2] MEAD D J. Free wave propagation in periodically supported, infinite beams [J]. Journal of Sound and Vibration, 1970, 11(2): 181-197.

[3] MEAD D J. Vibration response and wave propagation in periodic structures [J]. ASME Journal of Engineering for Industry, 1971, 21: 783-792.

[4] MEAD D J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling [J]. Journal of Sound and Vibration, 1973, 27(2): 235-260

[5] MEAD D J. Wave propagation and natural modes in periodic systems: Ⅰ. Mono-coupled systems [J]. Journal of Sound and Vibration, 1975, 40(1): 1-18.

[6] MEAD D J. A new method of analyzing wave propagation in periodic structures: Applications to periodic Timoshenko beams and stiffened plates [J]. Journal of Sound and Vibration, 1986, 104(1): 9-27.

[7] MEAD D J. Wave propagation in continuous periodic structures: Research contributions from Southampton, 1964-1995 [J]. Journal of Sound and Vibration, 1996, 190(3): 496-524.

[8] MESTER S, BENAROYA J. Periodic and near periodic structures: Review [J]. Shock and Vibration, 1995, 2(1): 69-95.

[9] RUZZENE M, BAZ A. Active control of wave propagation in periodic fluid-loaded shells [J]. Smart Materials and Structures, 2001, 10: 893-906.

[10] SOLAROLI G, GU Z, BAZ A, RUZZENE M. Wave propagation in periodic stiffened shells: Spectral finite element modeling and experiments [J]. Journal of Vibration and Control, 2003, 9(9): 1057-1081.

[11] THORP O, RUZZENE M, BAZ A. Attenuation of wave propagation in fluid-loaded shells with periodic shunted piezoelectric rings [J]. Smart Materials and Structures, 2005, 14: 594-604.

[12] RUZZENE M, BAZ A. Control of wave propagation in periodic composite rods using shape memory inserts [J]. Journal of Vibration and Acoustics, Transactions of ASME, 2000, 122: 151-159.

[13] THORP O, RUZZENE M, BAZ A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches [J]. Smart Materials and Structure, 2001, 10: 979-989.

[14] TOSO M, BAZ A. Wave propagation in periodic shells with tapered wall thickness and changing material properties [J]. Shock and Vibration, 2004, 11: 411-432.

[15] SINGH A, PINES D J, BAZ A. Active/passive reduction of vibration of periodic one-dimensional structures using piezoelectric actuators [J]. Smart Materials and Structures, 2004, 13: 698-711.

[16] RICHARDS D, PINES D J. Passive reduction of gear mesh vibration using a periodic drive shaft [J]. Journal of Sound and Vibration, 2003, 264: 317-342.

[17] TAWFIK M, CHUNG J, BAZ A. Wave attenuation in periodic helicopter blades [C]// Jordan International Mechanical Engineering Conference (JIMEC). Amman, Jordan, 2004: 26-28.

(Edited by YANG Bing)

Foundation item: Project(50775225) supported by the National Natural Science Foundation of China

Received date: 2009-08-06; Accepted date: 2009-12-23

Corresponding author: ZHENG Ling, Professor, PhD; Tel: +86-23-65106094; E-mail: zling@cqu.edu.cn