J. Cent. South Univ. Technol. (2011) 18: 874-880
DOI: 10.1007/s11771-011-0776-5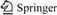
Mechanism of grout bulb expansion and its effect on ground uplifting
ZHANG Min(章敏), WANG Xing-hua(王星华), WANG You(汪优)
School of Civil and Architectural Engineering, Central South University, Changsha 410075, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to study the uplifting effect of compensation grouting on ground surface and the upper structures, the ground heave induced by stratum expansion was considered as a stochastic process and the stochastic medium theory was applied to determine the heave and deformation of ground surface under uniform and non-uniform expansion models of spherical grout bulb. The corresponding calculating formulas and simplified methods were derived based on the hypotheses of radial expansion. Then, a numerical model, in which radial velocity was imposed on the outer nodes of grout bulb to simulate the expansion process reaching a required volume strain, was established simultaneously. This new method avoids repeated trial calculation needed in the traditional method which applies a “fictitious” expanding pressure in the grouting elements. The results show that the numerical solutions have good consistency with the theoretical ones. Meanwhile, though the heave resulting from non-uniform expansion is larger than that from uniform expansion for shallow grouting, both of them tend to be convergent with the increasing of grouting depth.
Key words: grouting; ground surface uplifting; stochastic medium theory; numerical simulation
1 Introduction
During the construction of metro station in urban built-up areas, both deep excavation and well-points dewatering would induce subsidence of surrounding ground and further cause damage to nearby structures and environmental hazards. Adopting compaction grouting or fracturing grouting under the foundation is demonstrated to be an effective measure to compensate the ground loss and heave the existing buildings. Several cases of compaction grouting to successfully control foundation settlement and to lift and re-level settled structures were reported in Refs.[1-3]. GRAF [4] found that the grouting pressure during injecting would make conical shear failure occur in the soil above grout bulb as the soil around grouted zone is compressed to reach a maximal degree. And the compaction effect was influenced by the weight of the soil cone above the grout bulb, together with the shear strength of soil. PRASENJIT et al [5] investigated the surface upheaval in the case of inclined compaction grouting which was treated to be an inclined cylinder with grout pressure acting on its peripheral surface based on the elastic continuum approach. And the impacts of grout column length and inclination as well as the depth of grout injection were analyzed simultaneously. By applying an internal pressure to zero-thickness interface elements embedded in mesh, WISSER et al [6] simulated the compaction grouting to arrest the foundation settlement caused by adjacent tunnel excavation. This approach was used by TANG et al [7], who proposed to increase the volume strain of grouting elements by applying a “fictitious” expanding pressure to achieve the heaving effect, and employed software FLAC3D to study an existing tunnel heaving by grouting during the construction of the Chongwenmen subway station of Beijing Metro Line 5.
Though some new findings were found from the above points of view, most current papers are basically descriptions or summaries on special engineering cases and the detailed mechanics of heave by grouting is not well understood. Furthermore, because of the mixed geological compositions of the soil and the complexity of the ground movement which is controlled by a large number of known and unknown factors, finding closed form analytic solutions becomes a harder sometimes an impossible task by the classical elastic-plastic analysis. The method of probability statistics using the stochastic medium theory may get better results, which is desirable to be a simple but rational way with considering the soil as random medium.
In this work, assuming grouting region as a spherical grout bulb and considering the soil movement owing to the radial expansion of grout bulb as a stochastic process, the deformation formulas of ground surface under both uniform and non-uniform deformation models were derived based on the stochastic medium theory. Moreover, a numerical model was established by reaching an assigned volume strain in the grouting elements to realize the expansion process and the results were compared with the theoretical solutions.
2 Theoretical solution of surface uplifting by grouting
2.1 Ground movement due to elemental expansion
According to the stochastic medium theory, the ground heave by grouting can be regarded as a stochastic process and a reverse process of surface subsidence due to excavation. Fig.1 shows an elemental expansion with dual coordinate systems: one for global coordinate (x, y, z) and the other for local coordinate (ξ, ζ, η). The elemental expansion has dimensions of dξ×dζ×dη. According to YANG et al [8] and LIU [9], the heave, We(x, y), at a point (x, y) in the global coordinate system due to an elemental expansion with depth z can be expressed as
 (1)
(1)
where β is the angle of influence zone, and can be attained through the back analysis method or referring to the width of the uplifting volume on the surface.
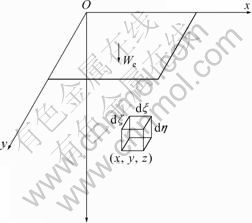
Fig.1 Sketch of elemental expansion
Equation (1) is the basic formula for developing the equations of ground surface movement by grouting. The total surface heave, W(x), can be obtained finally by accumulating all the tiny heaves induced by the expansion of infinitesimal elements in the entire grouting region.
2.2 Ground uplifting and deformation due to grouting
Because of the densification and replacement effects for soil by compaction grouting, the pores of soil are assumed to be completely occupied by slurry in the grouting region. Two proposed deformation patterns of grout bulb are shown in Fig.2: uniform expansion and non-uniform expansion. In Fig.2(a), a radical uniformed expansion of ΔR of the gout bulb with a spreading radius R, and the center of which is located at a depth of H0, is assumed to occur in all directions. A rotational heave surface which is symmetrical with the vertical axis through the center of grout bulb would be generated. For convenience, all the following derivations are conducted with the spherical coordinate system.
Fig.2 Ground uplifting by expansion of grout bulb: (a) Uniform expansion; (b) Non-uniform expansion
Based on the previous method together with the principle of superposition, the surface heave, W(A), inclination, T(A), and curvature, K(A), at a point away from the symmetrical axis of a distance, A, could be expressed individually as follows:
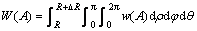 (2)
(2)
 (3)
(3)
 (4)
(4)
where
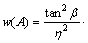
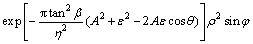 (5)
(5)

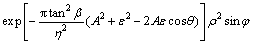 (6)
(6)
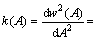

 (7)
(7)

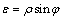
As all the displacements are symmetric with the spherical center for this sphere symmetric problem, only the radial displacement would happen, whereas the tangential displacement is impossible [10]. By resolving the radial displacement of ground surface induced by the expansion into both the vertical and horizontal displacements, the horizontal displacement, U(A), can be obtained:
 (8)
(8)
The above formulas of ground deformation are based on the uniform radial movement around the grout bulb. However, the grouting pressure in practice, which is influenced by many factors such as soil characteristics, spreading extent of slurry, is not the same in various directions. That is, the radial deformation is not uniform but oval-shaped, as shown in Fig.2(b), even for the ideal condition that the grout bulb bears the same radial expansion pressure. The boundary condition of the prescribed displacement shown in Fig.3 for this case is illustrated as
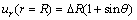 (9)
(9)
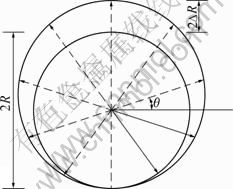
Fig.3 Boundary condition of non-uniform deformation patterns
It should be noted that the prescribed displacements equal 2ΔR at the crown and zero at the bottom of the grout bulb. In fact, such model can be obtained through moving the grout bulb up a distance of ΔR under the uniform expansion model. By following the same principle and reason, the heave of ground surface can be written as

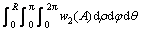 (10)
(10)
where
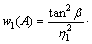
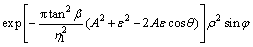 (11)
(11)
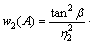
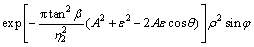 (12)
(12)


ε= ρsinφ
Through substituting η in Eqs.(6)-(7) by η1 and η2, respectively, the inclination and curvature of ground surface could be obtained with reference to the previous derivation method. The expressions are not listed here for limited space.
Although the discrepancy of both deformation patterns on the heave is not obvious for deep grouting, the solutions with non-uniform radial expansion model are better to coincide with the numerical results in general and closer to the actual situation than the traditional uniform deformation model. Furthermore, the actual expansion pattern of the grout bulb which is influenced by the initial state of stress, the stress-strain behavior of soil, the grouting pressure, the rheological properties of slurry and the construction technique should be diverse and vary considerably. The deformation assumptions shown in Fig.3 are ideal situations and cannot perfectly represent all cases, but the non-uniform expansion model is no doubt a better choice in comparison with the traditional uniform expansion model.
2.3 Simplified solutions
As the three integrands Eqs.(5)-(7) in the prior triple integrals are non-integrable functions, some corresponding simplified solutions are induced in the following analysis in order to avoid coding tedious numerical integration program and be easily applied. According to Ref.[11], with the ratio of the grouting depth to the diffusion radius of slurry beyond a certain value, the whole increased volume of grout bulb by expression, in relation to the surrounding soil, can be considered as an infinitesimal body. That is to say, the whole integration region can be simplified into an infinitesimal element as mentioned in Section 2.1. So, the heave by uniformed expansion can take the following simplified form:
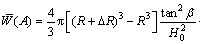

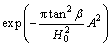 (13)
(13)
Similarly, the simplified forms of the horizontal displacement, inclination and curvature can be rewritten as

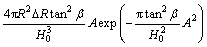 (14)
(14)
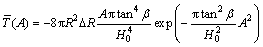 (15)
(15)
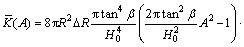
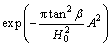 (16)
(16)
The volume increment of grout bulb before and after grouting for the non-uniform expansion pattern, regardless of the second and higher-order terms, can be expressed approximately by

 (17)
(17)
This indicates that the variation of the volume with the non-uniform radial expansion is the same as that of the uniform expansion. Consequently, the simplified surface heave and deformation formulas with both deformation patterns are almost identical and merely relevant to the volume strain as well as the depth of grout bulb, not depending on which deformation pattern is chosen.
3 Numerical simulation of surface uplifting by grouting
At present, researches in this area of uplifting effect using numerical simulation have generally been based either on the use of a “prescribed strain” approach to model grout injection or, alternatively, a “prescribed pressure” approach. In the “prescribed strain” approach, the grout injection is simulated by imposing appropriate values of strain on the elements representing the grouted soil. Such approach was described by NICOLINI and NOVA (2000) [12], HELMUT et al (2004) [13] and GOLEGGER (2001) [14]. With the “prescribed pressure” approach, the injection process is modeled by the application of “fictitious” internal pressure to the “grouting elements”. After finishing the injection, the stiffness of these elements is increased to an appropriate value. Some numerical schemes adopting this type of approach were described in Refs.[6-7, 15]. However, in order to reach the assigned volume strain for grout bulb, a series of trial calculations are necessary through adjusting the magnitude of pressure, which would cost much time and affect the efficiency especially for complicated mesh. Therefore, the “prescribed strain” approach is adopted in the analyses described in this work.
To simulate the expansion procedure by grouting in FLAC3D, an assigned radial velocity is exerted on the nodes of the outer face of the grout bulb and the number of run-steps can be determined forehand to avoid the trial calculation. With the method, the node velocity of various magnitude and direction can be assigned to the specified region to achieve isotropic or anisotropic expansion such as the cases of spherical, ellipsoidal or cylindrical grouted zone as well as the fracture grouting where the slurry spreads along a specified direction.
4 Results and discussion
4.1 Comparison of different methods
In order to demonstrate the correctness of the analytic formulas, a 3D numerical analysis used by the finite difference program FLAC3D [16] is carried out to investigate the uplifting effect by grouting. The center of the spherical grout bulb with a radius of 1.5 m is assumed to be located at a depth of 5 m. The overall dimensions of the model boundaries comprise a width of 6-times grout bulb radius from the central frame and the final sizes are -10 m≤x≤10 m, -10 m≤y≤10 m and -5 m≤ z≤5 m. As illustrated in Fig.4, the finite difference mesh utilized in the analysis consists of 3 120 brick- elements and 3 353 nodes. At the bottom level of the computational domain, all movements are restrained; while at the lateral external sides, lateral movements perpendicular to the boundary are prohibited. The soil is assumed to be elastic-plastic and governed by the Mohr- Coulomb constitutive model with an elastic modulus of 10 MPa and Poisson ratio of 0.35. And the volume strain of grout bulb is assumed to be 10%, being equivalent to be a radial displacement of 5 cm under the uniformed deformation pattern.
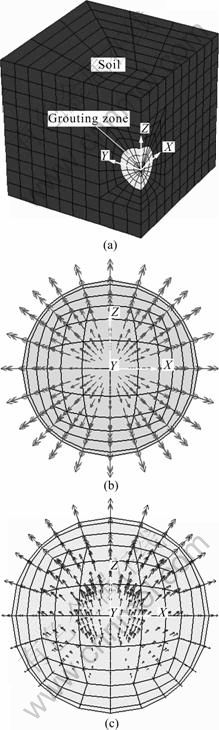
Fig.4 Finite difference mesh and expansion pattern of grout bulb: (a) Quarter mesh; (b) Uniform expansion; (c) Non-uniform expansion
Figure 5 depicts the displacement distributions under both expansion patterns. It can be seen that the soil at the top of grouting zone moves upward, while the soil below the region is squeezed and moves downward. Among the different depths, being closer to the grouting zone would cause a larger displacement peak.
Figures 6 and 7 present the theoretical results of surface heave and deformation with both expansion models and comparisons to the simplified and numerical solutions. Comparison of the peaks of heave and horizontal displacement between stochastic medium theory and the simplified results shows that their relative errors are merely about 5.8% and 1.0%, respectively. The results of other points on the surface are in substantial agreement with each other, thus verifying the validity of the simplified approach. However, in comparison with the analytic solutions shown in Figs.6(a)-(b) and Figs.7(a)-(b), the numerical results are slightly lower globally. The reason which may clarify the discrepancy lies in that the heave volume of ground surface in numerical simulation, which is identical with the expansion volume of grout bulb for no matter what soil condition using stochastic medium theory, is less than the assigned expansion volume which would be partly offset by the compression volume of surrounding soil due to stress redistribution. The application of the non-uniform deformation model would lead to a smaller error between the theoretical results and the numerical ones, and can be better to represent the actual expansion condition. It can also be seen that the horizontal displacement and inclination increase with the distance to the asymmetrical axis and almost reach the maximum values at 3 m simultaneously, then decrease gradually until tend to zero as illustrated in Figs.6(c) and (d). The distances where both of them reach the peak values are normally deemed identical.

Fig.5 Displacement distribution under both expansion patterns: (a) Uniform expansion; (b) Non-uniform expansion

Fig.6 Surface movement and deformation caused by uniform expansion: (a) Surface uplifting; (b) Surface horizontal displacement; (c) Surface inclination; (d) Surface curvature
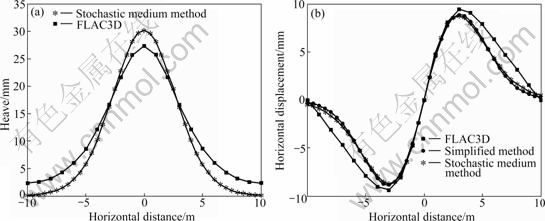
Fig.7 Surface movement and deformation caused by non-uniform expansion: (a) Surface uplifting; (b) Surface horizontal displacement
4.2 Impact of deformation pattern on displacement distribution
In order to study the impact of both deformation patterns on the surface heave with different grouting depths using the stochastic medium method, four groups of heave curves with H0=5, 8, 10 and 15 m are illustrated in Fig.8. The results with the non-uniform expansion pattern, on the whole, are greater than the ones with the uniform expansion pattern. The discrepancy of heaves attained by both models is apparent for shallow grouting and the curves appear narrow and deep. Both methods give almost the same magnitudes of heave and the curves become wide and shallow for deep grouting. This is to say, the impact of self-deformation pattern of grout bulb on the heave is significant when the grouting is relatively shallow, which is worthy of noticing during the in situ grouting. Moreover, since the results with simplified method in this work are identical regardless of deformation model applied, and merely rely on the quantity of radial expansion, the simplified method has better fitness under the condition of deep grouting.
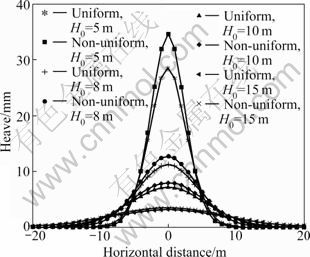
Fig.8 Influence of deformation patterns on heave with different grouting depths
5 Conclusions
1) The developed simplified method can predict reasonably well the grouting-induced ground heave profiles by the stochastic medium theory with both the deformation patterns. It appears to be convenient for application due to its brief form.
2) Due to the discrepancy induced by the case whether the soil compression is considered or not, the numerical results are slightly lower than the analytic solutions globally. However, the application of the non-uniform expansion pattern with both methods can make errors at a relative lower level and is better for the analysis. The method of modeling expansion by imposing velocity on nodes is feasible and convenient.
3) In comparison with the uniform deformation model, the heave peak with the non-uniform deformation model is greater for the case of shallow grouting, while the results under both conditions are almost identical for deep grouting.
References
[1] JAMES C N, CHENG W C. Grout efficiency of lifting structure in soft clay [C]// Soil and Rock Instrumentation, Behavior, and Modeling. Virginia: ASCE, 2009: 1-8.
[2] YANG Xiao-li, ZOU Jin-feng. Cavity expansion analysis with non-linear failure criterion [J]. Proceedings of the ICE-Geotechnical Engineering, 2011, 164(1): 41-49.
[3] YANG Xiao-li, ZOU Jin-feng. Estimation of compaction grouting pressure in strain softening soils [J]. Journal of Central South University of Technology, 2009, 16(4): 653-657.
[4] GRAF E D. Compaction grout [C]// Grouting, soil improvement and geosynthetics [J]. Reston, VA: ASCE, GSD, 1992, 1(30): 275-287.
[5] PRASENJIT B, MADHAV M R, PREZZI M. Estimation of heave due to inclined compaction grouting [C]// Advances in Ground Improvement Research to Practice in the United States and China. Florida: ASCE, 2009: 234-241.
[6] WISSER C, EAUGARDE C, BURD H J. Numerical modeling of compensation grouting above shallow tunnels [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2005, 29: 443-471.
[7] TANG Zhi-wei, ZHAO Cheng-gang, ZHANG Ding-li. Design of displacement grouting and prediction of the effect for construction of underground structures [J]. China Civil Engineering Journal, 2007, 40(8): 79-84. (in Chinese)
[8] YANG J S, LIU B C, WANG M C. Modeling of tunneling-induced ground surface movements using stochastic medium theory [J]. Tunnelling and Underground Space Technology, 2004, 19: 113-123.
[9] LIU Bao-chen. Ground surface movements due to underground excavation in China [C]// Comprehensive Rock Engineering. New York: Pergamon Press, 1993: 781-817.
[10] TIMOSHENKO S P, GOODIER J N. Theory of elasticity [M]. 3rd ed. New York: McGraw Hill, 1970: 125-145.
[11] YANG Xiao-li, WANG Jin-ming. Ground movement prediction for tunnels using simplied procedure [J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462-471.
[12] NICOLINI E. NOVA R. Modeling of a tunnel excavation in a non-cohesive soil improved with cement injections [J]. Computers and Geotechnics, 2000, 27: 2149-2172.
[13] HELMUT F, SCHWEIGER, KUMMERER C. Numerical modeling of settlement compensation by means of fracture grouting [J]. Soils and Foundations, 2004, 44(1): 71-86.
[14] GOLEGGET J. Numerical and analytical studies of the effects of compensation grouting [D]. Austria: Graz University of Technology, 2001.
[15] ADDENBROOKE T, ONG J, POTTS D M. Finite-element analysis of a compensation grouting field trial in soft clay [J]. Proceedings of the Institution of Civil Engineers, Geotechnical Engineering, 2002, 115(1): 47-58.
[16] FLAC3D-User’s manual [M]. Minneapolis, MN: Itasca Consulting Group Inc, 2005.
(Edited by PENG Chao-qun)
Foundation item: Project(2007AA11Z134) supported by the National High Technology Research and Development Program of China; Project(10JJ4035) supported by the Natural Science Foundation of Hunan Province, China; Project(2010ybfz046) supported by the Fund of Excellent Doctoral Dissertation of Central South University, China
Received date: 2010-03-19; Accepted date: 2010-09-09
Corresponding author: WANG Xing-hua, Professor, PhD; Tel: +86-731-82655489; E-mail: xhwang@mail.csu.edu.cn