DOI: 10.11817/j.issn.1672-7207.2015.09.009
基于干扰抑制和非线性摩擦力补偿的速度环PI控制器抗饱和设计
王慎航，王云宽，胡建华，秦晓飞，郑军，刘娜
(中国科学院大学 自动化研究所，北京，100190)
摘要：针对永磁同步电机速度调节器积分饱和导致动态品质变差的问题，提出一种新型的抗饱和(AW)设计方法。该AW方法首先把模型的不确定性视为系统的干扰；然后为了改善系统性能和提高抗干扰能力，在比例积分(PI)控制策略基础上，对速度环设计一种基于摩擦模型补偿和扰动观测补偿的复合控制方法；最后把PI控制器退饱和后从比例(P)模式重新进入PI模式的系统响应看作是带有初始值的系统响应，同时利用时域下的系统误差动态响应方程推导出系统无超调的误差和积分条件，当系统进入饱和时，系统以最大加速度运行，直到满足条件才重新进入PI模式，并给积分赋初始值。研究结果表明：该方法确保退饱和系统的优良的动态性能和无超调运行。与现有条件积分方法及其改进的方法相比，仿真和实验结果验证该新型AW 设计的可行性及优越性。
关键词：永磁同步电机(PMSM)；抗积分饱和；PI速度控制器；非线性摩擦力；干扰观测器；无超调
中图分类号：TP276 文献标志码：A 文章编号：1672-7207(2015)09-3224-07
Anti-windup design for PI-type speed controller based on nonlinear compensation and disturbance suppression
WANG Shenhang, WANG Yunkuan, HU Jianhua, QIN Xiaofei, ZHENG Jun, LIU Na
(Institute of Automation, University of Chinese Academy of Sciences, Beijing 100190, China)
Abstract: In order to solve the problem of dynamic quality deterioration caused by the proportional plus integral (PI) integral saturation of speed regulator in permanent magnet synchronous motor servo system, a novel anti-windup(AW) design was proposed. Uncertainties in the mode were regarded as a disturbance of the system by the AW method firstly. Then in order to improve the system low performance and disturbance rejection property a compound control method, which combined model-based friction compensation with disturbance observer compensation, was designed for speed loop based on PI control strategy. Finally, the desaturation system response of re-entering the PI mode from proportional (P) mode was used as a system response with an initial value, and the error and integral value condition which ensured the system non-overshoot were derived using dynamic responses of the system error equation in time-domain. When the system was saturated, it ran at maximum acceleration. Until the condition was satisfied, the PI mode was re-entered and an initial value was assigned to the integrator. The results show that this method ensures the desaturation system excellent dynamic performance and non-overshoot operation. Compared with the existing conditional integration and its improved methods, the simulated and experimental results demonstrate the feasibility and advantage of the new AW design.
Key words: permanent magnet synchronous motor (PMSM); anti-windup; PI speed controller; nonlinear friction; disturbance observer; non-overshoot
永磁同步电机(PMSM)以其体积小、功率密度大、低速输出转矩大、效率高、维护简单而被广泛应用于数控，轨道车辆等中[1]。PI控制由于其控制算法简单、鲁棒性好、易于实现等优点，已经被广泛的应用于永磁同步电机交流调速系统。电流环作为调速系统内环，保证了系统的动态响应速度，而速度环作为外环给电流环产生电流指令。速度环给出的电流指令值往往要进行限幅，因为电机最大电流限制、逆变器保护以及驱动装置过热保护的要求。由于PI控制器的设计往往是在系统线性区而忽略了饱和的限制。因此，当系统饱和时，PI控制器往往失去了调节的作用，并导致系统大的超调、调节时间长、震荡甚至不稳定问题，这种现象称为积分饱和现象[2-4]。为了克服积分饱和现象，许多抗饱和技术被提出，其中有一些运用非线性方法抑制饱和现象[5-7]，但是这增加了系统的复杂度，失去了PI控制器简单易实现的特点。因此，典型的抗积分饱和做法是增加积分饱和补偿装置。实质上，传统的抗饱和方法主要分为2类[8]：一类是条件积分方法，另一类是反计算方法。条件积分方法是当控制器饱和时关闭积分，当控制器退出饱和时重新开启积分。反计算方法是将控制器的输出与被控对象的输入之差构成反馈支路来减小积分量的输入，达到抑制积分饱和现象的目的。为了确保系统退饱和后无超调的动态品质，一些学者进一步地提出了其他控制技术。Choi等[9]针对有2个负实数极点的调速系统提出来一种方法，具体是当系统从P模式到PI模式转换时，赋予积分初始值来消掉系统的1个极点，系统成为一阶系统，保证了系统退饱和后响应的无超调。Hwi等[10]采用积分稳态的预测值作为PI模式重启时的积分初始值来抑制超调。同时，在现有的系统建模方法中，往往忽略了系统的摩擦力、外界干扰及模型的不匹配，把模型建立成线性系统模型，并在此模型的基础上设计了AW方法。很显然，这种设计思想虽然在理论上能够取得理想的结果，但是由于摩擦力[11-12]和干扰[13-14]的影响，控制效果也将大幅下降。为了解决现存方法的问题，本文作者提出一种新颖的AW算法。该方法首先改变传统的建模方法，考虑基于非线性摩擦力的补偿和干扰抑制，有效地抑制模型的不确定性。然后把退饱和重新进入PI模式的系统响应看作是带有初始值的系统响应，同时利用时域下的系统误差动态响应方程推导出系统无超调的误差和积分值条件，当系统重新进入PI模式时给积分赋初始值。该方法确保退饱和系统的优良的动态性能和无超调运行。与现有方法相比，仿真和实验结果验证该新型AW 设计的可行性及优越性。
1 基于摩擦力补偿和干扰抑制的误差模型建立
为了快速地跟随速度环误差指令，在伺服系统设计中往往要求电流环的带宽远大于速度环的带宽，这样电流内环就可看做1个常数放大器。不考虑系统干扰和噪声，那么速度环伺服系统可以简化为一阶系统
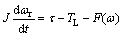
其中：τ=kTiq，为控制力矩；kT为力矩常数；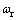
为电机转速；TL为负载力矩；
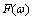为摩擦力，包含线性和非线性摩擦力。与传统的建模方法相比，式(1)增加了非线性摩擦力的建模，显然这增加了系统的非线性因素，但它更能准确地描述系统的动态响应，这有利于基于模型的饱和算法更加准确地实现。
1.1 摩擦力的补偿
Stribeck摩擦模型[11]在动态补偿中应用比较广泛，能够有效地描述线性和非线性摩擦力，是由库仑力、黏性摩擦力和静态摩擦力组成
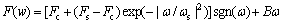
式中：Fc为库仑摩擦力；Fs为静态摩擦力；B为黏性摩擦力因数；
为润滑参数；
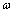为电机转速。若控制系统中控制输入量按照式进行摩擦力的补偿，则
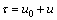
其中：u0为摩擦力补偿输入；u为新的控制输入量。将式代入式，系统中将没有摩擦力的非线性特性，得到线性的关系
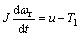
1.2 基于干扰观测器(DOB)的干扰抑制
为了抑制外部干扰以及高频噪声，在反馈控制的基础上进一步地加入了干扰观测器，如图1所示，其中：d，ζ和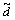
分别为干扰、噪声和干扰的估计值。为了便于问题的分析和模型的建立，本文将系统的模型不匹配归于系统的干扰[13]，那么系统对象可建立为P=Pn。其中：P为实际控制对象；Pn为名义模型对象。进而可得到控制外环传递函数：
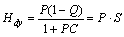
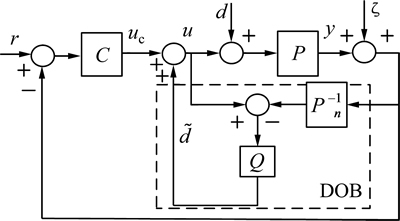
图1 带有DOB的反馈控制系统
Fig. 1 Feedback control system with DOB
其中：S和T分别为外环灵敏度和补灵敏度函数；C为外环控制器；Q为滤波器。式说明干扰回路的加入对于外环的输入输出控制没有影响，这也从理论上说明了外环的设计完全不受干扰观测器的影响。但从式和可以看出C和Q同时影响着系统干扰对外环的输出，因此，在设计干扰观测器时应同时兼顾C和Q的作用。本文采用低通滤波器
其中：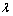
为时间常数；s为复参数。
1.3 误差模型建立
由于干扰补偿不影响外环，因此外环可以独立设计，将式化为
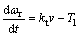
其中：kt=kT/J；Tl=TL/J；v为力矩电流且由下式决定
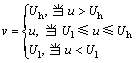
其中：Uh 和Ul分别为补偿摩擦力后电机的最大正电流和最小负电流，很显然这2个值随着摩擦力变化而变化。Uh和Ul按照下式选取，保证了Uh和Ul为常数，事实上摩擦力非常小，Uh和Ul不会影响系统的电流驱动能力。
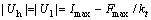
小命令参数下，设PI控制器表达式如下：
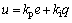
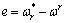
其中：kp为比例系数；ki为积分系数；q为误差的积分；e为系统的跟踪误差。e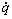的表达式为
的表达式为
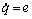
当PI控制器工作在线性区时，将式和代入式得
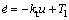
联合式和并进行Laplace变换得[10]
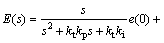
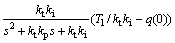
记为
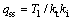
式所示为积分环节的稳态值，将式代入式整理得
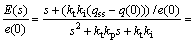
其中：a0=(ktki(qss-q(0)))/e(0)。
2 基于误差初始值模型的抗积分饱和方案的设计
2.1 基本原理
由式可以看出：当PI控制器由P模式进入PI模式时，式可以看作带有初始值，幅值为e(0)的脉冲响应。通过式容易看出系统的响应与积分和误差初始值有关，因此选择合适的q(0)和e(0)能够使退饱和后系统获得无超调的性能。
2.1.1 当系统有1对共轭极点
当系统具有1对共轭极点时，式可以化为
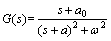
其中：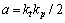
；
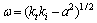；G(s)为控制对象传递函数；a0为控制系统零点。
对式进行Laplace逆变换可得时域的响应函数为
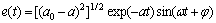
其中：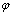
。
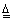
由式可以看出误差响应曲线函数为幅值逐渐减小的正弦曲线，这表明对于含有共轭极点的系统，无论怎样取值都不能满足无超调性的运行。
2.1.2 当系统有1对相等的负实极点
当系统有1对相等的负实极点时，式化为
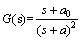
其中：a=ktkp/2。同样经过Laplace变化后得到时域的误差响应函数为
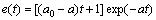
显然若a0＜a，系统必然产生超调；而当a0＞a时，系统不产生超调；若令a=a0，则式将变为
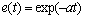
显然，系统也将无超调运行。
2.1.3 当系统有一对不等的负实极点
当系统有一对负实极点时，式化为
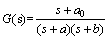
其中：
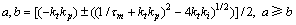
同样可得到时域的误差响应函数为
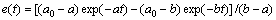
由式可以看出：若令a0=a或a0=b系统将具有式的响应函数形式；其中a0=b时(a＜b)，本方法和文献[9]基于频域中误差反馈提出的方法结果相同。事实上，当系统有1对相等和不等的负实极点时，令a0=a或a0=b本质上是a0的取值产生零极点相消，虽然能够取得无超调系统的运行，然而这将会导致：系统的固有频率改变，有可能导致震荡；有可能导致系统的过冲，尤其是在主导极点被消除，另外1个极点又远离原点时；会导致系统的不完全可控可观。因此，为了避免以上的不足，由时域响应表达式可知若令
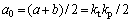
则式可化为
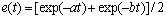
显然，式保留了系统的极点特性，同时也克服了以上的不足。
当系统有1对相等的负实极点(a0＞a)时，若a0在a的邻域取值，对系统的影响和零极点相消相似；若a0在远离a的邻域取值，显然系统响应将变慢，因此很难选择1个合适的a。为了避免这些问题，同时结合以上分析，可根据控制系统性能要求通过零极点配置的方法使系统具有2个负实数极点，同时零点满足式，这将保证退饱和后系统的无超调性能。
2.2 重启PI条件和积分初始值的确定
由于控制器是在饱和状态下运行，因此，由P模式进入PI模式的临界条件应满足控制器的输出仍然处于饱和状态，同时联立式得
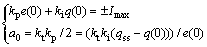
当系统运行在正的最大值条件下时
当系统运行在负的最大值时
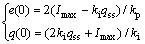
式(29)和(30)就是积分器重新开启的条件和初始值，具体的实施方案如图2所示。图2中未标明摩擦力补偿和干扰观测器。系统饱和时，开关S打开，关闭积分作用；然后S根据式(29)和式(30)重新打开，进而重启积分作用，同时赋予积分初始值保证无超调运行。
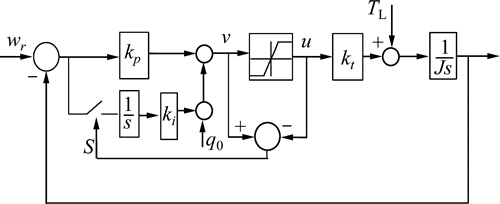
图2 提出的速度PI 控制器AW方案
Fig. 2 Proposed antiwindup PI speed controller scheme
3 仿真与实验
为了验证本文算法的有效性，在Matlab/simulink和基于DSP28335的伺服平台上分别进行仿真和实验验证。采用电机的具体参数为：定子电阻R=1.6 Ω；电感Ld=16.03 mH；Lq=17.15 mH；永磁磁链φf= 0.231 Wb；转动惯量J=1.1 g·m2；模型不匹配量△J= 2.2×10-4 kg·m2；极对数P=3；额定转速n=3 000 r/min；额定电流为6.5 A；力矩常数kT=0.692 N·m/A。Stribeck摩擦力模型参数辨识的方法有很多，本文采用曲线拟合的方法[12]，参数的计算可由稳态下测得的摩擦力矩并且联合最小二乘方法进行计算，辨识的参数为：Fc=0.005 77 N·m，Fs=0.007 4 N·m，B=0.000 242 (kg·m2)/s，ws=0.000 4 rad/s，|Uh|=|Ul|=6.42 A，辨识的Stribeck模型曲线如图3所示。仿真和实验均在空载条件下进行，速度指令为2 000 r/min，测速方法采用M/T方法[15]。同时，kp=0.1，ki=12，滤波器Q中λ=0.002。对比实验采用了Choi的方法和条件积分方法。仿真时采用的干扰d=0.02sin(2πt) N·m，高频噪音采用每个采样周期随机产生±1个脉冲。仿真和实验结果分别如图4和图5所示。
从图4和图5仿真和实验结果可以看出：每种方法的仿真结果曲线和实验结果曲线都有一些区别，这主要是因为仿真时采用的干扰，噪声和模型的不匹配量与实际不同导致的，但是仍然可以看出大致的轨迹曲线趋势与实际轨迹曲线相类似，仍能够验证算法的
有效性。因此，通过仿真和实验结果表明：
1) 本文提出的方法速度响应无超调运行，说明了该方法能够很好的抑制干扰，噪声和模型的不确定性。而Choi的方法虽然在理论上实现系统的无超调运行，但是由于干扰，噪声和模型的不确定性导致了取得的效果大幅下降。而条件积分方法，与其他2种方法相比，超调最大。
图3 摩擦模型的曲线拟合
Fig. 3 Curve fitting of friction model
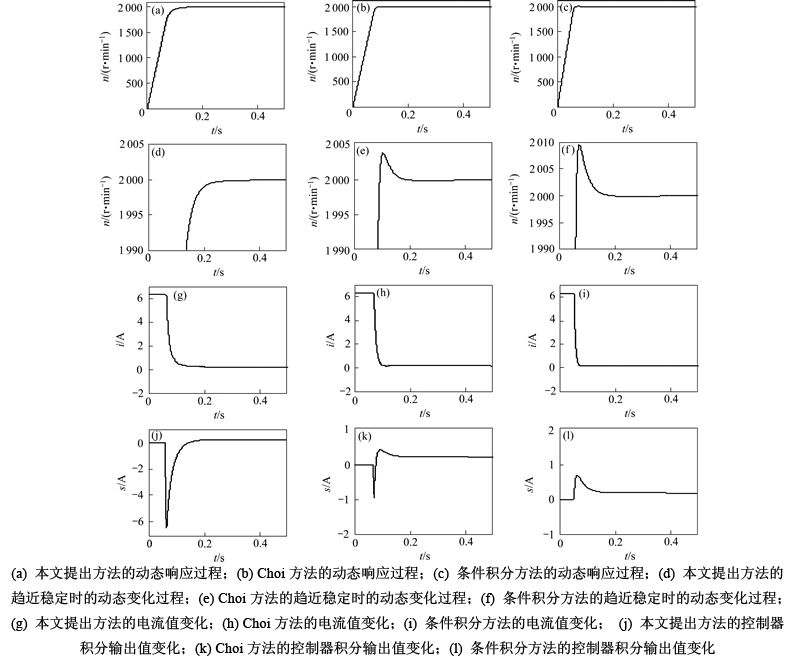
图4 永磁同步电机不同抗饱和方法的速度响应仿真结果
Fig. 4 Simulation results of PMSM for speed responses with different anti-windup methods
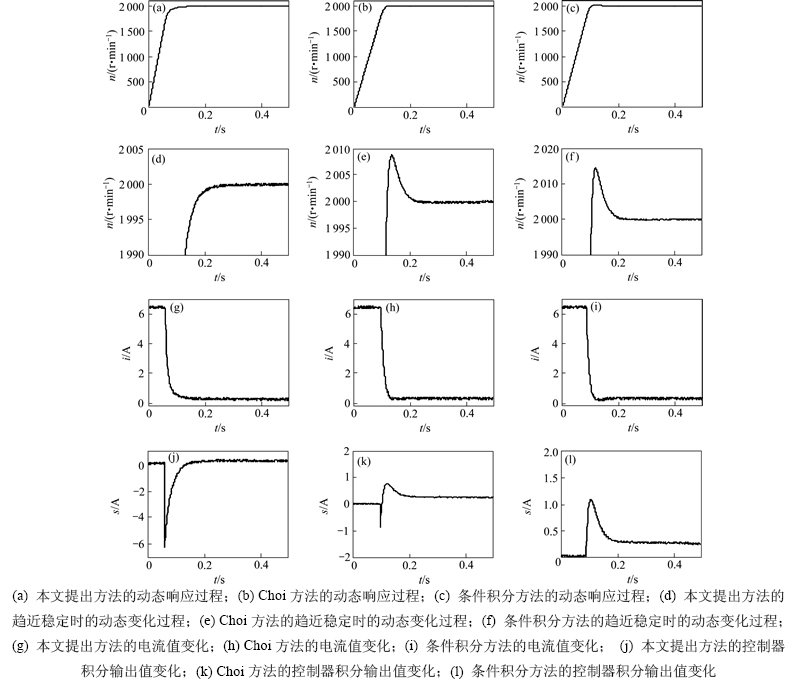
图5 永磁同步电机不同抗饱和方法的速度响应实验结果
Fig. 5 Experimental results of PMSM for speed responses with different anti-windup methods
2) Choi的方法采用了零极点相消的方法，从仿真和实验的稳态动态曲线上来看，Choi的曲线有更加急促的变化趋势，而在高速运行时容易对电机造成冲击，事实上本系统的2个极点为-34.77和-217.05，由控制理论可知主导极点为-34.77，存在零点和主导极点对消的情况，一方面系统的动态性能将失去设计的动态性能，另一方面极点-217.05决定了系统的动态收敛速度很快，容易造成对系统的冲击。同时，Choi的方法改变了系统的固有频率，有可能导致系统的共振。而本文提出的方法，保留了系统的极点特性，仿真和实验结果均平稳运行，很好地解决了由于噪声和模型的不确定性导致的系统超调运行、动态性能偏离设计期望及可能产生的共振问题。
4 结论
1) 提出了一种新颖的AW算法。该方法建立了基于非线性摩擦力的补偿和干扰抑制的模型，有效地抑制了模型的不确定性。
2) 根据误差时域响应函数推导出了系统无超调运行的条件。当系统运行在饱和状态且满足上述条件时，系统由P模式进入PI模式，并赋予积分初始值，该方法确保了退饱和系统的优良的动态性能和无超调运行。与其他方法相比，仿真和实验结果验证了该新型AW 设计的可行性及优越性。
参考文献：
[1] 盛义发, 喻寿益, 桂卫华, 等. 轨道车辆用永磁同步电机系统效率优化智能集成控制研究[J]. 中南大学学报(自然科学版), 2010, 41(6): 2252-2257.
CHENG Yifa, YU Shouyi, GUI Weihua, et al. Efficiency optimization of permanent magnet synchronous motor for rail vehicles based on intelligent integrated control[J]. Journal of Central South University (Science and Technology), 2010, 41(6): 2252-2257.
[2] Kothare M V, Campo P J, Morari M, et al. A unified framework for the study of antiwindup designs[J]. Automatica, 1994, 30(12): 1869-1883.
[3] Tarbouriech S, Turner M. Anti-windup design: An overview of some recent advances and open problems[J]. Control Theory & Applications, 2009, 3(1): 1-19.
[4] 杨明, 徐殿国, 贵献国. 永磁交流速度伺服系统抗饱和设计研究[J]. 中国电机工程学报, 2007, 27(15): 28-32.
YANG Ming, XU Dianguo, GUI Xianguo. Study of AC PMSM speed servo system anti-windup design[J]. Proceedings of the Chinese Society for Electrical Engineering, 2007, 27(15): 28-32.
[5] Peng Y B, Vrancic D, Hanus R. A Anti-windup, bumpless, and conditioned transfer techniques for PID controllers[J]. IEEE Control Systems, 1996, 16(4): 48-57.
[6] Walgama K S, Ronnback S, Sternby J. Generalisation of conditioning technique for anti-windup compensators[J]. IEE Proceedings Control Theory and Applications, 1992, 139(2): 109-118.
[7] Hodel A S, Hall C E. Variable-structure PID control to prevent integrator windup[J]. IEEE Transactions on Industrial Electronics, 2001, 48(2): 442-451.
[8] Bohn C, Atherton D P. An analysis package comparing PID anti-windup strategies[J]. IEEE Control Systems, 1995, 15(2): 34-40.
[9] Choi J W, Lee S C. Antiwindup strategy for PI-type speed controller[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 2039-2046.
[10] Hwi B S, Jong G P. Anti-windup PID controller with integral state predictor for variable-speed motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1509-1516.
[11] Chaoui H, Sicard P. Adaptive fuzzy logic control of permanent magnet synchronous machines with nonlinear friction[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1123-1133.
[12] 王瑞娟, 梅志千, 李向国, 等. 机电伺服系统非线性摩擦自适应补偿的研究[J]. 中国电机工程学报, 2012, 32(36): 123-129.
WANG Ruijuan, MEI Zhiqian, LI Xiangguo, et al. Research on adaptive nonlinear friction compensation of mechatronic servo systems[J]. Proceedings of the Chinese Society for Electrical Engineering, 2012, 32(36): 123-129.
[13] Bong K K, Wan K C. Advanced disturbance observer design for mechanical positioning systems[J]. IEEE Transactions on Industrial Electronics, 2003, 50(6): 1207-1216.
[14] Schrijver E, Van Dijk J. Disturbance observers for rigid mechanical systems: Equivalence, stability, and design[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(4): 539-548.
[15] 秦晓飞, 王云宽, 郑军, 等. 交流伺服系统振动鲁棒M/T测速算法[J]. 电机与控制学报, 2010, 14(5): 97-103.
QIN Xiaofei, WANG Yunkuan, ZHENG Jun, et al. Mechanical vibration-robust M/T speed detection method of AC servo system[J]. Electric Machines and Control, 2010, 14(5): 97-103.
(编辑 罗金花)
收稿日期：2014-01-23；修回日期：2014-03-30
基金项目(Foundation item)：国家科技重大专项(2013ZX04007-011)；“十一五”数控重大专项(2009ZX04010-023)；福建省科技重大专项(2012HZ0006-4) (Project(2013ZX04007-011) supported by the National Science and Technology Major Program of China; Project (2009ZX04010-023) supported by the Numerical Control Major Project during the 11th Five-year Plan Period；Project(2012HZ0006-4) supported by the Science and Technology Major Program of Fujian Province)
通信作者：秦晓飞，副研究员，从事电机驱动关键技术研究；E-mail: xiaofei.qin@ia.ac.cn
