J. Cent. South Univ. (2018) 25: 1938-1947

DOI: https://doi.org/10.1007/s11771-018-3884-7

Intraretinal layer segmentation and parameter measurement in optic nerve head region through energy function of spatial-gradient continuity constraint

CHEN Zai-liang(陈再良)^{1, 2}, WEI Hao(魏浩)^{1, 2}, SHEN Hai-lan(沈海澜)¹, PENG Peng(彭鹏)^{1, 2},YUE Ke-juan(岳珂娟)¹, LI Jian-feng(李建锋)³, ZOU Bei-ji(邹北骥)^{1, 2}

1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. Joint Laboratory of Mobile Health, Ministry of Education and China Mobile, Changsha 410083, China;

3. School of Information Science and Engineering, Jishou University, Jishou 416000, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: For the diagnosis of glaucoma, optical coherence tomography (OCT) is a noninvasive imaging technique for the assessment of retinal layers. To accurately segment intraretinal layers in an optic nerve head (ONH) region, we proposed an automatic method for the segmentation of three intraretinal layers in eye OCT scans centered on ONH. The internal limiting membrane, inner segment and outer segment, Bruch’s membrane surfaces under vascular shadows, and interaction of multiple high-reflectivity regions in the OCT image can be accurately segmented through this method. Then, we constructed a novel spatial-gradient continuity constraint, termed spatial-gradient continuity constraint, for the correction of discontinuity between adjacent image segmentation results. In our experiment, we randomly selected 20 B-scans, each annotated three retinal layers by experts. Signed distance errors of -0.80 μm obtained through this method are lower than those obtained through the state-of-art method (-1.43 μm). Meanwhile, the segmentation results can be used as bases for the diagnosis of glaucoma.

Key words: surface segmentation; parameter measurement; optical coherence tomography; optic nerve head; spatial-gradient continuity constraints

Cite this article as: CHEN Zai-liang, WEI Hao, SHEN Hai-lan, PENG Peng, YUE Ke-juan, LI Jian-feng, ZOU Bei-ji. Intraretinal layer segmentation and parameter measurement in optic nerve head region through energy function of spatial-gradient continuity constraint [J]. Journal of Central South University, 2018, 25(8): 1938–1947. DOI: https://doi.org/10.1007/s11771-018-3884-7.

1 Introduction

Special domain optical coherence tomography (SD-OCT) is a noninvasive imaging technique through which abundant structural information for biological tissues can be obtained [1, 2]. In ophthalmology, such information can be used for ophthalmologists in diagnosing some eye diseases that affect retinal structure, particularly age-related macular degeneration, diabetic macular edema, and pigment epithelial detachments. However, the retinal structures in patients with glaucoma have no abnormal changes. Thus, using optical coherence tomography (OCT) images for the diagnosis of glaucoma is ineffective. Fortunately, some structural parameters, such as retinal nerve fiber layer (RNFL) thickness, cup area/disc area ratio (CDR), and cup volume, in patients with glaucoma, are different from those of normal people [3, 4].These features can be computed from the OCT images although the computations require the segmentation of intraretinal layers. Thus, considering the large population base, condition of the aging population, and unbalanced proportion of doctors and patients, this method is time-consuming or even impossible to conduct because each retinal layer is segmented manually. Therefore, a method that enables the accurate and efficient computation of these parameters from OCT images is urgent and significant.

However, the segmentation of intraretinal layer in optical nerve head (ONH) region is challenging. On one hand, an OCT system is based on the interference of coherent optical beams, and OCT images have much speckle noise owing to the scattering effect of biomedical tissues [5, 6]. Speckle noise reduces the quality of OCT images and causes difficulties in segmenting the intraretinal layer. On the other hand, blood vessels in the ONH regions result in several vascular shadows in OCT images. These shadows cause the discontinuity of intraretinal layers, thereby affecting segmentation accuracy.

In recent years, many different algorithms have been proposed for these problems.

1) Influence of low contrast or speckle noise. For the segmentation of different intraretinal layers in OCT images, some segmentation methods based on the variations in the intensities in OCT image A-scans (column of an image) were proposed in early studies [7, 8]. In each A-scan, the pixel, of which intensity reaches a default threshold, is labeled as one point of an intraretinal layer boundary. Unfortunately, these methods are sensitive to vascular shadows and speckle noise. For these issues, LU et al [9] proposed an iterative polynomial smoothing method wherein the retinal blood vessel shadows in OCT images are detected and removed accurately. This method is based on the observation that vessel sections are usually much darker than nonvessel sections. In other studies, a fully automated segmentation algorithm, termed as FloatingCanvas, was used for the segmentation of intraretinal layers in 3D-OCT images [10]. The segmented results are analyzed for some key parameters, such as the location of blood vessels and RNFL thickness. Although this method is sensitive to variations in intensity, it is minimally affected by speckle noise. Overall, these methods enable the accurate segmentation of intraretinal layers in most instances, but they are sensitive to the low contrast between two adjacent layers or speckle noises in images.

2) Interference of vascular shadows. Some algorithms based on graph theory were implemented for the reduction of sensitivity of these methods to intensity variations. For instance, ANTONY et al [11] presented an automated 3D graph-search method for the segmentation of seven intraretinal surfaces in ONH-centered OCT images. Through this method, multiple surfaces can be detected simultaneously through the detection of a minimum-cost closed set in a vertex-weighted graph constructed by OCT images, and the border segmentation error is usually (7.25±1.08) μm. SHAH et al [12] employed an automated method for the segmentation of internal limiting membrane (ILM) surface based on the range expansion algorithm. In this method, the unsigned mean surface positioning error of the segmentation result is usually (6.35±1.35) μm, which is lower in other methods (7.69±3.23). LEE et al [13] proposed a multiscale 3D graph method for the segmentation of intraretinal layers in OCT images centered on the ONH region. The basic idea of the method is to determine the intraretinal surface in the high resolution image on the basis of segmentation results at a low resolution. Meanwhile, another method based on gradient vector flow and graph theory was proposed for the segmentation of an ILM surface within an ONH-centered spectral-domain OCT [14]. Through this method, the accurate detection of the position of a vascular shadow and measurement of cup volume parameter can be performed simultaneously. Nevertheless, these methods are affected by vascular shadows in OCT images, specifically those in the ONH region.

Considering the deficiencies of these methods and the challenges of intraretinal layer segmentation, we proposed an automatic method based on a new constraint function termed spatial-gradient continuity constraint (SGCC) for the segmentation of intraretinal layers in OCT images centered on ONH region. The contribution of this study is twofold as follows:

1) A Chan–Vese-Fuzzy C-Means (CV-FCM) method wherein fuzzy c-means clustering (FCM) [15] algorithm is combined with Chan–Vese (C–V) [16] algorithm is proposed. Through this method, the segmentation errors of the C–V algorithm are reduced, particularly those caused by the improper selection of an initial segmentation region.

2) A SGCC function is proposed, which combines the positional and gradient relationship between adjacent multiple images. The purpose of the SGCC function is to correct the segmentation errors resulting from insufficient relevant information between adjacent images.

2 Methods

The block diagram of the proposed method is shown in Figure 1. In the preprocessing step, block matching and 3D filtering (BM3D) [17] algorithm was used for the reduction of speckle noise in the SD-OCT images centered-on ONH. The CV-FCM method was used for the separation of multiple high-reflectivity regions in an OCT image. To locate the vascular shadows, we first constructed an OCT projection image by averaging the denoised images in z-direction. Then, the projection image was processed by a retinal vessel segmentation algorithm [18] for the generation of a vascular shadow location map (Section 2.2), which would be used as auxiliary information for intraretinal layer segmentation (Section 2.3). In Section 2.3, we employed the A-scan segmentation algorithm to obtain preliminary segmentation results and then we combined the vascular shadow location map with the proposed SGCC function to obtain the final segmentation results. Finally, the segmentation results were utilized for the computation of the parameters of retinal structure, such as cup area, disc area, and CDR.

2.1 Preprocessing

A high level of speckle noise was introduced during the OCT image generation. For the reduction of the speckle noise and preservation of edge information in the OCT image, the BM3D algorithm was adopted.Great similarity was observed between the intensities and between the edge gradients of these regions because the RNFL and retinal pigment epithelium (RPE) layer were both high-reflectivity regions. This similarity led to an inaccurate segmentation result. To reduce the influence of this similarity, we proposed a method for the separation of two high-reflectivity regions. The method was a combination of FCM and C–V algorithm and termed CV-FCM. Two separated regions were used as regions of interest (ROI) in the intraretinal layer segmentation step (Section 2.3).

FCM algorithm, a fuzzy clustering algorithm based on pixel intensity similarity, clusters the pixel with similar intensity to one class to segment image into foreground and background. FCM was used to segment the image I into c classes C={μ₁, …, μ_c}:

(1)

where J is the objection function of FCM; U represents the partition matrix of size H×W×c, in which the function means the probability of pixel (i, j) belonging to the class k; m is the index coefficient. In addition, μ_k, the kth cluster center, is updated as the average intensity of current category in each iteration, and 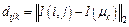represents the norm of the intensity differences between point (i, j) and point μ_k.

After minimizing the object function J, c images corresponding to c classes were obtained. To obtain the image, which contains the retinal region only, we computed the summation of intensity in each image and then selected the image, which corresponds to the minimum summation as clustering result M.

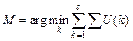                     (2)

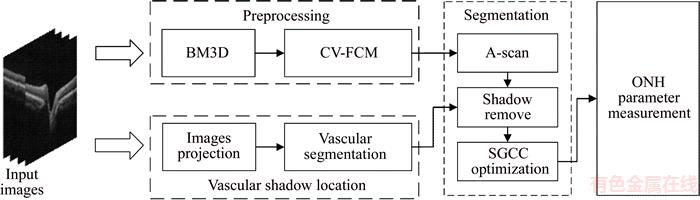
Figure 1 Block diagram of proposed method

where U(k) indicates the image, which corresponds the class k; 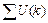represents the summation of intensity in this image.

Considering that the boundary of the retinal region is not smooth in M, we used M as initial segmentation region of C–V algorithm [14], a region-based active contour model. In the image segmentation, pixel intensity was used to construct the energy function of C–V algorithm.

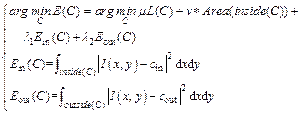(3)

where I is the image processed by BM3D algorithm; C represents the contour curve of the retinal area from M; L(C) means the length of C; μ, v, λ₁, λ₂ are constant parameters, which can be adjusted. The default value of v is zero. Moreover, inside(C) and outside(C) represent the region inside and outside the contour C, respectively. The variables c_in and c_out are the average intensities of inside(C) and outside(C), respectively. The final result after the minimization of the energy function E(C) contains two high-reflectivity regions, namely, RNFL and RPE. The two regions were then separated according to their relative position relationship. Two separated regions were used as ROI in intraretinal layer segmentation step (Section 2.3).

2.2 Vascular shadow location

The images of each eye were obtained by performing a 128-line scan mode on the retina ONH region. Thus, the intersection position of the fundus vascular network and scanning line is consistent with the position of the vascular shadow in the corresponding OCT image. To acquire the position of vascular shadow, we generated a projection image by averaging the denoised images in the z-direction. Then, a blood vessel network was segmented. The blood vessel network segmentation method based on Gaussian filter strategy and Otsu algorithm was adopted [18, 19]. Figure 2 shows the process of this step.

The inverse process shown in Figure 2 was utilized for the location of vascular shadows in the OCT image. The location information improves the accuracy of surface segmentation in Section 2.3.

2.3 Intraretinal surface segmentation

In this section, we combined the ROI from Section 2.1 and the location of vascular shadow from Section 2.2 to segment ILM, inner segment and outer segment (IS-OS), and Bruch’s membrane (BM) surface.

Considering the segmentation errors caused by the lack of relevance information between the adjacent images [7], we proposed a spatial-gradient continuity constraint function, termed SGCC, for the restraint of segmentation result in order to obtain a good segmentation result.

First, we performed the A-scan algorithm to obtain a preliminary result. The A-scan algorithm is described as follows:

       (4)

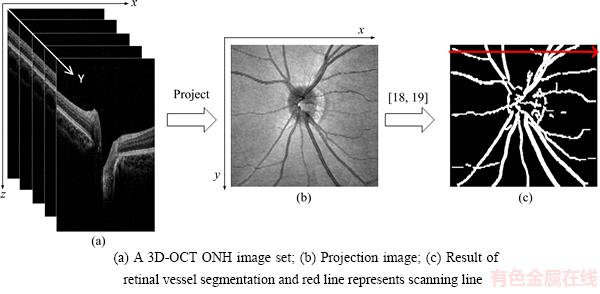
Figure 2 Process of vascular shadow positioning:

where Can(j) represents the index of the pixel in the image jth column that maximizes the objective function, and 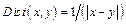indicates the reciprocal of the differences between the index of two adjacent segmented points. ROI(i, j) indicates the intensity of image, which contains separated high-reflectivity region in Section 2.2. In addition, α and γ are the coefficients of grayscale term and distance term, respectively. In this study, we set the value of α and γ at 0.6 and 0.4, respectively. By solving Eq.(4), we can acquire the segmented results.

Some errors in the segmentation result were observed due to the presence of vascular shadows, as shown in Figure 3. Consequently, the segmented points located in the shadow region were removed based on the vascular shadow location, and then polynomial curve fitting was used to make up removed points, as shown in Figure 3(c).

After finishing the correction of segmentation errors caused by the vascular shadows, the condition that multi-adjacent points showed continuous segmentation errors happens simultaneously. To prevent this result, we proposed an SGCC function based on the positional relationship of multi-adjacent images and similarity among the gradients of adjacent points.

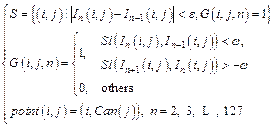  (5)

where I_n(i, j) represents the point (i, j) in the nth image, and Sl(x, y) indicates the slope between point x and y. The point in the set Can, which meets the conditions, is selected into the set S. In addition, ε>0 and ω>0 indicate the thresholds of Euclidean distance and gradient between two adjacent segmented points, respectively. The segmented point will be removed if the distance is greater than the threshold. Finally, S is set of final segmented points.

2.4 ONH parameter measurement

LI et al [20] found that some structural parameters (cup area, cup volume, and CDR) in the ONH region of normal patients are remarkably different from those of patients with glaucoma.Thus, these parameters in ONH region were mainly measured in this study.

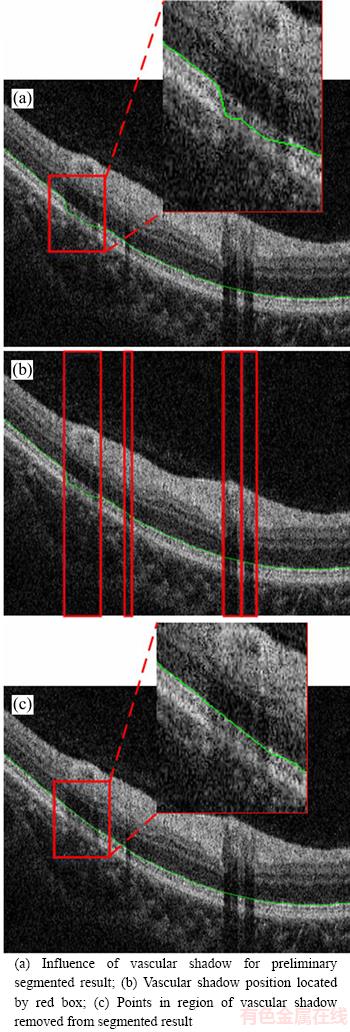
Figure 3 Process of removing vascular shadows:

For a single image, the “reference surface” is defined by connecting two Bruch membrane opening (BMO) points also named as RPE end point, as shown in Figure 4. Then, we moved the “reference surface” vertically by a given distance (150 μm [14]) and obtained two crossing points with ILM (yellow points in Figure 4). This crossing point is the cup detection point, which is defined as the projection of an optical cup edge in the OCT image. The area enclosed by moved “reference surface” (yellow line in Figure 4) and ILM is defined as the cup area. The disc area is defined in the same manner.

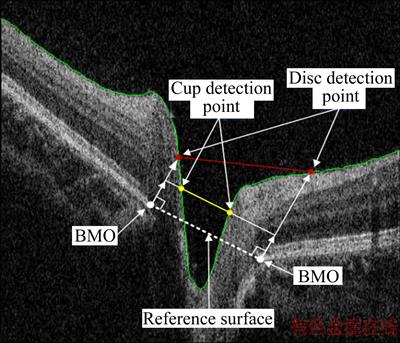
Figure 4 Illustration of locating cup and disc point (The red and yellow lines are the upper bound of disc area and cup area, respectively. The white dotted line is the reference surface, and the green line represents the ILM boundary. The vertical distance between white dotted and yellow line is 150 μm)

3 Experiments and results

To evaluate the performance of the proposed method from OCT retinal images, we collected 3D-OCT images sets centered on ONH region. A Topcon 3D OCT-1 Maestro system was used in this step. The resolution of each image set is 6 mm×6 mm×2 mm corresponding to 512×128×885 voxels. To compare the proposed method with the ground truth, we randomly selected 20 spectral-domain OCT B-scans, each with three retinal layers annotated by experts, from these image sets.

Figure 5 shows the examples of the segmentation results, wherein surface 1 is ILM, surface 2 is IS-OS, and surface 3 is BM. Figure 5(b) shows the 52th B-scan, wherein the segmentation results of the proposed method are extremely close to the ground truth. The yellow line in Figure 5(b) is the perpendicular of BMO point, and the region between the two lines is the neural canal region. To view the shape of intraretinal layer, we illustrated three segmented surfaces in a 3D schema in Figure 6. Figure 7 indicates the segmentation results of six samples. As indicated by these results, three intraretinal surfaces in the OCT images centered on the ONH region were accurately segmented through the proposed method.

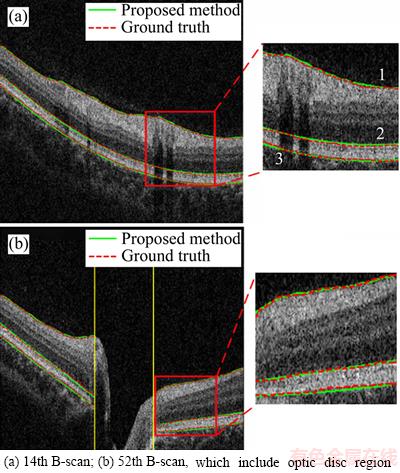
Figure 5 Segmentation results of three intraretinal surfaces of two B-scans:(Surface 1: Internal limiting membrane (ILM); surface 2: the boundary between inner segment (IS) and outer segment (OS); surface 3: the boundary between retinal pigment epithelium (RPE) and choroids)

The signed and unsigned mean errors and standard deviations (SDs) between the segmentation results and ground truth are shown in Table 1. Among the surfaces, the first surface has the best performance, having signed and unsigned errors of -1.52±3.70 and 3.36±2.47, respectively. The third surface (BM) shows the worst result. The true BM surface is blurred because biological tissue reflectivity is not uniform in the region between the RPE layer and choroid. The performance of our proposed method for ILM surface segmentation was compared with other algorithms (Table 2). The proposed method has smaller signed and unsigned mean differences than those of LEE et al [13] and MIRI et al [14] but has larger SD difference than that of [14]. These errors result from the extremely steep boundary in the neural canal region.The presence of this boundary leads to large segmentation and vertical errors.

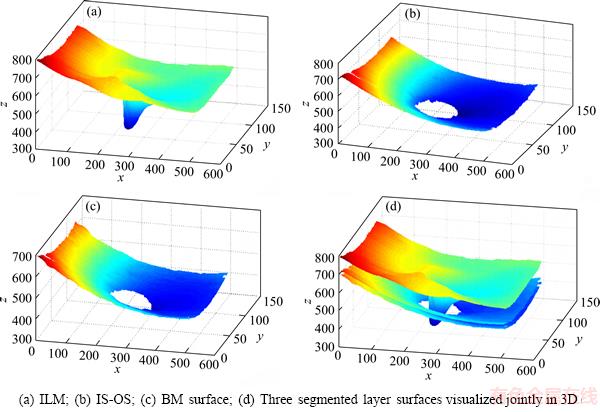
Figure 6 3D reconstruction of segmented surfaces: (The shape of the segmented surface is related to some eye diseases)

Bland–Altman (B&A) analysis can be used for the evaluation of the agreement between two different methods. If the agreement meets the prescribed conditions, the two methods can be used interchangeably. In this study, we evaluated the agreement between the proposed method and the expert segmentation by the B&A analysis. The analysis result is shown in Figure 8, where the y axis represents the difference between the two methods, whereas the x axis represents the average of the results of the two methods. B&A recommends that 95% of the data points should lie within ±1.96SD of the mean difference. After experimental analysis, 96.2%, 94.7% and 99.7% points are observed within ±1.96SD. Therefore,the agreement among the proposed method and expert segmentation is high, and the proposed method can largely replace expert manual segmentation.

Table 3 shows the parameters of ONH region measured from an experimental image, where the CDR is the ratio of cup area and disc area. Given the discontinuity between the OCT images in the y axis, errors exist between the measured and actual parameters.

4 Conclusions

1) This study proposed an automated intraretinal layer segmentation method based on the SGCC function for OCT images centered on the ONH region. The structural parameters in the ONH region, including cup area, cup volume, and CDR, were measured through this method. The experimental results suggest that the proposed method is robust to speckle noises and vascular shadows. The average signed and unsigned errors of the three surface segmentation results are (2.62±5.66) and (5.71±4.33) μm, respectively, and the best results ((-1.52±3.70) and (3.36±2.47) μm) are obtained through ILM surface segmentation.

2) The measurement of structural parameters relies on the positions of BMO. The corresponding relationship between the projection image and the 3D OCT images indicates that the optic disc boundary in the projection image and the BMO points of the OCT images has a one-to-one correspondence. In this study, the optic disc boundary was manually segmented by experts. Therefore, one future research direction is the segmentation of BMO point from 3D OCT images.Meanwhile, RNFL thickness in the ONH region, which is better parameter than ONH parameters for glaucoma discrimination, was not measured in this work. Thus, we are currently working toward the extension of the proposed method for the measurement of RNFL thickness.

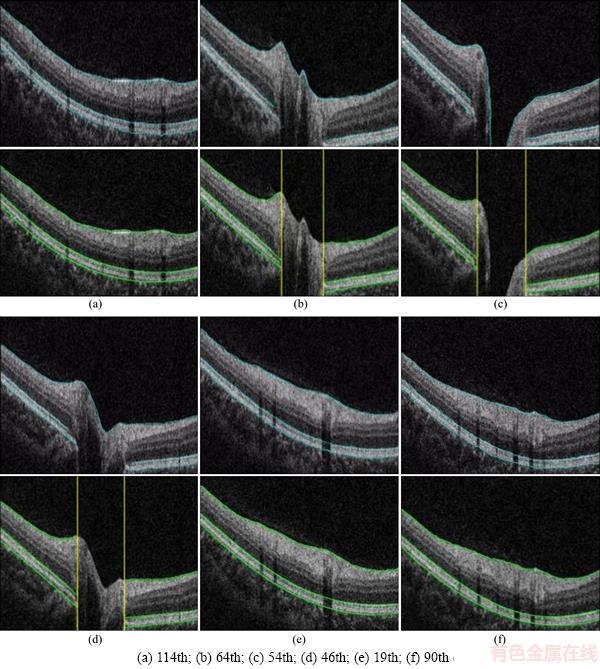
Figure 7 Segmentation result of six B-scans:(For each B-scan, top row is the ground truth, and bottom row is the proposed method segmentation results)

Table 1 Three surface segmentation results of proposed method

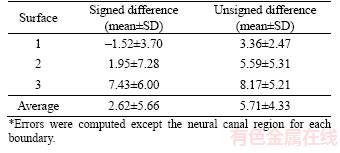
Table 2 Average signed and unsigned border positioning errors (mean±SD) for ILM segmentation

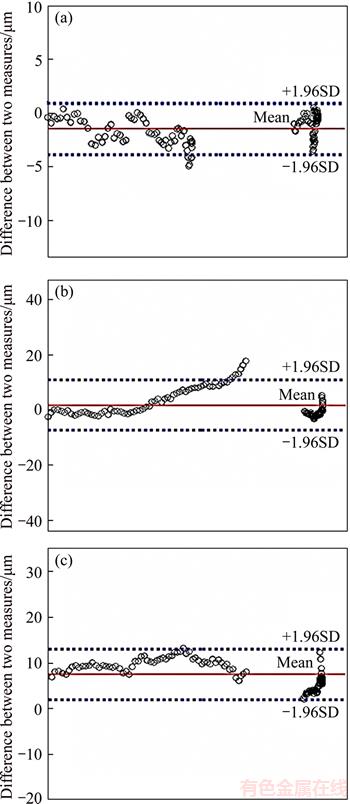
Figure 8 Bland–Altman graphs of surface segmentation result corresponding to ground truth vs proposed method for ILM (a), IS-OS (b), and BM (c), respectively (differences for each boundary was computed except the neural canal)

Table 3 Parameter measurement of ONH region

References

[1] HUANG D, SWANSON E A, LIN C P, SCHUMAN J S, STINSON W G, CHANG W. Optical coherence tomography [J]. Science, 1991, 254(5035): 1178–1181.

[2] DREXLER W, FUJIMOTO J G. Optical coherence tomography: Technology and applications [M]. Berlin: Springer, 2015.

[3] GARAS A, VARGHA P, HOLLO G. Diagnostic accuracy of nerve fibre layer, macular thickness and optic disc measurements made with the RTVue-100 optical coherence tomograph to detect glaucoma [J]. Eye, 2011, 25(1): 57–65.

[4] MWANZA J C, OAKLEY J D, BUDENZ D L, ANDERSON D R. Ability of cirrus HD-OCT optic nerve head parameters to discriminate normal from glaucomatous eyes [J]. Ophthalmology, 2011, 118(2): 241–248.

[5] SCHMITT J M, XIANG S H, YUNG K M. Speckle in optical coherence tomography [J]. Journal of Biomedical Optics, 1999, 4(1): 95–106.

[6] CURATOLO A, KENNEDY B F, SAMPSON D D, HILLMAN T R. Speckle in optical coherence tomography [M]. London: Taylor & Francis, 2013.

[7] ISHIKAWA H, STEIN D M, WOLLSTEIN G, BEATON S, FUJIMOTO J G, SCHUMAN J S. Macular segmentation with optical coherence tomography [J]. Investigative Ophthalmology & Visual science, 2005, 46(6): 2012–2017.

[8] AHLERS C, SIMADER C, GEITZENAUER W, STOCK G, STETSON P, DASTMALCHI S, SCHMIDT-ERFURTH U. Automatic segmentation in three-dimensional analysis of fibrovascular pigmentepithelial detachment using high- definition optical coherence tomography [J]. British Journal of Ophthalmology, 2008, 92(2): 197–203.

[9] LU Shi-jian, CHEUNG C Y, LIU Jiang, LIM J H, WONG T Y. Automated layer segmentation of optical coherence tomography images [J]. IEEE Transactions on Biomedical Engineering, 2010, 57(10): 2605–2608.

[10] ZHU Hao-gang, CRABB D P, SCHLOTTMANN P G, HO T, GARWAY-HEATH D F. FloatingCanvas: Quantification of 3D retinal structures from spectral-domain optical coherence tomo-graphy [J]. Optics Express, 2010, 18(24): 24595–24610.

[11] ANTONY B J, ABRMOFF M D, LEE K, SONKOVA P, GUPTA, P, KWON Y, GARVIN M K. Automated 3D segmentation of intraretinal layers from optic nerve head optical coherence tomography images [C]// WEVER J B, MOLTHEN R C. Medical Imaging 2010: Biomedical Applications in Molecular, Structural, and Functional Imaging. California: International Society for Optics and Photonics, 2010: 76260U.

[12] SHAH A, WANG J K, GARVIN M K, SONKA M, WU Xiao-dong. Automated surface segmentation of internal limiting membrane in spectral-domain optical coherence tomography volumes with a deep cup using a 3-D range expansion approach [C]// 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI). IEEE, 2014: 1405–1408.

[13] LEE K, NIEMEIJER M, GARVIN M K, KWON Y H, SONKA M, ABRAMOFF M D. Segmentation of the optic disc in 3-D OCT scans of the optic nerve head [J]. IEEE Transactions on Medical Imaging, 2010, 29(1): 159–168.

[14] MIRI M S, ROBLES V A, ABRMOFF M D, KWON Y H, GARVIN M K. Incorporation of gradient vector flow field in a multimodal graph-theoretic approach for segmenting the internal limiting membrane from glaucomatous optic nerve head-centered SD-OCT volumes [J]. Computerized Medical Imaging and Graphics, 2017, 55: 87–94.

[15] BEZDEK J C, EHRLICH R, FULL W. FCM: The fuzzy c-means clustering algorithm [J]. Computers & Geosciences, 1984, 10(2, 3): 191–203.

[16] CHAN T F, VESE L A. Active contours without edges [J]. IEEE Transactions on Image Processing, 2001, 10(2): 266–277.

[17] DABOV K, FOI A, KATKOVNIK V, EGIAZARIAN, K. Image denoising by sparse 3-D transform-domain collaborative filtering [J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080–2095.

[18] LIU Qing, ZOU Bei-ji, CHEN Jie, KE Wei, YUE Ke-juan, CHEN Zai-liang, ZHAO Guo-ying. A location-to- segmentation strategy for automatic exudate segmentation in colour retinal fundus images [J]. Computerized Medical Imaging and Graphics, 2017, 55: 78–86.

[19] YAO Chang, CHEN Hou-jin. Automated retinal blood vessels segmentation based on simplified PCNN and fast 2D-Otsu algorithm [J]. Journal of Central South University of Technology, 2009, 16(4): 640–646.

[20] LI Song-feng, WANG Xiao-zhen, LI Shu-ning, WU Ge-wei, WANG Ning-li. Evaluation of optic nerve head and retinal nerve fiber layer in early and advance glaucoma using frequency-domain optical coherence tomography [J]. Graefe’s Archive for Clinical and Experimental Ophthalmology, 2010, 248(3): 429–434.

[21] SUNG K R, NA J H, LEE Y. Glaucoma diagnostic capabilities of optic nerve head parameters as determined by Cirrus HD optical coherence tomography [J]. Journal of Glaucoma, 2012, 21(7): 498–504.

(Edited by YANG Hua)

中文导读

基于空间连续性约束的视乳头区域视网膜内层次分割与参数测量

摘要：光学相干断层扫描（OCT）是一种无创的成像技术，通常通过评估视网膜层的形态结构来诊断青光眼。为了准确分割视乳头（ONH）区域OCT图像中的视网膜内层次，提出一种自动分割视网膜内层次的方法。该方法能够在血管阴影、多个高反射区相互影响的情况下分割出ILM、IS-OS和BM。然后，构造出一种新的能量约束条件，称为空间连续性约束，用于修正相邻图像之间分割结果的不连续性。在实验中，随机选择20张图像，其中每张图像含有3条专家标定的分割线。相比较于目前最好算法–1.43 μm的Signed误差，我们提出的方法获得了–0.80 μm的Signed误差。同时，该分割结果能够为青光眼的诊断过程提供辅助信息。

关键词：层次分割；参数测量；光学相干断层扫描；视乳头；空间连续性约束

Foundation item: Projects(61672542, 61573380) supported by the National Natural Science Foundation of China

Received date: 2017-05-21; Accepted date: 2017-12-19

Corresponding author: SHEN Hai-lan, PhD, Associate Professor; Tel: +86–13667348102; E-mail: hn_shl@126.com; ORCID: 0000- 0002-8558-1443