J. Cent. South Univ. Technol. (2011) 18: 1602-1608
DOI: 10.1007/s11771-011-0878-0
Similarity measure design and similarity computation for discrete fuzzy data
LEE Sang-Hyuk1, PARK Wook-Je2, JUNG Dong-yean3
1. Department of Electrical and Electronic Engineering, Xi’an Jiaotong-Liverpool University, Suzhou 215123, China;
2. Institute for Information and Electronics Research, Inha University, 253 Yonghyun-dong,Nam-Gu, Incheon, 402-751, Korea;
3. Daeho Technology Korea Co., Ltd, Changwon, Gyeongnam, 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: The similarity computations for fuzzy membership function pairs were carried out. Fuzzy number related knowledge was introduced, and conventional similarity was compared with distance based similarity measure. The usefulness of the proposed similarity measure was verified. The results show that the proposed similarity measure could be applied to ordinary fuzzy membership functions, though it was not easy to design. Through conventional results on the calculation of similarity for fuzzy membership pair, fuzzy membership-crisp pair and crisp-crisp pair were carried out. The proposed distance based similarity measure represented rational performance with the heuristic point of view. Furthermore, troublesome in fuzzy number based similarity measure for abnormal universe of discourse case was discussed. Finally, the similarity measure computation for various membership function pairs was discussed with other conventional results.
Key words: similarity measure; fuzzy number; distance; similarity evaluation; fuzzy membership function
1 Introduction
Computation of similarity between two or more kinds of information was very interesting for the fields of decision making, pattern classification, and so on [1-3]. Until now the research of designing similarity measure has been carried out by numerous researchers [4-9]. Most studies were emphasized on designing similarity measure based on membership function or fuzzy number [5, 8]. Similarity measure design with fuzzy number was easier than with distance measure, however, similarity measure construction was possible only for triangular or trapezoidal fuzzy membership function [5-7]. Furthermore, it was also vague to obtain the degree of similarity between crisp sets or between crisp set and fuzzy set.
Mentioned similarity design with distance measure was proposed and proved. Additionally, comparison of similarity design with fuzzy number was carried out. Similarity computation between crisp data needed more consideration, because it was not reported by many researchers. Furthermore, previous results on similarity measure mainly treated on the data sets. Hence, to obtain the similarity measure application to the crisp data it has to be careful for applying similarity measure. Furthermore, it also could be applied to general fuzzy membership functions. In comparison example, similarity based on distance measure was applied to similarity evaluation of two fuzzy membership functions, and the result of the degree of similarity between fuzzy set and crisp set was analyzed. First, similarity measure which was derived from fuzzy number was introduced and discussed. Next, similarity based on distance measure was derived and explained through the concept of certainty and uncertainty. The larger the area of coinciding certainty is, the better the similarity grows. Two similarity measures that were derived from fuzzy number and distance measure were compared with the evaluation of fuzzy membership function pairs. Two similarity measures had their own advantages: fuzzy number methods was simple and easy to compute similarity if membership function is satisfied by trapezoidal or triangular type; whereas similarity based on distance method needed more time and consideration, however, it could be applied to the general membership function. At this point, it was interesting to study and compare the two similarity measures for the fuzzy set and crisp set.
In this work, preliminary results on fuzzy number, center of gravity, and the similarity measure were introduced. The similarity measures with distance measure and fuzzy number were derived and proved and two similarity measures computations were compared and discussed. Then, comments for the similarity with fuzzy number were carried out. Notations of Ref.[10] were used.
2 Similarity measure preliminaries
In order to understand the similarity measure design with fuzzy number, it is required to study fuzzy number, center of gravity, and axiomatic definitions of similarity measure. A generalized fuzzy number  is defined as
is defined as  =(a, b, c, d, w) where 0
=(a, b, c, d, w) where 0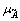 of fuzzy number
of fuzzy number  satisfys the following conditions [7]:
satisfys the following conditions [7]:
1) 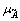 is a continuous mapping from real number R to the closed interval [0, 1];
is a continuous mapping from real number R to the closed interval [0, 1];
2) 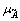 =0, when -∞
=0, when -∞
3) 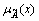 is strictly increasing on [a, b];
is strictly increasing on [a, b];
4) 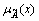 =w, when b≤x≤c;
=w, when b≤x≤c;
5) 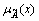 is strictly decreasing on [c, d];
is strictly decreasing on [c, d];
6) 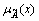 =0, when d≤x<∞.
=0, when d≤x<∞.
If b=c is satisfied, then it would be natural to satisfy triangular type. Four fuzzy number operations were also found in Ref.[7].
Traditional center of gravity (COG) is defined by
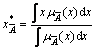
where 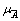 is the membership function of the fuzzy number
is the membership function of the fuzzy number 
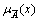 indicates the membership value of the element x in
indicates the membership value of the element x in  and generally,
and generally, 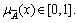 CHEN
CHEN
[4] presented a new method to calculate COG point of a generalized fuzzy number. They derived a new COG calculation method based on the concept of the medium curve. These COG points played an important role in the calculation of similarity measure with fuzzy number.
LIU [10] suggested axiomatic definition of similarity measure as follows. By this definition, numerous similarity measures could be derived.
Definition 1: A real function s: F2→R+ is called a similarity measure, if s has the following properties:
(S1) 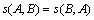 ,
,  ;
;
(S2) 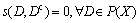 ;
;
(S3) 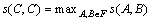 ,
, 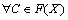 ;
;
(S4) 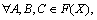 if
if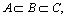 then s(A, B)≥ s(A, C) and s(B,C)≥s(A, C).
then s(A, B)≥ s(A, C) and s(B,C)≥s(A, C).
where R+=[0, ∞); X is the universal set; F(X) is the class of all fuzzy sets of X; P(X) is the class of all crisp sets of X; Dc is the complement of D. LIU [10] also pointed out that there was a one-to-one relation between all distance measures and all similarity measures, d+s=1. Fuzzy number similarity measure on F(X) was also obtained by the division of maximal value.
3 Similar measure by fuzzy number and distance measure
Now, similarity measure derivations with fuzzy number and distance measure are introduced. The first one is based on fuzzy number, and the second one is designed through distance measure, which are all contained in previous results [4-7]. However, evaluation in the similarity understand of back ground is needed.
3.1 Similarity measure via fuzzy number
In Refs.[4-7], degrees of similarities were derived through fuzzy number which was related with membership function and center of gravity. CHEN [4] introduced the degree of similarity for trapezoidal or triangular fuzzy membership function of  and
and  as follows:
as follows:
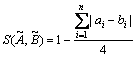 (1)
(1)
where  . If
. If  and
and 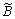 were triangular or trapezoidal fuzzy numbers, then n could be three or four. For trapezoidal membership function, fuzzy number satisfies
were triangular or trapezoidal fuzzy numbers, then n could be three or four. For trapezoidal membership function, fuzzy number satisfies  =(a1, a2, a3, 1) and
=(a1, a2, a3, 1) and 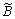 =(b1, b2, b3, 1).
=(b1, b2, b3, 1).
HSIEH et al [5] also proposed similarity measure for the trapezoidal and triangular fuzzy membership function as follows:
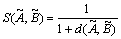 (2)
(2)
where 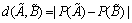 , and if
, and if  and
and 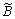 were triangular fuzzy numbers, then the graded mean integration of
were triangular fuzzy numbers, then the graded mean integration of  and
and 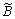 was defined as follows :
was defined as follows :
 and
and 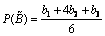
If  and
and 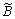 were trapezoidal fuzzy numbers, then the graded mean integration of
were trapezoidal fuzzy numbers, then the graded mean integration of  and
and 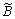 was also defined as follows:
was also defined as follows:
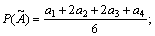
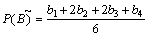
LEE [6] derived the trapezoidal similarity measure using fuzzy number operation and norm definition. That was
 (3)
(3)
where 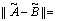
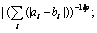 ||U||=max(U)-min(U)
||U||=max(U)-min(U)
and P is the natural number greater than or equals 1; U is the universe of discourse.
CHEN and CHEN [7] proposed a similarity measure to overcome the drawbacks of the existing similarity:
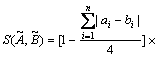
 (4)
(4)
where 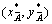 and
and 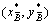 are the COGs of fuzzy number
are the COGs of fuzzy number  and
and 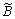 ;
; 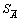 and
and 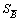 are expressed by
are expressed by 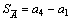 and
and 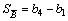 if they are trapezoidal.
if they are trapezoidal.  is denoted as one if
is denoted as one if 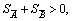 and zero if
and zero if 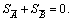 In Eq.(4),
In Eq.(4),  was used to determine whether COG distance was considered.
was used to determine whether COG distance was considered.
3.2 Similarity measure with distance function
To design the similarity measure via distance, it is needed to introduce the distance measure [10].
Definition 2: A real function d: F2→R+ is called a distance measure on F, if d satisfies the following properties:
(D1) 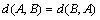 ,
, 
(D2) 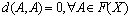
(D3)  ,
, 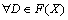
(D4) 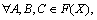 if
if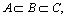 then d(A, B)≥ d(A, C) and d(B,C)≥d(A, C).
then d(A, B)≥ d(A, C) and d(B,C)≥d(A, C).
A real function s: F2→R+ is called a similarity measure, if s has the following properties:
(S1) 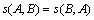 ,
, 
(S2) 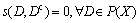
(S3) 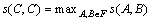 ,
, 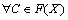
(S4) 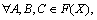 if
if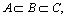 then s(A, B)≥ s(A, C) and s(B,C)≥s(A, C).
then s(A, B)≥ s(A, C) and s(B,C)≥s(A, C).
Hamming distance was commonly used as distance measure between fuzzy sets A and B:
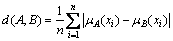
where X={x1, x2, …, xn}; μA(x) is the membership function of A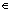 F(X); μB(x) is the membership function of B
F(X); μB(x) is the membership function of B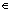 F(X). The following theorem satisfies similarity measure.
F(X). The following theorem satisfies similarity measure.
Theorem 1: For any set A, B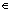 F(X), if d satisfies Hamming distance measure, then
F(X), if d satisfies Hamming distance measure, then
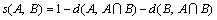 (5)
(5)
is the similarity measure between set A and set B.
Proof: Commutativity of (S1) is clear from Eq.(5) itself. To show the property of (S2),


was obtained because
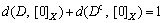 .
.
where [0]X and [1]X denote zero and one for the whole universe of discourse of X. Hence, (S2) is satisfied. (S3) is also easy to prove,
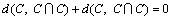 .
.
It is logical that s(C, C) satisfied maximal value. Finally, (S4) states
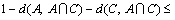
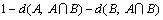
because
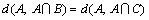 and
and
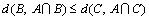
are satisfied. Similarly, s(B, C)≥s(A, C) is also satisfied.
The mentioned similarity is useful for the non interacting fuzzy membership function pair. Another similarity was also derived through distance measure.
Theorem 2: For any set A, B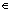 F(X), if d satisfies Hamming distance measure, then
F(X), if d satisfies Hamming distance measure, then
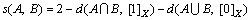 (6)
(6)
is also similarity measure.
With Eqs.(5) and (6), the evaluations of the degree of similarity between fuzzy sets are possible. Next, how to compute the degree of similarity between fuzzy set and crisp set is presented. In Fig.1, there are three membership function pairs. Naturally, three pairs must have different degree of similarity.
Now fuzzy set B in Eqs.(5) and (6) is replaced by crisp set Anear, where
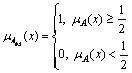
Anear is represented when Anear=A0.5, as shown in Fig.2, and rectangular shape of membership function of A reveals crisp set. If the width of rectangle became narrow, it could be represented by singleton in Fig.1. Furthermore, two times of difference area between two sets of Fig.2 represents the fuzzy entropy of fuzzy set A [11-13]. Two membership functions are identical, then entropy could be zero, which means that the degree of similarity becomes the maximum value.

Fig.1 Illustration of fuzzy data set and crisp data: (a) Non- overlap pair; (b) Partially overlapped pair; (c) Fully overlapped pair
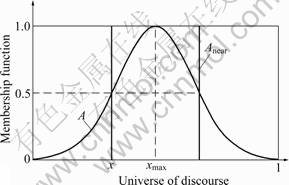
Fig.2 Membership function of fuzzy set A and crisp set Anear
Now, it is possible to represent the degree of similarity between fuzzy set and crisp set. Next theorem means the fuzzy set A similarity measure itself or the degree of similarity between fuzzy set A and crisp set Anear.
Theorem 3: For fuzzy set A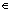 F(X) and Hamming distance measure d,
F(X) and Hamming distance measure d,
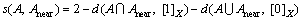 (7)
(7)
is the similarity measure of fuzzy set A and crisp set Anear.
Proof: Proofs can found in Ref.[9].
Similarly, Theorem 3 could be extended for the similarity measure between fuzzy set and crisp set in the next theorem.
Theorem 4: For any set A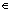 F(X), if d satisfies Hamming distance measure, then
F(X), if d satisfies Hamming distance measure, then
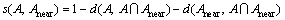 (8)
(8)
is the similarity measure of fuzzy set A and crisp set Anear.
4 Computation of similarity measure
CHEN and CHEN [7] computed the degree of similarity for 12 membership function sets. Twelve pairs contain fuzzy-fuzzy sets, crisp-crisp sets, and fuzzy-crisp sets. The considered examples are illustrated in Fig.3. There are two exact data pairs such as Set 2 and Set 6. Obviously, the similarity degree of these two data pair should be one. And the similarity of other ten data pairs should be placed in between zero to one.
They proposed seven descriptions compared to the existing method. One of the descriptions is represented as follows:
From Set 3, we can see that  and
and 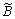 are different generalized fuzzy numbers.
are different generalized fuzzy numbers.
The other six descriptions also pointed out the same degree of similarity with other methods [7]. The main characteristics of CHEN and CHEN represented that ten sets were all different except Set 2 and Set 6. With similarity measure in Eq.(5), twelve sets similarity evaluation was carried out. From the computation, same results with those of CHEN and CHEN were obtained, i.e different similarity degrees between ten sets except Set 2 and Set 6. Similarity computation results are illustrated in Table 1.
With Eq.(4), CHEN and CHEN computed the similarity degree of Set 8 as follows:

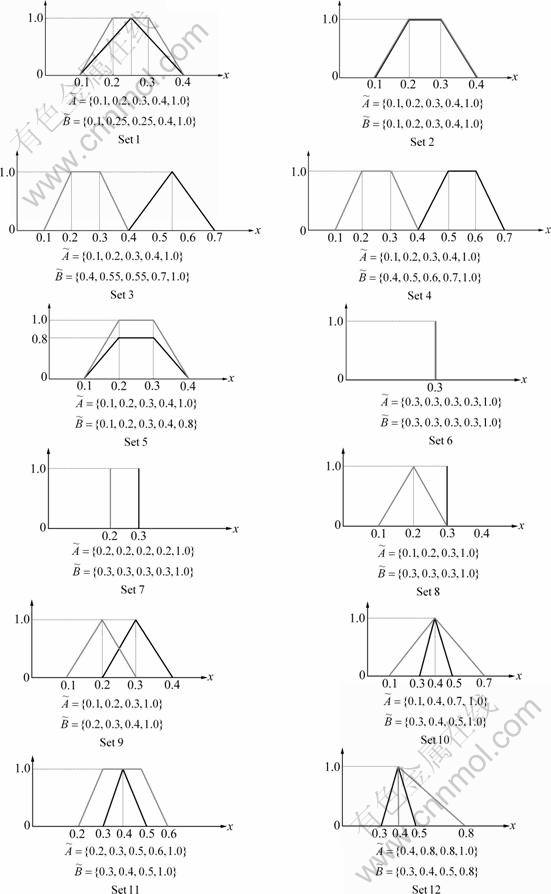
Fig.3 Twelve sets of data pairs of example of Ref.[7]
Table 1 Comparison of similarity degree for Fig.3 with conventional ones and proposed method
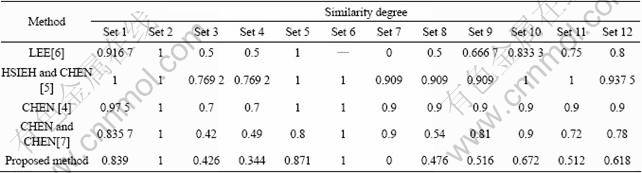
However, with similarity measure in Eq.(5), for fuzzy set A, the domain can be from 0.1 to 0.3 among universe of discourse, whereas crisp set B has only one when domain is 0.3. Consider the following computation conditions:
Universe of discourse: 0.1-0.8
Data points: 70
Sample distance: 0.01
Computation result shows that the similarity degree satisfies 0.476.
Finally, one more interesting comparison is the result of Set 7 similarity comparison. CHEN and CHEN computed as follows:

This computation was obtained from Eq.(4). However, there could be another way of approach to the similarity between crisp sets. With similarity measure Eq.(6) similarity computation of Set 7 pair was obtained by

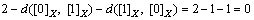
where 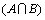 means the min(A(xi), B(xi)), hence it satisfies [0]X;
means the min(A(xi), B(xi)), hence it satisfies [0]X; 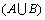 represents the maximum value between A(xi) and B(xi). By inspection of Set 7, two variables 0.2 and 0.3 have the corresponding membership value
represents the maximum value between A(xi) and B(xi). By inspection of Set 7, two variables 0.2 and 0.3 have the corresponding membership value 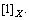 Therefore,
Therefore,
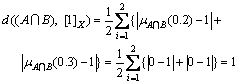
and
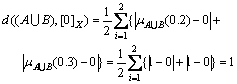
are satisfied.
For similarity with Eq.(4), to satisfy similarity measure zero, it has to be satisfied for
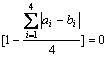 or
or 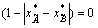 .
.
For this satisfaction, summation of all difference satisfied four for trapezoidal case, or the difference of x-COG also satisfied one.
Fuzzy membership function pairs of Fig.4 show the similarity zero because
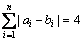
in Eq.(4). However, it is somewhat questionable that the similarity of all pairs in Fig.4 satisfies the degree of similarity satisfy zero with another similarity measure in Eq.(6) or Eq.(7). Additionally, three cases in Fig.4 are not satisfied for the normalized universe of discourse [14-15].
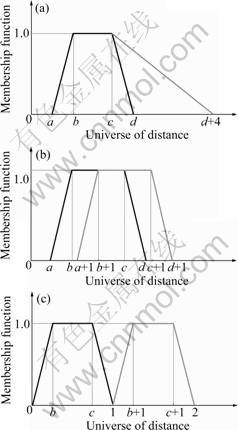
Fig.4 Similarity zero membership function pairs with fuzzy number based similarity: (a) Exact pair except d, d+4; (b) Same shape shift to one; (c) Same shape shift (total length limited in one)
5 Conclusions
1) Two ways of similarity measure design were introduced. The first one was based on fuzzy number, COG, and membership function type, whereas the other was designed by distance measure. Characteristic of conventional similarity measure with fuzzy number was introduced and discussed. It was easy to design because of the particular fuzzy membership type. However, distance based similarity could be applicable to ordinary fuzzy membership functions.
2) Similarity measure was designed through distance measure, and the usefulness of the proposed similarity measure was proved. The designed similarity measure was considered to be two fuzzy data set and fuzzy data set-crisp data.
3) Similarity measure computation was carried out for previous examples, in which fuzzy number based similarity measure was applied. By comparison, it was verified that the proposed similarity measure could be applied to general types of fuzzy membership functions and proper performance was obtained.
References
[1] Rébillé Y. Decision making over necessity measures through the Choquet integral criterion [J]. Fuzzy Sets and Systems, 2006, 157(23): 3025-3039.
[2] Kang W S, Choi J Y. Domain density description for multiclass pattern classification with reduced computational load [J]. Pattern Recognition, 2008, 41(6): 1997-2009.
[3] Shih F Y, Zhang K. A distance-based separator representation for pattern classification [J]. Image and Vision Computing, 2008, 26(5): 667-672.
[4] CHEN S M. New methods for subjective mental workload assessment and fuzzy risk analysis [J]. Cybernetics and Systems, 1996, 27(5): 449-472.
[5] HSIEH C H, CHEN S H. Similarity of generalized fuzzy numbers with graded mean integration representation [C]// Proceedings of the Eighth International Fuzzy Systems Association World Congress. Taipei: IFSA press, 1999, 2: 551-555.
[6] LEE H S. An optimal aggregation method for fuzzy opinions of group decision [C]// Proceedings of 1999 IEEE International Conference on Systems, Man, Cybernetics. Tokyo: Piscataway, IEEE, 1999, 3: 314-319.
[7] CHEN S J, CHEN S M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers [J]. IEEE Trans. on Fuzzy Systems, 2003, 11(1): 45-56.
[8] LEE S H, CHEON S P, KIM J H. Measure of certainty with fuzzy entropy function [J]. Lecture Notes in Artificial Intelligence, 2006, 4114: 134-139.
[9] LEE S H, KIM J M, CHOI Y K. Similarity measure construction using fuzzy entropy and distance measure [J]. Lecture Notes in Artificial Intelligence, 2006, 4114: 952-958.
[10] LIU X. Entropy, distance measure and similarity measure of fuzzy sets and their relations [J]. Fuzzy Sets and Systems, 1992, 52: 305-318.
[11] FAN J L, XIE W X. Distance measure and induced fuzzy entropy [J]. Fuzzy Set and Systems, 1999, 104: 305-314.
[12] FAN J L, MA Y L, XIE W X. On some properties of distance measures [J]. Fuzzy Set and Systems, 2001, 117: 355-361.
[13] LEE S H, RYU K H, SOHN G Y. Study on entropy and similarity measure for fuzzy set [J]. IEICE Trans Inf & Syst, 2009, E92-D(9): 1783-1786.
[14] LEE S H, PARK H J, PARK W J. Similarity computation between fuzzy set and crisp set with similarity measure based on distance [J]. Lecture Notes in Artificial Intelligence, 2008, 4993: 644-649.
[15] PARK H J, LEE S H. Similarity analysis between fuzzy set and crisp set [J]. International Journal of Fuzzy Logic and Intelligent Systems, 2007, 7(4): 295-300.
(Edited by HE Yun-bin)
Foundation item: Project(2010-0020163) supported by Priority Research Centers Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education, Science and Technology
Received date: 2011-02-15; Accepted date: 2011-04-28
Corresponding author: LEE Sang-Hyuk, PhD; Tel: +82-32-860-8829; E-mail: leehyuk@inha.ac.kr