DOI: 10.11817/j.issn.1672-7207.2015.08.021

基于非合作博弈论的CoMP-JP资源分配算法

毕晓君，郭柳，胡菘益

 (哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001)

摘要：为了提高LTE-A系统中协作多点联合处理技术(CoMP-JP)的资源利用率，保证中心用户和边缘用户在资源分配过程中的公平性和QoS需求，提出一种以最大化系统吞吐量为目的中心用户和边缘用户联合处理的动态资源分配方法。首先，在功率给定的情况，每个簇内以保证用户的QoS需求并最大化系统吞吐量为目的进行用户调度；其次，在调度完成后，为了协调用户间的干扰，实现系统的吞吐量的最大化，提出改进代价函数的非合作博弈控制算法，并证明该算法纳什均衡解的存在性与唯一性。实验结果表明：本文算法与现有算法相比，更能满足用户的QoS需求和用户间的公平性，同时获得更高的系统吞吐量。

关键词：协作多点联合处理技术；资源分配；非合作博弈论

中图分类号：TN92             文献标志码：A         文章编号：1672-7207(2015)08-2906-08

Resource allocation algorithm for CoMP-JP based on non-cooperative game theory

BI Xiaojun, GUO Liu, HU Songyi

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract: In order to improve the resource utilization of collaboration multiple point joint processing (CoMP-JP) technique in LTE -A system and guarantee the resource allocation fairness between center users and edge source in the process, a joint processing method for the center users and the edge users of dynamic allocation of resources was proposed, with the purpose of maximizing system throughput. First of all, in the case of a given power, a scheduling algorithm that guarantees the user’s QoS requirements and maximizes system throughput was proposed. Secondly, after the scheduling, a non-cooperative game control algorithm was proposed based on improved cost function. The results show that compared with the existing algorithms, the proposed algorithm performs better in satisfying user's QoS requirements and user fairness, and also has higher system throughput.

Key word: CoMP-JP techique; resource allocation; non-cooperative

3GPP LTE-A下行系统物理层的无线链路多址技术采用的是正交频分多址接入(OFDMA，orthogonal frequency division multiple access)^[1]，由于OFDMA的正交特性，所以每个小区内的资源块是相互独立的，不存在同频干扰。但是，位于小区边缘的用户却受到相邻小区严重的同频干扰，为了解决这个问题，在LTE-A系统中提出了协作多点(CoMP，cooperative multiple point)^[2]技术来改善边缘用户频谱效率、提高小区边缘用户吞吐量。CoMP技术又分为联合处理(JP)和波束赋形(CS)2类，本文算法采用JP技术。此外，有效的资源分配算法在CoMP-JP技术中至关重要。目前，对于CoMP-JP的资源分配尚处于研究的初期阶段，文献[3]提出了在频率复用因子为1情况下系统总容量最大的功率分配算法，但是该算法仅能为1个边缘用户进行联合传输，而实际系统中有多个边缘用户存在，因此限制了其应用范围。文献[4]提出了次优的子载波和最优的功率分配算法，该算法保证了用户间的公平性和系统的吞吐量，但需对系统资源进行划分，不同簇利用不同的资源，这降低了系统资源利用率，造成系统资源浪费。文献[5]提出了CoMP-JP系统中跨层的功率分配，但该算法未对系统的用户调度问题进行研究。博弈论作为解决多个具有利益冲突的局中人的策略选择及均衡的有效数学工具，无论是在认知无线电^[6-7]还是在中继系统^[8]的功率控制方面都已经得到广泛应用。目前，已有学者将博弈论引入到CoMP-JP系统中^[9-10]，提出了基于非合作博弈的资源分配，有效协调了相邻簇相同资源块上的同频干扰，实现了系统吞吐量最大化，但是该算法仅考虑了边缘用户，没有对中心用户的资源进行分配。为此，本文作者提出了一种基于非合作博弈论的CoMP-JP中心用户和边缘用户联合资源分配算法。首先，提出了一种兼顾用户公平性与用户QoS需求并以最大化系统吞吐量为目的系统资源分配算法。其次，在资源块分配完成后，各基站以最大化系统吞吐量为目的进行注水功率分配。但由于用户之间存在同频干扰，所以采用非合作博弈协调各个基站在资源块上的发射功率，实现系统的吞吐量最大，此外，通过改进定价函数，在保证了系统的吞吐量的同时，进一步提升了用户间的公平性。

1  CoMP-JP资源分配模型

1.1  协作多点蜂窝系统模型

协作多点(CoMP)蜂窝系统模型如图1所示。在系统中共有M个小区，每个簇中有A个小区，所以共有C(C=M/A)个簇，每个基站位于小区的中心位置，每个小区中的用户分为2类，一类是中心用户，另一类是边缘用户。所有用户都随机的分布在小区内，每个小区的频率复用因子为1，所有的基站和用户都在单天线模式下通信，且小区中的中心用户仅由它所在的小区内的基站为其提供服务，而为了减少小区中的边缘用户所受的同频干扰，边缘用户由它所在簇中的所有基站为其提供服务。

假设系统的带宽为B，资源块的数量为R，由于在同一簇中所有小区的基站都在同一个资源块上为1个边缘用户服务，并且在1个簇中1个资源块只分给1个边缘用户，所以不存在簇内干扰，但是在不同的簇中仍可使用这个资源块，因此，对于边缘用户，不同的簇间存在同频干扰。而对于中心用户，仅有它所在的小区为其提供服务，因此，中心用户存在小区间的同频干扰。

图1  CoMP蜂窝系统模型

Fig. 1  CoMP Cellular system model

1.2  CoMP-JP资源分配问题的数学模型

假设每个小区中有N_c个中心用户，N_e个边缘用户，随机的分布在小区中。每个小区的边缘用户和中心用户都可以通过基站的控制信令获得小区内用户的信道信息，但无法获知其他小区的信道信息，并且信道增益在一段时间内是不变的，因此，在小区k中中心用户的信噪比(SINR)^[10]为

      (1)

其中：为小区k中用户i在资源块R_i上的信噪比；为在资源块R_i上小区k中的基站分配给本小区用户i的功率；为在资源块R_i上小区k中的基站分配给小区j中用户i的功率；和分别为小区k到本小区用户i的信道增益和小区j到小区k中用户i的信道增益；δ²为信道内的高斯白噪声功率；为小区k中用户i受到的干扰总和。对于边缘用户，整个簇中的基站都知道边缘用户的信道信息，因此，边缘用户的SINR表示为

            (2)

其中：，为簇c中的用户i受到的来自其他簇的干扰与高斯噪声功率之和；和分别为簇j中基站m对簇c中用户i的发射功率和簇c中基站m对簇c中用户i的发射功率；和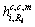分别表示簇j中基站m到簇c中用户i的信道增益和簇c中基站到簇c中用户i的信道增益。

当采用M-QAM 调制方式^[11]时，在误码率(R_BE) 给定的情况下，可以得到，根据香农定理，中心用户i和边缘用户i在资源块上的传输速率分别为：

         (3)

         (4)

进行资源分配的目标是在保证用户的服务质量(QoS)和公平性的基础上，通过合理的用户调度和功率协调，达到最大化系统吞吐量的目的。

综上所述，CoMP-JP资源分配的数学模型可用下式表示：

          (5)

式中：为中心用户或者是边缘用户i在资源块R_i上的速率；为在资源块R_i上所调度的所有用户的集合。目标函数是在满足约束条件的基础上最大化系统的吞吐量。约束条件1表示用户的传输速率需求范围，约束条件2表示每个小区在资源块上的分配的功率之和不能超过基站的发射功率上限。

2  CoMP-JP系统用户调度和功率分配博弈的实现

由式(5)可以看出，要实现最大化系统吞吐量的目的就要进行资源块和功率的联合优化，但是2个参数的二维优化不仅计算复杂度高，而且极大的增加系统的开销，并且很难实现。为此，本文将用户调度和资源分配分开进行。第1步，在功率给定的条件下进行子载波分配；第2步，在子载波分配完成后进行功率的调整。

2.1  在单个簇内用户调度实现

首先，将各基站的最大功率平均分配在各个资源块上，由于每个小区内的资源块是相互独立的，通过最大化每个资源块上的吞吐量，实现最大化系统吞吐量的目的。因此，在每个用户的干扰给定的情况下式(5)可以简化为如下形式：

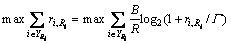
           (6)

由式(6)可以看出：用户调度的原则是在满足用户QoS要求并保证用户间的公平性的前提下，调度信噪比最大的用户，实现每个资源块上的吞吐量最大化。

文献[12]中提出的中心用户和边缘用户联合调度的用户调度算法兼顾了用户的公平性和系统的吞吐量，但是算法中未考虑用户的QoS需求，因此本文在文献[12]的基础上提出了一种保证用户QoS需求，避免资源浪费，同时能最大化系统吞吐量的调度算法。

本文调度用户所依据的准则为

         (7)

式中：U为单位阶跃函数，当时，，否则，。式(7)中第1部分的目标是最大化系统的吞吐量，第2部分的目标是保证用户的QoS需求即最小速率需求。第2部分的优先级高于第1部分，因此，本文所提算法在满足用户的QoS需求的基础上，实现最大化系统吞吐量的目的。并且在资源充足时，当所有用户都满足了最小速率需求时，将以满足用户最大速率为目标进行剩余资源的再分配，实现满足用户最大速率的目标。其次，当所有用户的最大速率需求均满足，剩余的资源就是节约的资源。本文所提调度算法以簇为单位进行资源块的分配，p_i越大，簇中用户i拥有的调度优先级越高，在进行用户调度时，每次都是找出簇中拥有优先级最高的用户为其分配资源。具体实现步骤如下。

1) 将资源块以满足用户需求和系统吞吐量最大化进行分配。

对于任意的资源块R_i(，j=0)：

① 在簇c(j)中计算所有用户的在资源块R_i上的传输速率和用户k分得资源块R_i后的传输速率R_k。

② 若R_k大于用户的最大许可速率，则P_k=0；否则，根据式(7)计算用户的优先级P_k。

③ 选出优先级最高的边缘用户e和当前簇中每个小区内优先级最高的中心用户c₁，c₂，c₃。判断3×p_e≤是否成立，若成立则执行步骤④，否则执行步骤⑤。

④ 分别判断，，。若 =0，则，其中：为剩余资源块集合，否则；若=0，则，否则；若=0，则，否则，执行步骤⑥。

⑤ ；

⑥ 若j=C，则结束，否则j=j+1，返回到步骤①。

2) 将剩余资源块以实现用户的最大需求进行再分配。

对于任意的资源块R_i，，j=0

① 在簇c(j)中，若为非，则将R_i分给用户k₁，k₁满足式(8)，其中。

           (8)

② 若j=c，则结束，否则j=j+1，返回到步骤①。

2.2  CoMP-JP的功率分配算法博弈

从式(6)可知，为了实现吞吐量最大化的目的，当用户调度完成后，下一步需要进行的是功率分配。然而，同一资源块上的用户都希望通过增加自己的发射功率，从而增加自己的传输速率，但是，用户在增加自己发射功率的同时会增加该资源块上其他用户的同频干扰。这不仅增加了系统的发射功率，而且降低了系统的吞吐量，使系统的功率效率极低。为此，引进考虑定价函数的非合作博弈，对发射功率大且产生干扰大的用户进行惩罚，协调用户间的发射功率，实现在较低的发射功率下系统的吞吐量最大化。

2.2.1  非合作功率分配博弈模型的建立

非合作博弈论有3个重要的组成部分：博弈参与者、策略空间和效用函数，经过博弈要达到一种均衡，也就是利益的最大化。本文通过建立功率分配博弈模型完成系统的功率分配。功率分配博弈模型中3部分的意义如表1所示。

但需注意的是对于CoMP-JP功率分配博弈同一资源块上的用户可能是中心用户，也可能是边缘用户，若是边缘用户，它的效用函数是3个协作基站发射功率的函数。

综上所述，CoMP-JP博弈问题可以表示为，其中，N为不同小区内的同一个资源块上的用户，P为用户的发射功率，为用户在资源块上获得的吞吐量。

表1  CoMP-JP功率分配与博弈论的对应关系

Table 1  Corresponding relation of CoMP-JP power allocation and game theory

2.2.2  代价函数的设计

为了防止用户在自私地增加自己的功率的同时增加其他用户的同频干扰，需要对发射功率较大并且对其他用户产生干扰的用户进行惩罚，发射功率越大，被惩罚的力度越大，因此，代价函数应该是发射功率的函数，但若只是发射功率，会使发射功率大的用户受到更多的惩罚，系统的吞吐量有所增加，但用户间的公平较差，为此，文献[9]中将信道增益引进代价函数中，提升用户间的公平性。在此基础上，为了进一步提升用户间的公平性，本文将SINR作为代价函数。这是由于SINR不仅与发送功率、链路增益有关还与干扰功率有关 ，并且它与用户在资源块上的速率有更直接的关系，因此，信噪比越大的用户，受到的惩罚越大，信噪比越小的用户，受到的惩罚越小，避免了信噪比大的用户占用过多的资源，信噪比小的用户分不到资源，有效保证了用户间的公平性。基于此，代价函数的式可表示为

            (9)

但由于资源块上可能存在中心用户和边缘用户，因此定义中心用户和边缘用户的净效益函数U_m,i和U_c,i分别为：

       (10)

       (11)

为了兼顾系统的吞吐量，在进行功率分配博弈前，且不考虑小区间干扰的情况下，在每个小区内进行以吞吐量最大化为目的的注水功率分配，来获得用户的注水功率p_i,WF作为用户的最大发射功率，因此，用户的策略空间范围是[0，p_i,WF]。

2.2.3  Nash均衡的存在性与唯一性证明

本文采用博弈论的目的是获得纳什均衡点，也就是所有博弈者此时的策略所组成的集合是最优的，任何一个博弈方单独改变策略都会导致整体受损，也就是达到纳什均衡时，系统整体的吞吐量最大。下面证明所提出的改进代价函数的非合作功率分配博弈Nash均衡的存在性与唯一性。

定理1  Nash均衡的存在性。

博弈论满足以下2个条件，所提出的博弈模型就存在Nash均衡点^[13]：

1) P是欧几里得空间的R^N中非空、闭合、有界的凸集。

2) 效用函数，在P上是连续的，在p_i上是拟凹的。

证明：由于每个用户的策略空间p_i的范围是[0，p_WF]，显然满足条件1)。

在P上是连续的，由条件2)可知，只需证明在p_i上是拟凹的。

对于中心用户，

对于边缘用户，

当效用函数的一阶导数等于0时，可得优化解。中心用户优化解为

       (12)

边缘用户的优化解为

 (13)

对效用函数求二阶导数，其中，中心用户为

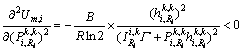
边缘用户为

由于二阶导数小于0 ，因此效用函数是拟凹的，由此可知，本文所提博弈模型的Nash均衡的存在性。

证明纳什均衡唯一性的关键是证明最优响应函数是标准函数，即满足正性、单调性和可量测性^[13]。

设当中心用户取得Nash均衡点是，则，显然满足正性和单调性，只需证明可量测性。

对任意，

所以，对任意，满足，即是可测的，同理可证边缘用户取得Nash均衡点也具有可量测性。

由此可证明，本文提出的功率分配博弈的Nash均衡点是唯一的。

2.3  CoMP-JP 功率分配博弈的价格函数

由于策略空间的范围是[0，p_i,WF]，再由式(12)可知，价格函数λ_i为：

，

由于，可得

      (14)

2.4  CoMP-JP 功率分配算法博弈步骤

求解纳什均衡点的具体实现步骤如下。

1) 对任一个资源块R_i，在初始时刻t=0,设置各个基站的初始功率为p₀，同时设定极小值ε。

2) 在t=t+1时，判断用户为边缘用户还是中心用户，如是中心用户，根据式(12)更新用户的发射功率，若是边缘用户，则根据式(13)更新用户的发射功率，得到发射功率p_i(t+1)。

3) 对所有用户，若成立，则p_i(t+1)为最终的功率，否则返回步骤2)继续迭代，直到所有用户都满足要求为止。

综上，CoMP-JP 资源分配的整体流程如图2所示。

图2  CoMP-JP 资源分配的整体流程图

Fig. 2  Overall flow chart of CoMP-JP resource allocation

3  实验仿真与分析

为了验证本文提出算法的有效性和先进性，进行一系列的仿真实验，实验分2部分进行：第1部分，验证本文调度算法的有效性和先进性，并与目前效果较好的文献[12]进行对比；第2部分，验证改进代价函数的功率分配博弈算法的有效性，并与目前效果较好的文献[9]中应用的博弈算法-MSP算法进行对比。

采用图1所示的12小区组成的4个固定簇的多小区系统，基站位于小区的中央，每个小区中心用户和边缘用户数分别为2和1。具体的实验参数见表2。

表2  系统基本参数设置

Table 2  System basic parameters set

3.1  单个簇内调度算法的对比及分析

为了验证本文调度算法的有效性和优越性，将本文算法与文献[12]的调度算法进行比较。

为了客观评价用户间的公平性，引入公平性因子作为评价指标^[14]：

       (15)

实验中将所有用户的速率需求设为相同值，用户最小速率为R_min，用户最大速率为R_max。分别在用户速率取不同值时对比2种算法的性能。对比结果见表3。

从表3可以看出：当R_min=0，R_max=+∞时，也就是没有速率要求时，本文算法的系统吞吐量极高，用户间公平性较差。这是由于在没有速率要求时，本文算法是以系统吞吐量最大为目的；当R_min=1×10⁴，R_max=+∞时，即有较低的最小速率需求，且没有最大速率需求，本文算法和对比算法均能满足最小速率需求，此时两者的公平性相近，但是本文算法的系统吞吐量较高，这是由于在满足所有用户的最小需求后，所提算法是以系统吞吐量最大为目标，所以，获取较大的系统吞吐量；在最小速率升高而仍没有最大速率需求时，本文算法满足了所有用户的最小速率需求，而对比算法中有19.5%的用户没有满足最小速率需求，也正因为这个原因，此时本文算法的系统吞吐量和用户间的公平性都高于对比算法；在R_min=1×10⁴，R_max=4×10⁴时，由于本文算法考虑了在达到用户最大速率以后将剩余资源重新分配，因此在节省了5%的资源的情况下，仍比对比算法的系统吞吐量高；当R_min=1×10⁴，R_max=4×10⁴时，本文算法在满足用户最小速率需求和节省资源的情况下，系统吞吐量和公平性都高于对比算法。

表3  调度算法性能比较

Table 3  Scheduling algorithm performance comparison

综上所述，本文算法与文献[12]算法相比，在有用户速率限制的情况下，能满足用户的速率需求的，并且得到更大的系统吞吐量和用户间的公平性；在资源充足时，本文算法在节省资源的同时，可获得较高的系统吞吐量，说明本文算法优于对比算法。

3.2  基于改进定价因子的非合作功率博弈算法实验对比及分析

为了验证本文改进代价函数的功率分配博弈的有效性和先进性，将本文算法与MSP算法相比较。对博弈算法的验证是在本文所提调度算法的基础上完成，其中参数设置分别为，R_min=2×10⁴，R_max=7×10⁴，p₀= 1×10^-3，ε=1×10^-5。

图3和图4所示分别为权衡参数a与系统吞吐量和用户间公平性的关系。

从图3可以看出：当a=0时，功率分配博弈没有起作用，此时本文算法等同于WF算法，随着a增加，系统的吞吐量有所增加，这是因为功率分配博弈开始起作用，有效地协调了小区间的同干频。从图3还可以看出，在a=0.2附近时，系统的吞吐量趋近最大值，因此，可以把此时的a作为最佳权衡参数，由此得到的价格也是获取最大吞吐量的最佳价格。

由图3可知：本文算法的系统吞吐量略小于对比算法。但从图4发现本文算法获得了较好的公平性。这是因为本文的代价函数是信噪比，信噪比越大的用户会受到越严重的惩罚，所以相应的用户在资源块上的速率就会减小，从而系统的吞吐量就会降低。但对于公平性来说，对信噪比越大的用户惩罚越大，对信噪比越小的用户惩罚越小，这有效防止了信噪比大的用户分配过多的资源，保证了信噪比小的用户分得一定量的资源，实现了用户间的公平性。

图3  a与系统吞吐量的关系

Fig. 3  Relationship beteeen a and system throughput

图4  a与公平性因子的关系

Fig. 4  Relationship between a and fairness factor

综上，与MSP算法相比，本文算法的系统吞吐量略小，但a取最佳值时，本文算法的系统吞吐量仍达到较大值。且在a取不同值时，本文算法的公平性都高于对比算法，说明本文算法优于对比算法。

从2个实验结果可以看出：在有用户速率需求时，本文算法不仅能满足用户的速率需求，而且在系统吞吐量和用户公平性上都优于对比算法；在资源充足时，本文算法既能节约资源，又能获得较高的系统吞吐量和用户间的公平性。在此基础上，通过博弈算法协调用户的发射功率，进一步提升了系统的吞吐量，与对比算法相比，提高了用户间的公平性。

4  结论

1) 提出了满足用户速率需求并最大化系统吞吐量的调度算法。所提算法实现了在保证用户QoS需求和用户间公平性的基础上最大化系统吞吐量的目的。

2) 通过改进非合作博弈的代价函数协调用户间的同频干扰，建立了非合作功率分配模型，证明了Nash均衡的存在性和唯一性，最终实现了在保证系统吞吐量的同时，进一步提升了用户间的公平性的目的，在CoMP-JP资源分配问题上具有一定的应用价值。

参考文献：

[1] 3GPP TR36.913. Requirements for further advancements for E-UTRA[S].

[2] 3GPP R1-082896. Coordinated multicell transmission for LTE-advance downlink[S].

[3] Luo B, Cui Q, Wang H, et al. Optimal joint water-filling for coordinated transmission over frequency-selective fading channels[J]. Communications Letters, 2011, 15(2): 190-192.

[4] 张晓亮, 纪红. 多蜂窝系统下行多用户CoMP 中一种次优的子载波和功率分配算法[J]. 北京邮电大学学报, 2012, 35(4): 1-5.

ZHANG Xiaoliang, JI Hong. A sub-optimal sub-carrier and power allocation for the downlink multi-user CoMP in multi-cellular systems[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 1-5.

[5] 朱国晖, 李佳蔚, 赵季红. LTA-A系统中基于CoMP的下行跨层功率分配优化方法[J]. 计算机工程与设计, 2012, 33(10): 3703-3707.

ZHU Guohui, LI Jiawei, ZHAO Jihong. Cross-layer optimization power allocation methods based on CoMP downlink in LTA-A system[J]. Computer Engineering and Design, 2012, 33(10): 3703-3707.

[6] 彭永祥, 段翰聪. 认知无线电网络非协作博弈功率分配算法研究[J]. 小型微型计算机系统, 2012, 33(5): 1029-1033.

PENG Yongxiang, DUAN Hancong. Power allocation algorithm for cognitive radio networks based on non-cooperative game[J]. Journal of Chinese Computer System, 2012, 33(5): 1029-1033.

[7] Akyildiz I F, Lee W Y, Vuran M C, et al. Next generation/dynamic spectrum access/cognitive radio wireless networks: A survey[J]. Computer Networks, 2006, 50(13): 2127-2159.

[8] 向征, 方旭明, 徐鹏. 基于非合作博OFDMA无线多跳中继网络上行链路资源分配算法[J]. 通信学报, 2012, 33(3): 67-74.

XIANG Cheng, FANG Xuming, XU Peng. Resource allocation algorithm based on non-cooperative game in uplink OFDMA multi-hop relay networks[J]. Communication Journal, 2012, 33(3): 67-74.

[9] Fu S, Wu B, Ho P H, et al. Interference coordination in CoMP with transmission scheduling and game theoretical power reallocation[C]//2012 IEEE International Conference on Communications (ICC), Ottawa: IEEE, 2012: 4212-4217.

[10] Haddadi S, Behroozi H, Khalaj B H. Power allocation in coordinated multi-cell networks using Stackelberg game[C]//2012 Sixth International Symposium on Telecommunications (IST). Piscataway: IEEE, 2012: 289-294.

[11] A, Pap L. General interference analysis of M-QAM and M-PSK wireless communications[J]. Wireless Networks, 2013, 19(3): 331-344.

[12] Liu J, Chang Y, Pan Q, et al. A novel transmission scheme and scheduling algorithm for CoMP-SU-MIMO in LTE-A system[C]//2010 IEEE 71^st Vehicular Technology Conference (VTC 2010-Spring). Piscataway: IEEE, 2010: 1-5.

[13] 胡图, 景志宏. 一种改进的认知无线网络功率控制博弈算法[J]. 计算机科学, 2012, 39(2): 75-78.

HU Tu, JING Zhihong. Improved power control game algorithm in cognitive wireless networks[J]. Computer Science, 2012, 39(2): 75-78.

[14] 仲崇国, 李春国, 杨绿溪. 基于非合作博弈论的多小区OFDMA 系统动态资源分配算法研究[J]. 电子与信息学报, 2009, 31(8): 1935-1940.

ZHONG Chongguo, LI Chunguo, YANG Lüxi. Dynamic resource allocation algorithm for multi-cell OFDMA systems based on non-cooperative game theory[J]. Electronics and Information Technology Journal, 2009, 31(8): 1935-1940.

(编辑  赵俊)

收稿日期：2014-08-09；修回日期：2014-11-15

基金项目(Foundation item)：国家自然科学基金资助项目(61175126)；中央高校基本科研业务费专项(HEUCFZ1209)；教育部博士点基金资助项目(20112304110009)(Project (61175126) supported by the National Science Foundation of China; Project (HEUCFZ1209) supported by the Fundamental Research Funds for the Central Universities; Project (20112304110009)supported by the PhD Program Foundation of Ministry of Education of China)

通信作者：毕晓君，教授，博士生导师，从事智能信息处理研究；E-mail：bixiaojun@hrbeu.edu.cn