Energy analysis of rock plug thickness in karst tunnels based on non-associated flow rule and nonlinear failure criterion
来源期刊:中南大学学报(英文版)2017年第12期
论文作者:许敬叔 YANG Zi-han(杨子汉) 张睿 YANG Xiao-li(杨小礼)
文章页码:2940 - 2950
Key words:karst tunnel; water inrush; safe thickness of rock plug; upper bound theorem; nonlinear failure criterion; non-associated flow rule
Abstract: The geological hazards, such as water inrush and mud outburst, are easily induced by the high water pressure caverns ahead of a karst tunnel face. Therefore, it is a pivotal issue to determine the reserved thickness of rock plug during the construction of tunnels. The limit analysis principle is employed to analyze the safe thickness from the point of energy dissipation, and the nonlinear and non-associated characteristics of geotechnical materials are both considered. On the basis of a plane failure pattern of rock plug, the expressions of detaching curve and rock plug thickness are derived. The effect of each parameter on the safe thickness of rock plug is discussed in detail, which interprets the corresponding failure scope of rock plug. The obtained results indicate that the thickness of rock plug is highly influenced by the nonlinear dilatancy coefficient and the nonlinear coefficient. The proposed method is validated by a comparison of the calculated results with those of the engineering project of the “526 karst cavern” of Yunwushan tunnel. This proposed method can provide reference basis for the design and excavation of karst tunnels in the future.
Cite this article as: YANG Zi-han, ZHANG Rui, XU Jing-shu, YANG Xiao-li. Energy analysis of rock plug thickness in karst tunnels based on non-associated flow rule and nonlinear failure criterion [J]. Journal of Central South University, 2017, 24(12): 2940–2950. DOI:https://doi.org/10.1007/s11771-017-3708-1.
J. Cent. South Univ. (2017) 24: 2940-2950
DOI: https://doi.org/10.1007/s11771-017-3708-1
YANG Zi-han(杨子汉), ZHANG Rui(张睿), XU Jing-shu(许敬叔), YANG Xiao-li(杨小礼)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: The geological hazards, such as water inrush and mud outburst, are easily induced by the high water pressure caverns ahead of a karst tunnel face. Therefore, it is a pivotal issue to determine the reserved thickness of rock plug during the construction of tunnels. The limit analysis principle is employed to analyze the safe thickness from the point of energy dissipation, and the nonlinear and non-associated characteristics of geotechnical materials are both considered. On the basis of a plane failure pattern of rock plug, the expressions of detaching curve and rock plug thickness are derived. The effect of each parameter on the safe thickness of rock plug is discussed in detail, which interprets the corresponding failure scope of rock plug. The obtained results indicate that the thickness of rock plug is highly influenced by the nonlinear dilatancy coefficient and the nonlinear coefficient. The proposed method is validated by a comparison of the calculated results with those of the engineering project of the “526 karst cavern” of Yunwushan tunnel. This proposed method can provide reference basis for the design and excavation of karst tunnels in the future.
Key words: karst tunnel; water inrush; safe thickness of rock plug; upper bound theorem; nonlinear failure criterion; non-associated flow rule
1 Introduction
In the highly developed karst areas, the rock mass, in particular limestone, which easily suffers from the corrosion, washout and replenishment of underground water, tends to induce caverns with high pressure and rich water. When tunnels are constructed in these areas, under the effect of high water pressure in the karst caverns, it is vulnerable to induce failure at the tunnel face or at the side wall associated with water inrush and mud outburst. Consequently, a certain distance between the tunnel structure and the caverns, namely safe thickness of rock plug, should be determined to keep a safe construction. For tunnels excavated in this kind of condition, it is a non-ignorable technical problem to determine a proper safe thickness of rock plug on the basis of geophysical prospecting.
Currently, there are mainly four approaches for the determination of safe thickness of rock plug, including experience analogism, numerical simulation, model test and theoretical calculation. LIU and PENG [1] employed the linear regression principle to investigate the minimum safe thickness, and presented three quantitative methods for calculating the safe distance. WU et al [2] performed numerical simulation on the case of underground water inrush from fracture section to the coal mine floor, and analyzed the mechanism of water inrush. LI et al [3] analyzed the mechanism of water inrush by a model test and suggested that the safe areas of rock plug should be divided into relaxation section, safe thickness section and fracture belt section. MEGUID and DAND [4] used elastic-plastic finite element theory to investigate the effect of holes generated by dissolution of carbonate layer on tunnel lining, and found that the size of holes is the principal factor to affect circumferential stress of tunnel lining. To sum up, these methods have both merits and demerits, while there are still no widely-accepted theoretical approaches for computing the safe thickness of rock plug available.
In recent years, the limit analysis theorem has been broadly utilized in geotechnical engineering due to its unique advantages [5–8]. FRALDI and GUARRACINO [9] established the curved failure mechanism for roof collapse based on limit analysis theory, and derived the failure shape for tunnel cross sections. PAN and DIAS [10] employed spatial discretization technique to improve the three-dimensional failure mode proposed by LECA and DORMIEUX [11] and SOUBRA [12], and calculated the upper bound solution of supporting pressure. YANG et al [13–16] introduced generalized tangential technique with nonlinear failure criterion to perform further research on the stability of tunnels, slopes, and foundations with limit analysis method.
However, the existing researches are mostly based on the linear Mohr-Coulomb (M-C) failure criterion and associated flow rule. According to the upper bound theorem, the geo-materials obey the associate flow rule during plastic flow, which results in a bigger dilatancy than the actually measured value. And together with the influences of nonlinear properties for geo-materials, the calculated results are normally unsafe. Moreover, intensive investigations have demonstrated that geo-material is a kind of nonlinear material which generally obeys non-associated flow rule [17]. Some scholars have conducted preliminary studies on the tunnel stability problems under this circumstance [18–20]. But, there are rare researches on the safe thickness of rock plug in the condition that the surrounding rock obeys nonlinear failure criterion and non-associated flow rule.
This work adopts limit analysis theorem to study on this engineering problem. Based on the constructed failure mechanism of rock plug, the computation expression of the safe thickness of rock plug is deduced. Subsequently, parametric analysis is performed to analyze the effect of each parameter on the safe thickness of rock plug and failure scope. At last, an engineering example is introduced to verify the method proposed in this paper. The calculation method could provide reference basis for the design and construction of karst tunnels in the future.
2 Limit analysis with nonlinearity and dilation
2.1 Upper bound theorem of limit analysis
Limit analysis theory includes upper and lower bound theorems. Its obvious advantage is that a practical failure load can be calculated regardless of the complicated geometrical shape of structures and loading conditions. This theory is a feasible approach to resolve stability of engineering problems. In this work, upper bound theorem is employed to determine the safe thickness of rock plug in the karst cavern filled with water. The upper bound theorem states that, when the suggested kinematically admissible velocity field satisfies the deformation condition, the load calculated by equating the internal energy dissipation rate to the external work rate is no less than the actual load under the limit state. Its expression reads
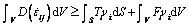 (1)
(1)
where 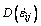 is the internal energy dissipation rate per volume; Ti and Fi are external surface and volume force, respectively; vi denotes the velocity vector in the kinematically admissible velocity field.
is the internal energy dissipation rate per volume; Ti and Fi are external surface and volume force, respectively; vi denotes the velocity vector in the kinematically admissible velocity field.
2.2 Power-law failure criterion
Geotechnical materials are frictional materials and mainly show shear failure. Normally, the linear M-C failure criterion is adopted to characterize the shear strength of geotechnical materials in the field of engineering. However, plenty of researches indicate that the actual relationship between shear stress and normal stress is nonlinear. AGAR et al [21] utilized the power law to describe this nonlinear relationship of geotechnical materials on the basis of laboratory tests. The power-law (P-L) failure criterion in stress space can be represented as
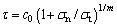 (2)
(2)
where c0 is initial cohesion; σt means axial tensile strength; σn and τ are normal and shear stresses in the shear surface, respectively; m is the nonlinear coefficient which determines the crook degree of strength envelope. When m=l.0, the nonlinear P-L failure criterion is reduced to linear M-C criterion.
2.3 Nonlinear failure criterion with non-associated flow rule
In plastic theory, the flow rule is defined to determine the direction of plastic strain increment, or the proportional relation among the components of plastic strain increment tensor. The limit analysis based on the classical plastic theory assumes that the research objects obey the associated flow rule during plastic deformation, namely yield surface coinciding with plastic potential surface. The plastic strain increment is then normal to the plastic potential surface. In the calculation, it will lead to a bigger dilatancy than the actual measured one.
Generally, there are two ways to introduce the non-associated property of geotechnical materials in the realm of limit analysis [22]. The first idea is to remain the failure criterion unchanged and calculate with non-associated flow rule directly. This method involves a complex calculation procedure which makes it not easy to perform. The other one modifies the failure criterion firstly and then conducts the calculation which follows the same progress of the associated flow rule. The second method is a more genetic way compared to the first one. In order to take the non-associated property of geotechnical materials into consideration, DRESCHER and DRTOURNAY [23] modified the linear M-C failure criterion. It is represented as
 (3)
(3)
where c and φ are the cohesion and internal frictional angle, respectively; c* and φ* are the modified cohesion and modified internal frictional angle. η represents the dilatancy coefficient. Equation (3) is reduced to the well known M-C failure criterion when the value of η is equal to 1.0. The essential of this idea is a proportional reduction of shear strength c and φ. As for the coaxial non-associated material, the strength envelops of M-C and modified M-C failure criterion are illustrated in Fig. 1.
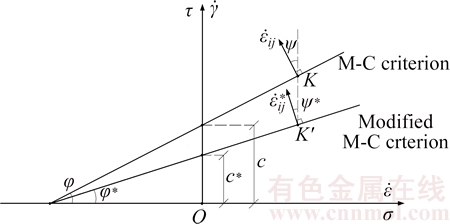
Fig. 1 Strength envelops and flow rule of Mohr-Coulomb failure criterion
As shown in Fig. 1, ψ denotes the dilatancy angle,  and
and  respectively are plastic strain rate before and after the modification. However, geotechnical materials show obvious nonlinear character. Thus, it is of certain theoretical value to conduct researches on the non-associated features of geotechnical materials under the nonlinear failure criterion. The second way which modifies failure criterion is adopted in this work and the P-L failure criterion is modified by introducing a nonlinear dilatancy coefficient ζ. The modified P-L failure criterion is expressed as
respectively are plastic strain rate before and after the modification. However, geotechnical materials show obvious nonlinear character. Thus, it is of certain theoretical value to conduct researches on the non-associated features of geotechnical materials under the nonlinear failure criterion. The second way which modifies failure criterion is adopted in this work and the P-L failure criterion is modified by introducing a nonlinear dilatancy coefficient ζ. The modified P-L failure criterion is expressed as
 (4)
(4)
where ζ is a constant between 0 and 1.0. Equation (4) is reduced to P-L failure criterion when the value of ζ is equal to 1.0. The strength envelops of original and modified P-L failure criterion are illustrated in Fig. 2.
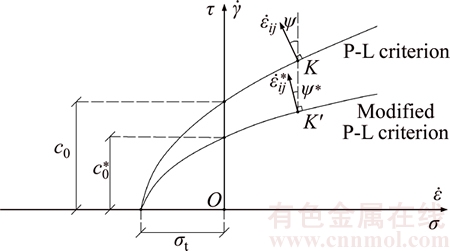
Fig. 2 Strength envelops and flow rule of Power-Law failure criterion before and after modification
It is also worth mentioning that coefficients ζ and η are different.ζ represents the nonlinear dilatancy coefficient, and η is the linear one. Moreover, coefficient η has specific expression. For coaxial non-associated materials [23], it is
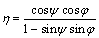 (5)
(5)
As for non-coaxial non-associated materials [23], it is
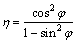 (6)
(6)
While the expressions above do not work for ζ, it should be determined according to the engineering practice and empirical parameters. Coefficient ζ has no computational formulas.
3 Energy analysis of rock plug thickness
After the modification of nonlinear failure criterion, the following work is to deduce the computational formula for the safe thickness of rock plug on the basis of limit analysis. The analysis method used by FRALDI and GUARRACINO [9] to estimate the collapse scope of tunnel roof is extended to investigate the rock plug thickness. The obvious merit of this method is that no additional assumption on the detaching curve of failure mode is required a priori. It can be derived by upper bound theorem and mathematical approach, and thus the failure scope can be finally determined.
The general ideal to calculate the safe thickness of rock plug is as follows [24–27]:
1) Establishing the plane failure mode with the boundary detaching curve;
2) The calculation of the internal energy dissipation and the rate of external work to build the objective function based on upper bound theorem;
3) Employing variational principle to compute the extreme value and derive the analytical expression of detaching line;
4) Calculating the safe thickness of rock plug and the corresponding failure dimension under corresponding boundary conditions.
3.1 Determination of failure mode
For the tunnels with fixed design alignment, it can be suggested that the position of karst caves is random, which means that the caverns could appear randomly around the tunnel face. The mechanical model for the calculation of safe thickness is different for different locations of cavern. Thus, this work takes the special condition, where high-pressure water-rich cavern is right ahead the tunnel face, as an example. The two-dimensional symmetrical failure mode of rock plug is illustrated in Fig. 3.
It can be seen from Fig. 3(a) that under the effect of cavity pressure p, the rock plug in front of tunnel face shows an integral extrusion-type failure. The failure surface is composed by two unknown detaching curves f(x) and f(–x), which are symmetric with respect to y-axial. In order to simplify the calculation, only half of the rock plug is taken as the research object. A local coordinate system s–n is established on the micro-unit of detaching layer (Fig. 3(b)), which takes the tangent and outward normal as the positive directions. Therefore, the algebraic equation between θ and f ′(x) is
 (7)
(7)
In Fig. 3, D represents the height of tunnel cross-section; qcr denotes the tunnel face supporting pressure; w is the hypothetical detaching thickness of rock plug failure; L is the scope of cavity pressure and H is the safe thickness of rock plug, which are two variables to be determined in this work. Moreover, the distribution of pore pressure is assumed to be uniform and vertical to the cavern surface. And the stress surface is also simplified into a plane, namely the dotted line in Fig. 3(a) which is coincident with x-axis.

Fig. 3 2D symmetric failure mode for rock plug:
3.2 Construction of objective function
In order to establish the objective function for the detaching curve, the rate of internal energy dissipation and external work rate should be calculated under the given failure mode. The detail calculation procedure is performed in the following analysis.
In the calculation process of internal energy dissipation, it is easy to find that the whole internal energy dissipates over the detaching layer within thickness w. Taking a micro-unit around the detaching line as the research object, the deformation mode of detaching layer is shown in Fig. 3(b). The micro-unit moves from the dotted line (state 1) to the solid line (state 2) with velocity v, and the detaching layer shows shear deformation along the tangential direction and tensile deformation in normal direction. As a consequence, the energy dissipation rate of this micro-unit can be expressed as
 (8)
(8)
where l is the area of corresponding detaching layer and its value equals to w; 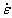 and
and  respectively denote normal and tangential strain rates. According to the definition and triangular relations,
respectively denote normal and tangential strain rates. According to the definition and triangular relations, 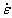 and
and  are expressed as
are expressed as
 (9)
(9)
where vn and vs are normal and tangential velocities of the micro-unit, respectively. Besides, due to the general rule in geotechnical engineering that the compressive strain is positive and the detaching layer produces tensile deformation during the shear failure of rock plug, the value of 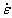 is negative. It demonstrates from another perspective that geotechnical materials expand during plastic deformation, namely the dilatancy effect. Because the associated flow rule will overestimate this dilatancy, it is necessary to take the influences of non-associated flow rule into account.
is negative. It demonstrates from another perspective that geotechnical materials expand during plastic deformation, namely the dilatancy effect. Because the associated flow rule will overestimate this dilatancy, it is necessary to take the influences of non-associated flow rule into account.
This work adopts the idea of modifying failure criterion to consider the influence of non-associated flow rule. It not only meets the basic assumptions of limit analysis, but also can ensure that the yield surface is coincident with the potential surface. Therefore, as for the modified P-L failure criterion, the plastic potential function g(τ, σn) can be expressed as
 (10)
(10)
According to normal flow rule, the normal and tangential strain rates can be also represented as
 (11)
(11)
where λ is a plastic proportion coefficient which is larger than zero. Combing Eq. (9) and Eq. (11), the expression of normal stress of a micro-unit along the detaching line can be derived by dividing out λ and w.
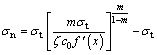 (12)
(12)
After that, by substituting Eqs. (4), (9) and (12) into Eq. (8), the internal energy dissipation of the micro-unit in the velocity discontinuity line f(x) can be calculated as

 (13)
(13)
Based on the formula for curve integral, 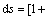
 the whole internal energy dissipation is derived by integrating Eq. (13) along the overall detaching line.
the whole internal energy dissipation is derived by integrating Eq. (13) along the overall detaching line.
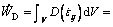
 (14)
(14)
The following section introduces the calculation of external work rate. The external loads mainly include cavity pressure, supporting pressure on the tunnel face and the gravity. Therein, the cavity pressure and supporting pressure refer to surface force, and their work rate can be expressed as
 (15)
(15)
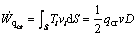 (16)
(16)
On account of the fact that the gravity is a volume force and it is always perpendicular to the motion direction of rock plug, the work rate done by gravity equals 0 throughout the failure process, namely
 (17)
(17)
Substituting Eqs. (14)–(17) into the expression of upper bound theorem (Eq. (1)), the objective function containing the detaching line f(x) can be established.
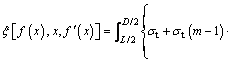
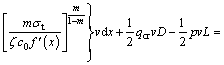
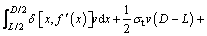
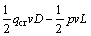 (18)
(18)
3.3 Solving of detaching curve function
The upper bound method can determine a set of solutions which are no less than the real one. The optimum upper bound solution can be obtained by optimizing the objective function. It is not difficult to find that the extreme value of objective function ξ,Eq. (18), is completely determined by the functional δ, thus the calculation of ξ is equal to that of functional δ. Based on the variational principle, it can be transformed into Eula equation, and thus the extreme problem is shifted to the solving of fixing solution of Eula equation under the boundary condition. Therein, the Eula equation of δ is
 (19)
(19)
By substituting the function δ into Eq. (19), it can be simplified as
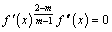 (20)
(20)
By solving this second-order differential equation, the expression of the detaching line f(x) can be derived as
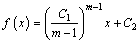 (21)
(21)
where C1 and C2 are undetermined constants. It shows from Eq. (21) that as for the plane failure mechanism of rock plug, the detaching line is straight.
3.4 Calculation of thickness of rock plug
After deriving the expression of the detaching line, an equation set including the variables (H, L, C1 and C2) can be obtained based on the geometrical relationship of the failure mode in Fig. 3(a).
 (22)
(22)
Consequently, the representation of the safe thickness of rock plug is derived as
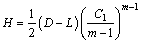 (23)
(23)
However, parameters C1 and L are variables in Eq. (23), which can be simultaneously computed according to the mechanical boundary condition and upper bound theorem. Initially, on the basis of the mechanical boundary condition, a micro-unit located in the interface of the detaching curve and the water-filled cavern is selected to conduct mechanical analysis, as shown in Fig. 4.
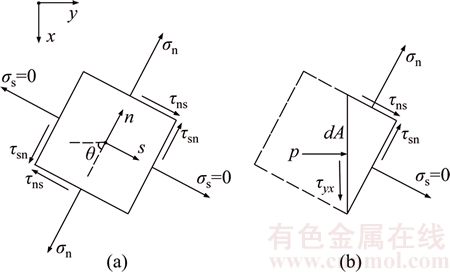
Fig. 4 Diagram of mechanical analysis of micro-unit located in detaching line (a), and on interface of detaching curve and water-filled cave (b)
According to the mechanical equilibrium equation in the vertical direction, the expression of shear stress τyz can be simplified and derived.
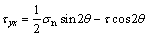 (24)
(24)
Considering the assumption of cavity pressure which is uniformly and perpendicularly distributed on the surface of karst cavern, there is no shear stress on its surface. As a consequence, τyz is equal to zero at the position of (x=L/2, y=0). Substituting Eqs. (4), (7) and (12) into Eq. (24) for simplification, the function which solely includes the parameter C1 is gained.
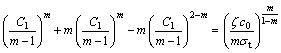 (25)
(25)
Subsequently, another function, including the undetermined parameter C1 and the scope of cave pressure L, can be obtained by equating the internal energy dissipation to the external work rate, i.e.,
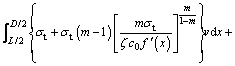
 (26)
(26)
Through integration and simplification, it results in

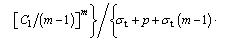
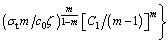 (27)
(27)
When basic parameters are determined, the values of C1 and L can be solved with Eq. (23) and Eq. (27). Then the safe thickness of rock plug can finally be derived by taking the values of C1 and L back into Eq. (22). Moreover, it can conclude from Eqs. (12), (14), (18), (25) and (27) that the appearance of nonlinear dilatancy coefficient ζ and initial cohesion c0 takes the form of product. Thus, the essential of the modification of the P-L failure criterion adopted in this paper is actually the reduction of coefficient c0.
4 Parameter sensitivity analysis
According to the deducing progress above, the parameters that influence the property of rock plug structure include: nonlinear dilatancy coefficient ζ, nonlinear coefficient m, initial cohesion c0, cavern pressure p, supporting pressure qcr and height of tunnel section D. Parameters c0, p, qcr and D can be determined by laboratory test or field measurement, and these parameters are assumed to be constant for a given tunnel condition. While as for parameters ζ and m, there does not exist a general method to determine their values at present, and they are generally determined by experience and engineering analogy in practical. Thus, this work focuses on the influences of ζ, m and their combination with other parameters on the safe thickness of rock plug. Moreover, the change of failure scope of rock plug with the variation of different parameters is also discussed.
4.1 Effects of parameters ζ and m on safe thickness of rock plug
ζ and m are the critical parameters that their values directly relate to the result of the thickness of rock plug. Therefore, in order to determine the reasonable ranges of ζ and m, this work investigates their influences at first. The values of the parameters during the analysis are: m=1.0–3.0, ζ=0.1–1.0, c0=1.0 MPa, σt=0.4 MPa, p=1.0 MPa, qcr=0.1 MPa and D=10 m. Results of the safe thickness of rock plug are illustrated in Fig. 5.

Fig. 5 Influence of parameters ζ and m on safe thickness of rock plug:
It can be seen from Fig. 5(a) that the thickness of rock plug reduces with the increase of nonlinear dilatancy coefficient. But for the section of ζ<0.2, the thickness decreases approximately in a straight line with a large amplitude of variation. For instance, when ζ increases from 0.1 to 0.2, the safe thickness decreases by nearly 8.0 m. Comparing with the thickness of rock plug generally obtained by empirical method [28], the calculation results of ζ<0.2 section are distorted. Therefore, in order to ensure reasonable results, it is suggested that the value of ζ should be between 0.2 and 1.0 with respect to the modification method adopted in this work.
The nonlinear coefficient m has great influence on the thickness of rock plug as well. With the increase of m, the safe thickness gradually increases. Then, when m reaches about 2.0, the curves in Fig. 5(b) become relatively smooth, which means that m has a little influence on the safe thickness. Thus, the value of m is suggested to be about 2.0 in the analysis. It can meet the accuracy requirements.
Moreover, it can also be found from Fig. 5(a) that interactions exist between ζ and m, which means that m has greater influence on safe thickness with the value of ζ being larger. For example, the difference of safe thickness between m=1.0 and m=2.0 is about 0.6 m when ζ=0.2, while it increases to about 1.0 m when ζ=1.0.
4.2 Effects of combinations of m with other parameters on safe thickness
In order to investigate the influences of combinations of nonlinear coefficient m with other parameters (including c0, p, qcr and D), the values of different parameters are: m=1.5–2.5, ζ=0.6, c0=0.5–3.0 MPa, σt=0.4 MPa, p=0.5–3.0 MPa, qcr=0–0.8 MPa and D=5–15 m. Results of safe thickness of rock plug are illustrated in Fig. 6.
It can be seen from Fig. 6 that different parameter combinations result in different variation of the rock plug thickness. With the increase of c0 and qcr, the safe thickness decreases. However, with the increase of p and D, the safe thickness increases. There also exist obvious difference of variation trend, namely, the safe thickness of rock plug shows nonlinear relation with c0 and p and linear relation with qcr and D. Moreover, the variation of m has a greater impact on the safe thickness for the case of larger values of c0, p and D or small value of qcr.
4.3 Effects of combinations of ζ with other parameters on safe thickness
The coefficients m and ζ have different meanings; m represents the bending degree of P-L failure criterion while ζ means the strength reduction of this criterion. Therefore, it is necessary to analyze the influences of combinations of ζ with other parameters on the safe thickness of rock plug separately. Excepting for m=2.0 and ζ=0.4–1.0, the values of other parameters are the same to the previous section. Results of safe thickness are illustrated in Fig. 7.
By comparing Fig. 6 with Fig. 7, it can be noted that the types of changing curve and variation law of safe thickness are similar to each other. But there still exist differences. When the value of c0 is smaller, the influence of ζ on the safe thickness is much more serious, and the influence of m shows the opposite situation.
4.4 Effects of different parameters on failure scope
The parameters mentioned above (including m, ζ, c0, p, qcr and D) do not only have influence on the safe thickness of rock plug, but also affect the failure scope. In order to clearly reflect the variation of failure scope with respect to different parameters, 18 sets of representative data are selected. According to the detaching curve equation (Eq. (21)), failure scopes of rock plug are calculated, as illustrated in Fig. 8.
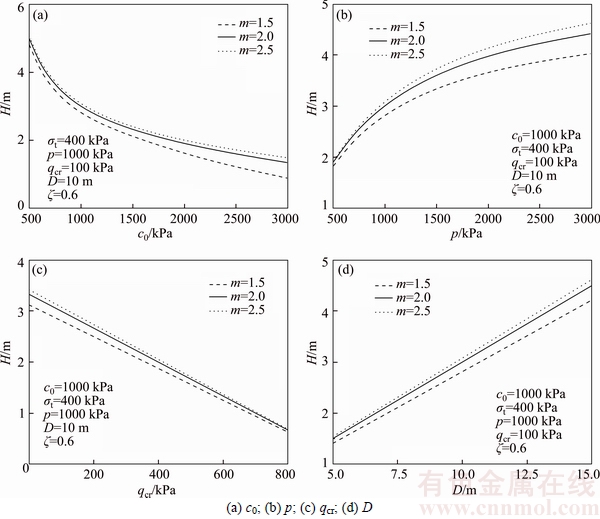
Fig. 6 Change curves of safe thickness with respect to different combinations of m with other parameters:
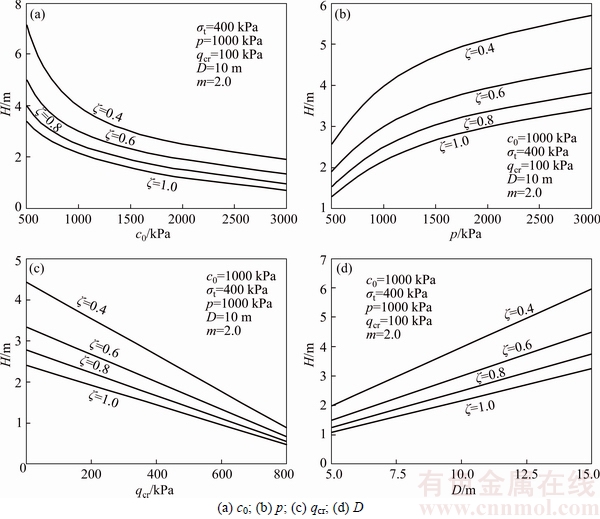
Fig. 7 Change curves of safe thickness with respect to different combinations of ζ with other parameters:
In Fig. 8, the two-dimensional failure scope of rock plug is a trapezoid with the tunnel face being its base. Similar variation regulation to the safe thickness of rock plug is found in these plots. The failure scope increases with the increasing of m, p and D, while it decreases with the increasing of c0, ζ and qcr.
The failure scope not only reflects the variation regulations of size and thickness of rock plug, but also represents the acting range of cavity pressure L and the variation of the gradient in detaching curve. L is a crucial factor which affects the failure scope of rock plug and its variation regulation is significantly different from that of safe thickness. Except for parameter p, the increase of m, ζ, c0, qcr and D results in the increase of L.
However, as for the gradient of detaching curve, the influence of different parameters is diverse. It can be seen from Figs. 8(d)–(f) that the contours of failure scope are parallel to each other with the variation of p, qcr and D, which means these three parameters have no influence on the gradient of detaching curve. Figures 8(b)–(c) indicate that the gradient of detaching curve decreases with the increasing of ζ and c0. Moreover, their variation trends are the same, and this proves again that the essential of the method adopted in this work is the modification of c0 to certain degree. However, in Fig. 8(a), the contours of failure scope intersect with the variation of m, which is obviously different from other parameters. This is because with the increase of m, the gradient of detaching curve and the value of L increase simultaneously.

Fig. 8 Failure scopes of rock plug with respect to different parameters:
5 Engineering project application
Yunwushan tunnel, located in Enshi, Hubei province of China, passes through the strata of limestone and mud dolomite [28]. The geological structure of the construction zone is rather complicated with serious faults and rich underground rivers. On 12th, October 2008, the line II of Yunwushan tunnel suffered from ‘526 karst cavern’, which is a filled-type cavern with a large amount of mud and water fillings. To prevent the occurrence of water inrush and mud outburst, a safe rock plug with 2.5–4.5 m thickness is reserved and a drainage system is constructed to reduce cavern pressure. This part uses the project to verify the validity of the proposed method.
The height of tunnel profile is 9.8 m, and the cavern pressure is 0.8 MPa. Meanwhile, it was ascertained that there exists an initial fractured zone with 1.5 m thickness around the cavern. The values of cohesion and tensile strength are 2.206 MPa and 4.147 MPa according to the laboratory test results of limestone samples collected from construction area. The numerical results of the safe thickness of rock plug are obtained for Yunwushan tunnel, shown in Table 1.
Table 1 Numerical results of safe thickness for Yunwushan tunnel with respect to different values of ζ and m

It can be seen from Table 1 that when ζ varies from 0.2 to 1.0 and m varies from 1.0 to 2.0, the calculation result of the safe thickness of rock plug ranges between 2.02 to 5.03 m. It is close to the values of practical engineering, namely 2.5–4.5 m. This good agreement validates the method proposed in this work. Moreover, it needs to indicate that the safe thicknesses listed in Table 1 are the final results which contain the thickness of the initial fracture zone.
6 Conclusions
1) In view of the reserved thickness of rock plug with the presence of a high-pressure water-rich cavern right in front of tunnel face, the nonlinear and non-associated properties of geotechnical materials are introduced into the analysis by modifying the failure criterion. Based on the two-dimensional symmetrical failure mode constructed in this work, upper bound analysis of the safe thickness is performed. Moreover, the equation of detaching curve and calculation formula of safe thick of rock plug are finally obtained. The detaching curve is linear in the two-dimensional case. The essential of the modification of P-L failure criterion is the strength reduction of initial cohesion c0.
2) The influences of ζ, m and other parameters on the safe thickness are analyzed. The results show that with the increase of ζ, c0 and qcr, the safe thickness of rock plug decreases, but parameters m, p and D have an inverse effect on the protective thickness.
3) The influences of different parameters on the failure scope of rock plug are investigated. The results show that the two-dimensional failure scope is a trapezoid, and similar variation regulation has been found in studying the thickness of rock plug.
References
[1] LIU Chao-qun, PENG Hong-jun. Analysis of the safe distance between a tunnel face and karst cave [J]. Modern Tunnelling Technology, 2012, 49(3): 109–113. (in Chinese)
[2] WU Q, WANG M, WU X. Investigations of groundwater bursting into mine seam floors from fault zones [J]. International Journal of Rock Mechanics and Ming Sciences, 2004, 41(4): 557–571.
[3] LI Li-ping, LI Shu-cai, ZHANG Qing-song. Study of mechanism of water inrush induced by hydraulic fracturing in karst tunnels [J]. Rock and Soil Mechanics, 2010, 31(2): 523–528. (in Chinese)
[4] MEGUID M A, DAND H K. The effect of erosion voids on existing tunnel linings [J]. Tunneling and Underground Space Technology, 2008, 4(2): 1–9.
[5] YANG X L, LI Z W. Factor of safety of three-dimensional stepped slope [J]. International Journal of Geomechanics, 2018, 18, DOI: 10.1061/(ASCE)GM.1943-5622.0001154.
[6] YANG X L, YAO C. Stability of tunnel roof in nonhomogeneous soils [J]. International Journal of Geomechanics, 2018, 18, DOI: 10.1061/(ASCE)GM.1943-5622.0001104.
[7] LI T Z, YANG X L. Risk assessment model for water and mud inrush in deep and long tunnels based on normal grey cloud clustering method [J]. KSCE Journal of Civil Engineering, 2018, 22, DOI: 10.1007/s12205-017-0553-6.
[8] XU J S, YANG X L. Effects of seismic force and pore water pressure on three dimensional slope stability in nonhomogeneous and anisotropic soil [J]. KSCE Journal of Civil Engineering, 2018, 22, DOI: 10.1007/s12205-017-1958-y.
[9] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek–Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665–673.
[10] PAN Q,DIAS D. Face stability analysis for a shield-driven tunnel in anisotropic and nonhomogeneous soils by the kinematical approach [J]. International Journal of Geomechanics, 2016, 16(3): 04015076.
[11] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material [J]. Geotechnique, 1990, 40(4): 581–606.
[12] SOUBRA A H. Three-dimensional face stability analysis of shallow circular tunnels[C]// International Society for Rock Mechanics. Melbourne: CRC, 2000: 19–24.
[13] YANG X L. Lower bound analytical solution for bearing capacity factor using modified Hoek–Brown failure criterion [J]. Canadian Geotechnical Journal, 2018, 55, DOI: 10.1139/cgj-2016-0694.
[14] YANG X L. Effect of pore-water pressure on 3D stability of rock slope [J]. International Journal of Geomechanics, 2017, 17(9): 06017015.
[15] YANG X L, ZHANG R. Limit analysis of stability of twin shallow tunnels considering surface settlement [J]. KSCE Journal of Civil Engineering, 2018, 22, DOI: 10.1007/s12205-017-1398-8.
[16] XU J S, PAN Q J, YANG X L, LI W T. Stability charts for rock slopes subjected to water drawdown based on the modified nonlinear Hoek-Brown failure criterion [J]. International Journal of Geomechanics, 2018, 18(1): 04017133.
[17] YIN J H, WANG Y J, SELVADURAI A P. Influence of non- associativity on the bearing capacity of a strip footing [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(11): 985–989.
[18] LUO W H, LI W T. Reliability analysis of supporting pressure in tunnels based on three-dimensional failure mechanism [J]. Journal of Central South University, 2016, 23(5): 1243–1252.
[19] YANG X L, LI Z W, LIU Z A, XIAO H B. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media [J]. Journal of Central South University, 2017, 24(4): 957–966.
[20] YANG X L, ZHANG R. Collapse analysis of shallow tunnel subjected to seepage in layered soils considering joined effects of settlement and dilation [J]. Geomechanics and Engineering, 2017, 13(2): 217–235.
[21] AGAR J G, MORGENSTERN N R, SCUT J D. Shear strength and stress-strain behaviour of Athabasca oil sand at elevated temperatures and pressures [J]. Canadian Geotechnical Journal, 1987, 24(1): 1–11.
[22] LUQUE R F, MANDL G. Fully Developed Plastic Shear Flow of Granular Materials [J]. Géotechnique, 1970, 20(3): 277–307
[23] DRESCHER A, DRTOURNAY E. Limit load in translational failure mechanisms for associative and non-associative materials [J]. Géotechnique, 1993, 43(3): 443–456.
[24] LI T Z, YANG X L. Reliability analysis of tunnel face in broken soft rocks using improved response surface method [J]. International Journal of Geomechanics, 2018, 18, DOI: 10.1061/ (ASCE)GM.1943-5622.0001129.
[25] LI T Z, LI Y X, YANG X L. Rock burst prediction based on genetic algorithms and extreme learning machine [J]. Journal of Central South University, 2017, 24(9): 2105–2113.
[26] LI T Z, YANG X L. Limit analysis of failure mechanism of tunnel roof collapse considering variable detaching velocity along yield surface [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 100: 229–237.
[27] PESENDORFER M, LOEW S. Subsurface exploration and transient pressure testing from a deep tunnel in fractured and karstified limestones [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(1):121-137.
[28] GUO Jia-qi. Study on against-inrush thickness and water-burst mechanism of karst tunnel [D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese)
(Edited by HE Yun-bin)
Cite this article as: YANG Zi-han, ZHANG Rui, XU Jing-shu, YANG Xiao-li. Energy analysis of rock plug thickness in karst tunnels based on non-associated flow rule and nonlinear failure criterion [J]. Journal of Central South University, 2017, 24(12): 2940–2950. DOI:https://doi.org/10.1007/s11771-017-3708-1.
Foundation item: Project(2013CB036004) supported by the National Basic Research Program of China; Projects(51378510, 51308072) supported by National Natural Science Foundation of China; Project(CX2014B069) supported by the Hunan Provincial Innovation Foundation for Postgraduate, China
Received date: 2016-03-16; Accepted date: 2016-05-23
Corresponding author: XU Jing-shu, PhD; Tel: +86–15207499204; E-mail: csushdxjs@csu.edu.cn

