碟式太阳能聚光器风载仿真
王曙辉,王红,余明果,龚金科,颜胜
(湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082)
摘要:为研究风载荷对碟式太阳能聚光器的影响,基于CFD流体动力学分析软件,建立碟式太阳能聚光器风载仿真计算模型,分析聚光器风载作用下的流场,计算聚光器的平均风力系数和风力矩系数,并研究聚光器风力系数和风力矩系数随不同方位角和高度角的变化规律。研究结果对开发碟式太阳能聚光器、优化聚光器的避风控制策略,以及提高太阳能电站风灾害的抵抗能力具有重要的参考意义。
关键词:碟式太阳能聚光器;仿真;风力系数;风力矩系数
中图分类号:TK514 文献标志码:A 文章编号:1672-7207(2014)12-4415-07
Simulation of wind load on dish solar condenser
WANG Shuhui, WANG Hong, YU Mingguo, GONG Jinke, YAN Sheng
(State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,
Hunan University, Changsha 410082, China)
Abstract: In order to study the influence of wind loads on dish solar condenser, a simulation model of the dish solar condenser was established under wind loads based on CFD fluid dynamics analysis software. The flow field of the condenser under wind load was analyzed, and the average wind load coefficients and wind torque coefficients were calculated. In addition, the variations of wind load coefficients and wind torque coefficients with different azimuth angles and altitude angles were investigated. The results have great reference significance to the development of dish solar condenser, optimizing the condenser sheltered control strategy and improving the resistance of the solar power station wind damage.
Key words: dish solar condenser; simulation; wind load coefficients; wind torque coefficients
随着石化燃料的大量消耗,环境污染与能源短缺问题日益严重,寻找替代性的清洁能源、维持人类的可持续发展已经成为各国共同的努力目标。太阳能因其储量无限性、分布普遍性、利用清洁性及经济性等特征被认为是未来人类最为重要的能源之一[1-3]。相对于光伏发电来说,太阳能热发电具有电力品质好、调节性强以及可实现全天候供电等特点,成为目前太阳能开发利用的研究热点[4]。为了提高发电效率,无论哪种形式的光热发电技术,都需要通过聚光设施将能量分布密度较低的太阳能进行汇聚以提高热机工质温度,进而提高热机的效率。作为光热发电聚光设施的一种,碟式聚光器可实现对太阳的二维即时跟踪,可与斯特林发动机、小型蒸汽轮机或小型燃气轮机等热机组成单独的发电系统,是一个十分具有发展前景的研究方向[5-6]。对于碟式聚光器的开发来说,风载荷是必须考虑的因素。聚光器在对太阳进行跟踪的过程中,其姿势在不停地变化,同时风速、风向可能也在变化,相应地,聚光器所受到的风载荷也会发生变化[7-9]。在风载荷的作用下,可能导致聚光器的实际方向偏离理论位置而改变反射面聚焦位置或反射面的形状改变而造成焦斑能量分布特性变化,恶化聚光器与吸热器之间的匹配关系,降低吸热器对太阳能的吸收效率,影响发电系统的效率、寿命和可靠性,甚至更为严重的是,过大的风载可能导致整个碟式太阳能发电系统损毁,给太阳能电站造成巨大的损失[10-11],所以研究碟式聚光器的风载荷对碟式太阳能热发电装配的研制具有重要意义。目前,对碟式聚光器进行风载荷系统研究的文献不多。对太阳能聚光器等设施所受风载的研究一般可采用风洞实验法和数值仿真法[12]。通过风洞进行试验研究的方式成本高昂、周期长,且不易直观地揭示风与结构之间的相互耦合关系。随着计算机技术的快速发展及计算方法的逐渐成熟,采用数值仿真研究物体所受的风载荷逐渐成为可能,数值仿真分析方法在碟式雷达天线的风载研究领域已经取得了较好的进展[13-14]。其中包括对雷达天线结构设计时所考虑的风力的计算和结构优化以及对天线的数值模拟过程和计算方法[15-19]。将数值法应用于大型太阳能聚光器的研究还比较少,卢春玲等[15-16]使用风洞实验法对太阳能定日镜的体型系数进行研究以实现对定日镜结构的抗风设计和定日镜受风作用时的风振响应的分析[20-21]。本文作者基于数值仿真技术对碟式太阳能聚光器在不同姿势下的风载进行了比较系统的研究。建立了碟式太阳能聚光器风载仿真模型,分析了聚光器的流场分布,得到了碟式聚光器不同姿势下的风载系数及其随高度角和方位角的变化规律。研究结果可为开发碟式太阳能聚光器提供参考依据,也可为制定碟式太阳能热发电装备的控制策略,尤其是避风控制策略提供依据。
1 聚光器风载荷定义
根据力学原理,对于作用在反射面的风力,如果向某一点简化,可以简化为一个合力和力偶。
风力F与空气密度ρ、流速v、流体的黏性μ、物体的主要尺寸D有关,可表达为
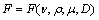 (1)
(1)
用量纲分析法可得[17]:
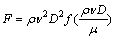 (2)
(2)
式中:D2与物体的特征面积A成正比,对于碟式聚光器来说,A为开口面积,即聚光器的采光面积;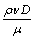 为雷诺数Re,是判断流动状态的参数。于是式(2)可表示为
为雷诺数Re,是判断流动状态的参数。于是式(2)可表示为
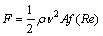 (3)
(3)
令CF=f(Re),称为风力系数,它与物体的形状和雷诺数Re有关,又称为形状系数。于是式(3)可表示为
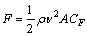 (4)
(4)
对于非对称物体来说,当风向不同时,风力也不同,相应的,风力系数也在变化。
取风向为-x方向,垂直向上为z方向,与x和z同时垂直的方向为y方向,则当碟式聚光器处于空间的某个姿势下,其受到x,y和z方向的风力分别为
 (5)
(5)
 (6)
(6)
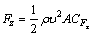 (7)
(7)
式(5)~(7)中,定义 ,
, 和
和 分别为阻力系数、侧力系数、升力系数。
分别为阻力系数、侧力系数、升力系数。
由于聚光器在风的方向上时非对称的,所以还会还会产生风力矩,可表示为
 (8)
(8)
式中:CM为风力矩系数;L为当量合力点至聚光器定义的转轴之间的垂直距离。
则式(8)在x,y和z 3个方向的力矩为
 (9)
(9)
 (10)
(10)
 (11)
(11)
式中: ,
,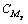 和
和 分别为聚光器的翻滚力矩系数、俯仰力矩系数和方位力矩系数;Lx,Ly和Lz分别为所受风力当量合力点至x,y和z 3个方向的回转半径。各载荷定义如图1所示。
分别为聚光器的翻滚力矩系数、俯仰力矩系数和方位力矩系数;Lx,Ly和Lz分别为所受风力当量合力点至x,y和z 3个方向的回转半径。各载荷定义如图1所示。

图1 碟式太阳能聚光器风力及风力矩示意图
Fig. 1 Sketch of wind loads and wind torques on dish solar condenser
2 聚光器物理模型
太阳能聚光器处于大气边界层中,当风对聚光器绕流时,相当于该聚光器处于完全开口的流动风场中。风对聚光器作用的影响具有一定的范围,因此在数值模拟时需给定一定的三维计算区域且给定和实际中相对应的边界条件。过大的流体区域意味着过大的网格数量,计算量会比较大,计算时间较长,而流体区域过小,则流动发展不充分,容易引起计算结果的失真。所以划定合适的流体计算区域对减少计算时间和保证计算精度很重要[22]。此聚光器模型的直径D为17.5 m,厚度H为0.03 m。为了简化计算,可以将反射面后侧的支撑网架对流场的影响不予考虑,反射面由216块反射镜组成,任意相邻的两块反射镜之间留有15 mm的缝隙。为保证气流在流体域内的流动达到充分发展的状态,经过多次建模仿真,确定流体域的尺寸(长×宽×高)为:170 m×80 m×80 m,模型中心距地面高度为15 m,风的入口距模型中心距离为55 m。
2.1 网格划分
对该模型的流体区域采用的是多面体网格,多面体网格具有很好的灵活性和适应性,易于进行网格自适应。图2所示为碟式太阳能聚光器的仿真模型。对整个流域的网格进行划分时采用逐级划分方式,远离聚光器的区域由远及近逐步加密,且对模型表面网格进行细化。
2.2 边界条件
对该计算流体而言,假定气流为不可压缩的定常流动,并且不考虑地面实际形状和粗糙度的影响,各边界条件选取如下。

图2 碟式太阳能聚光器物理模型
Fig. 2 Physical model of dish solar condenser
1) 入口边界条件:采用速度入口边界条件,入口风为均布定常风。
2) 出口边界条件:采用完全发展出流边界条件。
3) 自由流边界条件:流体域的顶部和左右两侧设置为自由流边界。
4) 壁面条件:聚光器表面和计算域底部采用无滑移的壁面条件。
2.3 湍流模型
采用的湍流模型为标准的κ-ε模型。标准的ε-ε模型是把用来表征涡黏性系数的湍流动能ε和湍流耗散率ε 2个特征量用相应的微分方程控制。
在标准的κ-ε模型中,当为不可压缩流动且不考虑浮力等因素时,对应的2个未知量κ和ε的输运方程为

 (12)
(12)

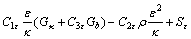 (13)
(13)
式中: 为由平均速度梯度引起的湍动能κ的产生项;Gb为由于浮力引起的湍动能κ的产生项,对于不可压缩流体Gb=0;YM代表湍流中脉动扩张的贡献,对于不可压缩流体YM=0;C1ε,C2ε和C3ε均为经验常数,σκ和σε分别为湍动能κ和湍流耗散率ε对应的Prandtl数,根据Launder等的推荐值及后来的试验验证[23],模型常数取值如下:
为由平均速度梯度引起的湍动能κ的产生项;Gb为由于浮力引起的湍动能κ的产生项,对于不可压缩流体Gb=0;YM代表湍流中脉动扩张的贡献,对于不可压缩流体YM=0;C1ε,C2ε和C3ε均为经验常数,σκ和σε分别为湍动能κ和湍流耗散率ε对应的Prandtl数,根据Launder等的推荐值及后来的试验验证[23],模型常数取值如下:
C1ε=1.44,C2ε=1.92,C3ε=0,σκ=1.0,σε=1.3
3 仿真结果分析
3.1 流场分布特征
由于太阳能聚光器在风流动过程中起障碍物作用,会造成气流的局部扰动,引起压力场和速度场的变化而致使发生空气动力学的畸变,最终使其周围的流场变得复杂化。
图3所示为聚光器在高度角为0o、方位角为0o,即风向与聚光器开口的法线方向平行时,风绕过聚光器时的气流流动情况。由图3可知:由于聚光器的阻碍作用,风速在接近天线时急剧减小,流动气体向聚光器边缘挤压导致流速增大,流体在聚光器前缘分离,并在聚光器后部形成范围较广的尾流区,其中流动方向相反的2个涡消耗了大量的动能,在聚光器后部形成负压区。

图3 聚光器周围流场的分布
Fig. 3 Distributions of flow field around condenser
3.2 不同角度时聚光器的风力系数
通过式(4)可以看出:只要知道风力系数CF就可以计算风力。于是对结构风力的计算,就可以转化为确定风力系数CF。风力系数CF只与物体形状和雷诺数Re有关,对于流线型物体或半流线型物体风力系数与雷诺数Re有关,而对于非流线型物体,在一般情况下,风力系数不随雷诺数Re而变,非流线型结构的体型系数仅和结构的形状有关[17]。对于本文中所涉及的太阳能聚光器结构为非流线型物体,所以不考虑雷诺数Re的影响。因此对于同样形状的所有物体,只要知道了该形状物体的风力系数CF,就可以对同样形状的所有物体进行风力计算了。
风力系数的计算公式为
 (13)
(13)
在后处理中创建定量表格,可以得到高度角0o,方位角0o时的风阻力的计算结果为Fx=97 129 N,由式(13)求得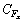 =1.843,这在文献[17]中的抛物面风阻力系数的范围内。因此可以认为此模型的建模、网格划分和计算方法是正确的。
=1.843,这在文献[17]中的抛物面风阻力系数的范围内。因此可以认为此模型的建模、网格划分和计算方法是正确的。
3.2.1 阻力系数
图4所示为太阳能聚光器不同高度角时阻力系数随方位角的变化规律。由图4可知:聚光器高度角为90°时,阻力系数不随方位角的变化而变化;其他高度角时,随着方位角的增大,阻力系数先增大后减小,方位角在接近90°工作位置时,模型的阻力系数最小,表明在此时风阻力最小,聚光器方位角为0°时,阻力系数最大即阻力最大,这主要是因为阻力方向的有效迎风面积在不断变化的缘故。聚光器方位角相同时,阻力系数随着高度角的增大而减小。

图4 不同高度角时阻力系数随方位角的变化规律
Fig. 4 Variations of resistance coefficient with azimuth angle under different altitude angles
3.2.2 侧力系数
图5所示为太阳能聚光器不同高角度时侧力系数随方位角的变化规律。由图5可知:聚光器高度角为90°时,侧力系数的绝对值很小且不随方位角的变化而变化,此时侧力很小;其他高度角时,方位角为0°和180°时,聚光器测力系数绝对值很小,接近于0,表明此时聚光器所受侧力很小,方位角在接近90°左右时,侧力系数绝对值最大,即聚光器侧力最大。聚光器方位角相同时,侧力系数的绝对值随高度角的增大而减小。
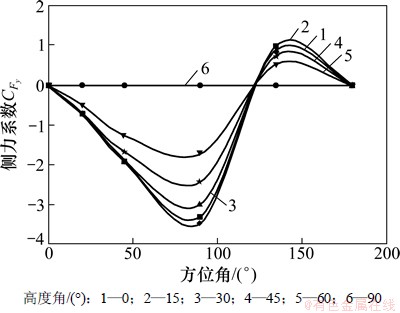
图5 不同高度角时侧力系数随方位角的变化规律
Fig. 5 Variations of lateral force coefficient with azimuth angle under different altitude angles
3.2.3 升力系数
图6所示为太阳能聚光器不同高度角时升力系数随方位角的变化规律。由图6可知:聚光器高度角为90°时,升力系数的绝对值最大且不随方位角的变化而变化,此时升力绝对值最大;其他高度角时,方位角为0°和180°时,聚光器升力系数绝对值最小,方位角在接近90°时升力系数的绝对值最大,即升力最大。聚光器方位角相同时,升力系数的绝对值随高度角的增大而增大。
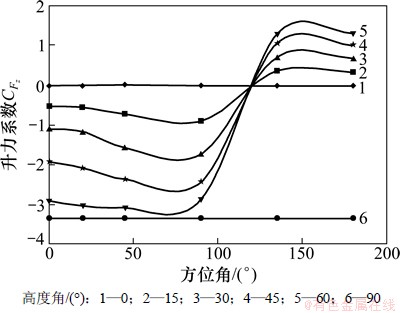
图6 不同高度角时升力系数随方位角的变化规律
Fig. 6 Variations of lift coefficient with azimuth angle under different altitude angles
3.2.4 翻滚力矩系数
图7所示为太阳能聚光器不同高角度时翻滚力矩系数随方位角的变化规律。由图7可知:聚光器翻滚力矩系数与其他力系数和力矩系数相比数值较小且变化情况比较复杂。高度角为90°时,聚光器翻滚力矩系数的绝对值接近于0,此时翻滚力矩很小;其他高度角时,方位角为0°和180°时,翻滚力矩系数绝对值接近于0,此时翻滚力矩很小。聚光器在高度角为15°,方位角为45°左右时翻滚力矩系数最大,此时聚翻滚力矩最大。

图7 不同高度角时翻滚力矩系数随方位角的变化规律
Fig. 7 Variations of roll moment coefficient with azimuth angle under different altitude angle
3.2.5 俯仰力矩系数
图8所示为太阳能聚光器不同高角度时俯仰力矩系数随方位角的变化规律。由图8可知:聚光器高度角为90°时,俯仰力矩系数的绝对值最大且不随方位角的变化而变化,此时俯仰力矩的绝对值最大。其他高度角时,聚光器方位角为90°左右时,俯仰力矩系数的绝对值最大,此时俯仰力矩绝对值最大。聚光器方位角相同时,聚光器俯仰力矩系数的绝对值随高度角的增大而增大,聚光器受风力作用时高度角越大其所受俯仰力矩越大。

图8 不同高度角时俯仰力矩系数随方位角的变化规律
Fig. 8 Variations of pitch moment coefficient with azimuth angle under different altitude angles
3.2.6 方位力矩系数
图9所示为太阳能聚光器不同高角度时方位力矩系数随方位角的变化规律。由图9可知:聚光器高度角为90°时,方位力矩系数很小且不随方位角的变化而变化,此时方位力矩很小;其他高度角时,聚光器方位角在90°左右时,方位力矩系数最大,此时聚光器所受方位力矩最大,方位角在0°和180°时,方位力矩系数绝对值很小,接近于0,此时聚光器方位力矩很小。聚光器方位角相同时,方位力矩系数绝对值随高度角的增大而减小。

图9 不同高度角时方位力矩系数随方位角的变化规律
Fig. 9 Variations of orientation moment coefficient with azimuth angle under different altitude angles
4 结论
1) 碟式太阳能聚光器在高度角为90o,即聚光器开口向上时,阻力系数、侧力系数、翻滚力矩系数以及方位力矩系数都获得最小值,且不受风向的影响,是晚间避风的最佳姿势;
2) 在同样的方位角下,阻力系数及侧力系数的绝对值都随着高度角的增加而减小,而升力系数的绝对值随高度角的增加而增加;
3) 高度角小于90°时,俯仰力矩系数和方位力矩系数随方位角的变化规律相同。方位角相同时,聚光器俯仰力矩系数的绝对值随高度角的增大而增大,方位力矩系数绝对值随高度角的增大而减小。而翻滚力矩系数则在高度角为15°,方位角为45°左右时达到最大,这也是聚光器受力最为恶劣的姿势,聚光器关键受力部位设计时,应该重点关注该姿势下的载荷。
参考文献:
[1] 钱伯章. 新能源[M]. 北京: 化学工业出版社, 2007: 8-125.
QIAN Bozhang. New enery[M]. Beijing: Chemical Industry Press, 2007: 8-125.
[2] 中国科学院能源战略研究组. 中国能源可持续发展战略专题研究[M]. 北京: 科学出版社, 2006: 1-414.
Energy strategy study group of the Chinese Academy of Sciences. China Sustainable Energy Development Strategy case studies[M]. Beijing: Science Press, 2006: 1-414.
[3] 孙妍. 中国太阳能产业发展政策现状、问题和对策[D]. 北京: 华北电力大学, 2011: 1-42.
SUN Yan. Chinese solar industry development policy status,problems and countermeasures[D]. Beijing: North China Electric Power University, 2011: 1-42.
[4] 李鑫, 李安定, 李斌, 等. 碟式斯特林太阳能热发电系统经济性分析[J]. 中国电机工程学报, 2005, 25(12): 108-111.
LI Xin, LI Anding, LI Bin, et al. Economic analysis of dish stirling solar power system[J]. Proceedings of the Chinese Society for Electrical Engineering, 2005, 25(12): 108-111.
[5] 廖葵, 龙新峰. 碟式太阳能热发电系统中吸热器温度场模拟[J]. 化学工程, 2009, 37(8): 63-66, 78.
LIAO Kui, LONG Xinfeng. Simulation of temperature field for heat receiver in solar-only disk power generation[J]. Chemical Engineering, 2009, 37(8): 63-66, 78.
[6] 刘巍, 王宗超. 碟式太阳能热发电系统[J]. 重庆工学院学报(自然科学版), 2009, 23(10): 99-103.
LIU Wei, WANG Zongchao. Dish-style solar thermal power generation system[J]. Journal of Chongqing Institute of Technology, 2009, 23(10): 99-103.
[7] 冯东亮. 基于CFD太阳能追日器风载仿真[D]. 武汉: 武汉理工大学,2011: 11-38.
FENG Dongliang. Simulation of wind load around the solar tracking device based on CFX[D]. Wuhan: Wuhan University of Technology, 2011: 11-38.
[8] Ulmer S,Reinalter W,Heller P,et al. Beam characterization and improvement with a flux mapping system for dish concentrators[J]. Journal of Solar Energy Engineering, 124(2), 182-188.
[9] Holmes J D. Effective static load distributions in wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(2): 91-109.
[10] Quinn A D, Baker C J, Wright N G. Wind and vechicle induced forced on flat plates-Parts: Wind induced force[J]. Journal of Engineering and industrial Aerodynamics, 2001, 89(9): 817-829.
[11] Chang C. Computational fluid dynamics simulation of pedestrian wind in urban area with the effects of tree[J]. Wind and Structures, 2006, 9(2): 147-158.
[12] Baker C J. Wind engineering-past,present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 843-870.
[13] Farid C C. Numerical modeling of wind and dust patterns around a full-scale paraboloidal solar dish[J]. Renewable Energy, 2012, 39(1): 356-366.
[14] McBean R P. Wind load effects on flat plate solar collectors[J]. Journal of Structural Engineering, 1985, 111(2): 343-352.
[15] 杜强, 杜平安. 天线风载的数值模拟分析[J]. 现代雷达, 2009, 31(3):77-80.
DU Qiang, DU Pingan. Analysis for numerical simulation of wind load on antenna[J]. Modern Radar, 2009, 31(3): 77-80.
[16] 帅永, 张晓峰, 谈和平, 等. 抛物面式太阳能聚能系统聚光特性模拟[J]. 工程热物理学报, 2006, 27(3): 484-486.
SHUAI Yong, ZHANG Xiaofeng, TAN Heping, et al. Simulation for concentrating characteristic of parabolic solar collector system[J]. Journal of Engineering Thermophysics, 2006, 27(3): 484-486.
[17] Finardi S, Tinarelli G, Faffian P, et al. Evaluation of different wind field modeling techniques for wind energy applications over complex topography[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 283-294.
[18] Leitl B M, Kastner-Klein P, Rau M, et al. Concentration and flow distributions in the vicinity of U-shaped buildings: Wind-tunnel and computational data[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67/68: 745-755.
[19] Peterka J A, Cermark J E. Wind pressure on buildings probability densities[J]. ASCE J Struct Div, 1975, 101(6): 1255-1267.
[20] 卢春玲, 李正农, 李秋胜. 风对定日镜影响的计算流体动力学数值模拟[J]. 哈尔滨: 自然灾害学报,2010,19(1):185-191.
LU Chuling, LI Zhengnong, LI Qiusheng. Numerical simulation of wind effects on heliostat by computational fluid dynamics[J]. Haerbin: Journal of Natural Disasters, 2010, 19(1): 185-191.
[21] 宫博, 李正农, 王莺歌. 太阳能定日镜结构风载体型系数风洞试验研究[J]. 湖南大学学报(自然科学版),2008, 35(9):6-9.
GONG Bo, LI Zhengnong, WANG Yingge. Wind tunnel test study on the wind load shape coefficient of heliostat[J]. Journal of Hunan University(Natural Sciences), 2008, 35(9): 6-9.
[22] 叶尚辉, 李天贵. 天线结构设计[M]. 西安: 西北电讯工程学院出版社, 1986: 83-110.
YE Shanghui, LI Tiangui. Design for antenna structure[M]. Xian: Northwest Telecommunication Engineering College Press, 1986: 83-110.
[23] 王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2005: 113-141.
WANG Fujun. Analysis for computational fluid dynamics[M]. Beijing: Tshinghua University Press, 2005: 113-141.
(编辑 陈爱华)
收稿日期:2014-02-20;修回日期:2014-06-17
基金项目:汽车车身先进设计制造国家重点实验室自主研究项目(61075002)(Project (61075002) supported by Independent Research Project of State Key Laboratory of Advanced Design and Manufacture for Vehicle Body)
通信作者:王曙辉(1976-),男,甘肃天水人,讲师,博士,从事汽车发动机排放控制新技术、新能源技术研究;电话:13974991209;E-mail:wangshh507@163.com