DOI: 10.11817/j.issn.1672-7207.2017.04.015
基于刚度链的纯电动汽车车身主断面优化设计
刘保公,刘子建,周小龙,刘瑜
(湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082)
摘要:基于梁单元车身简化几何模型建立以主断面为节点的车身静态和动态刚度链数学模型,研究电动车车身主断面属性与刚度以及模态的关系;以车身刚度、模态为约束条件,以车身质量最小为目标函数进行多目标优化,并利用遗传算法求解,得到同时满足静态刚度和频率特性要求的电动汽车车身主断面属性参数。建立对应的车身骨架有限元模型计算刚度及模态,并与刚度链优化结果进行对比分析。对比分析结果验证了本文研究方法的合理性和有效性。
关键词:车身主断面;车身刚度链;静态刚度;模态分析;多目标优化设计
中图分类号:U463.82 文献标志码:A 文章编号:1672-7207(2017)04-0959-09
Main section optimization design of pure electric car body based on stiffness chain
LIU Baogong, LIU Zijian, ZHOU Xiaolong, LIU Yu
(State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,
Hunan University, Changsha 410082, China)
Abstract: A mathematical model of both static and dynamic stiffness chain of vehicle body based on the beam element simplified geometric model was built, which considered main sections as nodes and accurately described the relationships between properties of electric vehicle body main section, the stiffness and the modal. This model considered body stiffness and modal as constraint conditions and body lightweight as objective function for multi-objective optimization, and it was solved by using genetic algorithms. BIW main sections parameters of electric vehicle which meet the requirements of both static stiffness and dynamic vibration frequency were obtained. A corresponding body frame finite element model was established to calculate its stiffness and modal. The rationality and effectiveness of this method are verified by comparing with the CAE calculation results.
Key words: vehicle body main section; vehicle body stiffness chain; static stiffness; modal analysis; multi-objective optimization design
纯电动汽车(PEV)市场近几年发展迅速。目前,国内外对于纯电动汽车的研究多集中于电池管理、动力驱动以及电机控制等技术,对车身设计方法的研究仍不够深入[1-2]。由于驱动、储能装置的特殊性,直接沿用传统的车身设计技术难以满足电动汽车在刚强度、模态及疲劳寿命等方面的性能要求[3]。研究性能主导的纯电动汽车车身正向设计方法具有重要意义。近年来,国内外研究者提出一些电动车车身设计方法,如:谢伦杰等[4]采用多目标拓扑优化方法求取车身载荷传递路径,完成车身梁结构优化;张伟等[5]将拓扑优化与尺寸优化相结合进行电动车车身轻量化设计;NORBEG等[6]利用拓扑优化方法得到车身前部梁结构布置形式,保证了车身良好的舒适性和操纵性;QUINN[7]以车身刚度性能为主导,综合考虑汽车多种静载工况,得到了白车身合理的材料分布(白车身指完成焊接但未涂装之前的车身,不包括回门两盖等运动件)。这些研究表明了拓扑优化和尺寸优化方法在电动车车身概念设计中的有效性,在获得车身质量良好分布的同时,提出的主断面属性参数的求取方法却缺少代表性。田海豹[8]提出用静态刚度链方法设计燃油车白车身,优化了车身主断面的材料分布,但没有考虑车身的动态特性,得到的主断面属性参数精度有待提高。为此,本文作者综合考虑电动车白车身动态和静态特性,以车身主断面属性为优化变量,建立车身刚度链模型,利用多目标遗传算法,以车身质量最小为目标函数,车身弯曲刚度、模态频率为约束,实现电动车车身主断面参数的多目标优化,并通过有限元分析模型验证研究方法的有效性。
1 电动汽车车身简化几何模型
下面以某款双人座微型电动汽车为例,介绍适用于电动车车身结构概念设计的刚度链设计方法。整车基本参数如表1所示。
表1 整车基本参数
Table 1 Basic parameters of vehicle

电动车车身概念设计依据整车总布置参数以及性能指标进行,其他信息的不确定程度高,需要建立如图1所示的车身概念设计空间模型。为了便于分析,将整车分为左侧围系统、右侧围系统、底钣系统、顶盖系统等几部分。依据构成关系和设计要求,以两前车轮轴中心点为原点、X轴水平向后、Y轴垂直向上建立整车设计坐标系S0。进一步建立梁单元表示的车身结构简化几何模型,如图2所示。
依据车身设计方案确定1/2车身的18个主断面的具体位置(如图2所示)。主断面与所属结构件的对应关系如表2所示。

图1 车身概念设计空间
Fig. 1 Body conceptual design space

图2 车身简化几何模型
Fig. 2 Body simplified model
表2 主断面与结构件对应关系
Table 2 Main sections and corresponding relationship with structure

2 基于车身刚度链的主断面优化设计
本文采用的车身刚度链设计方法以车身简化几何模型表示车身结构拓扑关系,以结构力学、梁单元法和传递矩阵法建立车身整体刚度与局部刚度之间的关系,是一种适用于车身结构正向概念设计的新方法。采用传递矩阵法进行多体系统力学分析,无需建立系统总体动力学方程,涉及矩阵阶次低,计算速度快,适用于概念设计阶段车身结构方案频繁修改的需求,其基本流程如图3所示。
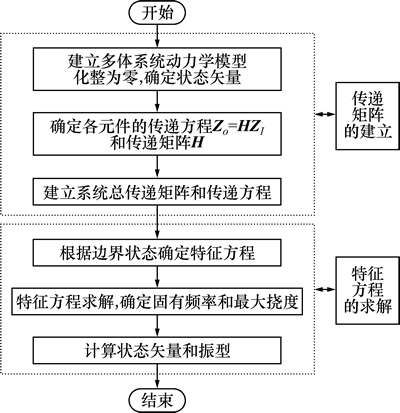
图3 多体系统建模求解流程
Fig. 3 Multi-body systems modeling and solving processes
2.1 车身动态刚度链建模
动态刚度链建模是为了分析和优化车身各主断面属性参数,避免车身产生共振,满足舒适性等要求。车身刚度链以主断面、接头等为节点,以载荷传递路径为链,描述结构与材料、载荷与变形,节点与节点之间的力学关系。车身整体刚度链由多个子刚度链耦合而成,可以按照车身结构特点分别建立每个子刚度链的计算模型,再向上逐层组合,最终建立车身的完整刚度链模型,如图4所示。
车身模态是评价车身动态特性的重要指标。与燃油车相比,纯电动汽车驱动装置为电动机,省去了发动机、变速箱甚至底盘结构中复杂的传动系统,因此,2种车身的动态特性有很大不同。首先需要分析电动车白车身自重状态下的自由模态。将传递矩阵法[9-10]的理论应用到车身结构分析中,推导车身动态刚度链数学模型,并用车身模态频率来衡量动态刚度[11],避免车身的一阶固有频率与载荷激振频率接近而产生共振。
依据图2所示简化几何模型和图4所示构成关系,车身的左侧围系统如图5所示(其中不带圈数字为节点编号,带圈数字为单元编号,圆形集中质量块标识),左侧围系统还可以再分解成若干个子系统。用同样的方法也可以处理右侧围系统和其他结构。

图4 车身整体刚度链的构成关系
Fig. 4 Composition relationship of body overall stiffness chain

图5 车身侧围力学模型及单元划分
Fig. 5 Side body mechanical model and unit division
在无外界载荷状态下建立左侧围动态刚度链模型。根据简化几何模型确定的拓扑关系、主断面分布、载荷位置等将车身侧围梁结构划分成12个单元和9个节点。其中单元编号以及对应的主断面编号和名称如表3所示。
表3 车身刚度链的分解
Table 3 Body stiffness chain decomposition

据主断面的作用,当表3中同一主断面对应多个组成单元时,这些组成单元可以具有相同的截面属性,则可将上述12个单元分类成9个主断面属性集合,记为{C}(i)={A I}(i)(其中,i为主断面编号,取值为1,2,…,9,且与表2中的编号一致;A为主断面面积即实心部分面积;I为主断面惯性矩)。
按照拓扑关系,车身侧围刚度链在耦合节点1和4处可拆分为2个子刚度链,分别为子刚度链1(0—1—2—3—4—5),子刚度链2(1—6—7—8—9—4),如图6所示。

图6 车身侧围动态刚度链分解
Fig. 6 Decomposition of side body dynamic stiffness chain
以子刚度链1为例建模(如图6(a)所示),节点0和节点5处为铰接约束,节点1和节点4处为耦合点,有各节点状态矢量以及耦合点未知状态矢量如下:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
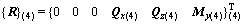 (5)
(5)
 (6)
(6)
式中:状态矢量Z包括3个位移分量即挠度y、横向位移x与转角θ,3个力分量为剪力Q、轴力N和弯矩M;{Z}l(i)和{Z}r(i)分别为单元i左、右端节点状态矢量;Ql和Qr分别为铰支处的径向约束反力;θl和θr分别为节点1和5处xoy平面内的转角;{R}(i)为节点i处的载荷矢量;Qx(i),Qz(i)和My(i)分别为节点i处轴向集中力、径向集中力和集中力偶。
分析梁的横向弯曲振动,将1个典型单元简化成包括1个无质量梁段和1个集中质量梁段。单元受力分析如图7所示,根据材料力学知识可得该单元场传递矩阵、点传递矩阵分别为:
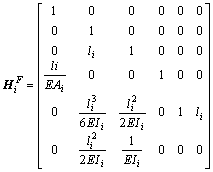 (7)
(7)
 (8)
(8)
式中:l(i)为单元i的长度;A(i)为单元i的截面(即主断面)面积;I(i)为单元i的截面惯性矩;ω为车身一阶固有频率。进而可得任一单元两端状态矢量之间的关系为
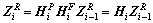
 (9)
(9)
此时,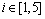 且
且 。根据传递矩阵推导公式可得出子刚度链1的传递方程为
。根据传递矩阵推导公式可得出子刚度链1的传递方程为

 (10)
(10)
其中:[H](i)为单元i的总传递矩阵。由车身结构特点可知,单元4的局部坐标系与全局坐标系有夹角,需进行坐标变换来求场矩阵。单元k的传递矩阵从局部坐标系变换到全局坐标系的变换公式为:
 (11)
(11)
 (12)
(12)
式中: 为单元k中无质量梁段在全局坐标系下的场矩阵;
为单元k中无质量梁段在全局坐标系下的场矩阵; 为单元k中质量块在全局坐标下的点矩阵;
为单元k中质量块在全局坐标下的点矩阵;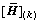 为局部坐标系下单元k的传递矩阵;
为局部坐标系下单元k的传递矩阵;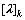 为单元k坐标转换矩阵。则单元4的场矩阵为
为单元k坐标转换矩阵。则单元4的场矩阵为
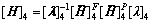 (13)
(13)
式中:
 (14)
(14)
α(4)为单元4的局部坐标系与全局坐标系的夹角。电动汽车车身动态特性可用车身模态频率评价,利用式(10)和(13)可建立各梁主断面属性{C}(i)与车身固有频率ω的关系。若以车身固有频率ω为基本未知向量并引入简支梁的边界条件,则子刚度链0—1—2—3—4—5—6—7的数学表达式可记为
 (15)
(15)
同理可得子刚度链2的数学模型。
子刚度链1与子刚度链2在节点1和节点4处耦合,在耦合节点处合力为零,位移矢量相等,建立两者的耦合方程:
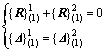 (16)
(16)
其中: 为子刚度链n耦合节点j上的载荷向量;
为子刚度链n耦合节点j上的载荷向量; 为子刚度链n上耦合节点j处的位移向量。将子刚度链1和2的数学表达式分别简记为f1和f2,耦合方程记为g(1,2)( f1,f2,{Q}(1,2)),得联立方程组:
为子刚度链n上耦合节点j处的位移向量。将子刚度链1和2的数学表达式分别简记为f1和f2,耦合方程记为g(1,2)( f1,f2,{Q}(1,2)),得联立方程组:
 (17)
(17)
式(17)为车身左侧围刚度链,简记为F1。同理可得出右车身侧围和7个横梁的刚度链,分别记为F2,F3,F4,…,F9。将这些子系统按照耦合点和拓扑关系组合,子系统刚度链i与子系统刚度链j的耦合方程记为G(i,j),则车身整体刚度链模型为
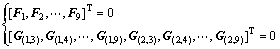 (18)
(18)
根据各子刚度链数学表达式及其耦合方程组可得车身固有频率ω与各主断面属性{C}(i)的函数关系式:
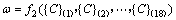 (19)
(19)

图7 单元受力分析
Fig. 7 Unit stress analysis
2.2 车身静态刚度链建模
弯曲刚度是评价电动车车身性能的1个重要指标。由于电动汽车载荷分布较传统车有较大差异,因此,根据静载荷分布优化分配各主断面属性参数至关重要。车身侧围力学模型及单元划分如图8所示,约束前悬架位置 X,Y和Z方向的平动自由度以及后悬架位置处Z方向的平动自由度,在座椅安装点左右对称施加垂直向下的力F=1 kN,则车身整体的弯曲刚度可由车身门槛梁处最大垂直挠度表示。
在利用传递矩阵法分析静态问题时,将梁结构简化为无质量的梁。与2.1中动态刚度链建模方法相同,同样以车身侧围为例,将车身侧围整体刚度链分解为子刚度链1和子刚度链2,如图9所示。

图8 车身侧围力学模型及单元划分
Fig. 8 Side body mechanical model and unit division

图9 车身侧围静态刚度链的拆解
Fig. 9 Decomposition of side body static stiffness chain
其中,单元划分以及建模过程与前述的动态刚度链相同,可得静态刚度链传递矩阵和传递方程如下:
 (20)
(20)
 (21)
(21)

 (22)
(22)
式(20),(21)和(22)分别为单元传递矩阵、单元i两端传递关系以及子刚度链1传递方程。此时,由于考虑车身承载,故在节点2处施加了外载荷矢量{R}(F)。综合考虑其他子刚度链,并按照耦合点及拓扑关系组合,可得整车静态刚度链模型为
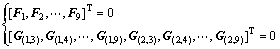 (23)
(23)
根据方程组(23)可以求得节点2竖直向下的变形量△z与各主断面{C}(i)的函数关系式:
 (24)
(24)
3 多目标优化及结果分析
3.1 车身主断面属性参数的多目标优化
车身主断面优化设计是一个多学科相互关联、相互耦合的过程[12]。下面综合考虑车身轻量化、弯曲刚度、模态等性能,采用多目标遗传算法[13]优化求解多个主断面的属性参数。
鉴于车身概念设计阶段主要任务是确定车身主断面力学性能,本文在综合分析常用薄壁梁弯扭刚度等特性的基础上,将电动车身主断面形状简化为由高度、宽度和厚度确定的矩形截面,如图10所示。

图10 矩形梁截面定义
Fig. 10 Define of rectangular cross-section beam
首先讨论刚度链1。选取的设计变量为侧围9个主断面的结构参数:
 (25)
(25)
其中:
 (26)
(26)
hi,wi和ti为第i个主断面简化截面结构参数。为了减少设计变量,根据统计分析,取主断面的长宽比为定值r,即r=w/h=1.35,则共有36个设计变量。考虑到概念设计阶段要求有较大的设计自由度,截面初始尺寸及变化范围设定如下:
门槛梁,h=w=150 mm,t=0.8 mm。
其余梁,h=w=80 mm,t=0.8 mm。
其中:h,w和t分别为梁截面的高度、宽度和厚度。
弯曲刚度要求当施加F=1 kN时,约束条件为加载点的位移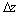 小于1 mm。现要求车身一阶固有频率不小于16.7 Hz,有:
小于1 mm。现要求车身一阶固有频率不小于16.7 Hz,有:
 (27)
(27)
 (28)
(28)
将车身质量作为目标函数,有
 (29)
(29)
其中:li为第i个梁结构的长度,可由车身简化几何模型得到;ρ为材料密度。由上述设计变量、目标函数和约束条件组成的优化模型为
 (30)
(30)
3.2 优化求解及结果分析
在MATLAB中调用遗传算法进行优化计算,优化的结果为:在满足弯曲刚度和固有频率约束条件下,车身最轻质量为0.163 t,加载点的位移为0.72 mm,一阶固有频率为18.62 Hz。迭代收敛过程和三目标优化结果见图11。车身质量与车身整体一阶固有频率的优化解见图12。

图11 三目标优化最优解集
Fig. 11 Solution set of three objective optimizations

图12 质量与一阶固有频率的2个目标优化解
Fig. 12 Two-objective optimization solution between vehicle weight and the first natural frequency
图11中,3个优化目标之间有一定的冲突性,1个目标的改善可能以降低其他目标的性能为代价,设计者可根据实际需要或凭借经验选择自己满意的最优解。从图12可以得出:在保证车身刚度基本不变的情况下,车身质量增加会导致车身整体模态下降。根据图11和图12所示优化结果可选出满足条件的最优解。优化后得到的主断面参数如表4所示。
表4 优化后的主断面参数
Table 4 Optimized main section parameters mm

车身弯曲刚度表达式为
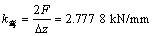 (31)
(31)
根据刚度链方法优化计算得出的主断面尺寸参数建立车身骨架有限元模型,并对其进行弯曲刚度和模态分析。在Nastran软件中采用四面体单元建立有限元模型,单元大小为10 mm,如图13所示,模型共由68 709个单元、65 239个节点组成。
弯曲工况下载荷和约束状态如图13所示。在门槛梁处施加载荷F以及分别对车身左、右前、左右后4个悬挂点的X,Y,Z自由度进行全约束。自由模态分析则不施加任何约束和力[14]。通过对车身骨架有限元模型进行静力以及模态分析,得出车身在2种工况下的整体变形分别如图14和图15所示。
由图14可以得出车身骨架最大变形约为0.76 mm,最大变形发生在门槛梁加载点附近,代入弯曲刚度计算式(31),得 2.631 6 kN/mm。
2.631 6 kN/mm。
由图15可以得出车身模态频率与车身变形间的关系,主要模态发生在车身顶部以及车身尾部,一阶模态频率为17.93 Hz。将有限元分析结果与刚度链计算结果对比,如表5所示。

图13 车身骨架的有限元模型
Fig. 13 Finite element model of body frame
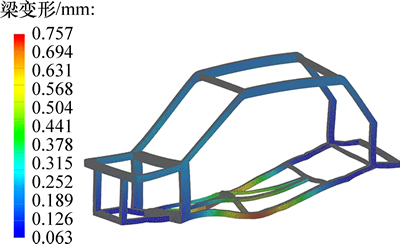
图14 车身骨架弯曲变形图
Fig. 14 Bending map of body frame
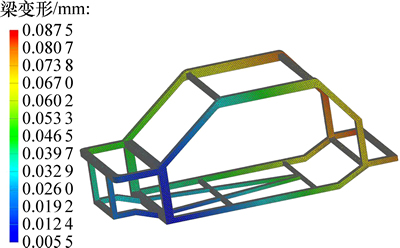
图15 车身骨架1阶模态振型
Fig. 15 First modal shape of body frame
表5 刚度链设计结果与有限元验证结果对比
Table 5 Comparison of results between stiffness chain design and finite element verify

从表5可知:用刚度链设计方法计算的概念车身弯曲刚度较有限元分析结果偏高,但误差在合理范围内,固有频率十分接近,且均避开共振频率,表明基于刚度链方法的主断面参数优化结果具有较高精度。
将本文方法用于某微型车车身骨架的分析优化,并将优化结果与文献[11]中同款车型的结果进行对比分析,如表6所示。可见这2种所得参数计算结果非常接近,进一步验证了本文方法的合理性和实用性。
表6 刚度链设计方法和某款微型车参数结果对比
Table 6 Comparison of results between stiffness chain design method and parameters in mini-car model

4 结论
1) 提出了用刚度链分析方法建立主断面属性参数与车身骨架弯曲刚度、模态等性能的关系,构建了包含主断面属性参数的白车身刚度链模型,可以用于优化车身结构的材料分布,实现刚度和模态性能最佳意义上的电动汽车车身轻量化设计。
2) 所提出的方法具有对车身结构性能的整体描述好、求解速度快、求解精度高的优点,是一种适用于电动汽车车身结构正向概念设计的新方法。
参考文献:
[1] CHAU K T, CHAN C C, CHAU K T. Modern electric vehicle technology[M]. Oxford: Oxford Science Publications, 2001: 5-9.
[2] MUSARDO C, RIZZONI G, GUEZENNEC Y, et al. A-ECMS: an adaptive algorithm for hybrid electric vehicle energy management[J]. European Journal of Control, 2005, 11(4): 509-524.
[3] 谢庆喜, 张维刚, 钟志华. 电动汽车电池架的耐撞性仿真设计与优化[J]. 汽车科技, 2005, 5(3): 25-28.
XIE Qingxi, ZHANG Weigang, ZHONG Zhihua. Crashworthiness optimization of battery box of a new designed electric vehicle[J]. Automotive Technology, 2005, 5(3): 25-28.
[4] 谢伦杰, 张维刚, 常伟波, 等.基于 SIMP 理论的电动汽车车身多目标拓扑优化[J]. 汽车工程, 2013, 35(7): 583-587.
XIE Lunjie, ZHANG Weigang, CHANG Weibo. Multi-objective topology optimization for electric car body based on the SIMP theory[J]. Automotive Engineering, 2013, 35(7): 583-587.
[5] 张伟, 侯文彬, 胡平. 基于拓扑优化的电动汽车白车身优化设计[J]. 湖南大学学报(自然科学版), 2014, 41(10): 42-48.
ZHANG Wei, HOU Wenbin, HU Ping. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University(Natural Science), 2014, 41(10): 42-48.
[6] NORBEG E, L VGREN S. Topology optimization of vehicle body structure for improved ride & handling[D]. Link
VGREN S. Topology optimization of vehicle body structure for improved ride & handling[D]. Link ping: Link
ping: Link ping University. Mechanical Engineering Department, 2011: 13-28.
ping University. Mechanical Engineering Department, 2011: 13-28.
[7] QUINN G C. Full automobile topology design optimized to maximize structural stiffness subject to multiple static load cases including inertial relief[C]//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. Fort Worth, America, 2010: 13-15.
[8] 田海豹. 基于刚度链方法的车身概念设计研究[D]. 长沙: 湖南大学机械与运载工程学院, 2013: 47-56.
TIAN Haibao. Study on conceptual design of car body using stiffness chain[D]. Changsha: Hunan University. Mechanical and Automotive Engineering, 2013: 47-56.
[9] 刘庆潭, 倪国荣. 结构分析中的传递矩阵法[M]. 北京: 中国铁道出版社, 1997: 1-19.
LIU Qingtan, Ni Guorong. Structural analysis of the transfer matrix method in Beijing[M]. Beijing: China Railway Press, 1997: 1-19.
[10] QINGNING L. The transfer matrix method of bar elements with variable cross-section[J]. Journal of Xi’an University of Architecture & Technology, 2001, 5(1): 18-23.
[11] 张越. 某微型电动轿车车身骨架有限元及试验分析[D]. 武汉: 武汉理工大学汽车工程学院, 2008: 41-42.
ZHANG Yue. Finite element and test analysis on the body frame structure of a Mini–EV[D]. Wuhan: Wuhan University of Technology. School of Automotive Engineering, 2008: 41-42.
[12] KODIYALAM S, YANG R J, GU L, et al. Multidisciplinary design optimization of a vehicle system in a scalable, high performance computing environment[J]. Struct Multidisc Optim, 2004, 2(4): 256-263.
[13] 王平, 郑松林, 吴光强. 基于协同优化和多目标遗传算法的车身结构多学科优化设计[J]. 机械工程学报, 2011, 47(2): 102-108.
WANG Ping, ZHENG Songlin, WU Guangqiang. Multidisciplinary design optimization of vehicle body structure based on collaborative optimization and multi-objective genetic algorithm[J]. Journal of Mechanical Engineering, 2011, 47(2): 102-108.
[14] 王友成. 某款电动汽车框架车身结构分析及优化[D]. 合肥: 合肥工业大学机械制造及其自动化学院, 2012: 33-42.
WANG Youcheng. Structural analysis and optimization of a electric car frame body[D]. Hefei: Hefei University of Technology. School of Mechanical and Automotive Engineering, 2012: 33-42.
(编辑 陈灿华)
收稿日期:2016-05-12;修回日期:2016-07-23
基金项目(Foundation item):国家自然科学基金资助项目(51475152)(Project(51475152) supported by the National Natural Science Foundation of China)
通信作者:刘子建,博士,教授,博士研究生导师,从事车身刚度链理论、机械精度链理论、产品信息模型理论研究;E-mail:zijianliu@hnu.edu.cn