文章编号:1004-0609(2015)-09-2350-08
镁合金正挤压-扭转变形的数值模拟与实验研究
卢立伟1, 2,赵 俊1,陈胜泉1,刘龙飞1,曾文兵1
(1. 湖南科技大学 高温耐磨材料及制备技术湖南省国防科技重点实验室, 湘潭 411201;
2. 中南大学 材料科学与工程学院,长沙 410083)
摘 要:结合传统挤压与扭转变形的特点提出正挤压-扭转复合变形方式,采用有限元软件对其变形方式进行数值模拟。研究扭转角度对坯料变形过程中累积应变的影响,并对经过不同扭转角度变形后坯料的等效应变分布的不均匀程度进行定量分析。根据正挤压-扭转复合变形的模拟结果,设计出较优的模具结构并进行实验研究。结果表明:正挤压-扭转复合变形可以显著提高镁合金变形过程的累积应变,随着扭转角度的增大,累积应变增大,但不均匀程度相对增加,最大等效应变高达3.75。当模具扭转角为40°时,试样可获得较大的等效应变和均匀的等效应变分布。在复合变形后,AZ31镁合金的晶粒尺寸由300 μm显著细化至约6 μm。
关键词:AZ31镁合金;有限元模拟;复合挤压变形;等效应变分布
中图分类号:TG376 文献标志码:A
Numerical simulation and experimental research of AZ31 Mg alloys processed by direct extrusion and torsional deformation
LU Li-wei1, 2, ZHAO Jun1, CHEN Sheng-quan1, LIU Long-fei1, ZENG Wen-bing1
(1. Hunan Provincial Key Defense Laboratory of High Temperature Wear-resisting Materials and
Preparation Technology, Hunan University of Science and Technology, Xiangtan 411201, China;
2. School of Materials Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Combining the feature of traditional extrusion and torsional deformation, direct extrusion and torsional compound deformation was proposed, and numerical simulation of deformation process was investigated using finite element software. Effect of torsion angle on cumulative strain during the deformation process was studied, and the non-uniformity of the equivalent strain distribution after different torsion angle deformation was also analyzed quantitatively. According to the simulation results of direct extrusion and torsional deformation, reasonable die structure was designed, and experimental research was carried out. The results show that the direct extrusion and torsional compound deformation can significantly enhance the accumulation strain of deformed magnesium alloys, and the cumulative strain increases with the increase of torsional angle, the maximum equivalent strain can get up to 3.75, but the degree of nonuniformity increases relatively. The specimen can obtain larger and more uniform distribution of equivalent strain for torsion angle of 40°. After compound deformation, the grain size of AZ31 magnesium alloy can be significantly refined from 300 μm to about 6 μm.
Key words: AZ31 magnesium alloy; finite element simulation; compound extrusion; equivalent strain distribution
镁及镁合金作为最轻的结构材料,越来越被大规模地推广应用,近年来对于研究变形镁合金的塑性成型技术已成为世界镁工业发展的重要研究领域,对于如何更有效地提高镁合金的塑性成形能力成为研究热点[1-2]。传统挤压工艺生产的镁合金无法得到强度与 塑性较好的变形镁合金,主要表现在晶粒尺寸粗大、组织不均匀分布,力学性能的各向异性[3]。等径角挤压(ECAE)作为一种常见的大塑性变形方法最早由SEGAL[4]提出,可通过多道次的挤压从而得到高性能的镁合金,但由于多道次挤压工艺的不连续,耗费成本高且很难大规模的应用,促使学者不断地研究新型的大塑性变形方式来获得超细晶的金属结构材料[5-6]。FATEMI-VARZANEH等[7]运用累积抵抗挤压技术(ABE)成功地实现了AZ31镁合金低温挤压,取得了 较好的晶粒细化效果。刘天模等[8]将等径角挤压方法的出口通道截面减小,提出一种将等径角挤压和大比例挤压相结合的变通道角挤压(CCAE),并结合实验证明了该方法可一道次挤压成型制备出晶粒细小均匀且力学性能良好的变形镁合金。薛克敏等[9]为改进ECAE的不足,提出了等径角挤扭新工艺(ECAE-T),着重分析了纯铝在该工艺挤压过程中应力应变大小和分布,并自行设计模具进行实验验证。结果表明,模拟与实验结果基本一致,ECAE-T能累积更大的剪切变形量和得到更细化的组织。胡红军[10]依据正挤压与多道次等通道挤压的特点提出了挤压-剪切复合的挤压工艺(ES),对AZ31镁合金进行了模拟和实验研究。结果表明,ES挤压工艺对细化镁合金的显微组织效果显著。对于研究镁合金挤压及生产实践中的模具设计优化需要大量的实验研究结果及验证,其实验周期长、耗费成本高,对不同工艺模具的参数进行实验,实验周期更长,设备的损耗也更大[3]。越来越多的研究结果表明[11],有限元模拟可成功辅助制定实验方案、分析实验结果,达到减小实验工作量、降低实验成本和提高实验精度等目标。
因此,本文作者提出镁合金的正挤压-扭转复合变形新方式,对AZ31镁合金进行正挤压-扭转变形的有限元分析和实验研究。正挤压-扭转复合变形是将
扭转剪切结构赋予传统正挤压成型通道处,使得金属正挤压变形后再次发生扭转剪切变形,扭转剪切变形可改变金属的流动方向,使金属产生旋转性流动。此外,正挤压产品再次经历扭转剪切变形时,金属需要承受的更大的压力来实现材料的挤出成型,增加的压力可改善镁合金的塑性成型能力[10]。
1 模拟参数和实验方法
正挤压-扭转变形复合挤压是由正挤压的挤压比变形区和扭转变形区两部分组成,如图1所示。模具由一个凸模和两个带有挤压比区和扭转区通道的凹模所组成。扭转结构主要涉及两个重要的工艺参数,即模具剪切角γ和试样横截面扭转角φ。剪切角γ是指两椭圆截面相同点连线与模具通道轴线方向的夹角,扭转角φ是指扭转变形前后试样横截面的旋转角度。一般来说,剪切角和扭转角越大,表明材料所承受的变形越剧烈,试样累积应变量也就越大。通过改变扭转区的上下椭圆截面的对应位置可控制扭转角度的大小,当扭转角度为φ时,取椭圆上任意一点(x=acosθ , y=bsinθ),由图2计算可得出模具剪切角与扭转角存在如下关系:
x2=2[(acosθ)2+(bsinθ)2]-2cosφ[(acosθ)2+(bsinθ)2] (1)
 (2)
(2)
 (3)
(3)
式中:L为扭转区长度;a为椭圆截面长轴长度;b为椭圆截面短轴长度;θ为椭圆参数。
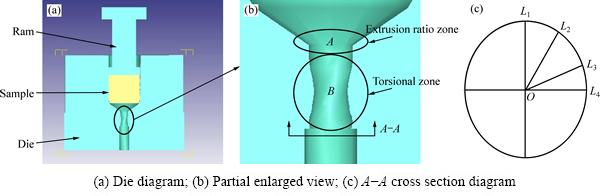
图1 复合挤压建模示意图
Fig. 1 Schematic models of compound extrusion
挤压时,将试样放入通道中,试样经过挤压比变形区的挤压比变形和扭转变形区域的旋转剪切变形,受到挤压、扭转应力和挤压热的作用,金属可连续发生动态再结晶从而细化晶粒。研究结果表明,动态再结晶需要累积应变超过极限应变时方可发生[12],其公式如式(4)和(5)所示:
 (4)
(4)
 (5)
(5)
式中: 为动态再结晶发生时的应变;
为动态再结晶发生时的应变; 为最大流动应力对应的应变;a1和a2均为系数;
为最大流动应力对应的应变;a1和a2均为系数;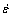 为应变速率;n1、m1和C1均是与材料有关的常数;Q为激活能,kJ/mol;R为摩尔气体常数(8.31 J/mol);T为变形温度;d0为初始晶粒尺寸。
为应变速率;n1、m1和C1均是与材料有关的常数;Q为激活能,kJ/mol;R为摩尔气体常数(8.31 J/mol);T为变形温度;d0为初始晶粒尺寸。
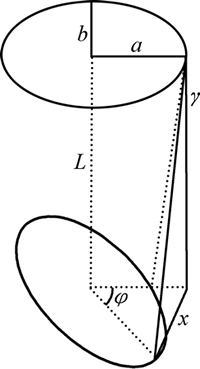
图2 扭转原理图
Fig. 2 Principle diagram of twist
针对正挤压-扭转复合变形挤压过程在Deform-3D软件中进行模拟研究。在模拟过程中,料筒直径为30 mm,挤压比区的直径为10 mm,长度为5 mm,扭转区截面为长轴a=10 mm,短轴b=8 mm的椭圆,长度8 mm,正挤压区与扭转区之间采用圆滑过渡,扭转角度分别取为20°、30°、40°和50°。为了方便对比扭转角度对镁合金变形的结果,本次实验中选取挤压比均为9,挤压温度为300℃,挤压速度为1mm/s。已有研究表明[13],当挤压速度较低时,试样与模具间的摩擦所引起的挤压温度变化可忽略不计。挤压试样直径为30 mm,长度为60 mm。对试样划分相对网格数目为20000,实验模型为: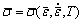 ,输入材料的应力-应变曲线指定材料的屈服服从Von Mises屈服准则,试样和模具间的接触容差为0.046 mm,体积补偿为43786.9 mm3。选用剪切摩擦类型,摩擦因数为0.4。本实验中,采用Direct Iteration迭代法和Conjugate-Gradient求解器。采用的速度收敛误差限为0.005,失衡力收敛误差限为0.05。在实际加工过程中,不考虑凸模和凹模的变形情况,将凸模和凹模定义为刚性体,挤压试样定义为塑性体,其运动关系定义为凹模静止不动,凸模为主动件,挤压试样视为从动件。为了后续研究经不同扭转角度变形后试样横截面的应变分布规律,取如图1(c)所示A-A截面沿L1~L4 4条直线应变分析。为验证有限元分析结果,选用模具参数正挤压挤压比为9、扭转角度为40°进行正挤压-扭转变形复合模型加工实验,自制模具如图3所示。经正挤压-扭转变形后,取棒料的中心部位进行显微组织观察,采用乙酸苦味酸溶液进行金相腐蚀,并在光学显微镜上分别沿平行挤压方向(ED)和垂直于ED方向进行显微组织观察。
,输入材料的应力-应变曲线指定材料的屈服服从Von Mises屈服准则,试样和模具间的接触容差为0.046 mm,体积补偿为43786.9 mm3。选用剪切摩擦类型,摩擦因数为0.4。本实验中,采用Direct Iteration迭代法和Conjugate-Gradient求解器。采用的速度收敛误差限为0.005,失衡力收敛误差限为0.05。在实际加工过程中,不考虑凸模和凹模的变形情况,将凸模和凹模定义为刚性体,挤压试样定义为塑性体,其运动关系定义为凹模静止不动,凸模为主动件,挤压试样视为从动件。为了后续研究经不同扭转角度变形后试样横截面的应变分布规律,取如图1(c)所示A-A截面沿L1~L4 4条直线应变分析。为验证有限元分析结果,选用模具参数正挤压挤压比为9、扭转角度为40°进行正挤压-扭转变形复合模型加工实验,自制模具如图3所示。经正挤压-扭转变形后,取棒料的中心部位进行显微组织观察,采用乙酸苦味酸溶液进行金相腐蚀,并在光学显微镜上分别沿平行挤压方向(ED)和垂直于ED方向进行显微组织观察。

图3 正挤压-扭转复合变形模具结构及挤压试样照片
Fig. 3 Die of direct extrusion and torsional composite method (a) and extrusion samples (b)
2 结果与分析
2.1 扭转角度对等效应变分布的影响
图4所示为扭转角度分别为20°、30°、40°、50°模具下AZ31镁合金试样纵截面上的等效应变分布。通过分析其应变分布可以得到试样在挤压过程中变形程度。从图4可以看出,正挤压-扭转变形试样主要分为3个区域:Ⅰ区为料头区,该部分区域在挤压过程首先发生变形,变形自由度大,情况复杂,因此在变形过程中应变分布极不均匀,在实际应用变形过程中,该部分的材料通常作为废料将其去除;Ⅱ区为扭转变形区,等效应变在试样边缘到中心具有明显的梯度变化,等效应变集中在2.25~3.75。对于不同扭转角度的模具,由图4(a)和(e)可以看出,当扭转角度为20°时,试样边缘基本无等效应变的增加,应变均匀性良好,经过正挤压变形后等效应变无明显的增大,等效应变为3.0,表明扭转角度小无法进一步增大变形量。随着扭转角度的增大,由图4(b)~(d)和(f)~(h)可知,试样的边缘等效应变增大,等效应变在横向上的变形不均匀性也开始增大,但整体等效应变的数值增大,表明试样在经过扭转挤压区时,由于模具内壁的改变使得金属的流动方向发生变化,使得金属边缘部位最先产生剪切变形,由于金属流动具有连续性,边缘处金属牵扯内部金属扭转变形。在旋转和剪切的双重作用下,挤压效率随着扭转角度的增大而增大,最大等效应变由3.38增大至3.75,扭转角为50°时比扭转角为20°的等效应变提高了25%。相比于GHAZANI等[14]所报道的一周期循环交叉等通道挤压后的等效应变值3.4还要高。因此可得出大的扭转角能够使材料的变形程度增加,累积更大的塑性应变量,可为进一步细化晶粒提供条件,为扭转工艺的合理性提供一定的理论依据;Ⅲ区为挤压比变形区。由图4可看出,试样在变形区等效应变呈梯度分布,为主要变形区,等效应变的大小主要由挤压比所决定。随着变形的继续,试样进入扭转变形区,其等效应变增加,但应变均匀性变差。

图4 不同扭转角模具试样等效应变分布等值线图和云图
Fig. 4 Line contour ((a)-(d)) and solid ((e)-(h)) of equivalent strain distribution for die with different twist angles
2.2 等效应变均匀性分析
为了定量分析扭转角对等效应变均匀性分布的影响,取经过正挤压和扭转变形后的挤压试样的A-A横截面进行观察,由于圆形的正挤压-扭转复合变形为三维变形,变形存在对称关系,因此对图1(c)中L1~L4线等效应变分布曲线对比分析。图5所示为经过不同扭转角度变形后试样L1~L4分布的等效应变曲线。由图5(a)可知,扭转角为20°时,4条线对应的等效应变分布基本重合,这表明扭转角为20°时试样的等效应变在横截面上的变化不大,等效应变分布均匀,但等效应变值较小。随着扭转角的增大,直线L1~L2增长趋势增大。当扭转角为50°时,呈最明显增长趋势,表明当扭转角为50°时,试样边缘应变变化剧烈,等效应变不均匀性增加,试样的边缘部分为主要的变形部分。

图5 不同模具试样成型后A-A截面等效应变分布
Fig. 5 Equivalent strain distributions in A-A section for die with different twist angles
为了更清楚的分析试样横截面的等效应变分布均匀程度,对代表等效应变不均匀程度的参数Ci进行计算[15]:
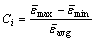 (6)
(6)
式中: 、
、 、
、 分别为横截面上等效应变的最大值、最小值和平均值,等效应变的平均值由式(7)求得:
分别为横截面上等效应变的最大值、最小值和平均值,等效应变的平均值由式(7)求得:
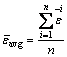 (7)
(7)
根据式(6)和(7)可将经过不同扭转角度后A-A截面的等效应变不均匀程度参数Ci结果计算如表1所列。由表1可知,当扭转角度为20°时,A-A截面的最小等效应变和最大等效应变为2.98和3.18,而当扭转角度为50°时,最小等效应变和最大等效应变增大至3.40和3.75。对于等效应变不均匀程度而言,当扭转角度为20°时,Ci的值为0.066,虽然变形比较均匀,但获得的等效应变相对比较小,不足以更大程度地达到细化晶粒的效果。比较不同模具结构的变形情况发现,随着扭转角度的增加,A-A截面的最大和最小等效应变增大,不均匀程度参数Ci集中在0.066~0.101。任国成等[16]对不同ECAP模具外角的等效应变分布进行模拟,外角为37°和90°时,平均等效应变分别为1.048、0.883,不均匀程度参数Ci分别为0.451、0.583。当外角为20°时,平均等效应变为1.228,不均匀程度参数Ci为0.194,相对于外角为37°和90°模具获得了比较好的等效应变分布,但整体来说一道次等效应变不大,晶粒细化效果不好。任国成等[17]将试样沿A、Ba、Bc、C不同路径4道次ECAP挤压后,平均等效应变分别为5.15、4.86、4.98、5.02,就不均匀程度Ci而言,分别为0.384、0.212、0.069、0.107,4种变形路径都取得了较大的等效应变,不均匀程度也比较好,但进行了4道次的变形。根据以往和本次模拟结果分析可知,当正挤压-扭转复合变形模具的扭转角为40°时,可获得较高的平均等效应变和良好均匀性分布。
表1 A-A截面等效应变不均匀程度参数
Table 1 Non-uniformity parameters of equivalent strain across section A-A

2.3 显微组织观察
图6所示为铸态AZ31镁合金原试样及正挤压-扭转复合变形后试样纵截面和横截面的光学显微组织。由图6(a)可见,铸态AZ31镁合金经均匀化处理后组织比较均匀,晶粒晶界呈明显的等轴分布,平均晶粒尺寸约为300 μm,析出相基本消除,为挤压实验做好了良好的组织准备。由图6(b)、(c)可知,经过正挤压-扭转复合变形工艺一道次挤压后无论是纵截面还是横截面均发现晶粒明显细化,但试样组织整体分布不均匀,试样局部区域仍然存在较粗大的晶粒。横截面中呈现出“双峰组织”,粗大晶尺寸约为15~20 μm,细小晶粒尺寸为3~4 μm,平均晶粒尺寸约为6 μm。观察发现,细小的晶粒分布方向不明显。经观察纵截面的显微组织发现,AZ31镁合金铸锭中原始大晶粒在挤压力和扭转的作用下发生转动,材料的显微组织发生了显著变化,出现大量与挤压轴线呈一定角度方向排布的细小晶粒和少量未发生再结晶的长条状晶粒[18],细小晶粒呈典型的剪切带状,内部晶粒大小不均匀,小晶粒的尺寸约5 μm,然而大的晶粒尺寸竟达到30 μm,长条状晶粒、剪切带和大小不均晶粒的存在说明挤压过程中动态再结晶发生不充分,这主要是由温度和挤压速度所决定,试样内部的部分组织来不及发生充分的动态再结晶,从而造成内部组织不均匀,且这种现象将会对试样的力学性能产生不利的影响[19]。已有研究表明,尽管传统的正挤压也能获得小于10 μm 的镁合金晶粒组织,但是挤压比为35,远大于正挤压-扭转复合变形后的挤压比9[20];此外,在ECAE研究中发现[21],经过1、5、8道次挤压可以在挤压温度523 K时,使AZ31镁合金从初始的25 μm细化至5、3.8和2.9 μm。总体上来讲,正挤压-扭转复合变形技术在细化镁合金晶粒尺寸方面显示出了独特的优越性。

图6 AZ31镁合金原试样及一道次变形后纵截面和横截面的光学显微组织
Fig. 6 Optical microstructures of AZ31 magnesium alloys unprocessed and processed by one pass
3 结论
1) AZ31镁合金经历墩粗到扭转变形,等效应变呈梯度增加,在正挤压挤压比区和扭转变形区域尤为突出,合适的扭转角度能有效地提高变形累积的应变量,可充分诱发晶粒破碎和动态再结晶。
2) 在正挤压-扭转复合变形挤压过程中,当扭转角度较小时,试样的平均等效应变小,变形不均匀程度小,随扭转角度的增大,试样的平均等效应变增大,但变形不均匀程度增大。
3) 扭转角为40°的正挤压-扭转复合模具,可获得较高且均匀的等效应变分布,平均等效应变为3.38,不均匀程度参数Ci为0.068。AZ31 镁合金经实际正挤压-扭转变形后,晶粒尺寸得到显著细化。
REFERENCES
[1] 王天一, 丁汉林, 刘育锋, 魏 峰, 张义伟, 程广萍. Mg-1.0%Zn-1.5%Ca合金热压缩过程的显微组织及动态再结晶行为[J]. 中国有色金属学报, 2014, 24(10): 2474-2481.
WANG Tian-yi, DING Han-lin, LIU Yu-feng, WEI Feng, ZHANG Yi-wei, CHENG Guang-ping. Microstructure and dynamic recrystallization behavior of Mg-1.0%Zn-1.5%Ca alloy during hot compression[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2474-2481.
[2] 张晓华, 姜巨福, 罗守靖. AZ91D镁合金的热压缩变形行为[J]. 中国有色金属学报, 2009, 19(10): 1720-1725.
ZHANG Xiao-hua, JIANG Ju-fu, LUO Shou-jing. Compression deformation behavior of AZ91D magnesium alloy at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(10): 1720-1725.
[3] 胡红军. 镁合金挤压-剪切变形行为的物理和数值模拟研究[J]. 稀有金属材料与工程, 2013, 42(5): 957-961.
HU Hong-jun. Physical and numerical simulation of deformation behaviors of extrusion-shear for magnesium alloy[J]. Rare Metal Materials and Engineering, 2013, 42(5): 957-961.
[4] SEGAL V M. Materials processing by simple shear[J]. Materials Science and Engineering A, 1995, 197: 157-164.
[5] 孔 晶, 侯文婷, 彭勇辉, 康志新, 李元元. T 型通道挤压变形 ZK60 镁合金的组织与力学性能[J]. 中国有色金属学报, 2011, 21(6): 1199-1204.
KONG Jing, HOU Wen-ting, PENG Yong-hui, KANG Zhi-xin, LI Yuan-yuan. Microstructure and mechanical properties of ZK60 magnesium alloy processed by T-shape channel pressing[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(6): 1199-1204.
[6] 刘天模, 刘建忠, 卢立伟, 袁晗琦, 时秀玲, 潘复生. 双向双通道变通径挤压 AZ31 镁合金的显微组织及变形行为[J]. 中国有色金属学报, 2010, 20(9): 1657-1664.
LIU Tian-mo, LIU Jian-zhong, LU Li-wei, YUAN Han-qi, SHI Xiu-ling, PAN Fu-sheng. Microstructure and deformation behavior of dual-directional extruded AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(9): 1657-1664.
[7] Fatemi-Varzaneh S M, Zarei-Hanzaki A. Processing of AZ31 magnesium alloy by a new noble severe plastic deformation method[J]. Materials Science and Engineering A, 2011, 528(3): 1334-1339.
[8] 刘天模, 刘世宇, 彭天成, 刘建忠, 刘 宇, 潘复生. AZ31镁合金变通道角挤压工艺[J]. 材料热处理学报, 2009, 30(5): 64-67.
LIU Tian-mo, LIU Shi-yu, PENG Tian-cheng, LIU Jian-zhong, LIU Yu, PAN Fu-sheng. Change channel angular extrusion process of AZ31 magnesium alloy[J]. Transactions of Materials and Heat Treatment, 2009, 30(5): 64-67.
[9] 薛克敏, 吴战立, 李 萍, 王晓溪, 贾建磊. 纯铝等径角挤扭新工艺数值模拟及实验研究[J]. 中国机械工程, 2010, 21(12): 1485-1489.
XUE Ke-min, WU Zhan-li, LI Ping, WANG Xiao-xi, JIA Jian-lei. Simulation and experimental research on a new technique named equal channel angular extrusion and twist prepared by pure aluminum[J]. China Mechanical Engineering, 2010, 21(12): 1485-1489.
[10] 胡红军. 挤压剪切与正挤压对AZ31镁合金塑性变形的影响[J]. 材料热处理学报, 2014, 35(4): 202-207.
HU Hong-jun. Effects of extrusion-shear and direct extrusion on the plastic deformation of AZ31 magnesium alloy[J]. Transactions of Materials and Heat Treatment, 2014, 35(4): 202-207.
[11] 于彦东, 周 浩. MB15合金等通道转角挤压组织模拟和实验分析[J]. 中国有色金属学报, 2011, 21(2): 296-302.
YU Yan-dong, ZHOU Hao. Simulation and experiment analysis of grain structure of MB15 alloy prepared by equal-channel angular pressing[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(2): 296-302.
[12] 卢立伟, 刘天模, 陈 勇, 吕城龄. AZ31镁合金挤压长条晶粒的形成机理与消除方法[J]. 材料热处理学报, 2011, 32(12): 17-22.
LU Li-wei, LIU Tian-mo, CHEN Yong,  Cheng-ling. Formation and elimination of elongated grains in extruded AZ31 magnesium alloy[J]. Transactions of Materials and Heat Treatment, 2011, 32(12): 17-22.
Cheng-ling. Formation and elimination of elongated grains in extruded AZ31 magnesium alloy[J]. Transactions of Materials and Heat Treatment, 2011, 32(12): 17-22.
[13] 乔 端, 钱仁根. 非线性有限元及其在塑形加工中的应用[M]. 北京: 冶金工业出版社, 1990.
QIAO Ri, QIAN Ren-gen. Nonlinear finite element method and its application in the plastic processing[M]. Beijing: Metallurgical Industry Press, 1990.
[14] GHAZANI M S, EGHBALI B. Finite element simulation of cross equal channel angular pressing[J]. Computational Materials Science, 2013, 74: 124-128.
[15] LI S, BOURKE M A M, BEYERLEIN I J, ALEXANDER D J, CLAUSEN B. Finite element analysis of the plastic deformation zone and working load in equal channel angular extrusion[J]. Materials Science and Engineering A, 2004, 382(1/2): 217-236.
[16] 任国成, 赵国群, 徐淑波, 王桂青. AZ31镁合金等通道转角挤压变形均匀性有限元分析[J]. 中国有色金属学报, 2011, 21(4): 848-855.
REN Guo-cheng, ZHAO Guo-qun, XU Shu-bo, WANG Gui-qing. Finite element analysis of homogeneous deformation of AZ31 magnesium during equal channel angular pressing process[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(4): 848-855.
[17] 任国成, 赵国群. AZ31镁合金等通道转角挤压应变累积均匀性分析及组织性能研究[J]. 材料工程, 2013(10): 13-19.
REN Guo-cheng, ZHAO Guo-qun. Homogeneous deformation analysis and microstructure properties study of AZ31 magnesium alloy in multi-pass equal channel angular pressing[J]. Journal of Materials Engineering, 2013(10): 13-19.
[18] HU H J, Zhang D F, Pan F S. Analysis of the cracks formation on surface of extruded magnesium rod based on numerical modeling and experimental verification[J]. Acta Metallurgica Sinica, 2009, 22(5): 353-364.
[19] LU L W, LIU T M, CHEN Y, WANG Z C. Deformation and fracture behavior of hot extruded Mg alloys AZ31[J]. Materials Characterization, 2012, 67: 93-100.
[20] 张宝红, 张治民, 李大旭. 正挤压对铸态AZ31镁合金组织与性能的影响[J]. 轻合金加工技术, 2009, 37(10): 39-41.
ZHANG Bao-hong, ZHANG Zhi-min, LI Da-xu. Influence of direct extrusion on microstructure and mechanical properties of as-cast AZ31 magnesium alloy[J]. Light Alloy Fabrication Technology, 2009, 37(10): 39-41.
[21] 胥广亮, 陈国清, 周文龙, 付雪松, 任 晓, 孙中刚. 等径角挤压对AZ31镁合金组织及力学性能的影响[J]. 材料工程, 2011(2): 69-72
XU Guang-liang, CHEN Guo-qing, ZHOU Wen-long, FU Xue-song, REN Xiao, SUN Zhong-gang. Effect of equal channel angular extrusion on the microstructure and mechanical properties of AZ31 magnesium alloy[J]. Journal of Materials Engineering, 2011(2): 69-72.
(编辑 王 超)
基金项目:湖南省自然科学基金资助项目(14JJ3111);湖南省教育厅项目(14C0455);湖南省自然科学湘潭联合基金资助项目(13JJ8017);湖南省大学生研究性学习和创新性试验计划项目(201410534005)
收稿日期:2014-12-15;修订日期:2015-07-06
通信作者:卢立伟,讲师,博士;电话:0731-58290047;E-mail:cqulqyz@126.com