DOI: 10.11817/j.issn.1672-7207.2015.09.047

基于结构-声耦合法研究高铁铝型材的隔声性能

罗乐¹，郑旭¹，郝志勇¹，吕义²

(1. 浙江大学 能源工程学系，浙江 杭州，310027；

2. 长春轨道客车股份有限公司，吉林 长春，130000)

摘要：采用脉冲衰减法测量得到铝型材的内损耗因子作为仿真的结构阻尼参数，应用结构-声耦合法计算铝型材样件在100~1 600 Hz中心频段内的隔声量(STL)，并通过与试验对比，验证仿真方法的可靠性。选取3种不同几何断面的铝型材并对比其隔声性能。研究结果表明：侧墙铝型材的隔声性能相对最优，面密度最大的地板铝型材次之，顶板铝型材在500~1 250 Hz内有较宽的隔声谷，隔声性能最差。

关键词：高速列车；铝型材；结构-声耦合；隔声量；内损耗因子

中图分类号：TB532             文献标志码：A         文章编号：1672-7207(2015)09-3513-07

Sound insulation performance analysis of high-speed train aluminum extrusions based on structure-sound coupling method

LUO Le¹, ZHENG Xu¹, HAO Zhiyong¹, L Yi²

(1. Department of Energy Engineering, Zhejiang University, Hangzhou 310027, China;

2. Changchun Railway Vehicles Co. Ltd., Changchun 130000, China)

Abstract: Impulse response decay method was proposed to estimate internal loss factor of the aluminum extrusion, which was defined as the structure damping parameter in simulation. Then the sound transmission loss (STL) curves of aluminum extrusion sample between 100 and 1 600 Hz were calculated by structure-sound coupling method, which was validated in comparison with experiment results. STL of aluminum extrusions with three different cross-sections were computed and analyzed contrastively. The results indicate that the sound insulation of side extruded panel is the best, followed by the floor panel with the largest surface density. The roof panel, whose STL curve has a broad band valley between 500 and 1 250 Hz, possesses the worst sound insulation performance.

Key words: high speed train; aluminum extrusions; structure-sound coupling; sound transmission loss; internal loss factor

我国的高速铁路网正日趋完善，乘坐高速列车可极大地提升人们的出行效率和安全保障。然而随着车速的不断提升，高速列车的振动噪声问题日益突出，是亟待解决的课题之一^[1-3]。铝型材是目前高速列车白车身的主体板件，当车体受到外部噪声源的激励时，铝型材是固体声的主要传播途径，其隔声性能的优劣直接决定噪声能量的衰减程度，进而影响乘客体验的舒适度。因此，研究铝型材的隔声特性，对高速列车的车内噪声预测和整车减振降噪等方面都具有重要的工程指导意义。铝型材是典型的双层板结构，国内外学者对此类板件的隔声问题已有一定的研究基础。Wang等^[4]基于空间谐波展开法推导了平行加筋的无限大双层板的隔声公式；Xin等^[5]建立了正交加筋双层板的声透射计算模型，并讨论板间距、填充介质和刚度质量比等因素的影响。但目前理论模型的通用性较差，还无法应用在大型复杂的工程结构件上。Kim等^[6-7]分别对不同型号高速列车的主体板件，即蜂窝复合铝板和中空挤压铝型材进行大量的隔声试验和声学包装研究，但并未结合仿真进一步总结其隔声性能的一般变化规律。在数值计算方面，Kim等^[8]基于结构有限元法预测铝型材在中低频段的隔声性能，但由于结构的阻尼参数未知，仿真与试验结果尚存在一定差距；Xie等^[9]考虑结构与声腔的耦合作用，并结合统计能量分析方法计算铝型材高频段的隔声量，但目前对于子系统的定义和划分普遍存在主观性，尚缺少权威的判断准则。基于这一背景，本文作者拟系统研究高铁铝型材的隔声性能，研究对象是应用在CRH3动车组上的中空挤压铝型材，几何断面较为复杂多样。首先，以铝型材实体样件为例，基于脉冲衰减法测试得其阻尼参数，并采用结构-声耦合法对100~1 600 Hz频段内的隔声量进行数值计算，通过试验对比，验证此方法的可行性。然后，建立不同区域铝型材的分析模型，并对比其隔声性能的优劣。本文的研究工作可为高速列车的车内噪声预测和低噪声改进设计等提供参考。

1  基础理论

1.1  阻尼参数测试

内损耗因子^[10]是重要的阻尼参数，定义为系统在单位频率内单位时间损耗的能量与平均储存能量之比。本文采用脉冲衰减法^[11-12]测量铝型材的内损耗因子。当结构件受到横向脉冲力作用时，其振动方程为

 (1)

式中：为给定激励力时的特解；为(m, n)模式的弯曲本征函数；w_mn为(m, n)模式简谐振动的角频率；相角j_mn及系数A_mn由结构件受振动时的初始条件确定；d_mn为相应的衰减因子；t为时间。

对试验测得的铝型材结构表面振动衰减信号V进行如下信号后处理。

1) 借助Butterworth带通滤波器，分离出对应各个简谐振动模式的自由阻尼振动：

   (2)

2) 将滤波后的振动信号先取平方，再取自然对数，得重构信号：

 (3)

3) 对重构信号进行多项式拟合，由拟合曲线的斜率确定相应的衰减因子2d_mn，进而得结构件的内损耗因子

              (4)

1.2  结构-声耦合法

采用基于结构-声耦合的有限元法研究铝型材的隔声性能。对流体声场的声传播，采用流体与结构单元形函数以及声学波动方程，同时考虑声学阻尼作用，可推导得流体区域内声场的有限元控制方程^[13]为

      (5)

式中：K_a为流体刚度矩阵；M_a为流体质量矩阵；C_a为流体阻尼矩阵；ω为振动圆频率；ρ₀为流体密度；p为节点声压；u为节点位移；A^T为流体与结构耦合矩阵的转置。

在流体与结构的交界面上，声压会对结构产生作用，类似可推导得结构振动的有限元控制方程为

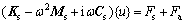        (6)

式中：K_s为结构刚度矩阵；M_s为结构质量矩阵；C_s为结构阻尼矩阵；F_s为结构外激励力；F_a为流体对结构的作用力。

式(5)和(6)描述了完全耦合的结构流体运动方程，用统一的矩阵形式可表示为

           (7)

式(7)所示为结构-声耦合系统的有限元控制方程，通过直接积分或基于模态空间的求解方法即可进一步得结构单元的位移和声学单元的声压。

2  铝型材样件的隔声性能

2.1  有限元建模

本试验所用铝型材样件的长×宽×高为1.25 m× 1.11 m×0.08 m，结构如图1所示，几何参数如表1所示。

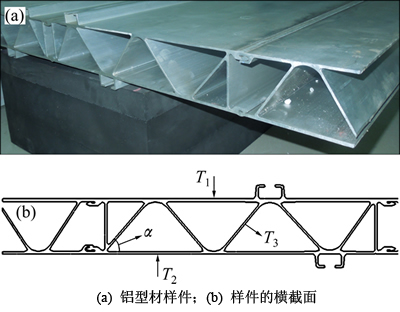
图1  铝型材样件示意图

Fig. 1  Schematic diagram of aluminum extrusion sample

表1  铝型材样件的几何特征参数

Table 1  Geometric parameters of aluminum extrusion sample

对铝型材样件进行有限元建模时，考虑到声桥结构对振动能量的传递有重要影响，二维建模会损失声桥的倒角特征，因此，本文采用三维建模，单元类型主要为6节点五面体和8节点六面体，如图2所示。仿真时弹性模量取E=72.4 GPa，泊松比υ=0.3，密度ρ=2 685 kg/m³。用锤击法进行铝型材模型的自由模态验证，前6阶模态频率的对比数据如表2所示。由表2可知：铝型材试件仿真频率的相对误差均在5%以内，说明有限元模型的精度较高，可用于后续的声学仿真计算。

2.2  内损耗因子

采用脉冲衰减法得到的测试结果如图3所示。内损耗因子是隔声量数值计算中的重要阻尼参数。由图3可见：铝型材的内损耗因子η随频率f的增加而逐渐减小，合理的取值范围为1.0×10^-3～4.5×10^-3。

图2  铝型材样件的有限元模型

Fig. 2  Finite element model of aluminum extrusion sample

表2  铝型材试件试验与仿真自由模态频率对比

Table 2  Free mode result comparison between experiment and simulation of aluminum extrusion sample

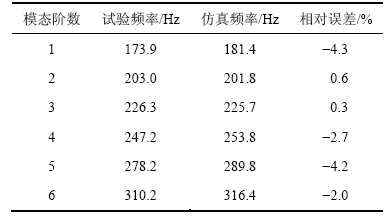
图3  铝型材的内损耗因子

Fig. 3  Internal loss factor of aluminum extrusion

2.3  隔声量仿真

采用结构-声耦合法进行铝型材样件的隔声量数值计算，仿真模型如图4所示。由图4可见：在铝型材有限元模型的两侧各自建立三维声腔网格，分别模拟发声室和接收室。由1/6波长原理可知^[14]，声腔单元的最大长度取28 cm，可满足2 000 Hz以内的计算精度。其中声腔的外表面均赋予自匹配层属性，用于完全吸收和辐射声功率，内表面与铝型材的结构网格定义为结构-声耦合面，形成声能的传递。仿真采用的原始边界条件为沿声桥纵向的4条边简支约束，激励源是入射侧的1 Pa混响声激励。铝型材样件的隔声量S_TL可由其定义公式直接计算：

               (8)

式中：W_i为入射声功率；W_o为辐射声功率。

通过结构-声耦合法计算得到的铝型材样件在1/3倍频程下的隔声结果如图5所示。由图5可见：隔声量曲线总体随频率的升高而稳定增长，其中在125和400 Hz附近存在2个明显的隔声谷，说明该中心频段内铝型材的隔声性能较差。而125 Hz以内隔声量较大可能是由边界条件引起。

图4  结构-声耦合法的仿真模型

Fig. 4  Simulation model of structure-sound coupling method

图5  结构-声耦合法计算得到的铝型材样件隔声量曲线

Fig. 5  Aluminum extrusion sample transmission loss curve calculated by structure-sound coupling method

2.4  试验验证

为验证结构-声耦合法的可靠性，本文作者设计相关隔声量试验并对铝型材样件进行测试。试验采用声强法并在满足国标规定的混响室-半消声室中进行，其中铝型材样件由铁块支座固定，四周采用油泥密封，如图6(a)所示。由图6(a)可见：发声室和接收室内分别布置有5个传声器和1个声强探头，铝型材的辐射侧表面被均分成25小块，每块区域的中心点定义为数据采集点。测试时在发声室内接入粉红噪声声源，待形成稳定的混响效果之后，记录各入射侧点的声压信号，并在接收室内近场定点采集双传声器的声压信号，移动轨迹如图6(b)所示。图6(b)中的蛇形路线，经信号后处理可得到有效辐射面积内的近场声强结果。

铝型材样件的试验隔声量计算公式如下：

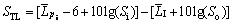      (9)

式中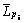：为发声室的声压级均值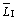；为接收室的声强级；S_i和S_o分别为入射侧和辐射侧的有效表面积。

图6  声强法隔声量试验示意图

Fig. 6  Schematic diagram of transmission loss experiment using sound intensity method

将试验得到的隔声量1/3倍频程曲线与仿真数值计算结果进行对比，如图7所示。由图7可见：仿真曲线与试验结果在隔声量的总体趋势上吻合较好，其中在200 Hz以下的中心频段，两者尚有一定的差距，主要受边界条件的影响。试验的边界条件较为复杂且具不确定性，而仿真施加的约束偏于理想化。仿真可能形成过约束，导致低频的铝型材结构振动较小，而隔声量偏大。为降低这一相对误差，可能须要释放部分节点的自由度，以寻求更接近试验约束的边界条件。相对而言，边界条件对200 Hz以上中心频段内的隔声量影响就较小，随着频段的升高，仿真与试验的相对误差越来越小，其中最大差值约为4 dB，出现在500 Hz处，属于工程应用中的合理误差范围。分析表明，结构-声耦合法可用于铝型材隔声性能的研究和分析。

3  不同区域铝型材的隔声性能

如前文所述，CRH3型高速列车的白车身结构主要由中空挤压铝型材构成。不同区域的铝型材设计要求不同，如地板铝型材不仅要承载乘客的质量，还须分担车下设备舱的部分质量，因此结构强度要求高；为了提升列车的空气动力学性能，侧墙和顶板铝型材等须设计成曲面结构。不同的设计要求导致铝型材的几何断面形状复杂多样，并会改变结构的声学性能，进而影响车内噪声的分布特征^[15]。因此，本文作者从CRH3型高速列车的原始几何模型中分别挑选出地板、侧面和顶部等不同区域的铝型材，并进一步研究其隔声性能。

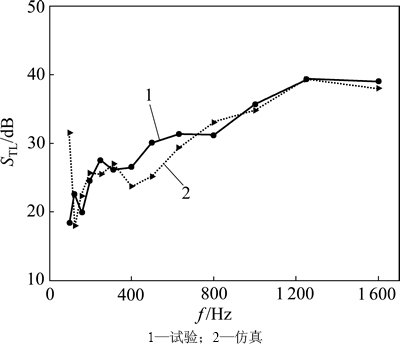
图7  铝型材样件的隔声量仿真与试验对比图

Fig. 7  Comparison of aluminum extrusion transmission loss acquired from numerical calculation and experiment

铝型材的几何模型和参数分别如图8和表3所示，其中L，W，H和σ分别代表铝型材的长度、宽度、板间高度和面密度。由表3可知：三者的主要区别为地板铝型材的面板平直且较厚，声桥布置较密及板间高度较大；侧墙和顶板铝型材的面板带有较小的弧度，声桥角度较小，几何断面形状较为相似，但后者的面板厚度更薄。有限元建模时同样采用三维网格，模型主要由6节点五面体和8节点六面体组成。

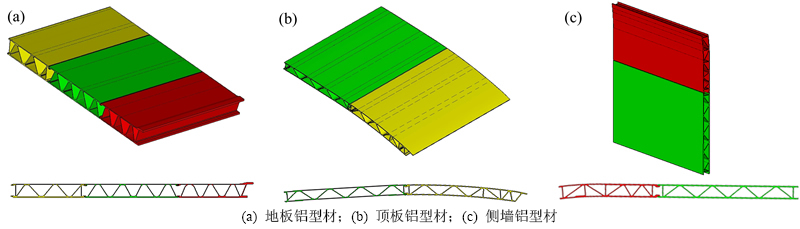
图8  不同区域铝型材的几何模型

Fig. 8  Geometry model of aluminum extruded panel from different areas

表3  不同区域铝型材的几何参数

Table 3  Geometric parameters of aluminum extruded panel from different areas

利用结构-声耦合法预测不同区域铝型材的隔声性能。由于部分铝型材结构表面的弯曲属性，建立声腔模型时也须作相应的调整，以保证数据映射的准确性。同时考虑到在整车装配状态下，铝型材之间是通过焊接而形成封闭的白车身结构，其边界条件较为模糊。为了避免过约束导致低频隔声量过大的情况，仿真时仅对铝型材的4个角落进行简支约束。

计算完成后，首先得到隔声量的等带宽频谱如图9(a)所示，仿真频段为50~1 800 Hz。由图9(a)可以看到：相比于结构简单的均质无限大板，铝型材的振动情况更加复杂，隔声规律也较为独特。其中地板、侧墙和顶板铝型材分别在95，119和117 Hz处得第一阶共振频率，在此之前隔声量主要受弯曲劲度控制，这与均质无限大板的隔声规律类似。三者的弯曲刚度由大到小分别为侧墙铝型材、顶板铝型材和地板铝型材。由于声激励为1 Pa的混响声源，声波在结构表面形成无归入射，导致铝型材在各阶整体和局部模态频率处均会产生隔声低谷，隔声量增长较为缓慢，“质量控制区”并不明显。且随频率的升高，隔声量曲线震荡越剧烈，从等带宽频谱上已很难继续进行比较。

因此，对比隔声量的1/3倍频程曲线，图9(b)所示为100~1 600 Hz中心频段内的仿真结果。由图9(b)可以看到：在400 Hz中心频段以下，由于边界条件对不同区域铝型材的约束效果不一样，隔声量的变化也没有明显的规律。在400 Hz以上，三者的隔声量从大到小依次为侧墙铝型材、地板铝型材和顶板铝型材。对比顶板与侧墙铝型材，两者的几何断面形状接近，但面密度分别为31.42和25.84 kg/m²，由质量定律可知相似结构的面密度较大则隔声量较大，因此，侧墙铝型材的隔声性能更好。顶板铝型材在500~1 250 Hz频段内有较宽的隔声谷，推测是因为其面板厚度较薄，结构在对应频段内的模态密度较高，导致辐射侧的声功率增加而使隔声量变差。对于地板铝型材，它的面密度达到33.20 kg/m²，是三者中最大的。但由于地板铝型材的板间高度为80 mm，明显高于侧墙和顶板铝型材的50 mm，声桥抑制结构面板的振动效果减弱，最终导致隔声量下降，其隔声性能仅次于侧墙铝型材的隔声性能，明显优于顶板铝型材的隔声性能。

通过对比可以发现：对于铝型材这类大型复杂的工程结构件，其隔声量特征频谱的“质量控制区”并不明显，且面密度不是判断隔声程度的唯一指标；一般情况下，适当增加声桥角度和面板厚度，可提升铝型材的面密度和结构强度，进而提升隔声量；增加板间距离则会给铝型材的隔声性能带来一定程度的恶化。工程应用中考虑到高速列车的轻量化等因素，铝型材自身的结构优化空间较小，多是结合新型吸声材料的应用以及内饰件声学包装的合理搭配等，对车内声场进行综合优化。

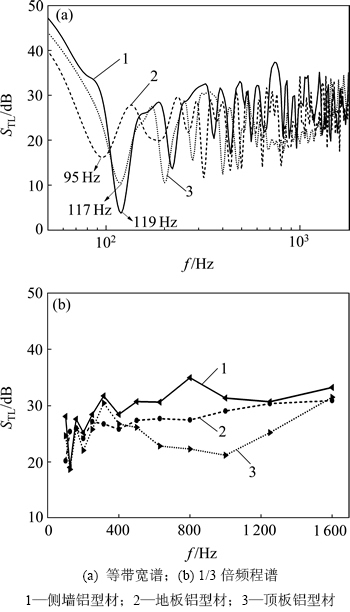
图9  不同区域铝型材的隔声量曲线

Fig. 9  Transmission loss curves of aluminum extruded panel from different areas

4  结论

1) 考虑结构阻尼性能对隔声量的影响，基于脉冲衰减法测量得到铝型材的内损耗因子，合理的取值范围为1.0×10^-3~4.5×10^-3，可用于隔声量的数值计算。

2) 采用结构-声耦合法计算得到铝型材样件在100~1 600 Hz中心频段内的隔声量，并通过试验对比发现两者一致性较好，说明仿真方法适用于铝型材的隔声性能研究。

3) 通过对比不同区域铝型材的隔声量发现，面密度最大的地板铝型材的隔声性能明显优于顶板铝型材的隔声性能，但次于侧墙铝型材的隔声性能。面密度不是判断铝型材隔声程度的唯一指标。

参考文献：

[1] 张曙光. 350 km·h^-1高速列车噪声机理、声源识别及控制[J]. 中国铁道科学. 2009, 30(1): 86-90.

ZHANG Shuguang. Noise mechanism, sound source localization and noise control of 350 km·h^-1 high-speed train[J]. China Railway Science, 2009, 30(1): 86-90.

[2] 王顺洪. 中国高速铁路发展及其经济影响分析[J]. 西南交通大学学报(社会科学版), 2010, 11(5): 65-69.

WANG Shunhong. The development of China’s high-speed railway and its economic influence[J]. Journal of Southwest Jiaotong University (Social Science), 2010, 11(5): 65-69.

[3] 张捷, 肖新标, 张玉梅, 等. 基于航空噪声指标的高速列车观光区噪声评价[J]. 机械工程学报. 2013, 49(16): 33-38.

ZHANG Jie, XIAO Xinbiao, ZHANG Yumei, et al. Noise evaluation in the tourist cabin of high-speed train by using aircraft noise criterion[J]. Journal of Mechanical Engineering, 2013, 49(16): 33-38.

[4] Wang J, LU Tianjian, Woodhouse J, et al. Sound transmission through lightweight double-leaf partitions: Theoretical modelling[J]. Journal of Sound and Vibration, 2005, 286(4/5): 817-847.

[5] XIN Fengxian, LU Tianjian. Sound radiation of orthogonally rib-stiffened sandwich structures with cavity absorption[J]. Composites Science and Technology, 2010, 70(15): 2198-2206.

[6] Kim S, Seo T. Sound insulation performance of honeycomb composite panel for a tilting train[J]. Transactions of the Korean Society of Mechanical Engineers A, 2010, 34(12): 1931-1936.

[7] Kim S, Seo T, Kim J T, et al. Sound-insulation design of aluminum extruded panel in next-generation high-speed train[J]. Transactions of the Korean Society of Mechanical Engineers A, 2011, 35(5): 567-574.

[8] Kim T M, Kim J T. Comparison study of sound transmission loss in high speed train[J]. International Journal of Railway, 2011, 4(1): 19-27.

[9] Xie G, Thompson D J, Jones C J C. A modelling approach for the vibro-acoustic behavior of aluminum extrusions used in railway vehicles[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 921-932.

[10] Bloss B C, Rao M D. Estimation of frequency-averaged loss factors by the power injection and the impulse response decay methods[J]. Journal of the Acoustical Society of America, 2005, 117(1): 240-249.

[11] 陈馨蕊，郝志勇，杨陈. 镁合金AZ31阻尼性能的实验研究[J]. 浙江大学学报(工学版), 2010, 44(1): 19-22.

CHEN Xinrui, HAO Zhiyong, YANG Chen. Experimental study on damping performance of magnesium alloy AZ31[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(1): 19-22.

[12] LUO Zhi, HAO Zhiyong, JIANG Bailing, et al. Micro arc oxidation and electrophoretic deposition effect on damping and sound transmission characteristics of AZ31B magnesium Alloy[J]. Journal of Central South University, 2014, 21(9): 3419-3425.

[13] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2012: 107-124.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Acoustic foundation[M]. Nanjing: Nanjing University Press, 2012: 107-124.

[14] Papadopoulos C I. Development of an optimized, standard- compliant procedure to calculate sound transmission loss: Numerical measurements[J]. Applied Acoustics, 2003, 64(11): 1069-1085.

[15] 陈旭, 王伊卿, 孙琨, 等. 高速列车车厢夹层板断面结构的多目标优化[J]. 西安交通大学学报, 2013, 47(1): 62-67.

CHEN Xu, WANG Yiqing, SUN Kun, et al. Multi-objective optimization for section of sandwich plate applied to high-speed train compartments[J]. Journal of Xi’an Jiaotong University, 2013, 47(1): 62-67.

(编辑  刘锦伟)

收稿日期：2014-11-28；修回日期：2015-01-18

基金项目(Foundation item)：国家高科技研究发展计划(863计划)资助项目(2011AA11A103) (Project(2011AA11A103) supported by the National High Technology Research and Development Program of China (863 Program))

通信作者：郑旭，讲师，从事高速列车减振降噪技术研究；E-mail: zhengxu@zju.edu.cn