J. Cent. South Univ. (2016) 23: 834-840

DOI: 10.1007/s11771-016-3130-0

L₁ adaptive controller of nonlinear reference system in presence of unmatched uncertainties

SONG Hai-tao(宋海涛)^{1, 2}, ZHANG Tao(张涛)², ZHANG Guo-liang(张国良)¹

1. The Third Department, High-Tech Institute of Xi’an, Xi’an 710025, China;

2. Department of Automation, School of Information Science and Technology, Tsinghua University, Beijing 100084, China

 Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: an extension of L₁ adaptive control is proposed for the unmatched uncertain nonlinear system with the nonlinear reference system that defines the performance specifications. The control law adapts fast and tracks the reference system with the guaranteed robustness and transient performance in the presence of unmatched uncertainties. The interval analysis is used to build the quasi-linear parameter-varying model of unmatched nonlinear system, and the robust stability of the proposed controller is addressed by sum of squares programming. The transient performance analysis shows that within the limit of hardware a large adaption gain can improve the asymptotic tracking performance. Simulation results are provided to demonstrate the theoretical findings of the proposed controller.

Key words: L₁ adaptive controller; unmatched uncertainties; robustness; transient performance

1 Introduction

Unmatched uncertain system is an important branch of nonlinear system, which is common in aerospace [1-2], robot [3] and missile [4]. For the controller design, both robustness and transient performance should be taken into consideration. However, the common nonlinear design methods, such as sliding-mode, feedback linearization, backstepping, composite nonlinear feedback control and so on, only ensure partial system performance. Sliding-mode control is robust to matched uncertainties, whereas it is lack of robustness for unmatched uncertainties [5]. Feedback linearization does not have the robustness for uncertainties [6-7]. Backstepping method has the problem of explosion of terms [8-9], and it cannot reflect the transient performance [10]. The composite nonlinear feedback control and its modified methods achieve fast and accurate tracking for linear disturbed systems, but the disturbance is assumed to be constant and the uncertainties are not considered [11]. Therefore, all these mentioned methods cannot achieve the controller design for unmatched uncertain system with both guaranteed robustness and transient performance.

For the linear time invariant (LTI) system, adaptive control was a suitable method to achieve improved robustness and asymptotic stability [12]. The simple adaptive control (SAC) methodology was firstly introduced by Sobel et al [13] and had been developed by ULRICH et al [14]. Successful implementations of SAC in various domains of application have been presented over the past two decades. A passification- based adaptive control approach for the SISO (single input single output) uncertain system was studied in Ref. [15]. However, these methods cannot be applied to the nonlinear MIMO (multiple input multiple output) system with unmatched uncertainties.

Interestingly, L₁ adaptive control, which was proposed by Cao and Hovakimyan in Refs. [16-17], can guarantee robustness and transient performance in the process of high-speed adaptation. Based on the structure of indirect model reference adaptive controller, L₁ adaptive controller estimates the system uncertainties and defines the control signals to eliminate the influence of uncertainties. Unlike the conventional adaptive controllers, L₁ adaptive controller adapts fast, leading to the asymptotic tracking with bounded away from zero and positive time-delay stability margin that make it be widely applied to a variety of vehicles, such as aircraft, missile, and unmanned aerial vehicle [18-19].

L₁ adaptive control has various forms for different study objects. For example, the research objects were extended from linear system [16] to nonlinear system [20], and non-affine nonlinear system [21]. Moreover, the uncertainties were treated as matched initially [22],and then unmatched [23], and both coexisted [24]. Furthermore, linear system or nonlinear one was chosen as the reference system, while the nonlinear one reflected the essence of control system better. In Ref. [20], L₁ adaptive controller with the nonlinear reference system was presented for matched uncertain nonlinear systems. However, to the best of our knowledge, no attempts have been made in the L₁ adaptive control of nonlinear reference system with unmatched uncertainties.

Therefore, this work provides an extension of L₁ adaptive control that can accommodate the nonlinear reference behaviors in the presence of unmatched uncertainties. Based on the idea of L₁ adaptive control, the new controller is designed considering the model specialty of study object. Then, the robust stability and transient performance are analyzed respectively. The quasi-linear parameter-varying (qLPV) model of unmatched nonlinear system is adopted for the robust stability analysis using sum of squares (SOS) programming. The transient performance analysis shows that within the limit of hardware the large adaption gain can improve the asymptotic tracking performance.

2 Problem formulation

Consider the unmatched uncertain nonlinear MIMO plant

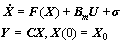                             (1)

where X∈Rⁿ is the system state; U∈R^m(m≤n) is the control input; Y∈R^k is the output; F(X)∈Rⁿ and U_m∈R^n×m are known functions; and 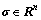 is the unmatched uncertainty including model uncertainties and disturbances.

Assumption 1: All the system states are available for measurement.

Assumption 2: The unmatched uncertainty 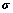 and its derivative  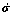are continuous and bounded, that is, there exist positive constants  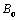and 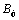 such that

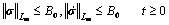                       (2)

where the definition of 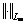is presented in Ref. [25].

The control objective is to design an adaptive state feedback controller such that the state X of the real system tracks the state X_ref of the following reference system as soon as possible with desired transient performance

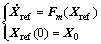                               (3)

3 L₁ adaptive controller design

This section presents an L₁ adaptive controller for system (1) to accommodate the nonlinear reference behaviors in the presence of unmatched uncertainties that can be quickly estimated. The output of a low pass filter is defined as control input compensating the influence of unmatched uncertainties. The design of L₁ adaptive controller follows the procedure described in Refs. [20, 23]. Generally, L₁ adaptive controller contains three parts: state predictor, adaptation law, and control law that are shown in Fig. 1.

3.1 State predictor

The state predictor is defined as

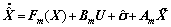                      (4)

where 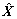 is the state of state predictor with 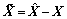  is the state predictor error;  is the adaptive estimate of s; and A_m is any Hurwitz matrix that defines the desired convergence properties of error dynamics.

3.2 Adaptation law

 is updated by the adaptation law [2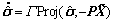5]

                           (5)

where Γ>0 is the adaptation gain;

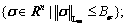 and 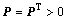 is the solution of the algebraic Lyapunov equation:

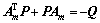                               (6)

for arbitrary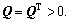

The projection operator 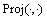ensures the adaptive estimate  is bounded. Then, this in turn ensures that the control signal and system states remain bounded [25].

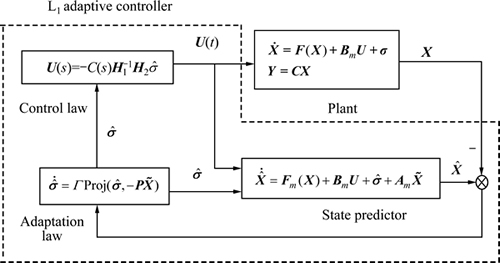
Fig. 1 Structure of L₁ adaptive controller

3.3 L₁ adaptive control law

The adaptive feedback signal is defined as

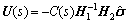                           (7)

where a low pass filter C(s) is strictly proper and stable with C(0)=1, and

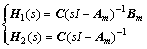                           (8)

Remark 1: H₁(s) is the reference transfer function from the matched input, which is simply how the outputs are affected by the inputs. H₂(s) is the reference transfer function from unmatched input, which is how the outputs are affected in input directions that are orthogonal to the directions defined by B_m. This design of creating one term in the control signal u by taking the estimated unmatched error and feeding it through the inverse of the matched transfer function 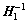 and the unmatched transfer function H₂(s), creates a way to compensate for unmatched uncertainties [26]. Therefore, the term  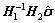connotes the predicted effect of the unmatched uncertainties on the input of the plant. The low pass filter C(s) serves to attenuate unwanted high frequency components in the actuation signal, which reflects the robustness.

For the performance analysis, it is needed to ensure that: 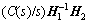 is strictly proper and stable. Therefore, this requires a careful construction of  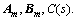A first-order low pass filter of the form is the simplest choice for the filter as

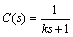                                   (9)

where k>0 is a design parameter.

4 Robust stability analysis

The qLPV model guarantees the nonlinear characteristic of system and ensures that the equilibrium point of uncertain nonlinear systems is fixed for all allowable parameters, and it seeks a balance between model accuracy and algorithm complexity [27]. Therefore, the qLPV model is built by using interval analysis [28] to analyze the robust stability. And then, the robustness stability is verified by SOS programming [27].

4.1 qLPV model

The model (1) can be rewritten as

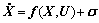                              (10)

The uncertainties  are assumed to be bounded with known bounds 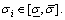 X_c, U_c, and  are the midpoints of [X], [U], and 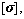 respectively; and the scheduling parameter vector is defined  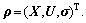The qLPV model is based on the mean value inclusion function [29]. The mean value inclusion function [f_c] is given by

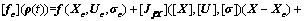
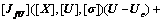
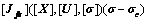                   (11)

where [J_f] is an inclusion function of J_f=(J_fX, J_fU, J_fσ)^T with

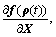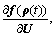J_fX= J_fU= J_fσ=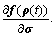

Since 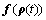 is independent of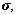 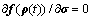  and (11) can be rewritten as

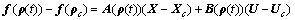 (12)

where 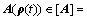[J_fX], 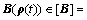[J_fU].

Choosing 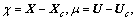 then the system is

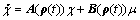                               (13)

Such system is the qLPV model of (1) around the equilibrium point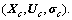

4.2 Robust stability

From Eq. (13), we consider the qLPV model

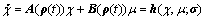               (14)

where 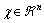 is state vector;  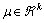is the input; and the matrices A and B are polynomial in  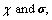respectively. A domain of the state space that contains the origin for performance analysis is defined by

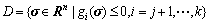              (15)

where g_i are polynomial in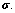

The robust stability is for the unforced dynamical system with input μ=0 of the qLPV model (14):

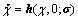                                (16)

The equilibrium point of model (14) is assumed to be 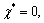 and the function h is assumed to be smooth so that the solutions are existent and unique.

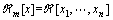 abbreviated as  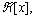is the commutative ring of multivariable polynomials in x₁, …, x_n of maximum degree m. A polynomial p(x) is said to be an SOS when it can be written as [27]

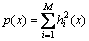                                  (17)

where 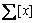 denotes the set of SOS polynomials of fixed degree.  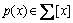if and only if there exists a vector of monomials Z(x) and a positive semidefinite matrix W such that

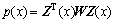                               (18)

Then, this formulation allows SOS decompositions to be computed using semidefinite programming. We use the SOS decompositions to construct the Lyapunov function for model (16).

Programme 1 [27]: Select even integers a, m_i, n_i>0 and search for a polynomial 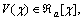 where V(0)=0, SOS polynomials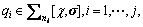 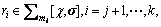  and positive definite functions  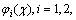such that

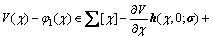
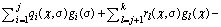
Then, χ^* is a robustly stable equilibrium point and V(χ) is a Lyapunov function for model (16).

The functions φ_i(χ) have the form as

Remark 2: If programme 1 returns an infeasible solution, we can increase a, m_i, n_i. However, the computational cost may also do so. ANDERSON and PAPACHRISTODOLOU [30] proposed a method for reducing the computational burden of high-order SOS programming based on system decomposition.

5 Transient performance analysis

Lemma 1: Consider the system in Eq. (1) with the L₁ adaptive controller in Eqs. (4), (5), and (7). The following inequality holds:

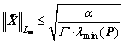                           (19)

where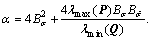

Proof: The predictor error dynamics is obtained using Eqs. (1) and (4) as

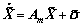                              (20)

Let 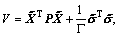 where 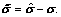 Compute the time derivative of V using Eq. (5):

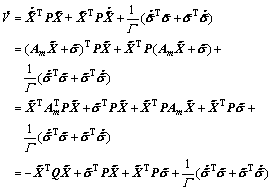
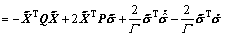          (21)

By the definition of the projection operator 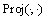 in Ref. [25]

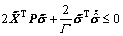                            (22)

Then, we have

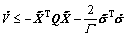                          (23)

According to the Assumption 2, the bound of 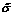 is 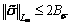 that leads to

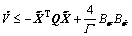                         (24)

If at time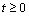

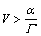                                       (25)

Then, we get

                           (26)

Hence,

                 (27)

Therefore, it follows inequality (24) that

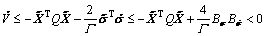     (28)

We know that

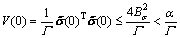                  (29)

From Eq. (28), 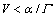 for any t≥0 that is in contradiction with Eq. (25). Therefore, we verify that

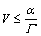                                       (30)

Since 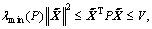 then

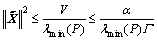                      (31)

That implies

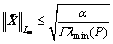                               (32)

Remark 3: From lemma 1 we know the state predictor error has bound that is inversely proportional to adaptation gain. This means that within the limit of hardware the asymptotic tracking performance can be improved by increasing the adaption gain.

Lemma 2: The state predictor error has limit as .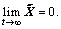

Proof: From Lemma 1, the state predictor error has bound and 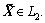 Further, from Eq. (20), we know  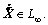Then we apply Barbalat’s lemma [31] to conclude convergence of  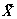to zero.

6 Simulation results

This section demonstrates the performance of the proposed L₁ adaptive controller using a numerical simulation example. Consider an unmatched nonlinear system

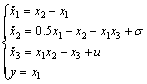
with 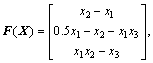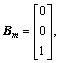C=[1 0 0], and  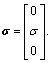The initial states are X₀=[0.5 0.3 0.3]^T, the adaptation gain is Γ=10⁵, the matrix A_m in the state predictor is  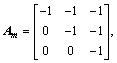and the low pass filter is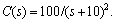

Two kinds of uncertainties are chosen to test the controller performance without any retuning of the controller. Firstly, the uncertainty is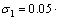  

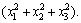
To verify the advantages of the proposed controller, the L₁ adaptive controller for nonlinear time-varying reference systems (L₁-matched) [20] and the SAC presented in Ref. [14] are used for comparisons.

The state predictor errors are shown in Fig. 2. The state tracking error between real system and reference system is shown in Fig. 3. It is found that the proposed controller is stable. And lemma 1 and lemma 2 are verified by the results. The error curves of L₁-matched and SAC are divergent and irregular. Therefore, these two methods cannot solve the tracking problem for nonlinear reference system in the presence of unmatched uncertainties, let alone the robustness and transient performance.

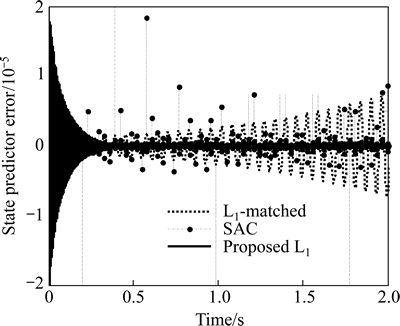
Fig. 2 State predictor errors 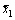 for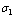

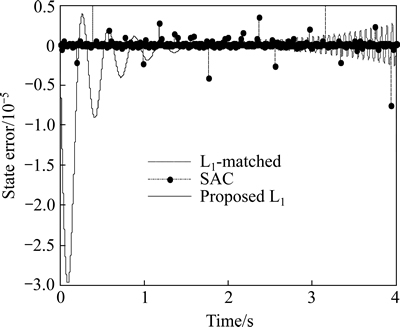
Fig. 3 State tracking error of 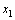 for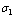

The second uncertainty is  with the same controller. The state predictor errors and state tracking error between real system and reference system are shown in Figs. 4 and 5. It is noted that the system response and control signal behave as expected. Compared with the first uncertainty, although the signals trajectories of the second case are different, the errors have corresponding bounds. The simulation results verify that the proposed L₁ adaptive controller guarantees robustness and transient performance for the different kinds of uncertainties.

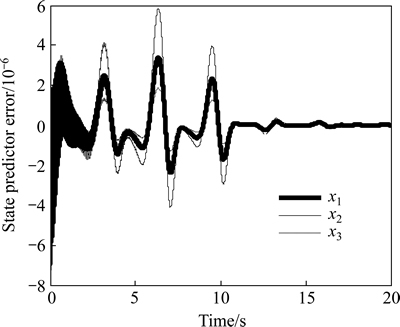
Fig. 4 State predictor errors for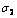

Fig. 5 State tracking error of x₁ for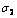

7 Conclusions

1) L₁ adaptive control is extended to the unmatched uncertain nonlinear system with nonlinear reference system.

2) The proposed controller guarantees robustness and transient performance in the presence of unmatched uncertainties.

3) SOS programming of qLPV system built by interval analysis has been used for robustness stability analysis. The transient performance analysis shows that within the limit of hardware large adaption gain can improve the asymptotic tracking performance.

4) L₁ adaptive control discusses tracking error and control error in the form of L₁ or L_∞ norms that represent the overall performance. However, the direct relationship between controller parameters and system performance has not been established analytically, which is the future work.

References

[1] SU Shan-wei, LIN Yan. Robust output tracking control for a velocity-sensorless vertical take-off and landing aircraft with input disturbances and unmatched uncertainties [J]. International Journal of Robust and Nonlinear Control, 2013, 23(11): 1198-1213.

[2] LEMAN T, XARGAY E, DULLERUD G, HOVAKIMYAN N, WENDEL T. L₁ adaptive control augmentation system for the X-48B aircraft [C]// AIAA Guidance, Navigation, and Control Conference. Chicago, Illinois: AIAA, 2009, DOI: 10.2514/6.2009-5619.

[3] LI Yong-ming, TONG Shao-cheng, LI Tie-shan. Fuzzy adaptive dynamic surface control for a single-link flexible-joint robot [J]. Nonlinear Dynamics, 2012, 70(3): 2035-2048.

[4] HOU Ming-zhe, LIANG Xiao-ling, DUAN Guang-ren. Adaptive block dynamic surface control for integrated missile guidance and autopilot [J]. Chinese Journal of Aeronautics, 2013, 26(3): 741-750.

[5] KWAN C M. Sliding mode control of linear systems with mismatched uncertainties [J]. Automatica, 1995, 31(2): 303-307.

[6] LI Yong-ming, TONG Shao-cheng, LI Tie-shan. Adaptive fuzzy backstepping control of static var compensator based on state observer [J]. Nonlinear Dynamics, 2013, 73(1/2): 133-142.

[7] SLOTINE J J, LI Wei-ping. Applied nonlinear control [M]. New Jersey: Prentice Hall, 1991.

[8] LI Jin-hui, LI Jie, YU Pei-chang, WANG Lian-chun. Adaptive backstepping control for levitation system with load uncertainties and external disturbances [J]. Journal of Central South University, 2014, 21(12): 4478-4488.

[9] XIONG Gen-liang, XIE Zong-wu, HUANG Jian-bin, LIU Hong, JIANG Zai-nan, SUN Kui. Dynamic surface control-backstepping based impedance control for 5-DOF flexible joint robots [J]. Journal of Central South University of Technology, 2010, 17(4): 807-815.

[10] XU Yin-yin, TONG Shao-cheng, LI Yong-ming. Adaptive fuzzy fault-tolerant control of static var compensator based on dynamic surface control technique [J]. Nonlinear Dynamics, 2013, 73(3): 2013-2023.

[11] MOBAYEN S, MAJD V J. Robust tracking control method based on composite nonlinear feedback technique for linear systems with time-varying uncertain parameters and disturbances [J]. Nonlinear Dynamics, 2012, 70(1): 171-180.

[12] BARKANA I. Gain conditions and convergence of simple adaptive control [J]. International Journal of Adaptive Control and Signal Processing, 2005, 19(1): 13-40.

[13] SOBEL K, KAUFMAN H, MABIUS L. Implicit adaptive control for a class of MIMO systems [J]. IEEE Transactions on Aerospace and Electronic Systems, 1982, AES-18(5): 576-590.

[14] ULRICH S, SASIADEK J Z, BARKANA I. Modeling and direct adaptive control of a flexible-joint manipulator [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 25-39.

[15] FRADKOV A L, ANDRIEVSKY B, PEAUCELLE D. Adaptive control design and experiments for LAAS “helicopter” benchmark [J]. European Journal of Control, 2008, 14(4): 329-339.

[16] CAO Cheng-yu, HOVAKIMYAN N. Design and analysis of a novel L₁ adaptive controller, Part I: Control signal and asymptotic stability [C]// American Control Conference. Minneapolis, Minnesota: IEEE, 2006: 3397-3402.

[17] CAO Cheng-yu, HOVAKIMYAN N. Design and analysis of a novel L₁ adaptive controller, Part II: Guaranteed transient performance [C]// American Control Conference. Minneapolis, Minnesota: IEEE, 2006: 3403-3408.

[18] ERDOS D, SHIMA T, KHARISOV E, HOVAKIMYAN N. L₁ adaptive control integrated missile autopilot and guidance [C]// AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota: AIAA, 2012, DOI: 10.2514/6.2012-4465.

[19] MALLIKARJUNAN S, BILL N, KHARISOV E, XARGAY E, HOVAKIMYAN N, CAO Cheng-yu. L₁ adaptive controller for attitude control of multirotors [C]// AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota: AIAA, 2012, DOI: 10.2514/6.2012-4831.

[20] WANG Xiao-feng, HOVAKIMYAN N. L₁ adaptive controller for nonlinear time-varying reference systems [J]. Systems & Control Letters, 2012, 61(4): 455-463.

[21] LUO Jie, CAO Cheng-yu, YANG Qin-min. L₁ adaptive controller for a class of non-affine multi-input multi-output nonlinear systems [J]. International Journal of Control, 2013, 86(2): 348-359.

[22] LEE K W, SINGH S N. Multi-input submarine control via L₁ adaptive feedback despite uncertainties [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2014, 228(5): 330-347.

[23] CAO Cheng-yu, HOVAKIMYAN N. L₁ adaptive controller for multi-input multi-output systems in the presence of unmatched disturbances [C]// American Control Conference. Washington, USA: IEEE, 2008: 4105-4110.

[24] XARGAY E, HOVAKIMYAN N, CAO Cheng-yu. L₁ adaptive controller for multi-input multi-output systems in the presence of nonlinear unmatched uncertainties[C]// American Control Conference. MD, USA: IEEE, 2010: 874-879.

[25] YOO S J, HOVAKIMYAN N, CAO Cheng-yu. Decentralised L₁ adaptive control for large-scale non-linear systems with interconnected unmodelled dynamics [J]. IET Control Theory & Applications, 2010, 4(10): 1972-1988.

[26] PETERSON A, STROM K, ROBERTSSON A, JOHANSSON R. Augmenting L₁ adaptive control of piecewise constant type to a fighter aircraft. Performance and robustness evaluation for rapid maneuvering [C]// AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota: AIAA, 2012.

[27] HANSEN E R. Global optimization using interval analysis [M]. New York: CRC Press Inc, 2004.

[28] RAISSI T, VIDEAU G, ZOLGHADRI A. Interval observer design for consistency checks of nonlinear continuous-time systems [J]. Automatica, 2010, 46(3): 518-527.

[29] ANDERSON J, PAPACHRISTODOULOU A. Robust nonlinear stability and performance analysis of an F/A-18 aircraft model using sum of squares programming [J]. International Journal of Robust and Nonlinear Control, 2013, 23(10): 1099-1114.

[30] ANDERSON J, PAPACHRISTODOULOU A. A decomposition technique for nonlinear dynamical system analysis [J]. IEEE Transactions on Automatic Control, 2012, 57(6): 1516-1521.

[31] TAO G. A simple alternative to the Barbalat lemma [J]. IEEE Transactions on Automatic Control, 1997, 42(5): 698.

(Edited by DENG Lü-xiang)

Received date: 2015-01-12; Accepted date: 2015-06-10

Corresponding author: SONG Hai-tao, PhD; Tel: +86-18911302963; E-mail: songht1018@163.com