J. Cent. South Univ. Technol. (2011) 18: 1693-1699

DOI: 10.1007/s11771-011-0890-4

Critical crack tip opening displacement of different strength concrete

WANG Bing(王冰)^{1, 2}, ZHANG Xiu-fang(张秀芳)¹, DAI Jian-guo(戴建国)³, XU Shi-lang(徐世烺)^{1, 4}

1. Civil Engineering Institute, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116023, China;

2. The Communications Research Institute of Liaoning Province, Shenyang 110015, China;

3. Department of Civil and Structural Engineering, The Hong Kong Polytechnic University,Hung Hom, Kowloon, Hong Kong, China;

4. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Critical crack tip opening displacement (CTOD_c) of concrete using experimental and analytical evaluation with seven different compressive strengths ranging from 30 up to 150 MPa was studied based on two types of fracture tests: three-point bending (TPB) and wedge splitting (WS). In the tests, the values of CTOD_c were experimentally recorded using a novel technique, in which fiber Bragg grating (FBG) sensors were used, and two traditional techniques, in which strain gauges and clip gauges were deployed. The values of CTOD_c of tested concrete were also predicted using two existing analytical formulae proposed by JENQ & SHAH and XU, respectively. It is found that the values of CTOD_c obtained by both experimental measurements and analytical formulae exhibit a negligible variation as the compressive strength of concrete increases, and the test geometry adopted has little impact on the value of CTOD_c. Regarding the experimental measurement of CTOD_c, the clip gauge method generally leads to a larger value of CTOD_c and shows a more significant scatter as compared with the other two methods, while the strain gauge method leads to a slightly lower CTOD_c as compared with the FBG sensor method. The analytical formula proposed by JENQ and SHAH is found to generally lead to an overestimation, while the analytical formula proposed by XU shows a good accuracy.

Key words: critical crack tip opening displacement (CTOD_c); fiber Bragg grating (FBG) sensors; three-point bending (TPB) tests; wedge splitting (WS) tests; high strength; concrete

1 Introduction

High strength concrete (HSC) is different from normal strength concrete (NSC) in terms of its elastic modulus, brittleness, fatigue life, ductility, cracking behavior, etc. Consequently, it is essential to distinguish the crack formation and fracture characteristics featured in HSC from those in NSC. Critical crack tip opening displacement (CTOD_c) is a good indicator of fracture properties of concrete materials and usually serves as an index to reflect the crack development in plastic fracture analysis. Some recent study on the CTOD_c has been focused on the influences of concrete strength, coarse aggregate type and size, curing condition, water to binder ratio and silica fume content [1-7]. Regarding the coarse aggregate type and size, some studies revealed that the crack resistance of concrete consisting of gravel was higher than that of concrete consisting of limestone, and an increase in the size of coarse aggregates led to an increase in CTOD_c. The possible reason for this was that coarse aggregates were able to provide more bridging effects in concrete [1-3]. On the contrary, LIN et al [4] reported that the size of coarse aggregates had a very small influence on the CTOD_c, which just varied slightly with the curing age under a wet curing condition although the compressive strength of concrete kept increasing. As for the influence of water-to-binder ratio and silica fume content, BARR et al [5] and NAVALURKAR et al [6] found that a smaller CTOD_c and a steeper ascending branch of the load vs crack mouth opening displacement (CMOD), and the load vs crack tip opening displacement (CTOD) curves were usually observed in case of a smaller water-to-binder ratio when the same content of silica fume was used in concrete. ZHAO and XU [7] concluded that the critical crack propagation length and the CTOD_c decreased with the decrease of the water-to-binder ratio when the maximum size of coarse aggregates was kept constant. ZHOU et al [2] reported that the CTOD_c increased with the silica fume content in concrete. On the contrary, LIN et al [4] reported that the CTOD_c was hardly affected by the silica fume content in concrete. Therefore, it remains quite controversial on how the CTOD_c changes with the water-to-binder ratio and the silica fume content.

Some attempts have been made in the past few years to evaluate the CTOD_c by analytical approaches as well as various experimental techniques including the use of laser speckle interferometry [8-10], clip gauges, strain gauges [10-11] and linear variable displacement transducers (LVDT). Recently, the application of fiber optic sensors to evaluate the CTOD_c has gained increasing popularity. ANSARI and NAVALURKAR [12] measured the CTOD_c of steel fiber reinforced concrete beams by embedding intensity-based fiber optic sensors in the beams. They suggested that the diameter of fiber- optic loop should be larger than 25.4 mm to avoid any permanent damage of fibers. CHEN et al [13] developed a new intensity-based fiber optic sensor, by which the intensity variation of the speckle patterns caused by the mode redistribution was evaluated, so that the CTOD_c, the internal strains and the deformations of cementitious composites could be identified. LEE et al [14] employed polarization-maintaining optical fibers to determine the CTOD_c in cementitious composites. The gauge length of the optical fiber was required to be long enough to ensure high sensitivity in measurement. YUAN and ANSARI [15] used embedded white light interferometer fiber optic sensors to monitor the CTOD_c in their fracture tests. Such interferometer techniques were capable of measuring a displacement resolving power with a high resolution up to 1 μm, but the accuracy of the measurement was very sensitive to the applied fiber optic gauge length. LEUNG et al [16] fixed a simple ‘zig-zag’ sensor at the bottom of a bridge deck to measure the cracks in concrete and found that such sensors had a high sensitivity of about 0.1 mm. LI et al [17] measured the tensile stress vs CTOD curves of concrete containing a semi-elliptical surface crack using fiber optic sensors. However, in their tests, the sensor was mounted at 5 mm from the crack tip, considering the difficulty in locating the embedded sensors right at the real tip of the crack. ZHANG and ANSARI [18] employed a speckle-based fiber optic sensor to estimate the CTOD_c based on captured images by means of a digital or video camera. It was discovered from their tests that such a sensor usually had a high signal-to-noise ratio and was involved with complicated theoretical derivations. Moreover, the gauge length of fibers may be required to even be as long as   1 m in order to improve the noise ratio.

This work aims to investigate the fracture properties of concrete with a compressive strength varying from 30 to 150 MPa using different test and measurement methods. Two types of tests, three-point bending (TPB) test and wedge splitting (WS) test, were also used to observe the effects of specimen geometry on the value of CTOD_c of concrete with different strength grades. Another objective of this work is to compare the validity of different methods for measuring the CTOD_c. Three different measurement methods, including fiber Bragg gating sensors (FBG), strain gauge and clip gauge, were employed to monitor the CTOD_c in concrete fracture experiments. A bare FBG sensor was attached on the surface of each testing specimen to avoid introducing any damage into the interior concrete. On the other hand, the deviation of the sensor location and the damage of the sensor possibly induced by the vibration during the casting of specimens could be avoided. Despite this simple installation, the sensor could be fixed at a location very close to the tip of the artificial crack. The final objective of this work is to observe if existing analytical formulae, such as JENQ and SHAH’s analytical formula [19] and XU’s modified analytical formula [20], can predict the CTOD_c through comparing with the obtained benchmark database.

2 Experimental

2.1 Materials

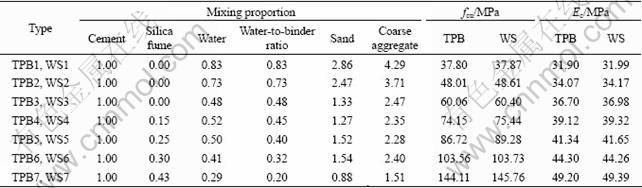
The concrete used had seven different types of mixing proportions as indicated in Table 1. The maximum size of the coarse aggregate was 20 mm. The cube (150 mm × 150 mm × 150 mm) compressive strength and elastic modulus of specimens at testing time are also presented in Table 1.

2.2 Test specimens

The test involves two types of geometry specimens, including three-point bending (TPB) specimens and wedge splitting (WS) specimens. A total of 84 specimens were cast in the tests. Each geometry type had 42 specimens prepared with seven different mixing proportions (see Table 1) and each kind of mixing proportion had six identical specimens. Figures 1(a) and 1(b) show the schematic diagrams of concrete specimens for TPB tests and WS tests, respectively. The notch in the specimens was formed using a greased steel plate of    3 mm in thickness. The ratio of the initial notch length to the whole depth of the specimens was 0.4 for both types of tests. The dimensions of the TPB specimens were      1 000 mm (length)×200 mm (depth)×120 mm (thickness). The clear span of the TPB beams was 800 mm.

The dimensions of the WS specimens were 200 mm (width) × 200 mm (thickness) × 230 mm (depth). The wedge angle, θ, of the loading device was 15°, as indicated in Fig.1(b). The horizontal component, P_H, of the contact force, which is transferred by the wedge loading frame, can be written as

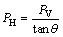                                                                   (1)

where P_V is the vertical component of the contact force.

Table 1 Mixing proportions, compressive strength f_cu and elastic modulus E_c of concrete

As seen in Fig.1(b), the moment at the crack tip consists of two components: the effective moment M_H produced by horizontal force P_H and the additional bending moment M_V produced by vertical force P_V:

M=M_H+M_V                                                                    (2)

where

M_H=P_Ha₀                                                                       (3)

                                      (4)

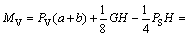
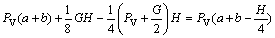  (5)

where a₀ is the length of the pre-notch, H is the width, D is the depth, G is the self-weight of the WS specimens, and P_S is the reaction force at each support.

M_V=0 means that there is no additional bending moment at the crack tip. However, if M_V <0 or M_V>0, additional bending moment will suppress or benefit the crack propagation, leading to a lower or larger measured value of CTOD_c. In the current tests (H=200 mm, a=  25 mm, b=40 mm), M_V =15P_H tan15° ≈4.02P_H and M_H = 80P_H. Compared with M_H, M_V is much smaller. Accordingly, the influence of the additional bending moment on the measurement of CTOD_c is ignored in the analysis.

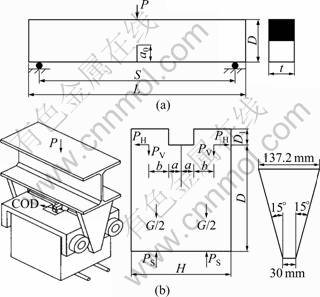
Fig.1 Configurations of three-point bending notched beam (a) and wedge splitting specimen (b)

2.3 CTOD_c measurement by strain gauges and clip gauges

A total of three strain gauges were attached onto the surface of each TPB and WS specimens at the height of crack tip to measure the initiation and propagation of the crack. Two gauges were symmetrically attached as closely as possible to the tip of the crack (see Figs.2(a) and 2(b)) to form a full-bridge electro circuit to monitor the crack initiation, and the remained one was attached right at the location of crack tip to measure the CTOD_c (see Fig.2(b)).

Two clip gauges were installed on the specimen (see Figs.2(a) and 2(b)). One was used to measure the critical crack mouth opening displacement (CMOD_c), and the

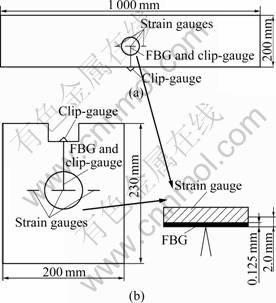
Fig.2 Illustrations of strain gauges, clip gauges and FBG sensors in TPB (a) and WS specimens (b)

other was used to measure the critical crack tip opening displacement (CTOD_c).

2.4 CTOD_c measurement by FBG sensors

Different from the regular fiber core, fiber Bragg grating is obtained by creating periodic modulation in the core of an optical fiber [21]. When broadband light passes through the grating in the core of the optical fiber, the light at a particular wavelength, called the Bragg wavelength, will be reflected back due to the difference in refraction indices (see Fig.3). The light reflected will be in an equal phase and amplification. The Bragg wavelength is easily affected by any change in external environments, (i.e. a wavelength shift). Any temperature, strain, or stress that influences the FBG is simply proportional to the wavelength shift and can be directly determined. The Bragg wavelength of the resonance condition in FBG is expressed as

λ_B=2nΛ                                               (6)

where λ_B is the Bragg wavelength, n is the effective refractive index of the core, and Λ is the grating period.

The relationship among the wavelength shift, Δλ_B, and the temperature shift, ΔT, and the longitudinal strain change, Δε, is given as

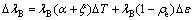                         (7)

where α is the thermal expansion coefficient, ξ is the thermal optic coefficient, ρ_e is the effective photo-elastic constant of the fiber core material.

Once the Δε is obtained, the CTOD_c can be determined by multiplying Δε with the gauge length.

In the test, as shown in Fig.2(a) and Fig.2(b), a bare FBG sensor was attached right at the tip of the notch of the TPB and WS specimens. The FBG sensor had a grating of 10 mm in length. The Bragg wavelength is in between 1 520 nm and 1 560 nm with a refractive index of 1.62 and a scanning resolution of 1 pm.

2.5 Test procedures

All tests were carried out according to “China Norm for Fracture Test of Hydraulic Concrete (DT/T 5332- 2005)” [22] under a closed-loop servo-controlled MTS structural loading system of 30 t in capacity. The loading speed was 0.02 mm/min. The information of FBG sensors was collected by an SI 425 optical sensing interrogator (16 channels). Other data were recorded by a German IMC Cronos PL dynamic data acquisition system (64 channels).

3 Analytical formulas

3.1 Determination of CTOD_c from JENQ and SHAH’s equation

Besides the critical stress intensity factor, 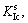 the critical crack tip opening displacement CTOD_c (D_c,T) was introduced as a fracture governing parameter in the two-parameter fracture equation proposed by JENQ and SHAH [19]:

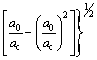                                             (8)

a_c is calculated according to the expressions used in double-K fracture model proposed by XU and REINHARDT, which is given by Eq.(9) for three point bending beam and Eq.(10) for wedge splitting specimen [22]:

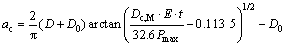 (9)

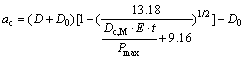            (10)

where a₀ is the initial crack length, a_c is the critical effective crack length, E is the elastic modulus of concrete, t is the thickness of the specimen, D is the depth of the specimen, and D₀ is the thickness of the knife edge for fixing the clip gauge.

3.2 Determination of CTOD_c from XU’s modified equation

Referring to the hinge model for fracture of metal materials, in which CTOD_c may be evaluated using CMOD_c (D_c,M)(see Fig.4) and a rotation factor r, XU derived the following expression to calculate the CTOD_c of concrete materials [20]:

                           (11)

where a₀ is the initial crack length, a_c is the critical effective crack length, D is the depth of the beam, and D₀ is the thickness of clip gauge holder.

Fig.3 Mechanism of FBG sensors

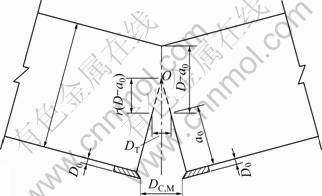
Fig.4 Relationship between CTOD_c and CMOD_c

For metal materials, the value of r is about 0.4-0.45. For concrete, XU proposed a modification for the value of r, which can be evaluated according to the following expression [20]:

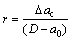                                     (12)

where Δa_c=a_c-a₀ and is determined from Eq.(9) or (10).

4 Test results and discussion

4.1 Influence of concrete strength on CTOD_c

The CTOD_c values of different strength concrete are determined by three measurement methods, i.e., FBG sensors, strain gauges, clip gauges, and two analytical methods, i.e., JENQ and SHAH’s equation, XU’s modified equation, as mentioned above. When the crack forms underneath the strain gauge, the value of CTOD_c can be obtained by multiplying the output of strain by the length of gauge. Such a conversion method was also applied by ROBINS et al [11], who investigated the crack width profile over the depth of some steel fiber reinforced concrete beams and concluded that once the crack formed under the strain gauge all the deformation recorded by the strain gauge reflected the crack opening rather than the tensile strain of the concrete. Since the values of CTOD_c are very small and usually far less than 0.1 mm, when the CTOD_c is measured, strain gauges hardly have broken. The conclusion is also applicable for the bare FBG sensor. In the current test, no tension facture failure of strain gauges and FBGs attached at the crack tip of specimen was observed when the peak load was reached. Therefore, the CTOD_c was calculated based on the above mentioned conversion method. Attention should be paid to the fact that the value of CTOD_c should be treated invalid if the debonding of the strain gauge or FBG sensor was observed in the test or if the crack of concrete did not go through the gauge length or the grating of the FBG.

The average values of CTOD_c measured from FBG sensors, strain gauges, clip gauges and the predicted ones based on Eq.(8) and Eq.(11) are summarized in Table 2 for each group of specimens (6 identical specimens).

For TPB specimens with concrete strength varying from 30 MPa to 150 MPa, the CTOD_c measured by FBG sensors and strain gauges exhibit the similar average value of about 30 μm, which is well predicted by XU’s equation [20] (see Fig.5(a)). Comparatively, the CTOD_c measured by clip gauges shows a higher average value of about 40 μm, which is similar to that predicted by JENQ and SHAH’s equation [19]. The values measured from the clip gauges show a quite large variation (27.0-38.4 μm). The possible reason is that the CTOD_c measured by the clip gauge is sensitive to the location of the knife edge attached around the crack tip. There is no clear dependence of CTOD_c on concrete strength within the testing range. The main reason might be that the maximum size of coarse aggregates is the same for all seven types of concrete.

Table 2 Summary of test results

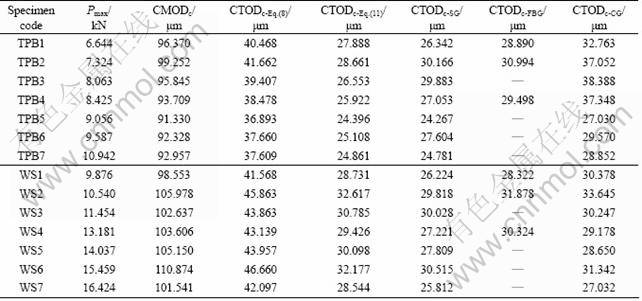
For WS specimens, the CTOD_c measured by three different methods show almost the same average value of about 30 μm. There is no clear dependence of CTOD_c on concrete strength either. Similarly, XU’s modified equation [20] provides a good prediction of the CTOD_c as compared with the test results while JENQ and SHAH’s equation [19] generally leads to an overestimation. There is a general tendency that the CTOD_c measured from the strain gauges is slightly smaller than that measured from FBG sensors in both TPB and WS specimens. It is considered that the results from FBG sensors are more close to the reality since their diameter is only about 125 μm and could be attached very closely to the crack tip as compared with strain gauges, of which the center-line has a larger distance (2.0 mm in the current study) from the crack tip (see Fig.2(c)) because of their relatively large bonding surface.

4.2 Geometry effect on CTOD_c

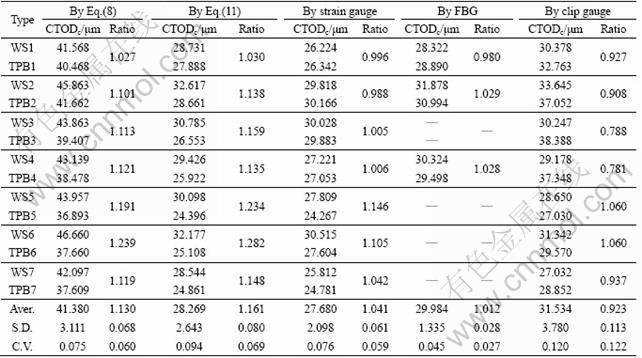
Figures 5(a) and 5(b) present the values of CTOD_c in TPB and WS specimens, respectively. No noticeable difference in CTOD_c is found between the two types of test geometries. Table 3 presents the ratio of CTOD_c measured in WS specimens to that measured in TPB specimens. The average values of such a ratio based upon Eq.(8) and Eq.(11) are 1.113 and 1.161, respectively. On the other hand, the experimental values of the ratio are 1.041, 1.012 and 0.923, respectively, when strain gauges, FBG sensors and clip gauges are applied for the measurement of CTOD_c. On the whole, it can be said that no obvious geometry effect on CTOD_c is observed.

Fig.5 Measured and calculated CTOD_c of different strength concretes: (a) TPB specimens; (b) WS specimens

Table 3 Geometry effect on CTOD_c

5 Conclusions

1) The CTOD_c has no clear dependence on the concrete strength within the testing range from 30 MPa to 150 MPa.

2) JENQ and SHAH’s equation generally leads to an overestimation of the CTOD_c of concrete, while XU’s modified equation provides a satisfactory prediction as compared with the experimental results.

3) The FBG sensors method is able to provide a more accurate measurement of CTOD_c of concrete as compared with the use of strain gauges and clip gauges because of their much smaller diameter which enables them to be arranged as closely as possible to the crack tip.

4) The CTOD_c of concrete with different strength grades seems to be independent of the specimen geometry.

References

[1] JENQ Y S, SHAH S P. A fracture-toughness criterion for concrete [J]. Engineering Fracture Mechanics, 1985, 21(5): 1055-1069.

[2] ZHOU F P, BARR B I G, LYDON F D. Fracture properties of high-strength concrete with varying silica fume content and aggregates [J]. Cement and Concrete Research, 1995, 25(3): 543-552.

[3] XIAO J Z, SCHNEIDER H, D?NNECKE C, K?NIG G. Wedge splitting test on fracture behaviour of ultra high strength concrete [J]. Construction and Building Materials, 2004, 18(6): 359-365.

[4] LIN Chen, JIN Xian-yu, LI Zong-jin. Experimental study on some factors affecting fracture property of concrete [J]. China Concrete and Cement Products, 2004, 5: 7-9. (in Chinese)

[5] BARR B I G, ABUSIAF H F, SENER S. Size effect and fracture energy studies using compact compression specimens [J]. Materials and Structures, 1998, 31(205): 36-41.

[6] NAVALURKAR R K, HSU C T T, KIM S K, WECHARATANA M. True fracture energy of concrete [J]. ACI Materials Journal, 1999, 96(2): 213-225.

[7] ZHAO Zhi-fang, XU Shi-lang. Influence of compressive strength of concrete upon new K_R-curve based on the cohesive force [J]. Journal of Hydroelectric Engineering, 2001, 74: 11-21. (in Chinese)

[8] ANSARI F. Stress-strain response of microcracked concrete in direct tension [J]. ACI Materials Journal, 1987, 84(6): 481-490.

[9] ANSARI F. Mechanism of microcrack formation in concrete [J]. ACI Materials Journal, 1989, 86(5): 459-464.

[10] XU Shi-lang, REINHARDT H W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part I: Experimental investigation of crack propagation [J]. International Journal of Fracture, 1999, 98(2): 111-149.

[11] ROBINS P, AUSTIN S, CHANDLER J, JONES P. Flexural strain and crack width measurement of steel-fibre-reinforced concrete by optical grid and electrical gauge methods [J]. Cement and Concrete Research, 2001, 31(5): 719-729.

[12] ANSARI F, NAVALURKAR R. Kinetics of crack formation in cementitious composites by fiber optics [J]. Journal of Engineering Mechanic, 1993, 119(5): 1048-1061.

[13] CHEN X, ANSARI F, DING H. Embedded fiber optic displacement sensor for concrete elements [C]// Proceedings of Engineering Mechanics. Fort Lauderdale: FL1-2, ACSE-EMD Special Publish, 1996: 359-365.

[14] LEE I, LIBO Y, ANSARI F, DING H. Fiber optics crack tip opening displacement sensor for concrete [J]. Cement and Concrete Composites, 1997, 19(1): 59-68.

[15] YUAN L, ANSARI F. Embedded white light interferometer fibre optics strain sensor for monitoring crack-tip opening in concrete beams [J]. Measurement Science and Technology, 1998, 9: 261-266.

[16] LEUNG C K Y, ELVIN N, OLSON N, MORSE T F, HE Y F. A novel distributed optical crack sensor for concrete structures [J]. Engineering Fracture Mechanics, 2000, 65(2/3): 133-148.

[17] LI Q B, LI G, WANG G L, YUAN L B. CTOD measurement for cracks in concrete by fiber optic sensors [J]. Optics and Lasers in Engineering, 2004, 42(4): 377-388.

[18] ZHANG Z J, ANSARI F. Crack tip opening displacement in micro-cracked concrete by an embedded optical fiber sensor [J]. Engineering Fracture Mechanics, 2005, 72(16): 2505-2518.

[19] JENQ Y S, SHAH S P. Two parameter fracture model for concrete [J]. Journal of Engineering Mechanics, 1985, 111(10): 1227-1241.

[20] XU Shi-lang. Fracture mechanisms of concrete [D]. Dalian: Dalian University of Technology, 1988.

[21] MAJUMDER M, GANGOPADHYAY T K, CHAKRABORTY A K, DASGUPTA K, BHATTACHARYA D K. Fibre Bragg gratings in structural health monitoring—Present status and applications [J]. Sensors and Actuators A, 2008, 147: 150-164.

[22] DT/T 5332—2005. Norm for fracture test of hydraulic concrete [S].

(Edited by YANG Bing)

Foundation item: Project(50438010) supported by the Key Program of the National Natural Science Foundation of China; Project(JGZXJJ2006-13) supported by the Research and Application Programs of Key Technologies for Major Constructions in the South-North Water Transfer Project Construction in China

Received date: 2010-07-29; Accepted date: 2010-11-29

Corresponding author: XU Shi-lang, Professor, PhD; Tel: +86-571-88208676; E-mail: slxu@zju.edu.cn