双线高速铁路桥最优风障高度及作用机理的数值研究

项超群¹，郭文华^{1, 2}，张佳文¹

(1. 中南大学 土木工程学院，湖南 长沙，410004；

2. 中南大学 高速铁路建造技术国家工程实验室，湖南 长沙，410004)

摘要：基于计算流体动力学理论，采用数值模拟的方法计算设置有不同高度风障的双线简支箱梁桥上高速列车的气动力，分析绕列车几何中心、迎风侧轮轨接触轴线和背风侧轮轨接触轴线的侧倾力矩，提出控制侧倾力矩和累计控制侧倾力矩的概念，并以此为依据通过不断逼近的方法得到最优的风障高度，最后对风障改善列车气动性能的机理进行研究。研究结果表明：风障的高度对列车的气动力影响较大，但根据各分力得出的最优风障高度不一致；侧倾力矩对轮轨接触轴线比几何中心大，且对风障高度也更加敏感；控制侧倾力矩当风障高度较小时为对背风侧轮轨接触轴线之矩，当风障增加到一定高度后，将转移到迎风侧轮轨接触轴线，从而对于双线桥最优风障高度并不是对背风侧或迎风侧轮轨接触轴线侧倾力矩为0 N·m的风障高度；综合考虑列车位于两线路上的气动作用，根据累计控制侧倾力矩得出气动缩尺模型的最优风障高度为95 mm，从而可知双线高速铁路简支箱梁桥上1.9 m风障效果最好。

关键词：铁路桥梁；高速列车；风障；气动力；最优高度

中图分类号：U24          文献标志码：A         文章编号：1672-7207(2014)08-2891-08

Numerical study on optimal height of wind barriers and mechanism on high-speed railway bridge with double lines

XIANG Chaoqun¹, GUO Wenhua^{1, 2}, ZHANG Jiawen¹

(1. School of Civil Engineering, Central South University, Changsha 410004, China;

2. National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410004, China)

Abstract: Based on the theory of computational fluid dynamics, the aerodynamic forces of high-speed train on simply supported box-girder bridge installed with wind barriers of various height were computed by numerical simulation. The rolling moment to the geometric center of train, windward axis of wheel-rail contact and leeward axis of wheel-rail contact were analyzed. The concepts of control rolling moment and summed control rolling moment were proposed, and the optimal height of wind barriers was found according to the concepts through approximation method. The mechanism of the improvement of wind barriers to aerodynamic performance of train was studied. The results show that the height of wind barriers has significant effect on the aerodynamic forces of train, and the optimal height is different according to different components. The rolling moment to wheel-rail contact axis is larger than that to geometric center, and is more sensitive to wind barriers height. The control rolling moment is to leeward axis of wheel-rail contact when the wind barriers is low, and it will transfer to windward axis of wheel-rail contact when the height of wind barriers increases to some value, and furthermore, the optimal height of wind barriers isn’t the height that caused the rolling moment to windward or leeward axis of wheel-rail contact to 0 N·m for double lines bridge. In consideration of aerodynamic forces of train on both lines, the optimal height of wind barriers of aerodynamic scale model is 95 mm according to summed control rolling moment. It is known that the optimal height of wind barriers is 1.9 m on high-speed railway of simply supported box-girder bridge with double lines.

Key words: railway bridge; high-speed train; wind barrier; aerodynamic forces; optimal height

为满足安全、高效、可靠的交通运输体系的需要，我国高速铁路建设得到了飞速发展。随着桥梁技术的发展和高速铁路对沉降的严格控制，铁路桥梁在全部线路中所占比例越来越大。京沪高速铁路中桥梁长度占线路总长的80.7%，全线简支梁桥总长度为956 km，占桥梁总长的90%，最常用的跨度32 m双线整孔简支梁共计27 973孔^[1]。我国地域辽阔，东南沿海地区是台风多发区，桥上线路相对较高，有些位置处于风口地段，更易受强风的影响，从而将严重影响桥上高速列车运行的安全性、舒适性。列车气动力主要由侧风下列车周围的流场分布决定，随着列车运行速度的大幅提高，很多在普通列车低速运行中被忽略的问题变得不可忽视^[2-3]。由于轻质高强材料的广泛采用，高速列车质量减轻，速度越来越快，由强侧风产生的气动力对高速列车的运行安全有着显著的影响，横向力、升力和侧倾力矩是造成整列车被吹翻、脱轨等重大意外交通运输事故的主要原因和直接原因^[4]。在铁路桥梁上设置风障后可有效改善高速列车在侧风作用下的行车稳定性，显著提高列车的临界车速^[5]，因此准确地分析风障高度和列车所受气动力的关系，既经济又安全的进行风障设置就成为一个十分重要的问题。

对于以前的铁路，已有的研究多针对路基上的列车气动性能进行分析。姜翠香等^[6]采用二维数值模型，定义车体合力对下游一侧轨顶之矩为侧滚力矩，假定一线和二线上车辆受到的侧滚力矩绝对值之和最小时的挡风墙高度为合理高度，对列车位于路基上时挡风墙合理高度和设置位置的关系进行了数值研究。高广军等^[7]取单线路堤上轨道中心线处为倾覆力矩作用点，由于车体的倾覆主要是由倾覆力矩引起，故定义倾覆力矩为0 N·m的高度为挡风墙合理高度，基于此定义采用二维模型对挡风墙合理高度进行了研究。唐煜^[8]对考虑挡风屏形式的车桥系统在横向风作用下进行二维流场分析，根据侧力系数和倾覆力矩系数得出了挡风屏的最大有效高度。在数值模拟分析时采用三维分析模型，能更精确地模拟列车沿长度方向的变化等空间效应。杨斌等^[9]采用三维模型，对平地上挡风墙距一线中心线的合理距离以及不同路况下挡风墙的合理高度进行了研究，指出不同路况下挡风墙合理高度不同。为了精确地分析高速列车的气动性能，应该考虑运行环境的影响，Bocciolone等^[10-11]研究了列车位于路堤和桥梁上时气动力的差异，Schober等^[12]测试了ICE3列车在3种不同路况下的气动力系数，指出气动力系数与路况有关。当列车在桥梁上运行时，线路一般相对较高，主梁截面亦将影响列车的外部流场，使其具有与路基上不同的气动特性，亦曾出现过大风将列车吹翻坠桥的事故^[13]，故应考虑车辆与主梁截面的相互气动影响，才能精确模拟侧风对桥上列车的空气动力作用^[14]。桥梁上的非结构性建筑如声屏障等将对列车的气动特性产生影响，罗建斌等^[15]展开了声屏障高度对列车空气动力特性的数值研究。在此，本文作者基于计算流体动力学基本理论,以大型流体工程仿真软件FLUENT为平台，研究不同风障高度下双线简支箱梁桥迎风侧线路和背风侧线路上高速列车的气动力，对不同轴线的侧倾力矩进行分析，根据对列车最不利的情况得出控制侧倾力矩，最后定义累计控制侧倾力矩的概念，得出最优的风障高度并对风障改善列车气动性能的机理进行研究。

1  计算模型及相关参数设置

1.1  几何模型

高速铁路桥梁中，使用最广泛的是简支箱梁，研究中桥梁几何模型采用京沪高速铁路中32 m双线简支箱梁桥，并对桥面轨道板等细部构造进行了简化。桥墩采用10 m高的圆端形空心墩，忽略桥墩横截面尺寸沿墩高的变化。风障采用不透风的扁平板结构，设置有风障的简支梁桥横截面见图1(a)。由于高速列车头车、尾车具有流畅线型，且其直接迎着或拖拽气体的流动，因此具有不同于中车的气动力特性。当气流流过车头一定距离后，绕流边界层的结构已趋于稳定，车辆气动力变化也趋于稳定^[15]，为节省计算机资源和计算时间，又尽可能真实地全面反映列车在流场中的气动特征，将其简化为“头车＋中车＋尾车”形式的三节车模型，同时将高速列车表面简化为一个光滑的表面，忽略转向架等的影响。采用的高速列车底面距轨道板0.2 m，其均匀段横截面尺寸如图 1(b)所示。研究中采用三维模型计算，列车处于迎风侧的高速列车-桥梁-风障气动系统三维模型见图2。对于双线简支箱梁桥，当列车处于不同线路时，气动力不同，且对不同的轴线气动力矩也存在差异，研究中对迎风侧和背风侧线路以及轮轨接触轴线的定义如图3所示。

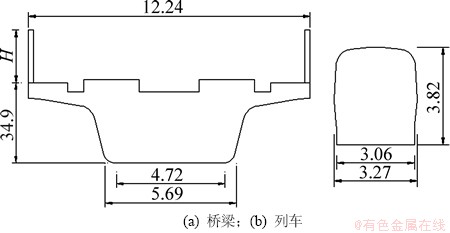
图1  横截面尺寸(单位：m)

Fig. 1  Cross section size

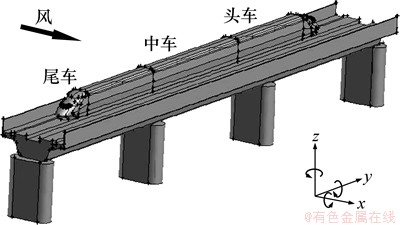
图2  高速列车-桥梁-风障系统气动力计算模型

Fig. 2  Computational model of high-speed train-bridge-wind barriers system for aerodynamic force

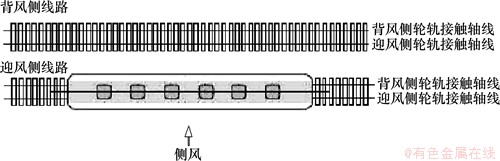
图3  迎风侧和背风侧线路及轮轨接触轴线

Fig. 3  Windward/leeward lines and axes of wheel-rail contact

1.2  计算域及网格划分

本文的风洞试验在中南大学高速铁路建造技术国家工程实验室风洞实验室进行，为了方便与风洞试验结果进行对比，车桥系统的几何缩尺比取1:20。计算域横截面按照风洞实验室低速试验段尺寸确定(宽12.0 m，高3.5 m)，由于尾流长度对数值计算结果的精确性具有重要影响，研究中采用多个长度进行试算，确定数值模型采用风洞实际长度(18.0 m)即可取得稳定的解。由于高速列车-桥梁-风障系统几何形状比较复杂，故采用非结构化的四面体网格对流场进行划分。网格越密，计算结果越接近真实值，但同时也耗费更多的计算机资源，为兼顾二者，研究中采用多重加密，在列车周围、尤其在列车车头和车尾附近划分较密的网格，逐步过渡到远离列车区域相对较稀疏的网格。将生成的网格导入FLUENT后，利用基于偏斜的光滑和交换技术重新调整网格内部节点的位置以降低网格的最大斜率，提高数值网格的质量，保证解的收敛性。

1.3  边界条件及计算参数设置

考虑风洞试验在均匀流场中进行，故数值模型中入口和出口的湍流强度均取0.5%^[16]。在入口截面处，采用横桥向风速为15 m/s、顺桥向和竖向风速为0 m/s的速度入口边界条件。在出口截面处，采用静压为0 Pa的压力出口边界条件。黏性流体在固定边界上应满足无滑移边界条件^[6]，故将高速列车、桥梁和风障表面、风洞壁面设为无滑移壁面边界条件。横风马赫数小于0.3，计算时按不可压缩定常流动问题处理^[17]。压强和速度均需要采用亚松弛迭代，计算中松弛因子应尽可能大，以加快收敛，但过大的松弛因子可能引起计算过程不稳定，求解出现发散，而太小的松弛因子则会导致收敛速度过慢，由于SIMPLE算法稳定性好，可选取较大的松弛因子，故压强速度关联算法采用SIMPLE算法。湍流模型采用RNG k-ε模型^[18]，该模型通过对湍流黏度进行修正，能更好地考虑流线弯曲程度较大的流动问题。选用基于压力的隐式求解方法计算，当监控指标升力曲线、侧力曲线和侧倾力矩曲线平稳且残差达到收敛精度(1.0×10^-4)时，认为计算收敛，迭代结束。

2  计算结果及分析

2.1  风障对列车气动力的影响

通过建立具有不同风障高度H(0.025，0.050，0.075，0.100，0.125，0.150 m)的高速列车-桥梁-风障气动缩尺模型，计算头车、中车和尾车的侧力、阻力和升力(见图4)，为了对比风障对列车气动力的遮挡效果，同时计算了不设置风障(H=0 m)的情况。研究中，桥梁采用双线简支箱梁，故分别计算了高速列车位于桥梁迎风侧线路和背风侧线路上的气动力，其方向跟总体坐标系一致(见图2)，遵循右手螺旋定则。分析可知：(1) 设置风障能显著改变列车的气动力。当风障增加到某一高度时阻力得到了有效减小且之后基本不再随风障高度变化。随风障高度的增加，侧力和升力均由正变负，因此存在最优的风障高度，使列车受到的气动作用最小。(2) 列车处于不同线路时，其气动力随风障的变化规律不同。列车处于迎风侧线路时的侧力曲线高于背风侧，但当风障高度超过125 mm后差异变小。风障高度小于100 mm时，迎风侧线路上列车阻力较大，之后两线路上阻力基本相等。当风障高度小于100 mm时迎风侧线路上升力曲线较为平缓，之后曲线变陡，而背风侧的升力曲线近似线性变化。(3) 风障的作用应使列车受到的气动力尽可能小，但从图4可知：用高速列车受到的气动力作选择风障高度的依据时，各分力得出的最优风障高度不一致，且当列车处于迎风侧线路或背风侧线路上时最优高度亦不同。

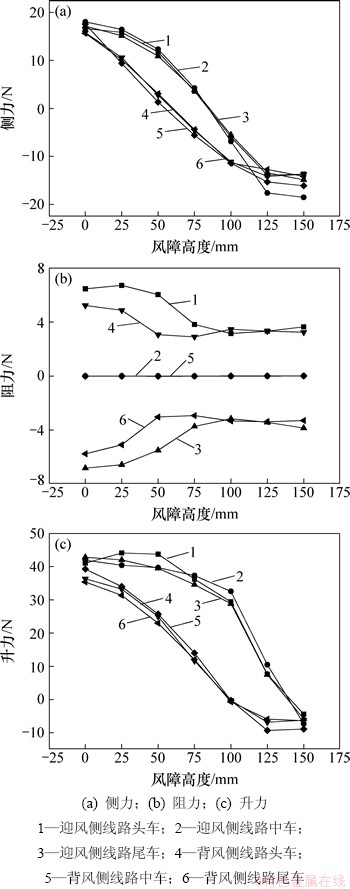
图4  高速列车气动力随风障高度的变化曲线

Fig. 4  Changing curve of aerodynamic force of high-speed train with height of wind barriers

2.2  风障对列车侧倾力矩的影响

高速列车在强侧风下发生倾覆，主要是高速列车的侧力、升力和二者共同产生的侧倾力矩过大造成的，其中侧倾力矩是衡量列车横风稳定性最重要的指   标^[4]。通过计算可知，高速列车的侧力和升力在不同高度风障下可能与不设置风障时方向相反，因此列车受到侧风后可能绕迎风侧轨道侧翻，也可能绕背风侧轨道侧翻，如图5所示，研究中先对列车几何中心提取侧倾力矩M_y，然后将力矩作用点转移到轮轨接触轴线上，可表示为：

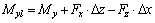         (1)

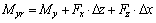         (2)

式中：F_x·Δz和F_z·Δx分别为侧力和升力对轮轨接触轴线产生的矩。

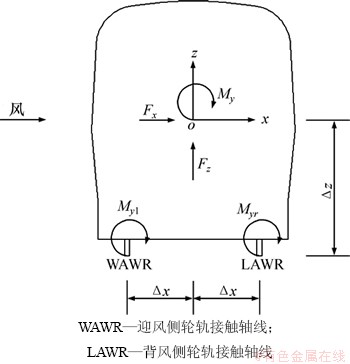
图5  侧倾力矩作用示意图

Fig. 5  Diagram of rolling moment

侧倾力矩随风障高度的变化曲线如图6所示。由图6可知：(1) 头车、中车和尾车对几何中心的力矩都较小，将力矩作用转移到轮轨接触轴线后，侧倾力矩大幅增加，且其对风障高度变化也更加敏感。(2) 设置风障后，三节车对背风侧轮轨接触轴线的侧倾力矩得到了有效减小，且当风障达到某一高度后侧倾力矩将改变方向。不设置风障时对迎风侧轮轨接触轴线的侧倾力矩很小，设置风障后对该轴线的力矩反而增大。(3) 高速列车位于不同线路上时，对迎风侧轮轨接触轴线的侧倾力矩较接近，但对背风侧轮轨接触轴线则有较大差异。

2.3  高速列车的控制侧倾力矩

计算可知，高速列车侧倾力矩可能对迎风侧轮轨接触轴线较大，也可能对背风侧轮轨接触轴线较大。在图5中，当M_yr为正时，列车有顺时针方向侧倾的趋势，当M_yl为负时，列车有逆时针方向侧倾的趋势，且二者绝对值较大者起控制作用，而当M_yr为负或M_yl为正时，均能提高列车侧风下的稳定性，根据最不利情况定义控制侧倾力矩M_ycon：

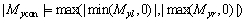   (3)

其正负跟绝对值较大者保持一致。

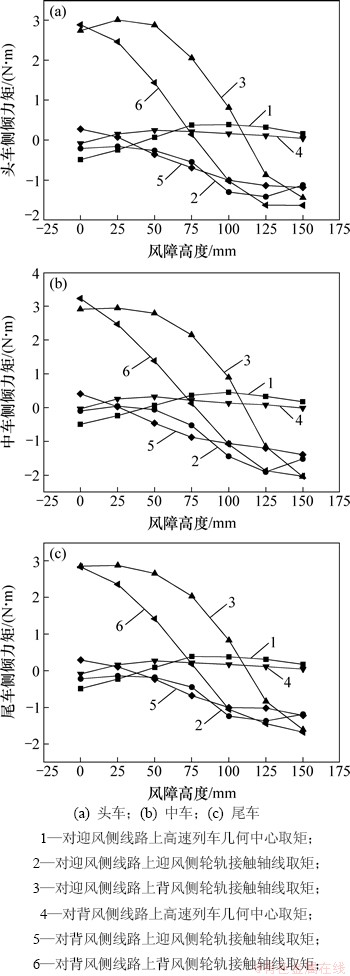
图6  侧倾力矩随风障高度的变化曲线

Fig. 6  Changing curves of rolling moment with height of wind barriers

不同风障高度下高速列车位于2条线路上的控制侧倾力矩随风障高度的变化曲线如图7所示。由图7可知：(1) 对于迎风侧线路当风障高度小于75 mm、背风侧线路小于50 mm时，控制侧倾力矩均为正值，即列车受到绕背风侧轮轨接触轴线的侧倾力矩较大，之后控制侧倾力矩变为负值，即控制侧倾力矩从背风侧轴线转移到迎风侧轴线。(2) 高速列车位于迎风侧线路上时在风障高度75~100 mm内，位于背风侧线路上时在风障高度50~75 mm内，可分别得到控制侧倾力矩最小的风障高度，但针对不同线路得到的高度不同，且三节车略有差异。

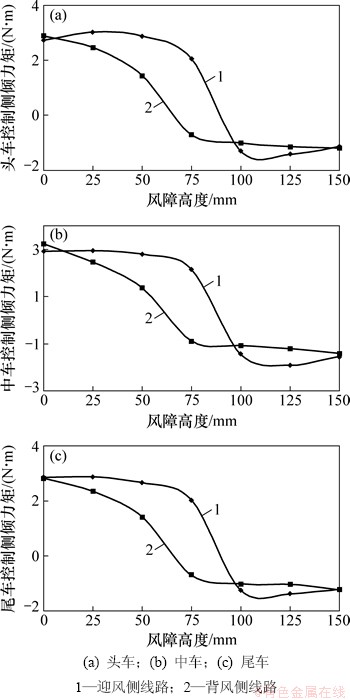
图7  控制侧倾力矩随风障高度的变化曲线

Fig. 7  Changing curve of control rolling moment with height of wind barriers

2.4  最优风障高度的选取

当列车处于迎风侧线路或背风侧线路时，均能得到控制侧倾力矩最小的风障高度，但2条线路上得出的高度不同，为了统一考虑列车位于不同线路上时控制侧倾力矩的作用，将控制侧倾力矩进行分段线性插值，并取绝对值之和为累计控制侧倾力矩M_sum，即：

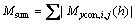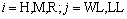()  (4)

式中，H，M，R分别代表头车、中车、尾车；WL和LL分别代表迎风侧线路和背风侧线路。

累计控制侧倾力矩M_sum曲线如图8所示。由图8可知，当风障高度为90 mm时，M_sum取得最小值，即可初步认为气动缩尺模型中90 mm为最优风障高度。

由于累计控制侧倾力矩M_sum是基于分段线性的假定得出的，但控制侧倾力矩在每段并不一定严格按线性变化，因此初步得出最优风障高度后仍需按其建立气动缩尺模型进行复核，更新累计控制侧倾力矩曲线并得出更新后的最优风障高度，研究中认为更新后的最优高度与原最优高度相对误差不大于3%即取得真值。通过2次迭代复算，得出气动缩尺模型的最优风障高度为95 mm，通过缩尺比换算可知工程中1.9 m为高速铁路双线简支箱梁桥的最优风障高度。

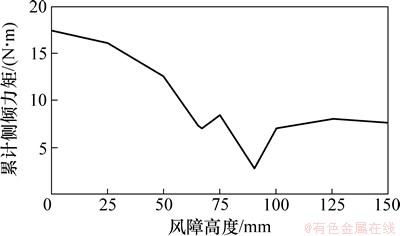
图8  累计控制侧倾力矩随风障高度的变化曲线

Fig. 8  Changing curve of summed control rolling moment with height of wind barriers

最优风障高度下中车侧倾力矩如图9所示。从图9可见：对于迎风侧线路，当对迎风侧轮轨接触轴线的侧倾力矩为0 N·m时，对背风侧轴线的侧倾力矩与不设置风障时基本相等，对背风侧轮轨接触轴线的侧倾力矩为0 N·m时，对迎风侧轴线的力矩已大幅增加，此时控制侧倾力矩已转移到迎风侧轮轨接触轴线。从而可知：对于双线简支箱梁桥，最优高度并不是对背风侧轮轨接触轴线或迎风侧轮轨接触轴线侧倾力矩为0 N·m的风障高度，同理也不能只考虑列车位于迎风侧线路或背风侧线路的情况。

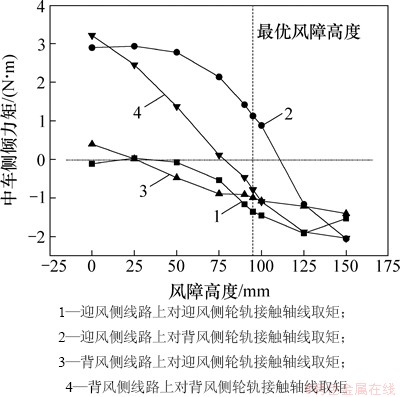
图9  最优风障高度下中车侧倾力矩

Fig. 9  Rolling moment of middle train under wind barriers of optimal height

2.5  流场特性分析

为了研究最优高度风障挡风作用的机理，取中车纵向对称截面，分析当列车处于迎风侧线路上时其速度矢量分布和静压分布等流场特性与不设置风障时的差异。

速度矢量分布如图10所示。由图10可知：

(1) 风障的设置改变了气流的流动。不设置风障时，气流抵达列车迎风侧后沿着流线型车身向上运动，在车顶背风侧角点处呈俯角脱离车身，车身背风侧附近气流向下运动。设置风障后，气流流过风障抵达车身迎风侧靠上部位，之后有部分气流沿着车身向下运动，而紧靠车身背风侧气流则向上运动。

(2) 风障的设置改变了风速的分布。不设置风障时，流场中列车迎风侧顶角处风速最大，接近于入口风速的2倍。设置风障后，列车迎风侧顶角处风速比不设风障时略小。风障的设置主要改变了风障与列车之间的气流速度，对外围的风速影响不大。

(3) 风障的设置改变了漩涡的分布。不设置风障时，在列车迎风侧外侧贴近桥面处有一较小的顺时针方向的漩涡，背风侧线路上有较大的逆时针方向的漩涡。设置风障后，在迎风侧风障和列车之间有较大的顺时针方向的漩涡，由于风障的作用，从迎风侧穿过列车底部的气流大幅减少，背风侧线路上气流运动方向与来流反向，且无漩涡产生。

静压分布云图如图11所示。由图11可知：

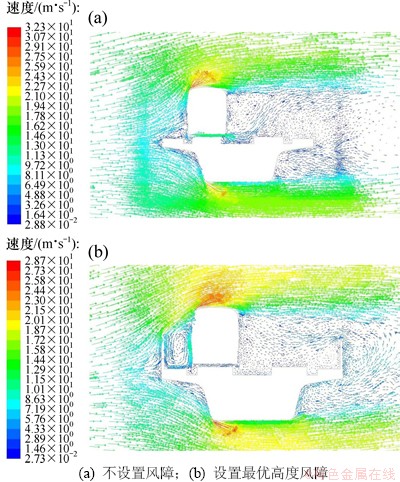
图10  速度矢量分布

Fig. 10  Distribution of velocity vector

图11  静压分布云图(单位：Pa)

Fig. 11  Contour of static pressure distribution

(1) 不设置风障时，列车迎风侧正压较大，同时其背风侧为负压，故将迎风侧正压和背风侧负压对列车侧面的面积分叠加得到的侧力较大。设置风障后，车辆迎风侧和背风侧均为负压，且大小相近，因此列车车身两侧受到的侧力作用基本抵消。

(2) 在横风作用下，车辆受到的气动升力主要是车体顶部和底部压力分布差异造成的，设置风障后，车顶负压减小，从而列车受到的升力得到了减小。

(3) 不设置风障时，列车迎风侧正压越靠近桥面数值越大，其合力对车辆几何中心的力矩绕逆时针方向，车顶负压最大值出现在迎风一侧，对几何中心的力矩为顺时针方向，故二者相互抵消，从而对列车几何中心的侧倾力矩较小。迎风侧正压和车顶负压对背风侧轮轨接触轴线的力矩方向相同，因此对该轴的侧倾力矩较大。设置风障后，列车迎风侧为负压，其对两轮轨接触轴线的矩均为逆时针方向，车顶负压且靠近迎风侧数值较大，因此其对背风侧轴线为顺时针方向的力矩，故侧力力矩和升力力矩对该轴线相互抵消，而升力力矩对迎风侧轴线的力臂较小，所以对迎风侧轴线的力矩作用也不大。

3  结论

(1) 设置风障能有效改变列车的气动力。根据高速列车受到的气动力选择风障高度时，各分力得出的最优风障高度不统一，且当列车处于迎风侧线路或背风侧线路上时最优高度不同。

(2) 头车、中车和尾车对几何中心的侧倾力矩都较小。由于侧力和升力的共同作用，对轮轨接触轴线的力矩比几何中心大，且其对风障高度变化也更敏感。

(3) 高速列车侧倾力矩可能对迎风侧轮轨接触轴线较大，也有可能对背风侧轮轨接触轴线较大，且只有当侧倾力矩对列车产生偏离平衡位置的作用时才不利于强横风下列车的稳定性，据此定义了控制侧倾力矩的概念。

(4) 为了统一考虑列车位于双线简支箱梁桥迎风侧线路和背风侧线路的情况，定义了累计控制侧倾力矩，并采用逐步逼近的方法得出了缩尺模型的最优高度为95 mm，从而可知实桥中1.9 m为最优风障高度。对最优风障高度下列车的侧倾力矩进行分析，指出选取风障高度时若只根据对一侧轮轨接触轴线力矩最小的原则可能得出不合理的结论。

(5) 风障的设置有效改变了列车车身周围气流的流动方式、气流速度、漩涡的分布以及静压分布等，因此风障能有效改善强侧风作用下运行于桥梁上的高速列车气动性能。

参考文献：

[1] 孙树礼. 京沪高速铁路桥梁工程[J]. 铁道标准设计, 2008(6): 1-4.

SUN Shuli. Bridge engineering in the Beijing-Shanghai high-speed railway[J]. Railway Standard Design, 2008(6): 1-4.

[2] Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38(6/7): 469-514.

[3] 田红旗. 中国列车空气动力学研究进展[J]. 交通运输工程学报, 2006, 6(1): 1-9.

TIAN Hongqi. Study evolvement of train aerodynamics in china[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 1-9.

[4] 刘凤华. 不同类型挡风墙对列车运行安全防护效果的影响[J]. 中南大学学报(自然科学版), 2006, 37(1): 176-182.

LIU Fenghua. Wind-proof effect of different kinds of wind-break walls on the security of trains[J]. Journal of Central South University (Science and Technology), 2006, 37(1): 176-182.

[5] 陈涛. 高速铁路桥梁风障设置对列车及主梁气动性能影响研究[D]. 长沙: 中南大学土木工程学院, 2011: 3-20.

CHEN Tao. The study on the impact of the setting of high-speed railway bridge’s wind barrier on the train and main beam’s aerodynamic performance[D]. Changsha: Central South University. School of Civil Engineering, 2011: 3-20.

[6] 姜翠香, 梁习锋. 挡风墙高度和设置位置对车辆气动性能的影响[J]. 中国铁道科学, 2006, 27(2): 66-70.

JIANG Cuixiang, LIANG Xifeng. Effect of the vehicle aerodynamic performance caused by the height and position of wind break wall[J]. China Railway Science, 2006, 27(2): 66-70.

[7] 高广军, 段丽丽. 单线路堤上挡风墙高度研究[J]. 中南大学学报(自然科学版), 2011, 42(1): 254-259.

GAO Guangjun, DUAN Lili. Height of wind barrier on embankment of single railway line[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 254-259.

[8] 唐煜. 桥梁挡风屏对强侧风条件下列车运营安全性的影响[D]. 成都: 西南交通大学土木工程学院, 2010: 8-16.

TANG Yu. The bridge-windbreak influence on the operational safety of vehicle under crosswind[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2011: 8-16.

[9] 杨斌, 刘堂红, 杨明智. 大风区铁路挡风墙合理设置[J]. 铁道科学与工程学报, 2011, 8(3): 67-72.

YANG Bin, LIU Tanghong, YANG Mingzhi. Reasonable setting of wind break wall on railway in strong wind areas[J]. Journal of Railway Science and Engineering, 2011, 8(3): 67-72.

[10] Bocciolone M, Cheli F, Corradi R, et al. Crosswind action on rail vehicles: wind tunnel experimental analyses[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 584-610.

[11] Cheli F, Corradi R, Rocchi D, et al. Wind tunnel tests on train scale models to investigate the effect of infrastructure scenario[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98: 353-362.

[12] Schober M, Weise M, Orellano A, et al. Wind tunnel investigation of an ICE 3 endcar on three standard ground scenarios[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98: 345-352.

[13] 刘庆宽, 杜彦良, 乔富贵. 日本列车横风和强风对策研究[J]. 铁道学报, 2008: 30(1): 82-88.

LIU Qingkuan, DU Yanliang, QIAO Fugui. Train-crosswind and strong wind countermeasure research in Japan[J]. Journal of the China Railway Society, 2008, 30(1): 82-88.

[14] 岳澄, 张伟. 车桥耦合气动力特性和风压分布数值模拟[J]. 天津大学学报, 2007, 40(1): 68-72.

YUE Cheng, ZHANG Wei. Numerical simulation for aerodynamic characteristic and wind pressure distribution of vehicle-bridge coupled system[J]. Journal of Tianjin University, 2007, 40(1): 68-72.

[15] 罗建斌, 胡爱军. 高架桥声屏障高度对列车气动特性影响的数值模拟[J]. 计算物理, 2012, 29(1): 65-72.

LUO Jianbin, HU Aijun. Numerical simulation of the effect of viaduct noise barrier height on train aerodynamic characteristics[J]. Chinese Journal of Computational Physics, 2012, 29(1): 65-72.

[16] 宋瑞斌. 高速列车通过桥梁时相互气动性能的数值研究[D]. 长沙: 中南大学土木工程学院, 2011: 6-20.

SONG Ruibin. The numerical study of aerodynamic characteristics of each other when high-speed train move on bridge[D]. Changsha: Central South University. School of Civil Engineering, 2011: 6-20.

[17] 吴建民. 高等空气动力学[M]. 北京: 北京航空航天大学出版社, 1992: 39-54, 164-174.

WU Jianmin. Advanced aerodynamics[M]. Beijing: Beihang University Press, 1992: 39-54, 164-174.

[18] 周奇, 朱乐东, 郭震山. 曲线风障对桥面风环境影响的数值模拟[J]. 武汉理工大学学报, 2010, 32(10): 38-44.

ZHOU Qi, ZHU Ledong, GUO Zhenshan. Numerical simulation for curve windshield barrier effects on wind environment around bridge deck[J]. Journal of Wuhan University of Technology, 2010, 32(10): 38-44.

(编辑  赵俊)

收稿日期：2013-07-14；修回日期：2013-10-20

基金项目：国家自然科学基金资助项目(51078356)；铁道部科技研究开发计划重大项目(2008G031-Q)

通信作者：郭文华(1969-)，男，湖南常德人，教授，博士生导师，从事桥梁结构振动与稳定、风工程研究；电话：13973160678；E-mail：whguo@126.com