J. Cent. South Univ. (2017) 24: 2853-2861

DOI: https://doi.org/10.1007/s11771-017-3700-9

A supervised multimanifold method with locality preserving for face recognition using single sample per person

Nabipour Mehrasa¹, Aghagolzadeh Ali², Motameni Homayun¹

1. Department of Computer Engineering, Faculty of Engineering, Sari Islamic Azad University,Sari, 48161-19318, Iran;

2. Faculty of Electrical and Computer Engineering, Babol Noshirvani University of Technology,Babol, 47148-71167, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017

Abstract: Although real-world experiences show that preparing one image per person is more convenient, most of the appearance-based face recognition methods degrade or fail to work if there is only a single sample per person (SSPP). In this work, we introduce a novel supervised learning method called supervised locality preserving multimanifold (SLPMM) for face recognition with SSPP. In SLPMM, two graphs: within-manifold graph and between-manifold graph are made to represent the information inside every manifold and the information among different manifolds, respectively. SLPMM simultaneously maximizes the between-manifold scatter and minimizes the within-manifold scatter which leads to discriminant space by adopting locality preserving projection (LPP) concept. Experimental results on two widely used face databases FERET and AR face database are presented to prove the efficacy of the proposed approach.

Key words: face recognition; locality preserving; manifold learning; single sample per person

1 Introduction

Appearance-based methods are one of the most successful face recognition techniques which have been developed over the past few decades. However, some of the widely used appearance-based techniques such as Eigenface [1], that suffers serious performance drop, and Fisherfaces [2] even cannot be used where only one sample image per person is available for training. This problem is called single sample per person (SSPP) problem. To address the SSPP problem, many methods have been developed [3]. These methods can be mainly divided into four categories: principal component analysis (PCA) extensions, generic learning, virtual sample generation, and image partitioning.

PCA had been extended many different versions such as, (PC)²A [4], E(PC)²A [5], 2DPCA [6] and a novel proposed method named UP [7] which can reduce the recognition errors, to deal with the SSPP problem. Unfortunately, PCA-based methods do not utilize the intra-personal variations and this affects their performance in recognition of facial images which include large variations. In the second category, besides the single sample gallery, an aiding generic training set, in which every person has more than one sample, was collected from the other subjects, for using in a training phase [8]. CAN et al [9] proposed a method which collects a generic training set per subject containing images of the other persons who are similar enough to that subject. They further presented a new method with a new nonlinear estimation of the within-class scatter matrix called Riemannian mean [10]. These methods affect the size and choice of the generic training set.

Methods in the third category generate some extra sample images for each person in the database. YIN et al [11] obtained multiple training samples from a single face image by sampling and then applied Fisher linear discriminant analysis (FLDA). ZHANG et al [12] and GAO et al [13] proposed two methods based on the singular value decomposition (SVD) to obtain several images per person. Then they applied 2D-FLDA for feature extraction. The virtual images do not contain significant features because they highly depend on prior information gained by single face image per person. In the fourth category, a face image is decomposed into a set of patches, and then the feature extraction can be applied. CHEN et al [14] employed FLDA on image patches which were obtained by partitioning every single face image. TAN et al [15] presented an unsupervised subspace learning method which uses a self-organizing map (SOM). KANAN et al [16] proposed a method that extracts an array of pseudo Zernike moments (PZM) from the local areas of every face image. These methods may be more suitable to deal with SSPP problem [3]: every single face image is represented by a set of low dimensional local feature vectors rather than one high dimensional vector.

Recently, many research results have shown that face images may reside on a nonlinear sub-manifold, such as ISOMAP [17] and LLE [18] which are two classical manifold learning techniques. LU et al [19] proposed an approach called discriminative multimanifold analysis (DMMA) which has considered the local patches of each person as a manifold and the SSPP face recognition is converted into a manifold- manifold matching problem. This method achieved interesting results in face recognition with SSPP. In Ref. [20], we have proposed a method to transform DMMA to the frequency domain. Further, we have presented an improved version of DMMA namely I-DMMA [21] in DCT domain that automatically determines the local neighborhood size. DMMA and its novel versions contain an optimization step finding the best projection matrices. Thus, the computational time of these methods is high.

HE et al [22] proposed the locality preserving projections (LPP) which are designed for preserving the local structure by minimizing the local scatter of the projected data samples. Unlike most manifold learning algorithms, the main advantage of LPP is that it can generate a linear explicit map [23], thus, LPP is fast and suitable for practical applications. Inspired by these methods and the idea of Ref. [23] which developed LPP in LDA framework, in this work, we develop a novel method, named supervised locality preserving multimanifold (SLPMM), for face recognition with SSPP. Our proposed method is a supervised graph embedding approach which preserves the intra class information based on the LPP criterion. We propose to use two graphs to achieve both intra class compactness and inter class separation at the same time. In fact, we use LPP in a discriminative multimanifold analysis framework. SLPMM is a linear supervised feature extraction method, which explicitly considers different manifolds for different people. Unlike LPP, SLPMM uses the class label information.

2 Related works

2.1 DMMA

DMMA is a recently proposed manifold learning method for face recognition with single training sample per person. This method divides every face image into multiple non-overlapping patches and considers every image patches as a manifold. So DMMA attempts to transfer the manifolds to several new spaces with a distribution that includes maximum margin between different manifolds corresponding to the different persons.

Given a training set 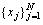whereis a training image of the jth person and N is the number of persons in the training set. First, each image x_j is divided into t non-overlapping local patches with an equal size of a×b, where 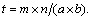Given 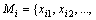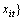is the image patch set of the ith person as a manifold M_i. The inter-manifold and intra-manifold covariance matrices can be calculated by Eqs. (1) and (2), where A_irp and B_irp are two affinity matrices for weighting the k₁-inter-manifold neighbors and k₂-intra-manifold neighbors of x_ir, respectively. 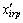represents the pth k₁-nearest inter-manifold neighbors and x_irq denotes the qth k₂-nearest intra-manifold neighbors of x_ir. The bases of the projection matrix W_i can be determined by solving eigenvalue in Eq. (3), 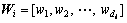is the projection matrix of the ith manifold.

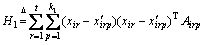            (1)

             (2)

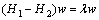                            (3)

2.2 Locality preserving projections

Locality preserving projections (LPP) is a linear dimensionality reduction method which explicitly considers the manifold structure. LPP is designed for preserving local neighborhood information. Let X=[x₁, x₂, …, x_n] denote the original data points in a high dimensional space. Given Y=[y₁, y₂, …, y_n] is the corresponding low dimensional representation. The objective function of LPP is calculated as

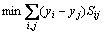                            (4)

where S is a similarity matrix that typically contains Gaussian weights by using k-nearest or ε–ball neighborhood. After some simple algebra formulation, the objective function of LPP becomes:

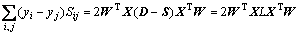(5)

where D is a diagonal matrix whose entries are column(or row, since S is symmetric) sums of S, 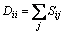,then the Laplacian matrix is given by L=D–S and S_D=XDX^T, S_L=XLX^T. Finally by imposing the constraint W^TXDX^TW=W^TS_DW=1, the objective function of LPP can be obtained as

                             (6)

The projection matrix W is given by the minimum eigenvalue solution to the following generalized eigenvalue problem as

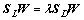                               (7)

3 Proposed approach

3.1 Motivation

Before going into the details of our proposed method, more analysis was done about DMMA and its improved version I-DMMA. We randomly selected four subjects from the FERET database (which are shown in Fig. 1) to visualize the manifold structure of the local patches. Each face image is partitioned into multiple patches. Figures 2, 3 and 4 show the plots of these samples (image patches) in two dimensional subspaces, i.e., only the first two dimensions of each patch were used.

The visualization of distribution of image patches in the original space is shown in Fig. 2. Figure 3 visualizes the embedding of faces associated with these four subjects obtained with the DMMA. As can be seen, after embedding, there is a good separation for the manifolds corresponding to different persons. Figure 4 visualizes the embedding of the same four persons obtained with the I-DMMA. Although the manifolds are better separated in the embedded space obtained by I-DMMA method, it can be seen that the local structure of every manifold is not completely preserved. So it seems that a discriminative method with the ability of preserving local information can be useful.

3.2 Supervised locality preserving multimanifold

The aim of SLPMM is to find N projection matrices to project the manifolds into low dimensional spaces, such that the points from the same manifold are close, and the points from different manifolds are far from each other. It is supposed that N face images are associated with N people in the training data set. First, we partition each image into t nonoverlapping patches. Second, all patches associated to one face image of a person were considered as points on a manifold, thus there are N manifolds. In order to discover the discriminant structure of these manifolds, we define two types of graphs: within-manifold graph G_w with t nodes and the between-manifold graph G_b with N nodes. In each of two graphs, we put an edge between two nodes, if they are nearest neighbors. We apply the conventional k-nearest neighbor method to find within-manifold and between-manifold neighbors. Let S_w and S_b be the similarity matrices of G_w and G_b, respectively. For the within-manifold graph G_w, an edge is constructed between nodes x_ir and x_il from the same manifold (ith manifold). The similarity between x_ir and x_il is defined as

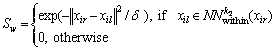  (8)

where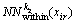denotes the k₂-within-manifold neighbors set of x_ir. If S_w denotes the symmetric affinity matrix and D_w is the diagonal weight matrix, whose entries are column (or row) sums of S_w, then the Laplacian matrix is given by L_w=D_w–S_w. The within-manifold locality preserving criterion is defined as

                        (9)

Let M=[m₁, m₂, …, m_N] denote the average set of manifolds, i.e., m_i denotes the mean vector of ith manifold. To achieve the goal of maximum margin among different manifolds, the low dimensional manifolds should be clearly separated in the embedded space. For the between-manifold graph G_b, we define the similarity matrix as

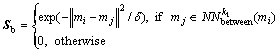 (10)

where 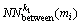denotes the k₁-between-manifold neighbors set of m_i. If S_b denotes the symmetric affinity matrix and D_b is the diagonal weight matrix, whose entries are column (or row) sums of S_b, then the Laplacian matrix is given by L_w=D_w–S_w. The between- manifold separation criterion is defined as

Fig. 1 FERET-1 sample images associated to four persons

Fig. 2 Manifolds in original space

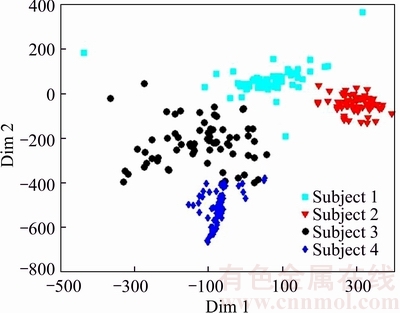
Fig. 3 Embedded faces using DMMA

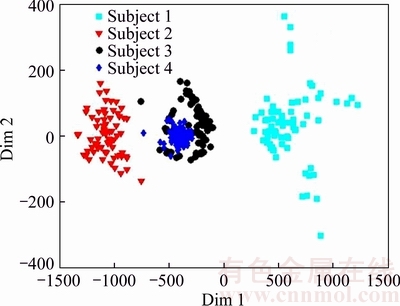
Fig. 4 Embedded faces using I-DMMA

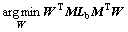                       (11)

Consequently, the objective functions are mentioned as

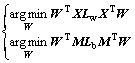                      (12)

The above two objective functions can be combined into one single objective function:

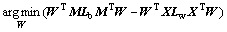        (13)

So the within-manifold Laplacian covariance and between-manifold Laplacian covariance can be written as

                              (14)

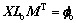                               (15)

Now, Eq. (13) can be written as

        (16)

where J denotes the multimanifold maximum margin criterion and the parameter β (0<β<1) is a nonnegative constant which balances the relative merits of maximization the between-manifold Laplacian scatter to the minimization of the within-manifold Laplacian scatter. This gives a generalized eigenvalue problem having the form defined as

                      (17)

Let the column vectors w₁, w₂, …, w_di be the generalized eigenvectors of Eq. (17) according to their eigenvalues: λ₁≥λ₂≥…≥λ_di. Then the projection matrix of W_i will be given by concatenating the obtained eigenvectors W_i=[w ₁, w ₂, …, w_di.], d_i denotes the low dimensional feature size learned by W_i . It is worth noting that (f_b–f_w) is not positive definite, i.e. the eigenvalues of (f_b–f_w) may have a positive, zero and negative value λ₁≥λ₂≥…≥λ_di≥0≥λ_di+1≥…≥λ_d. Thus based on the idea of Ref. [19], we assume that the samples are projected to eigenvectors w_j corresponding to eigenvalue λ_j, then the multimanifold maximum margin criterion becomes:

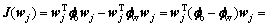
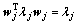               (18)

Consequently λ_i>0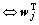f_bw_j>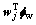w_j; obviously a good projection is done. So the projection matrix W consists of the eigenvectors corresponding to the positive eigenvalues of the eigenvalue Eq. (17). Figure 5 shows the embedded manifolds corresponding to four persons in Fig. 1 obtained with the proposed SLPMM. It is clear that the embedded manifolds are moderately better separated and the corresponding locality scatter are better preserved compared with the results given in Figs. 3 and 4.

3.3 SLPMM algorithm

Like Refs. [20] and [21], the DCT features can be used as initial feature vectors in the proposed SLPMM. By using DCT, an additional step in the SLPMM algorithm (step 2) is included. However, in the following algorithm we have mentioned the DCT step, it can be ignored and just each image patch can be transferred into the vector. For a digital image with the size of M×N,f(x,y) is the image intensity function, and its 2-dimensional DCT is defined by:

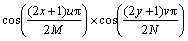
             (19)

As a result of applying DCT to an image or a block of an image, a DCT coefficient matrix with the same size is achieved. The most of the large magnitude DCT coefficients are located in the upper left part of the DCT coefficient matrix (i.e. low and middle frequencies). These coefficients contain significant information and construct the basic structure of the image. Motivated by this fact, in Refs. [20] and [21], we proposed to select the upper left part of the DCT coefficient matrix associated with each image patch, in order to extract initial DCT features. Figure 6 illustrates the selection of the lowest DCT frequency features.

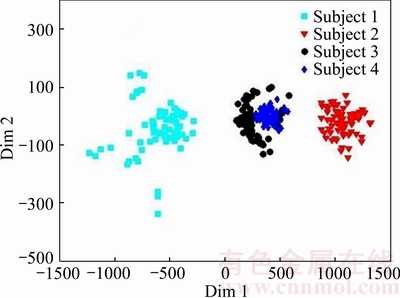
Fig. 5 Embedded faces using SLPMM

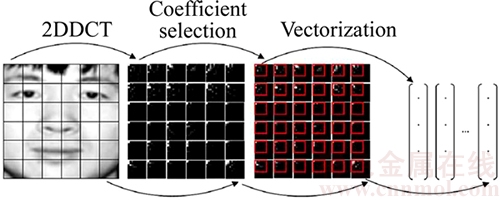
Fig. 6 DCT coefficient selection [21]

Finally, we can summarize our proposed SLPMM feature extraction algorithm as follows:

Step 1: Partition each image into several nonoverlapping patches.

Step 2: For each image patch (in DCT domain):

1) Apply 2DDCT as shown in Eq. (19);

2) Select an upper-left sub-block of DCT coefficient matrix as shown in Fig. 6;

3) Vectorize the retained DCT coefficients as DCT feature vectors.

Step 3: Find the within-manifold and between- manifold nearest neighbors.

Step 4: Construct the within-manifold graph and the between-manifold graph.

Step 5: Compute within-manifold Laplacian covariance f_w and between-manifold Laplacian covariance f_b as shown in Eqs. (14) and (15), respectively.

Step 6: Solve the eigenvalue equation in Eq. (17). Sort their eigenvectors [w₁, w₂, …, w_di] according to their associated eigenvalues: λ₁≥λ₂≥…≥λ_di.

Step 7: Obtain W_i=[w₁, w₂, …, w_di] as the projection matrix associated with ith manifold.

4 Experiments

We performed our experiments using two subsets from the FERET database [24]: 1) FERET-1 is a randomly selected subset of the FERET database contains 400 gray-level face images from 200 persons with various facial expressions. Images labeled Fa, are used for training and images labeled Fb are used for test that some of these images are shown in Fig. 7. 2) Another subset of FERET database consists of 1800 images from 200 persons with facial pose angles range from +60° to –60°. Each image labeled ba is used for training and the other images labeled bb, bc, bd, be, bf, bg, bh and bi are used for test. Figure 8 shows pose variations of one subject from FERET subset. Also, four subsets of 400 images from the AR data base [25] were used. Subsets A to D are collected in the first session with neural, smile, anger and scream expression, respectively. We used a subset A as training image set and the remaining three subsets as test set. Figure 9 shows these four subsets of the AR data base. The face regions of all images are manually cropped, aligned and resized into 60×60 pixels according to eyes’ positions. All experiments are performed on a 32-bit system with a 2.2 GHz CPU and a 3 GB RAM using MATLAB 7.13. In the experiments, for the proposed SLPMM, we applied the minimum distance classifier for its simplicity, and the Euclidean and Mahalanobis metrics were used as distance measure.

Table 1 shows the recognition rate of different methods on FERET-1 database. Also, we compared the proposed SLPMM with two DCT based methods in DCT domain in Fig. 10 using three classification approaches: nearest neighbor with Euclidean distance measure, nearest neighbor with Mahalanobis distance measure and the reconstruction-based method which is presented in Ref. [19]. Tables 2 and 3 list the recognition rates of different methods on AR database in spatial and DCT domain, respectively. Table 4 shows the rank-1 recognition rate of different methods on the FERET subset across pose variations using the nearest neighbor classifier. It can be observed from these experiments (Tables 1–4 as well as Fig. 10) that our proposed SLPMM has a good performance in normal facial variations. Although, in severe variations the DMMA algorithm gained a slightly better performance such as: scream facial expression, +60° and –60° pose angles, the SLPMM makes reasonable results. We evaluate different size of parameters including k₁, k₂, local image patch and DCT feature vector, of our proposed method using the FERET-1 data set and the nearest neighbor classifier with Mahalanobis criterion. The influence of parameters: image patch size and DCT coefficient sub-block size as well as k₂ and k₁ are plotted in Figs. 11–14, respectively.

Fig. 7 FERET-1 sample images:

Fig. 8 FERET sample images for different poses of one subject

Fig. 9 AR sample images

It can be concluded that the proposed SLPMM shows a nearly stable performance versus varying these parameters compared with other methods. Thus the parameters k₁, k₂, local patch and DCT feature vector of the proposed SLPMM can empirically tune to be 14, 4, 10×10 and 5×5, respectively. There is another way to determine the exact size of k₁ and k₂ parameters without using any experiments, based on our work on I-DMMA [21]. Since using the I-DMMA automatic method for finding K₁ and K₂ does not considerably affect the recognition results in SLPMM, we ignore to mention the results. Table 5 tabulates the CPU time spent on the training and recognition phases in AR data base and nearest neighbor classifier by our proposed method compared with some of the SSPP face recognition methods. In real applications, only the recognition phase is an online process and the training phase is offline.

Table 1 Recognition accuracy (%) in FERET-1

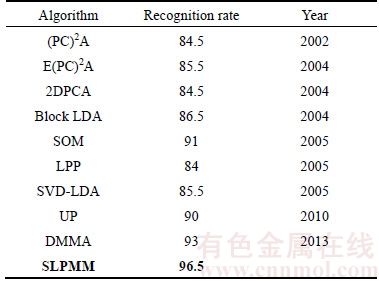
Fig. 10 Performance analysis of methods in DCT domain

Table 2 Recognition accuracy (%) on AR using pixel features

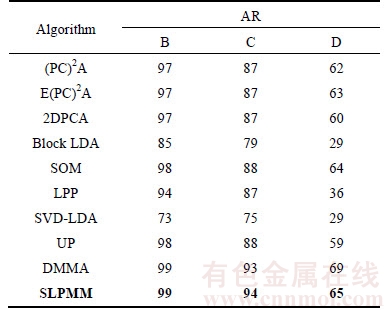
Table 3 Recognition accuracy (%) on AR using frequency features

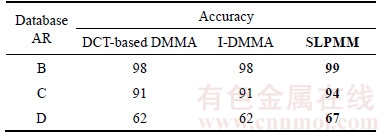
Table 4 Recognition accuracy on FERET versus pose differences

Fig. 11 Local patch size parameter analysis

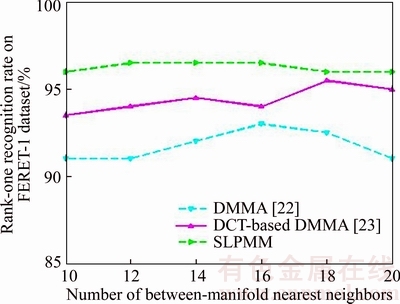
Fig. 12 DCT coefficient sub-block size parameter analysis

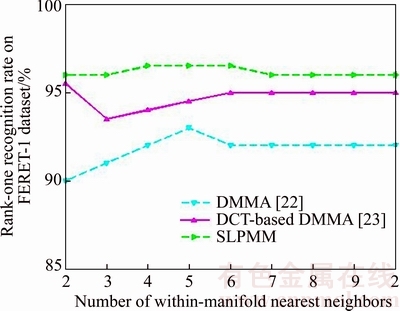
Fig. 13 Within-manifold nearest neighbors size analysis

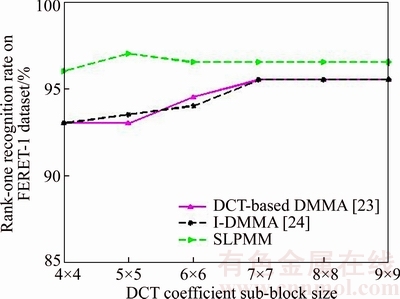
Fig. 14 Between-manifold nearest neighbors size analysis

Table 5 Computational time of different methods

Since the recognition phase of our method is a low time process, the performance efficacy of our proposed method in real applications may be good.

5 Conclusions

A novel feature extraction method is presented to address one sample problem. We propose to use Laplacian within-manifold matrix associated with intra-manifold matrix and Laplacian between-manifold matrix associated with inter-manifold matrix, under the maximization multimanifold margin framework. It is shown that since practical solutions of the SSPP problem rely on the information extracted from every single image as features, using more discriminative features such as DCT coefficients are useful. In the future work, we will concentrate on the robustness of our proposed method in severe face variations to increase the recognition accuracy.

References

[1] TURK M, PENTLAND A. Eigenfaces for recognition [J]. Journal of Cognitive Neuroscience, 1991, 3: 71–86.

[2] BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection [J]. IEEE Transaction Pattern Analysis and Machine Intelligence, 1997, 19: 711–720.

[3] TAN X, CHEN S, ZHAU Z H, ZHANG Z. Face recognition from a single image per person: A survey [J]. Pattern Recognition, 2006, 39: 1725–1745.

[4] WU J, ZHOU Z. Face recognition with one training image per person [J]. Pattern Recognition Letters, 2002, 23: 1711–1719.

[5] CHEN S, ZHANG D, ZHOU Z. Enhanced (PC)²A for face recognition with one training image per person [J]. Pattern Recognition Letters, 2004, 25: 1173–1181.

[6] YANG J, ZHANG D, FRANGI A, YANG J. Two-dimensional PCA: A new approach to appearance-based face representation and recognition [J]. IEEE Transaction Pattern Analysis and Machine Intelligence, 2004, 26: 131–137.

[7] DENG W, HU J, GUO J, CAI W, FENG D. Robust, accurate and efficient face recognition from a single training image: A uniform pursuit approach [J]. Pattern Recognition, 2010, 43: 1748–1762.

[8] WANG J, PLATANIOTIS K N, VENETSANOPOULOS A N. On solving the face recognition problem with one training sample per subject [J]. Pattern Recognition, 2006, 39: 1746–1762.

[9] CAN M, SHAN S, SU Y, CHEN X, GAO W. Adaptive discriminant analysis for face recognition from a single sample per person [C]// Automatic Face & Gesture Recognition and Workshops. Santa Barbara, CA: IEEE Press, 2011: 193–199.

[10] CAN M, SHAN S, SU Y, XU D, CHEN X. Adaptive discriminant learning for face recognition [J]. Pattern Recognition, 2013, 46: 2497–2509.

[11] YIN H, FU P, MENG S H. Sampled FLDA for face recognition with single training image per person [J]. Pattern Recognition, 2006, 39: 2443–2445.

[12] ZHANG D, CHEN S, ZHOU Z. A new face recognition method based on SVD perturbation for single example image per person [J]. Applied Math and Computation, 2005, 163: 895–907.

[13] GAO Q, ZHANG L, ZHANG D. Face recognition using FLDA with single training image per person [J]. Appl Math Comput, 2008, 205: 726–734.

[14] CHEN S, LIU J, ZHOU Z. Making FLDA applicable to face recognition with one sample per person [J]. Pattern Recognition, 2004, 37: 1553–1555.

[15] TAN X, CHEN S, ZHOU Z, ZHANG F. Recognizing partially occluded, expression variant faces from single training image per person with SOM and soft K-NN ensemble [J]. IEEE Trans Neural Networks, 2005, 16: 875–886.

[16] KANAN H, FAEZ K, GAO Y. Face recognition using adaptively weighted patch PZM array from a single exemplar image per person [J]. Pattern Recognition, 2008, 41: 3799–3812.

[17] TENENBAUM J B, SILVA V, LANGFORD J. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290: 2319–2323.

[18] ROWEIS S, SAUL L. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290: 2323–2326.

[19] LU J, TAN Y, VANG G. Discriminative multimanifold analysis for face recognition from a single training sample per person [J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2013, 35: 39–51.

[20] NABIPOUR M, AGHAGOLZADEH A, MOTAMENI H. A DCT-based multimanifold face recognition method using single sample per person [C]// The 8th Symposium on Advances in Science and Technology. Mashhad, Iran, 2014.

[21] NABIPOUR M, AGHAGOLZADEH A, MOTAMENI H. Multimanifold analysis with adaptive neighborhood in DCT domain for face recognition using single sample per person [C]// 22nd Iranian Conference on Electrical Engineering. Tehran, Iran: ICEE, 2014: 925–930.

[22] HE X, YAN S, HU Y, NIYOGI P, ZHANG H J. Face recognition using Laplacian faces [J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2005, 27: 328–340.

[23] YANG W, SUN C H, ZHANG L. A multi-manifold discriminant analysis method for image feature extraction [J]. Pattern Recognition, 2011, 44: 1649–1657.

[24] PHILLIPS P, WECHSLER H, HUANG J, RAUSS P. The FERET database and evaluation procedure for face recognition algorithms [J]. Image and Vision Computing, 1998, 16: 295–306.

[25] MARTINEZ A M, BENAVENTE R. The AR face database [R]. CVC Tech Rep, 1998–06.

(Edited by FANG Jing-hua)

Cite this article as: Nabipour Mehrasa, Aghagolzadeh Ali, Motameni Homayun. A supervised multimanifold method with locality preserving for face recognition using single sample per person [J]. Journal of Central South University, 2017, 24(12): 2853–2861. DOI:https://doi.org/10.1007/s11771-017-3700-9.

Received date: 2016–07-11; Accepted date: 2017–08-15

Corresponding author: Aghagolzadeh Ali, Professor, PhD; Tel: +9832311121; E-mail: aghagol@nit.ac.ir