混凝土箱梁水化热温度徐变应变分析
秦煜1,刘来君1,张柳煜1,铁明亮2
(1. 长安大学 公路学院,陕西 西安,710064;
2. 中国石油天然气管道工程有限公司,河北 廊坊,065000)
摘要:针对桥梁设计中混凝土箱梁水化热温度应变难以精确分析的现象,基于预制梁场混凝土箱梁水化热温度应变现场试验,采用初应变增量有限元法建立混凝土箱梁水化热温度应变的弹性徐变理论隐式解法数值模型,分析实测水化热应变、温度徐变应变及温度弹性应变三者之间的差异,研究混凝土箱梁水化热温度应变受徐变影响的规律。研究结果表明:拆模后箱梁顶板、底板水化热温度应变均为压应变且算术平均值基本一致;混凝土箱梁顶板水化热温度应变变化速率略小于底板水化热温度应变变化速率;徐变对混凝土箱梁水化热温度应力应变影响非常大,实际应变仅约为温度弹性应变的一半,因此,早龄期混凝土结构温度弹性应力减半更符合实际情况;混凝土箱梁水化热温度应变实测数据略大于温度徐变应变计算值,说明本文数值模型可准确有效模拟箱梁水化热温度应变真实状态、有助于桥梁分析设计。
关键词:温度徐变应变;混凝土箱梁;水化热;弹性徐变理论
中图分类号:U441.5 文献标志码:A 文章编号:1672-7207(2012)08-3250-07
Thermal creep strain of hydration heat on concrete box girder
QIN Yu1, LIU Lai-jun1, ZHANG Liu-yu1, TIE Ming-liang2
(1. School of Highway, Chang’an University, Xi’an 710064, China;
2. China Petroleum Pipeline Engineering Corporation, Langfang 065000, China)
Abstract: Field test of hydration heat on prefabricated concrete box girder was carried out to study the temperature strain of hydration heat on prefabricated concrete box girder. The numerical model of elastic creep theory with implicit method about temperature strain of hydration heat was established by the increment of initial strain method. On the basis of field test and numerical model, the difference among test data of hydration heat strain, thermal creep strain and thermal elastic strain was contrasted and analyzed. The influence of creep on temperature strain of hydration heat on concrete box girder was studied. The results show that the arithmetic means of compression strain on roof and floor are basically coincident after form removal. The change rate of compression strain on roof is slightly lesser than that of floor of concrete box girder. The influence of creep on temperature strain of hydration heat is great. And test value of strain is only about half of thermal elastic strain, so the influence of creep on hydration heat stress should be considered. The test value of hydration heat strain is slightly higher than calculated value of thermal creep strain. So this numerical calculation is reliable and well tally with the actual situation.
Key words: thermal creep strain; concrete box girder; hydration heat; elastic creep theory
混凝土箱梁浇筑硬化过程中,水泥水化反应会产生大量的水化热,导致箱梁温度场处于不稳定状态。受到约束时,混凝土箱梁温差会产生温度应力,引起早期裂缝,危及结构安全。同时,早龄期混凝土徐变性质十分明显,对箱梁温度应力应变又具有一定影 响[1]。因此,桥梁设计中往往难以精确分析混凝土箱梁水化热温度应力应变,设计考虑情况与工程实际不相符。关于混凝土结构水化热及温度徐变应力应变问题,国内外已进行了相关研究。Meinhard等[2]建立的基本水化模型确定了普通硅酸盐水泥水化时的热释放量及热释放率并将其适用范围扩大至其他类别混合水泥。冯德飞等[3]进行了混凝土箱梁水化热温度试验研究并绘制出混凝土水化热温度随观测时间变化的曲线。杨秋玲等[4]利用有限元软件Super SAP对大体积混凝土水化热温度场进行数值模拟计算。黄达海等[5]对碾压混凝土坝温度徐变应力仿真分析进展进行了研究。目前已有研究工作主要集中在混凝土水化热释放规律[2,6-8]、混凝土结构水化热温度场试验研究[3,9-10]及数值模拟[4,11-12]、大体积混凝土温度徐变应力数值计算[5,13-14]等,关于混凝土预制箱梁水化热温度徐变应变问题的研究较少。本文作者通过预制梁场混凝土箱梁水化热温度应变现场试验,采集箱梁水化热温度及应变实测数据,同时建立混凝土箱梁水化热温度徐变及温度弹性应变数值模型,研究实测水化热应变、温度徐变应变及温度弹性应变之间的差异,分析徐变对混凝土箱梁水化热温度应变的影响。
1 弹性徐变理论方程隐式解法
混凝土是弹性-徐变体,兼具弹性和徐变性质。混凝土徐变性质表现为应变徐变和应力松弛。弹性徐变理论由马斯洛夫和阿鲁久涅扬创立。该理论是以变形与应力之间成线性关系的假设为基础,应力变化时的徐变总变形可按相应应力增量引起的徐变变形总和来计算。为提高计算精度和效率,朱伯芳[15]提出了变应力作用下弹性徐变理论方程的隐式解法。
当应力连续变化时,t时刻徐变应变为:
 (1)
(1)
式中:σ(τ0)为时刻τ0的应力;C(t,τ)为徐变度。
从τ0时刻开始受力,到t时刻的混凝土徐变应变为:

式中:Δσ0为从τ0到τ1的应力增量。
当Δτi不大时,根据积分中值定理,在上式右边的积分项中,用中点龄期 的徐变度
的徐变度 代替 C(t,τ),得到:
代替 C(t,τ),得到:

 (2)
(2)
设混凝土徐变度可表示如下:

代入式(2),得到:

 (3)
(3)
取3个相邻时刻τn-1,τn和τn+1,时间步长为Δτn=τn-τn-1,Δτn+1=τn+1-τn。
由式(3),在上述3个时刻的徐变应变分别为:

 (4)
(4)

 (5)
(5)

 (6)
(6)
由式(4)和(5),得到:



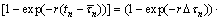


 (7)
(7)
同理:



 (8)
(8)
比较式(7)与式(8),得到如下递推公式:





2 混凝土箱梁水化热现场试验设计
2.1 工程概况
柳条河大桥位于甘肃省古浪县古丰乡,设计方案为等高度且左右分幅独立的装配式预应力混凝土连续箱梁桥,跨径为30 m,右幅16跨、左幅14跨。混凝土强度等级C50。根据《甘肃公路自然区划及环境参数研究报告》,柳条河大桥位于高原寒冷气候带。
2.2 测点布置
选取边箱梁距跨中1 m处截面为试验观测断面。观测断面测点布置如图1所示。采用非接触红外测温仪观测混凝土箱梁外表面温度,测点编号(1-1)~(1-11)。预制混凝土箱梁时,已预埋温度传感器和混凝土应变计,编号分别为(2-1)~(2-7)和(3-1)~(3-2)。悬臂板一侧的腹板为外腹板,反之为内腹板。

图1 箱梁观测断面测点布置(单位:cm)
Fig.1 Test point arrangement in cross section of box girder
2.3 试验仪器
(1) 箱梁混凝土表面测点采用UT302B非接触红外测温仪,测温范围为:-32~550 ℃,显示精度为±1.8 ℃或±1.8%T(T为温度)。
(2) 温度传感器采用WRN型分度号K热电偶温度计,测温范围:-50~400 ℃,测温精度:(0.75%T±2.5) ℃。测试仪器采用TES-1310 数字式温度表,解析度为0.1 ℃,温度测量范围为-50~199.9 ℃,温度测量精度为±(0.3%T+1 ℃)。
(3) 混凝土应变计采用长沙金码高科技实业有限公司生产的JMZX-215AT型,测量量程为-1 500 με~ 1 500 με。
2.4 数据采集
浇筑箱梁混凝土的入模平均温度为15.5 ℃。浇筑后即开始采集混凝土箱梁内部温度及应变数据,箱梁表面温度数据在拆模后开始采集。数据采集间隔周期为1 h,持续12 h。
3 数值分析模型建立
3.1 初应变增量有限元法
初应变法是理论严格的精确解法,仅存在离散误差,即空间域、时间域离散带来的近似性。基本假设为:结构为弹性—徐变体,即应变为瞬时弹性应变和徐变应变之和;徐变变形是线性的,即徐变变形与应力成正比;服从叠加原理,徐变变形可以叠加;徐变变形与受力状态无关,即认为拉压的徐变性质相同;徐变应力问题作为拟稳态问题处理。
初应变增量形式有限元法的计算步骤如下[1]:
(1) 单元增量位移。单元内任意一点的增量位移表示为:
 (9)
(9)
式中:Ne为单元形状函数矩阵;Δδe为一个单元的增量节点位移列阵。
(2) 单元增量应变(几何方程)为:
 (10)
(10)
式中:B为应变矩阵。
(3) 单元增量应力(物理方程)为:
 (11)
(11)
式中:D为弹性矩阵。此即为有限单元法中求应力的公式。
(4) 单元增量节点力为:



 (12)
(12)
其中:等效结点荷载为:
 (13)
(13)
 (14)
(14)
(5) 单元增量节点荷载为:

 (15)
(15)
式中:ΔF, 和Δf分别为作用于单元上的增量集中力,增量面力,增量体力荷载。
和Δf分别为作用于单元上的增量集中力,增量面力,增量体力荷载。
(6) 增量形式节点平衡方程为:
 ;
;
j=1,2,… (16)
3.2 数值模型
3.2.1 模型建立
利用有限元软件建立现场试验数值模型,对拆模后混凝土箱梁水化热温度弹性应变及水化热温度徐变应变进行数值模拟分析。基于弹性徐变理论方程隐式解法,编写子程序定义混凝土材料本构关系,采用初应变增量有限元法进行数值计算。模型中未考虑箱梁内部钢材的影响。通常认为桥梁沿桥跨方向温度相同,所以箱梁模型长度取1 m。混凝土箱梁有限元模型如图2所示。

图2 混凝土箱梁有限元数值模型
Fig.2 Finite element numerical model of concrete box girder
3.2.2 边界条件
时间边值条件:以拆模之前1 h混凝土箱梁各测点温度平均值作为初始温度。
空间边值条件:根据现场试验及传热学原理,本文考虑第一类边界条件,即已知箱梁各时刻温度。
应力场边界条件按竖直方向位移为0 m考虑。
3.2.3 参数选取
参考相似结构实测资料及文献[15],混凝土热特性参数取值如下:导热系数为3.0 J/(h·m·℃)、比热容为1 kJ/(kg·℃),热膨胀系数为1×10-5,密度为2 500 kg/m3;混凝土力学参数取值如下:泊松比为0.18,弹性模量为1.9×104 MPa。
4 结果分析
4.1 现场试验结果分析
拆模后混凝土箱梁观测断面各部位平均温度与周围环境大气温度实测数据对比如图3所示。
由图3可见,由于水化反应不断释放出水化热,混凝土箱梁表面及腹板中心平均温度均高于环境温度。受环境温度影响,箱梁各部位温度整体呈先升后降走势,并伴随着波动。在水化热及环境因素共同影响下,箱梁各表面按平均温度由高到低,依次为外腹板表面、顶板表面、内腹板表面。箱梁各部位中心平均温度,内腹板最高、底板最低、顶板及外腹板居中。因为受环境直接影响较小,以水化热作用为主,所以内腹板混凝土中心温度最高。
4.2 应变计算与试验结果对比分析
实测应变为水化热温度及环境因素作用下,由箱梁混凝土弹性变形、徐变、收缩等组成的应变实测值。温度徐变应变为由弹性变形、徐变变形2部分组成的温度应变计算值。温度弹性应变,即温度作用在混凝土箱梁瞬时产生的弹性应变计算值。
混凝土箱梁观测断面测点3-1和3-2处的实测应变、温度徐变应变、温度弹性应变对比分析分别如图4和5所示。
由图4和5可见:箱梁顶板、底板压应变的算术平均值基本一致。由于早龄期混凝土自收缩及干燥收缩等原因,实测应变数据略大于温度徐变应变计算值,约为后者的107%。实测应变、温度徐变应变分别约为温度弹性应变的55.5%和52%,说明早龄期混凝土徐变对箱梁中水化热温度应变应力影响很大,实际应力应变仅约为弹性应力应变的一半。早龄期混凝土结构水化热温度效应分析应考虑徐变的影响。
混凝土箱梁顶板、底板中心水化热温度应变变化走势基本相同,大体呈正余弦曲线。临近环境温度最高时,箱梁水化热温度应变达到最小值且底板应变略小于顶板应变。由于风速等环境因素影响,与底板相比,箱梁顶板水化热温度应变变化速率较小。
表1 箱梁各测点温度、应变及环境温湿度实测数据
Table 1 Test data of test point and environmental temperature and humidity


图3 箱梁观测断面各部位平均温度及环境温度对比分析
Fig.3 Comparative analysis mean temperature on box girder and ambient temperature

图4 箱梁观测断面测点3-1处正应变数据对比分析
Fig.4 Comparative analysis of normal strain data on 3-1 test point

图5 箱梁观测断面测点3-2处正应变数据对比分析
Fig.5 Comparative analysis of normal strain data on 3-2 test point
5 结论
(1) 混凝土预制箱梁拆模后短期内,在环境因素影响及水化反应条件下,箱梁全截面均呈现压应变,且顶板与底板压应变的算术平均值基本一致。
(2) 早龄期混凝土徐变对箱梁水化热温度应力应变影响很大,实际应变仅约为弹性应变的一半,建议桥梁设计分析对混凝土箱梁水化热温度弹性应力减半考虑。由于早龄期混凝土自收缩及干燥收缩等材料特性影响,混凝土箱梁水化热实际应变略大于温度徐变应变计算值。
(3) 分析混凝土结构水化热温度应力应该考虑徐变影响,求解弹性-徐变体的应力,该计算结果更符合实际结果。
参考文献:
[1] 王润富, 陈国荣. 温度场和温度应力[M]. 北京: 科学出版社, 2005: 120-125.
WANG Run-fu, CHEN Guo-rong. Temperature field and temperature stress[M]. Beijing: Science Press, 2005: 120-125.
[2] Meinhard K, Lackner R. Multi-phase hydration model for prediction of hydration-heat release of blended cements[J]. Cement and Concrete Research, 2008, 38(6): 794-802.
[3] 冯德飞, 卢文良. 混凝土箱梁水化热温度试验研究[J]. 铁道工程学报, 2006(8): 62-67.
FENG De-fei, LU Wen-liang. Experimental research on hydration temperature of concrete box girder[J]. Journal of Railway Engineering Society, 2006(8): 62-67.
[4] 杨秋玲, 马可栓. 大体积混凝土水化热温度场三维有限元分析[J]. 哈尔滨工业大学学报, 2004, 36(2): 261-263.
YANG Qiu-ling, MA Ke-shuan. Analysis of massive concrete 3-dimensional finite element hydrated heat temperature field[J]. Journal of Harbin Institute of Technology, 2004,36(2): 261-263.
[5] 黄达海,宋玉普,赵国藩. 碾压混凝土坝温度徐变应力仿真分析的进展[J]. 土木工程学报, 2000, 33(4): 97-100.
HUANG Da-hai, SONG Yu-pu, ZHAO Guo-fan. Advancement of thermal creep stress analysis for RCC dam[J]. Journal of China Civil Engineering Journal, 2000,33(4): 97-100.
[6] Grutzeck M W, Atkinson S D, Roy D M. Mechanism of hydration of CSF in calcium hydroxide solutions, Proceedings of the first international conference on the use of fly ash, silica fume, slag and natural pozzolans in concrete[J]. American Concrete Institute, 1983(2): 643-664.
[7] Snelson D G, Wild S, O'Farrell M. Heat of hydration of Portland Cement-Metakaolin-Fly ash (PC-MK-PFA) blends[J]. Cement and Concrete Research, 2008, 38(6): 832-840.
[8] 肖佳, 金勇刚, 勾成福, 等. 石灰石粉对水泥浆体水化特性及孔结构的影响[J]. 中南大学学报: 自然科学版, 2010, 41(6): 2313-2320.
XIAO Jia, JIN Yong-gang, GOU Cheng-fu, et al. Effect of ground limestone on hydration characteristics and pore structure of cement pastes[J]. Journal of Central South University: Science and Technology, 2010, 41(6): 2313-2320.
[9] 张亮亮, 陈天地, 袁政强. 桥墩混凝土的水化热温度分析[J].公路, 2007(9): 66-69.
ZHANG Liang-liang, CHEN Tian-di, YUAN Zheng-qiang. Analysis of hydration temperature of bridge pier concrete[J]. Highway, 2007(9): 66-69.
[10] 阮静, 叶见曙, 谢发祥, 等. 高强度混凝土水化热的研究[J]. 东南大学学报: 自然科学版, 2001, 31(3): 53-56.
RUAN Jing, YE Jian-shu, XIE Fa-xiang, et al. Study on heat of hydration on high strength concrete[J]. Journal of Southeast University: Natural Science Edition, 2001, 31(3): 53-56.
[11] 王燕, 陈玉香, 凌道盛, 等. 桐柏电站混凝土基础水化热温度场有限元分析[J]. 岩石力学与工程学报, 2007, 26(增1): 3266-3270.
WANG Yan, CHEN Yu-xiang, LING Dao-sheng, et al. Finite element analysis of hydration heat temperature field in concrete foundation of tongbai power station[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 1): 3266-3270.
[12] O’Donnell J J, O'Brien E J. A new methodology for determining thermal properties and modelling temperature development in hydrating concrete[J]. Construction and Building Materials, 2003(17): 189-202.
[13] 刘宁, 刘光廷. 大体积混凝土结构随机温度徐变应力计算方法研究[J]. 力学学报, 1997, 29(2): 189-202.
LIU Ning, LIU Guang-ting. Methods for random thermal creep stress analysis of massive concrete structures[J]. Acta Mechanica Sinica, 1997, 29(2): 189-202.
[14] 刘杏红, 周创兵, 常晓林, 等. 考虑非线性徐变的混凝土温度裂缝扩展过程模拟[J]. 岩土力学, 2010, 31(6): 1995-2000, 2005.
LIU Xing-hong, ZHOU Chuang-bing, CHANG Xiao-lin, et al. Simulation of temperature crack propagation considering nonlinear creep of concrete[J]. Rock and Soil Mechanics, 2010, 31(6): 1995-2000, 2005.
[15] 朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999: 199-205.
ZHU Bo-fang. Thermal stresses and temperature control of mass concrete[M]. Beijing: China Electric Power Press, 1999: 199-205.
(编辑 赵俊)
收稿日期:2011-10-19;修回日期:2012-01-20
基金项目:国家西部交通建设科技项目(2009319812050);甘肃交通科技项目(2009-05)
通信作者:秦煜(1983-),男,甘肃敦煌人,博士研究生,从事混凝土桥梁时变效应研究;电话:029-82334879;E-mail:qqqqyyyyqy@163.com