A novel limiting strain energy strength theory

LIU Guang-lian(刘光连)

School of Mechanics & Electrical Engineering, Central South University, Changsha 410083, China

Received 10 August 2009; accepted 15 September 2009

                                                                                                 

Abstract: With applied dislocation theory, the effects of shear and normal stresses on the slide and climb motions at the same section of a crystal were analyzed. And, based on the synergetic effect of both normal and shear strain specific energies, the concept of the total equivalent strain specific energy (TESSE) at an oblique section and a new strength theory named as limiting strain energy strength theory (LSEST) were proposed. As for isotropic materials, the plastic yielding or brittle fracture of under uniaxial stress state would occur when the maximum TESSE reached the strain specific energy, also the expressions on the equivalent stresses and a function of failure of the LSEST under different principal stress states were obtained. Relationship formulas among the tensile, compressive and shear yield strengths for plastic metals were derived. These theoretical predictions, according to the LSEST, were consistent very well with experiment results of tensile, compressive and torsion tests of three plastic metals and other experiment results from open literatures. This novel LSEST might also help for strength calculation of other materials.

Key words: equivalent stress; total equivalent strain specific energy; limiting strain energy; failure function; strength theory

                                                                                                           

 

1 Introduction

Strength theory deals with the yielding of plastic materials or fracture of brittle materials, and its investigation could be tracked back to Galileo’s work in the 17th century. Ever since then, many scholars have made great efforts in describing the mechanism of failure of materials, hitherto, various yield criteria or strength theories have been proposed. Among them, the most well-established strength theories are Rankine’s, Tresca’s, Saint-Venant’s, von Mises’, and Coulomb-Mohr’s and so on, as summarized in Ref.[1-7].

However, strength theory is still a very complicated and hot topic to be studied. It has been pointed out by ZHEN et al[8] that there is great difficulty in using the methods of physical mechanics to explain the plasticity, strength, damage, fracture of solids. It has been more than 60 years since the proposal of dislocation theory, but it has still not been merged into mechanics quantitatively. YNAG[9] also has stated that a great number of the experts in solid mechanics have devoted themselves to research the procedure of deformation, damage, instability (or fracture) for materials under external load, but the problem has not been solved yet. ZHEN[10] also stated that it will make great progress in the research of strength theory combining methods of macroscopic, meso-mechanical and microscopic. The research of strength theory is also a frontier problem[10-11].

In fact, defects always exist in metallic materials at various states, but all previous theories on failure of the materials ignored this important aspect. Based on the effects of shear and normal stresses at a section on the sliding and climbing of dislocations, thus we propose a limiting strain energy strength theory (LSEST). Equivalent stresses of the LSEST under various principal stress states are evaluated, and the corresponding strength criteria are established. The relationship among tensile, compressive and shear yield strengths are also given.

2 Current existing strength theories

Maximum principal stress theory (Rankine)[4] assumes that when the maximum principal stress in the complex stress system reaches the elastic limit stress in simple tensile, failure occurs. The criterion of failure is thus[2]

 or                           (1)

where σ_c and σ_t are the experimental determined yield stresses for simple tension and compression, respectively.

Maximum shear stress theory (Tresca)[4] states that failure can be assumed to occur when the maximum shear stress in the complex stress system becomes equal to that at the yield point in the simple tensile test. The criterion of failure becomes[4]

                                (2)

Maximum principal strain theory (Saint-Venant)[4] assumes that failure occurs when the maximum strain in the complex stress system equals that at the yield point in the tensile test:

                         (3)

Maximum distortion energy theory (von Mises)[4] states that failure occurs when the maximum shear strain energy component in the complex stress system is equal to that at the yield point in the tensile test:

     (4)

Coulomb-Mohr failure theory can be considered a generalized form of the Tresca theory, which can be given as[6-7, 12]

                                (5)

YU et al[13-15] proposed the twin-shear yield criterion in 1961, which was further developed into twin-shear strength theory in 1985 and later the twin- shear unified strength theory in 1991. The expression of the twin-shear unified strength theory is shown as[2]

≤

   when  (6a)

≥

  when   (6b)

where  is the strength ratio of tension to compression; and b is a coefficient reflecting the effect of the other principal shear stresses on the strength of materials.

YAO et al[16] proposed a generalized non-linear strength theory. YUAN et al[17] proposed a generalized yield criterion for plastic metals. ZHANG and ECKERT[18] proposed an ellipse criterion based on the tensile fracture behavior of the bulk metallic glass materials. ZHU and LEIS[19] proposed the average shear stress yield (ASSY) criterion. CHRISTENSEN[3, 20] proposed a two-parameter yield/failure criterion for broad classes of homogeneous and isotropic materials. Other yield criteria for isotropic materials are also proposed by ALTENBACH[21], CAZACU and BARLAT[22], ZHOU[23], HU and WANG[24]. Most failure criteria selected stress or strain as a parameter to predict the failure behaviors of the materials, or even directly extracted their conclusions from experimental data. MAXWELL first proposed energy as the parameter to predict the failure of the materials in 1856[3]. BELTRAMI further suggested that the total energy can be used as general criterion[3]. FREUDENTHAL clearly realized that material failure in different material scales occurs in different forms simultaneously and only the energy concept is universal throughout all material scales[25]. XIE et al[26-28] have pointed out that the effect of energy dissipation must be considered when investigating the mechanical behavior of rocks; the rock deformation and fracture process can be well described from the viewpoint of energy; and a criterion is proposed for strength and abrupt structural failure of rock based on the concepts of energy dissipation and energy release.

However, current failure criteria are far from perfect; and they could not fit in some circumstances. For example, Rankine’s theory does not suit for combined stress state of tension and compression; and Saint-Venant’s theory does not consistent with experimental results on the failure of the materials under biaxial tension or compression. For materials with equal strength of tension and compression, according to those criteria proposed by Tresca, von Mises, Coulomb-Mohr, Yu, etc., the failure stress becomes infinity under an equitriaxial tension or compression (), indicating that none of the above-mentioned failure criteria could apply to those specific conditions. TANG et al[29] demonstrated that the strength of material fracture cannot be predicted rationally and exactly if the fracture occurred under a complex stress state by Mohr’s theory. Similarly, CHRISTENSEN[12] also demonstrated that the Coulomb-Mohr criterion and the Drucker-Prager criterion predict physically unrealistic behavior in some important stress states. Also, for the twin shear unified strength theory, a similar drawback has been pointed out by LIU[30].

The stress state of pure torsion is a typical tensile-compressive principal stress, the relationship among pure shear(τ_s), simple tensile(σ_t) and simple compressive(σ_c) yield strengths, according to most current existing failure criteria, should be a fixed value. For example, the Tresca’s theory and Mises’ theory can only be applied to materials with τ_s=0.5σ_t and τ_s=0.577σ_t, respectively. The ratio of the shear yield strength to tensile yield strength for plastic metals lies between 0.25 and 0.947[31] generally, indicating there is contradiction between theory calculation and experimental results.

3 Formulation of LSEST

Because of the thermal vibration of atoms and the influence of various factors during polycrystalline forming, working and using process, the polycrystalline materials are inevitable to induce defects to the metals, for example point defects (vacancy etc), and line defects (dislocation etc). YANG[9] considered that the fractures of solids are closely related to the defects and microstructure. Dislocation theory closely relates to mechanical properties of crystals such as plastic yielding and brittle fracture[32-33]. Furthermore, dislocations can be initiated and expanded locally under external force. Any movement of dislocations can be decomposed into sliding and climbing. The former is caused by shear stress and the corresponding motion is parallel to sliding plane, and the latter is caused by normal stress and the corresponding motion is perpendicular to the sliding plane. The climbing of dislocations is accompanied by the formation of point defects, so the work done by the applied external forces of climbing should be larger than the energy required for the formation of point defects. The energy required for the formation of the point defects is named as defect-forming energy, which is mainly due to the work done by the normal stresses. Fracture of materials includes three phases, i.e. nucleation, growth and propagation. The nucleation and growth of cracks are closely related to sliding caused by shear stresses. Shear stresses are responsible for the forming of cracks, while normal stresses are responsible for propagation of cracks thereafter.

Interactions among atoms in crystals are mainly metallic bonding forces, and the energy generated by the bonding force makes the crystals bonded. Under applied external forces, if the staggered-arrangement energy and the defect-forming energy increase continuously, the staggered-arrangement energy enlarges sliding of the defects and the defect-forming energy promotes the amount of the defects in crystals. Failure, i.e. yielding of plastic materials and fracture of brittle materials, will occur once accumulated energy reaches a critical energy of the crystal bonding force.

Both of shear stress and normal stress play important roles in the plastic yielding or brittle fracture of materials. On the other hand, the shear and normal stresses can interchange each other according to the stress analysis. Owing to negligible contribution of the radius of dislocation core, dislocation type and crystal size to the dislocation energy[33-34], the dislocation energy generated by the shear and normal stresses at a section of a representative element is used to describe the occurrence of failure. Therefore, a new strength theory could be established as follows.

The sum of the strain specific energy generated by the normal and shear stresses at an oblique section refers to total equivalent strain specific energy (TESSE). For isotropic materials, we hypothesize that plastic yielding or brittle fracture takes place if the maximum TESSE reaches the strain specific energy in uniaxial stress state. This hypothesis for predicting failure of materials is named as limiting total equivalent strain energy strength theory, shortened as limiting strain energy strength theory (LSEST).

When a representative element of cell cube is subjected to a pair of opposite normal stresses, the resulting strain specific energy v_{s, σ} is

                                (7)

According to the stress analysis, pure shearing stress (τ) exerted at a cell cube may be decomposed into positive stress (τ) applied to a pair of opposite faces and negative stress (-τ) applied to other pair of opposite faces. However, this transformation is not equivalent because deformation resulted from the shearing stress is inhomogeneous, while deformation resulted from the normal stress is homogeneous. If the shearing stress applied to the cell cube is decomposed into positive and negative stresses, according to Eq.(7) the strain specific energy is then calculated by the following formula:

            (8)

Clearly, the equivalent strain specific energy calculated from Eq.(8) is 1/(1+v) times as much as the actual strain specific energy under pure shearing stress. This corresponds to a loss resulted from the transformation due to inhomogeneous deformation related to the shear stress and homogeneous deformation related to the normal stress. If an oblique section of the cell cube is subjected to normal stress σ and total shear stress τ, the TESSE at the cell cube can be obtained by summing Eqs.(7) and (8) as follows:

         (9)

We denote the strain specific energy of failure of materials in uniaxial tensile or compressive stress states as  and the corresponding normal stress as σ₀. From Eq.(7) one can get

                                (10)

As a result, from Eqs.(9) and (10) the criterion condition to determine the occurrence of failure of materials according to the LSEST is

                               (11)

Substituting Eq.(10) for  into Eq.(11) yields

                           (12)

Eqs.(11) and (12) are the analytic formulae for determining failure of a material by the LSEST. The equivalent stress of LSEST σ_ri can be derived from Eq.(12) as

                        (13)

It is emphasized that the LSEST focuses on analysis of the resulting maximum TESSE at an oblique section with the normal and shear stresses, rather than the strain specific energy in the whole cubic cell body. This is an essential difference between the LSEST and other failure theories. In the LSEST, the failure of materials is determined according to the maximum TESSE resulted from all the stresses applied to an oblique section, which is consistent with the failure beginning from some spots in this material.

4 Derivation of equivalent stress under various principal stress states

4.1 Biaxial principal-stress states

As shown in Fig.1, for a cell cube in biaxial principal stress state, normal stress  and shearing stress  at an oblique section with angle α(≤α≤) can be expressed in terms of two principal stresses as follows:

         (14)

                     (15)

Substituting Eqs.(14) and (15) into Eq.(9), the TESSE  is obtained to be

           (16)

Fig.1 Normal stress and shearing stress at oblique section of cell cube under biaxial principal stress state

From Eq.(16),  is seen to be a function of the direction angle α. To obtain the extreme value of , we differentiate with respect to α and obtain

            (17)

          (18)

According to extreme value criterion, when ,  will arrive at its extreme value.

1) Biaxial tensile-compressive principal stress state

For this kind of stress state

σ₁＞1, σ₂＜0                                (19)

 can be expressed as

   (20)

Setting  in Eq.(20), one gets: , , .

Furthermore, when  and , there are

＞0                   (21)

＞0                  (22)

For the remaining , from Eq.(18) one gets

＜0                         (23)

Upon putting these values of  into Eqs.(13), (14) and (15), we obtain different results, which are shown in Table 1.

Table 1 Parameters under biaxial tensile-compressive principal stress state calculated according to LSEST

According to the LSEST, if  gets its maximum, equivalent stress meets the requirement. From

Table 1, the equivalent stress in biaxial tensile- compressive principal stress state is.

In a similar way, if taking  and  () as two tensile-compressive principal stresses, respectively, the equivalent stress becomes

(＞0, =0, ＜0)        (24)

2) Uniaxial and other biaxial principal stress states

For uniaxial and other biaxial principal stress states including uniaxial tension or compression, equibiaxial tension or compression, nonequibiaxial tension or compression, an analogous procedure as mentioned in analyses of biaxial tensile-compressive principal stress state indicates that their equivalent stress is equal to absolute value of their largest principal stress. Consequently, the equivalent stress in various plane principal stress states can be expressed as

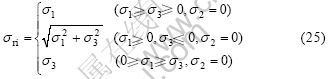
4.2 Triaxial principal stress states

A coordinate system (x, y, z) in which three axes are orientated in the directions of three principal stresses is selected as shown in Fig.2(a). For any oblique section N, new coordinates x′, y′, z′ are established as shown in Fig.2(b), in which the x′ axis is parallel to the N axis and the y′ and z′ axes are perpendicular to the N axis. The direction cosine values between three new axes and the original axes are shown in Table 2.

Fig.2 Cell body in action of principal stresses and oblique section N under original(a) and new(b) coordinates

Table 2 Direction cosine between new and original coordinate axes

In the new coordinate system, the stress components at the section, which across the point o′, are perpendicular to the x′, y′ and z ′ axes, respectively

                    (26a)

                   (26b)

                    (26c)

              (26d)

              (26e)

               (26f)

The relations between the direction cosine values in Table 2 are

                             (27)

The purpose of the LSEST is to calculate the extreme value of the TESSE resulted from the normal and shear stresses at a certain section. For some points under triaxial stress state, there are three sections which are perpendicular to x′, y′ and z′ axes, respectively. Let  v_{s, x}, v_{s, y} and v_{s, z} correspondingly represent the TESSE on these three sections. The following equations can be derived from Eqs.(9) and (26):

                 (28)

                 (29)

                 (30)

1) Equivalent stress on sections perpendicular to x′-axis

Substituting Eqs.(26a), (26d) and (26f) into Eq.(28), and through Eq.(27), we obtain

(31)

It can be found from Eq.(31) that the TESSE v_{s, x} is a function of l₁ and m₁. In order to get the maximum of  v_{s, x}, we differentiate v_{s, x} with respect to l₁ and m₁, respectively:

          (32)

         (33)

         (34)

      (35)

     (36)

From Eqs.(32) and (33), it can be seen that there are many examples of l₁ and m₁ which ensure that  and as follows.

(1) If  (equitriaxial stress state), then for any l₁ and m₁, the following equation can be obtained:

                (37)

This indicates that the total equivalent strain energy on any oblique section is a constant. From Eq.(31), it gives

                             (38)

Putting Eq.(38) into Eq.(13), the equivalent stress is

 ()                  (39)

In an equitriaxial stress state, the equivalent stress calculated according to LSEST is equal to the equivalent normal stress, which is consistent with that in equibiaxial stress state.

(2) If m₁=0,  can be derived from  in Eq.(32). Then, 0＜≤1 because of ≤1, and so , meaning triaxial tensile-

compressive principal stress state. Under such circumstances, from Eqs.(31), (34)-(36) and (13) the following equations are derived:

(＞0, ＜0, ≠0)       (40)

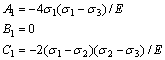
 (41)

The TESSE v_s,x gets its maximum because ＜0 and A₁＜0, which meets the requirement of the LSEST. It is the equivalent stress calculated according to Eq.(40) under triaxial tensile-compressive stress state according to LSEST and the obtained result is in agreement with that in biaxial tensile-compressive stress state.

(3) If l₁=m₁=0, then the equivalent stress is

 (0＞＞＞)                 (42)

(4) If l₁=0, under this condition, v_{s, x} has no extreme value and then the equivalent stress does not meet the requirement of the LSEST. But on an oblique section perpendicular to y′, it could be obtained from the analysis by the LSEST. 

(5) If , under this condition, Eqs.(32) and (33) are the symmetric equations of l₁ and m₁. Thus the TESSE reaches its maximum, and the equivalent stress is

(=＞0, ＜0)          (43)

 (6) If , the equivalent stress is

(＞0, =＜0)          (44)

2) Equivalent stress on oblique section perpendicular to y′ and z′ axes

In a similar manner to analyze the equivalent stress on sections which are perpendicular to the x′ axis, the equivalent stress under other triaxial principal stress states according to LSEST can be obtained as

(＞＞＞0)                   (45)

The equivalent stress of other triaxial principal stress states is the same as the above.

4.3 Equivalent stress of LSEST

According to Eqs.(25), (38), (40), (42)-(45) for the equivalent stress in uniaxial, biaxial and triaxial principal stress states, Eq.(46) of equivalent stress in various principal stress states can be obtained:

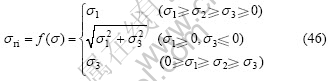
Under bending stress  and torsion stress , the equivalent stress according to Eq.(46) reads

                           (47)

The calculation results of the Mises’ theory, according to Eq.(4), is

                           (48)

5 Derivation of failure function

After we obtain the formulae for calculating the equivalent stress under principal stress states of tension, compression and tension-compression, the failure function will be further analyzed.

5.1 Tensile principal stress state

When the principal stresses are all tensile ones including uniaxial tensile, and (non)equibiaxial tensile, and (non)equitriaxial tensile, the equivalent stress according to the LSEST is equal to the maximum tensile stress. So, the LSEST implies that failure takes place when the maximum tensile stress  reaches either the yielding limit for plastic materials or the ultimate strength for the brittle materials (in the following, for convenience they are uniformly referred to as the tensile failure strength, denoted as), namely

 (≥≥≥0)                  (49)

or in terms of the failure function as

(≥≥≥0)             (50)

5.2 Compressive principal stress state

When the principal stresses are all compressive, the LSEST infers that failure takes place when  reaches either the yielding limit for plastic materials or the ultimate strength for the brittle materials (uniformly refers to as the compressive failure strength, denoted as), namely

 (0≥≥≥)                  (51)

or in terms of the failure function as

 (0≥≥≥)            (52)

5.3 Tensile-compressive principal stress state

Under any stress state of tensile-compressive principal stresses, the equivalent stress, according to LSEST, can all be expressed as

 (＞0, ＜0)             (53)

From Eq.(53), it is concluded that the equivalent stress under combined tensile-compressive principal stress states is composed of both tensile and compressive stresses. For materials with equal strength of tension and compression (), Eq.(53) can be used as the strength theory of the LSEST, while for materials with, Eq.(53) cannot be used anymore. In an alternative form, Eq.(53) can be rewritten as

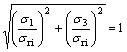 (＞0, ＜0)        (54)

When , Eq.(53) reduces to Eq.(49) and Eq.(54) reduces to Eq.(50). In this case, . In contrast, when, Eq.(53) reduces to Eq.(51) and Eq.(54) reduces to Eq.(52), implying. So, the failure function of materials in tensile-compressive principal stress state can be given as

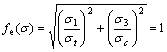 (＞0, ＜0)  (55)

5.4 Failure function in all and failure curve under various principal stress states

To sum up, the failure function of the LSEST can be expressed as

The failure condition is

≥1                                  (57)

From Eqs.(56) and (57), the failure curve under biaxial principal stress state () of the LSEST is shown in Fig.3. With the assumption of ＞ in  biaxial principal stress state, the failure curve of biaxial tensile-compressive principal stress state lies only in Quadrant Ⅳ. The failure curves of LSEST in the biaxial principal stress state are convex and have inflexions.

Fig.3 Failure curve under biaxial principal stress state in LSEST and experimental results of fracture strength (σ₂=0)

6 Experimental validations

6.1 Tensile principal stress state

The experiment data on fracture stresses of aluminum-silicon alloy ZL105 with σ₃/σ₁=0.268, 0.473, 0.700, and 1.000 in biaxial tensile principal stress state done by L? et al[35] as well as the failure curve of the LSEST are plotted in Fig.3 (QuadrantⅠ). The uniaxial tensile strength is σ_t=235.6 MPa. From Fig.3, the experiment results of the fracture stress are distributed around the failure curve of the LSEST in biaxial-tensile principal stress state. Results of L? et al[35] also shows that aluminum-silicon alloy ZL105 suffers brittle failure in biaxial tensile stress state, and the high tensile stress plays a dominant role, which almost has not been influenced by the other principal stresses, coinciding with predictions of the LSEST. L? et al[36] also studied the fracture of aluminum-silicon alloy ZL105 in biaxial equivalent tensile stress state, showing that the fracture stress is σ_x=σ_y=220.7 MPa, close to the fracture stress under longitudinal (or transversal) uniaxial tensile stress state σ_y=235.6 MPa (or σ_x=222.3 MPa).

The yield experiment of HJELM[37] on gray cast iron also demonstrated that the failure stress is nearly equal to the uniaxial tensile strength in a stress state of biaxial tension. The experiment results on ultimate strength of low carbon steel in triaxial equivalent tensile stress state done by engineering mechanics of Shanghai Jiao Tong University, China[38] indicated that the strength is the same as that under simple extension.

The above-mentioned results reveal that in tensile stress state, the failure strength of the materials is equal to the maximum principal stress, agreeing with the strength theory of the LSEST. It also coincides with the fact that the Rankine’s theory is usually applied to tensile-tensile stress state[39-41].

6.2 Tensile-compressive principal stress state

Pure shear stress state is a typical tensile- compressive principal stress state. Under pure shear stress state, plastic materials fail as a result of the action of shear stress. Pure shear stress state actually corresponds to a pair of tensile-compressive stress state with the same magnitude but opposite signs. According to the LSEST, using Eq.(55) the relationship among tensile, compressive and shear yield strengths, σ_t, σ_c, τ_s, can be derived as follows:

                             (58)

In particular, for the case of σ_t=σ_c, Eq.(58) gives

                               (59)

In order to validate the relationship among σ_t, σ_c and τ_s of some plastic metals from the LSEST, mechanical experiments on stress relief annealed A3 steel, T8 tool steel, brass 62 and so on were carried out. The size of specimens for standard tensile and torsion test is 10 mm in diameter, and the size of standard compressive specimens are of 30 mm in height. There were 4-5 specimens for each group under each test. The tensile and compressive tests were processed on an INSTRAN 8032 tester, and the torsion test was done on a torsion tester controlled by computerized torsion tester (CTT). The experimental results showed that A3 steel yielded in all three tests, T8 tool steel only yielded in tensile and compressive experiments. Apparent yielding did not occur in the torsion test of T8 tool steel and in all the three tests of Brass 62.

We took the upper yield limitation when yielding occurred or the value when 0.2% deformation happened as the failure strength of the material, which was taken as the average value of more than three effective experimental values. The values of tensile yield strength σ_t, compressive yield strength σ_c and torsion yield strength τ_s, and also the value of τ_sc according to Eq.(58) for the three plastic materials are listed in Table 3. The relative errors of τ_sc/τ_s are 1.78%, 0.09% and 2.82% for A3 steel, T8 tool steel and Brass 62, respectively, which indicated Eq.(58) that agreed with the experiment results very well, which are also highly in accordance with the experimental result of KONJUSHKO with five metal materials (Material 1-5) in Table 3[42].

Table 3 Experimental yield strengths of tension, compression and torsion and their calculated values of Eq.(58) of plastic materials

For materials with equal yielding strength of tension and compression (σ_t=σ_c), the shear yielding strength is 0.707 times tensile yield strength owing to Eq.(59). This is consistent with the experimental results of WINSTONE[43], who firstly found that at the initial yielding face of metal materials, the ratio of shear yielding stress to the tensile yielding stress is 0.7. However, it should be pointed out that this phenomenon cannot be explained by all existing failure theories except for LSEST.

In a tensile-compressive stress state, the maximum tensile stress or compressive stress from Eq.(55) is smaller than the stress under single tension or compression. This is consistent with the experimental results of L? et al[35], i.e., the ultimate tensile stress decreases slightly with an increase in the compressive stress component. The failure strengths of aluminum-silicon alloy ZL105 are σ_c=235.6 MPa and σ_t=-389.5 MPa in a stress state of uniaxial tension and compression, respectively. The experimental results on fracture stress of aluminum-silicon alloy ZL105 are shown in Fig.3 (Quadrant Ⅳ) in a biaxial tensile-compressive principal stress state[35]. From Fig.3, the measured fracture stresses are closely distributed around the failure curve of the LSEST in a biaxial tensile-compressive stress state. Minimum and maximum values are 0.783 and 1.130, respectively, and the average error between the experimental results and theoretic data calculated by Eq.(56), is about 3.5% (three groups of the experimental results related to σ₃/σ₁=-0.268 are exceptional and then discarded).

This indicates that in biaxial tensile state or biaxial tensile-compressive state, the calculated results according to the LSEST accord well with the experimental data, which is acceptable for prediction on mechanical properties. According to the strength theory of the LSEST (Eq.(56)) in tensile-compressive principle stress state, the tensile failure strength acts equally with the compressive failure strength in preventing failure of materials.

The above-mentioned results reveal that in biaxial tensile-compressive stress state, the calculation results of the LSEST agree with the experiments.

6.3 Compressive stress state

The yield experiment of HJELM[37] on gray cast iron also demonstrated that the failure stress is nearly equal to the uniaxial compressive strength in a stress state of biaxial compression. According to the LSEST, the strength theory in compressive stress state is equal to the maximum principal stress in magnitude. In calculating the strength in contact problem, the materials stand in a triaxial compressive stress state near the contact face and their three principal stresses are all compressive with almost equal values. The allowable compressive stresses in the contact face are much higher and even exceed 30% of the yielding stress of the materials[44], which is consistent with the LSEST. Under triaxial equivalent-compressive stress state, especially under hydrostatic stress, because of the specimen under actions of closed compressive stress, the amassed strain energy is difficult to release. Thereafter, plastic materials even brittle materials can sustain large compressive stress.

According to the LSEST, the failure of metals under all kinds of stress states has no relationship with the hydrostatic stress, which is in accordance with the experimental result of BRIDGMAN[45-46], who found that the failure of most metals is not affected by hydrostatic stress. The principal stress state remarkably influences the failure of materials and the failure of isotropic metals does not relate to the intermediate stress under different principal stress states. Based on the principle of the first stress invariant; and the sum of three principal stresses is constant in triaxial stress state, so only two of the three principal stresses are independent variables; and the intermediate stress cannot change the stress state essentially, which is consistent with the failure function of the LSEST.

6.4 Comparison between experimental data and other strength theories

1) Plastic materials under pure torsion stress

Under pure torsion stress, the experimental failure stress of plastic materials is the yield shear one. By comparing the theoretical calculated shear stress with the experimental shear stress, the relative error is obtained.

For plastic materials under pure torsion stress, the relative error from Tresca’s criterion, according to Eq.(2), is

                     (60)

The relative error from von Mises’ criterion, according to Eq.(4), is

                    (61)

As the tensile and compressive strengths are obtained from experimental data, the relative error from Mohr-Coulomb’s criterion, according to Eq.(5) is also considered:

            (62)

Based on Table 3 and Eqs.(60)-(62), the relative error of plastic materials under pure torsion stress according to other related strength theories is listed in Table 4.

Table 4 Relative error of plastic materials under pure torsion stress according to other related strength theories

From the relative error in Table 3 and Table 4, for 8 plastic materials under pure torsion, the average value of the calculated relative error, according to Tresca criterion, von Mises criterion, Mohr-Coulomb criterion and LSEST are -36.85%, -27.08%, -23.29% and 3.99%, respectively.

2) Aluminum-silicon alloy ZL105 under biaxial tensile- compressive principal stress

L? et al[35] obtained the experimental fracture stress of aluminum-silicon alloy ZL105 under several groups of biaxial tensile-compressive principal stress. Generally, the Treesca criterion and the von Mises criterion are considered to be applied to strength calculation of plastic materials, which cannot be applied to the strength calculation of aluminum-silicon alloy ZL105; however, the Rankine theory can only be applied to tensile or compressive stress state. So, the relative error of these three criterions is not considered here.

Under plane tensile-compressive principle stress, the relative error of Mohr-Coulomb criterion, according to Eq.(5), is

              (63)

The relative error of LSEST, according to Eq.(56), is

       (64)

According to the 21 groups of experimental fracture stresses of aluminum-silicon alloy ZL105 under biaxial tensile-compressive principal stress by L? et al[35], the average value of the calculated relative error of Mohr-Coulomb criterion and LSEST, according to Eqs.(63) and (64), are 28.4% and -3.5%, respectively.

3) Failure curves of several strength theories under plane stress state

Under uniaxial and plane stress, the failure curve of Rankine theory, Tresca criterion, von Mises criterion, Mohr-Coulomb criterion and LSEST as well as the experimental data is shown in Fig.4.

Fig.4 Failure curves of several strength theories under plane stress state

From Eqs.(1), (4), (5), (56) and Fig.4:

(1) Under uniaxial or biaxial tensile stress, the failure curve is in Quadrant Ⅰ, and the calculation results of LSEST is the same as those of Rankine theory, Tresca, von Mise and Mohr-coulomb theory. The calculation result of von Mises is larger than that of other four theories.

(2) Under uniaxial or biaxial compressive stress, the failure curve is in Quadrant Ⅲ, and the calculation result of LSEST is the same as that of Rankine theory and Mohr-Coulomb theory. The calculation results of Tresca, von Mises criterion are smaller than those of the other three theories.

(3) Under biaxial tensile-compressive stress state, the failure curve is in Quadrant Ⅱ or Ⅳ. The calculation results of Tresca theory, vol Mises theory, Mohr-Coulomb theory, LSEST, Rankine theory are different. Rankine theory cannot be applied to biaxial tensile-compressive strength calculation. So, under biaxial tensile-compressive principal stress state, the calculated failure value of LSEST is the largest, and materials can be most fully used.

From the above comparison of calculated results of several strength theories, under different principal stress state, LSEST has the highest calculation accuracy.

7 Conclusions

1) Based on the different effects of the shear and normal stresses at an oblique section on sliding and climbing of the dislocations, the total equivalent strain specific energy (TESSE) is constructed and then the limiting strain energy strength theory (LSEST) is proposed. For isotropic materials, failure meaning plastic yielding or brittle fracture occurs if the maximum TESSE arrives at or exceeds the strain specific energy of the plastic yielding or brittle fracture in uniaxial stress state.

2) The equivalent stresses of the LSEST in uniaxial, biaxial or triaxial stress states are calculated using the stress analysis of a cell body. The failure function under different stress states and the relationship among σ_t, σ_c and τ_s for metals are obtained.

3) Theoretical predictions agree well with the experimental results of the tension, compression and torsion of A3 steel, T8 tool steel and Brass 62, as well as other existing experimental results from literatures. Furthermore, the LSEST accounts precisely for the fact that the ratio of the initial shear yielding strength to the tensile yielding strength of plastic metals is 0.7. All these indicate the validness and universality of the LSEST in analyzing the failure of both plastic and brittle metals. In particular, in single tensile or compressive stress state, the LSEST is reduced to Rankine’s theory.

4) The equivalent stress under the actions of bending and torsion according to the LSEST is lower that calculated data according to Mises criterion.

 

References

[1] THEOCARIS P S. Failure criteria for isotropic bodies revisited [J]. Eng Fract Mech, 1995, 51: 239-264.

[2] YU Mao-hong. Advances in strength theories for materials under complex stress state in the 20th century [J]. Appl Mech Rev, 2002, 55: 169-218.

[3] CHRISTENSEN R M. A two-property yield, failure (fracture) criterion for homogeneous, isotropic materials [J]. J Eng Mater Tech, 2004, 126: 45-52.

[4] HEARN E J. Mechanics of materials (Volume 1) (2nd Edition) [M]. England Oxford: Pergamon Press, 1985: 401-414.

[5] HIBBELER R C. Mechanics of materials (Fifth Edition) [M]. USA, New Jersey: Prentice Hall, 2003: 524-529.

[6] BUDYNAS R G. Advanced strength and applied stress analysis (2nd Edition) [M]. New York: McGraw-Hill, 1999: 505-515.

[7] GOU Wen-xuan. Material mechanics Ⅰ [M]. Beijing: Science Press, 2005: 296-309. (in Chinese)

[8] ZHEN Ze-min, ZHOU Heng, ZHANG Han-xin, HUANG Ke-zhi, BAI Yi-long. Trends of development in mechanics in the early 21st century [J]. Advances in Mechanics, 1995, 25(4): 433-441. (in Chinese)

[9] YANG Wei. Outstanding problems in the failure theory of solids [J]. Chinese Quarterly of Mechanics, 1998, 19(4): 289-296. (in Chinese)

[10] ZHEN Ze-min. Mechanics in the 20-21st century [J]. World Sci-Tech R & D, 1995(1): 11-14. (in Chinese)

[11] TU Shan-dong, ZHAO Yong-xiang. Development trends of mechanical strength [J]. Journal of Mechanical Strength, 2005, 27(4): 554-559. (in Chinese)

[12] CHRISTENSEN R M. A comparative evaluation of three isotropic, two property failure theories [J]. J Appl Mech, 2006, 73: 852-859.

[13] YU Mao-hong. Twin shear stress yield criterion [J]. Int J Mechanical Science, 1983, 25(1): 71-74.

[14] YU Mao-hong, HE Li-nan, SONG Ling-yu. Twin shear stress theory and its generalization [J]. Science in China, Ser A, 1985, 28(11): 1174-1183.

[15] YU Mao-hong, HE Li-nan. A new model and theory on yield and failure of materials under complex stress state [C]// INOUE J M. Mechanical Behaviour of Materials-VI, Vol 3. Oxford: Pergamon Press, 1991: 841-846.

[16] YAO Yang-ping, LU De-chun, ZHOU An-nan, ZOU Bo. Generalized non-linear strength theory and transformed stress space [J]. Science in China, Ser E, 2004, 47(6): 697-709.

[17] YUAN Shi-jian, XIAO Da-zhi, HE Zhu-bin. A generalized yield criterion [J]. J Mater Sci Technol, 2004, 20(6): 800-802.

[18] ZHANG Z F, ECKERT J. Unified tensile fracture criterion [J]. Phys Rev Lett, 2005, 94: 094301.

[19] ZHU Xian-kui, LEIS B N. Average shear stress yield criterion and its application to plastic collapse analysis of pipelines [J]. International Journal of Pressure Vessels and Piping, 2006, 83: 663-671.

[20] CHRISTENSEN R M. A comprehensive theory of yielding and failure for isotropic materials [J]. J Eng Mater Tech, 2007, 129: 173-181.

[21] ALTENBACH H, ZOLOCHEVSKY A. A generalized failure criterion for three-dimensional behavior of isotropic materials [J]. Engineering Fracture Mechanics, 1996, 54(1): 75-90.

[22] CAZACU O, BARLAT F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals [J]. Int J Plast, 2004, 20: 2027-2045.

[23] ZHOU Xiao-ping, ZHANG Yong-xing, WANG Jian-hua. A new nonlinear yield criterion [J]. Journal of Shanghai Jiaotong University (Science), 2004, E-9(1): 31-33.

[24] HU Wei-long, WANG Z R. Multiple-factor dependence of the yielding behavior to isotropic ductile materials [J]. Computational Materials Science, 2005, 32: 31-46.

[25] LI Q M. Strain energy density failure criterion [J]. International Journal of Solids and Structures, 2001, 38: 6997-7013.

[26] XIE He-ping, PENG Rui-dong, JU Yang. Energy dissipation of rock deformation and fracture [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 3565-3570. (in Chinese)

[27] XIE He-ping, PENG Rui-dong, JU Yang, ZHOU Hong-wei. On energy analysis of rock failure [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2603-2608. (in Chinese)

[28] XIE He-ping, JU Yang, LI Li-yun. Criteria for strength and structure failure of rocks based on energy dissipation and energy release principles [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24: 3003-3010. (in Chinese)

[29] TANG An-min, HAN Xing-ming. Brittle material damage and Mohr’s theory [J]. Mechanics in Engineering, 2004, 26(2): 47-48. (in Chinese)

[30] LIU Guang-lian. Uniqueness in calculating the strength of plastic metals based on the twin-shear unified strength theory [J]. Journal of Central South University: Science and Technology, 2008, 39(6): 1280-1284. (in Chinese)

[31] YU Mao-hong. Twin-shear theory and its applications [M]. Beijing: Science Press, 1998: 59-113, 299-308. (in Chinese)

[32] HA Kuan-fu. Microtheory of metal mechanical properities [M]. Beijing: Science Press, 1983: 603-630. (in Chinese)

[33] YU Yong-ning. Theory of metallography [M]. Beijing: Metallurgy Industry Press, 2005: 278-336. (in Chinese)

[34] WAS G S. Fundamentals of radiation materials science: Metals and alloys [M]. Berlin Heidelberg: Springer, 2007: 267-321.

[35] L? Gui-ying, ZHANG Ze-hua. An experimental investigation of strength on Al-Si alloy ZL105 under complex stress states [J]. Mechanical Strength, 1989, 11(2): 75-77. (in Chinese)

[36] L? Gui-ying, ZHANG Ze-hua. An experimental investigation of the plastic behavior on Al-Si alloy ZL105 under bi-directional stress states [J]. Chinese Journal of Applied Mechanics, 1990, 7(2): 27-33. (in Chinese)

[37] HJELM H E. Yield surface for grey cast iron under biaxial stress [J]. J Eng Mater Tech, 1994, 116: 148-154.

[38] Engineering Mechanics Lab of Shanghai Jiao Tong University. Engineering Mechanics [M]. Beijing: People’s Education Press, 1976. (in Chinese)

[39] GENSAMER M. Strength of metals under combined stresses [C]// Twenty-second National Metal Congress and Exposition. Cleveland, OH: American Society of Metals, 1941.

[40] DORN J E. Effect of stress state on the fracture strength of metals [J]. Fracture of Metals, ASM, 1948: 32-50.

[41] PAUL B. Macroscopic criteria for plastic flow and brittle fracture [M]// LIEBOWITZ H. Fracture and advanced treatise vol.Ⅰ. New York: Academic Press, 1968: 313-496.

[42] GOKHFELD D A, SADAKOV O S, KONONOV K M. On the ultimate strain criterion for fracture prediction at normal and elevated temperatures [J]. Dynamics, Strength & Wear-resistance of Machines, 1997, 3: 12-18.

[43] WINSTONE M R. Influence of prestress on the yield surface of the cast nickel superalloy MARM002 at elevated temperature [C]// CARLSSON J, OHLSON N G. Proceedings of the 4th International Conference, Mechanical behavior of materials—1. Oxford: England, Swen Pergamon Press, 1984: 199-205.

[44] XU Hao. Machine design handbook Ⅰ [M]. Beijing: Mechanical Industry Press, 1991. (in Chinese)

[45] BRIDGMAN P W. The compressibility of thirty metals as a function of pressure and temperature [J]. Proc Am Acad Arts Sci, 1923, 58: 165-242.

[46] BRIDGMAN P W. The effect of hydrostatic pressure on the fracture of brittle substances [J]. J Appl Phys, 1947, 18: 246-258.

                     

Corresponding author: LIU Guang-lian; Tel: +86-731-88836906; Fax: +86-731-88836919; E-mail: glliu@mail.csu.edu.cn

DOI: 10.1016/S1003-6326(09)60084-4

(Edited by YANG Bing)