基于非等距预测模型的填土路基沉降量分析
唐葭1,刘霁1, 2,蒋建清1
(1. 湖南城市学院 土木工程学院,湖南 益阳,413000;
2. 中南大学 资源与安全工程学院,湖南 长沙,410083)
摘要:根据路基沉降量的实测资料,利用3种常用的灰色预测模型对路基沉降量变化规律进行分析及精度对比,选取预测精度最高的灰色预测模型预测路基最终沉降量。同时,基于改进灰靶决策理论,对路基沉降的影响因素进行综合分析,将靶心距与路基最终沉降量对应,利用非等距预测模型最终沉降量与靶心距之间的规律进行分析。研究结果表明:该模型可以揭示路基沉降与影响因素之间的量化关系,为路基沉降的预测与规律分析提供了新的思路与参考。
关键词:非等距预测模型;改进灰靶决策理论;精确度;沉降;填土路基
中图分类号:U416.1+11 文献标志码:A 文章编号:1672-7207(2014)06-2054-08
Fill subgrade settlement analysis based on prediction model of non isometric
TANG Jia1, LIU Ji1, 2, JIANG Jianqing1
(1. School of Civil Engineering, Hunan City University, Yiyang 413000, China;
2. School of Resources and Safety Engineering, Central South University, Changsha 410075, China)
Abstract: According to the measured results of roadbed settlement, the change law of settlement was analyzed and the accuracy was compared using three gray prediction models. The optimal gray prediction model was chosen to predict the final roadbed settlement, and modified gray target decision theory was used to comprehensively analyze the effect factors of roadbed settlement, then off-target distances were corresponded with roadbed final settlements. In addition, non-equidistant prediction model was employed to the law between final settlement and off-target distance. The results show that the model exhibits a good performance on quantitative relationship between roadbed settlement and its factors, which can provide reference for settlement prediction and law analyses of roadbed.
Key words: prediction model of non-isometric; modified gray target decision theory; accuracy; settlement; fill subgrade
公路路基沉降与公路的施工质量、公路建成后的服务水平及行车安全密切相关。然而,公路的沉降是一个缓慢而长期的过程,且其影响因素是多方面的,故对路基沉降量进行准确预测并找出路基沉降规律,对路基沉降的预防有着现实和重要意义[1-2]。对公路路基沉降的研究主要有2个方向:一是对路基的沉降量进行研究;二是对路基沉降的影响因素进行研究。对前者的研究一般是在收集原始数据的基础上,用各种预测理论建立符合或较符合沉降特征的模型对最终沉降量进行预测。目前,常用的路基沉降量预测方法主要有双曲线法和各种系统工程预测方法[3-7]。胡振南[3]采用双曲线法分析和预测了高速公路路基的沉降特性并对比实测沉降结果,证明了两者相对误差很小,论证了双曲线法在路基沉降预测中的适用性和高可靠性。夏江等[4]针对加固纠偏工程的沉降预测问题,运用MATLAB编写遗传算法程序进行了预测分析,计算结果与实测结果基本一致,证明了遗传算法在全局优化、非线性优化、多参数优化等方面表现出较传统算法较大的优势。然而,这些方法都存在一定的局限性,如双曲线法是将双曲线与实际沉降量进行近似拟合,实际沉降量要满足或者近似满足双曲线的特征规律,而实际上路基沉降都是在初期较大,后期较小,接近于“S”形曲线,因此,利用双曲线预测方法对公路路基沉降量进行预测时,往往与现实情况有较大偏差。且不论是双曲线预测还是各种系统工程预测,一般采用单一预测方法,没有进行多种预测方法的精度比较与优选,无法判定其优劣;而对路基沉降影响因素的相关研究,大多是对路基沉降因素进行定性分析,很少涉及各影响因素与路基沉降量之间的量化关系及二者之间内在规律的研究,在工程实践中难以得到应用。鉴于此,本文作者首先在统计与分析各路段路基早期沉降的基础上,建立3种常用的基于不同理论基础的预测模型[8-11],并优选出最佳预测模型预测最终沉降量;然后,利用改进灰靶决策理论[12-13]计算各路段路基沉降影响因素向量的靶心距计算。将靶心距与路基最终沉降量相对应,构建出符合其数据特征的非等距预测模型[14-15],得到路基沉降的影响指标与路基最终沉降量之间的规律,在高速公路研究段应用中检验效果良好,为路基沉降因素与路基沉降量之间进行量化分析提供一种新思路。
1 系统建模
1.1 路基沉降量预测
路基沉降量符合单变量(时间)的灰色预测模型,故选择较常用的符合正向累加数据特征的GM(1,1)模型、差分verhulst模型以及微分verhulst模型通过路基沉降量预测精度比较,选取精度最高的模型预测路基最终沉降量。其中,精度比较包括平均相对误差比较、残差平方和比较和后验差检验比较。设x(0)(k)为路基沉降观测的原始值或实际值,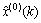 为3种预测模型的沉降预测值或理论值,n为路基沉降观测数据个数,则原始数据列和预测数据列的残差
为3种预测模型的沉降预测值或理论值,n为路基沉降观测数据个数,则原始数据列和预测数据列的残差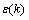 及相对误差
及相对误差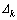 分别为
分别为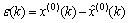 和
和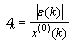 。
。
(1) 平均相对误差为
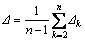 (1)
(1)
(2) 残差平方和为
s=εTε (2)
其中:ε为原始数据与理论值差向量。
(3) 后验差检验。
① 后验比值为
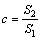 (3)
(3)
② 小误差概率为
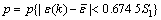 (4)
(4)
式中:S1和S2分别为原始数据和残差的均方差;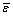 为残差的均值。可通过后验比值c和小误差概率p对预测模型精度进行综合评定[16-17],其评定等级见表1。模型精度评定等级越高,其预测精度也越高,可预测的时间或步长也越长。故选取平均相对误差最小、残差平方和最小、精度等级最高的模型对路基最终沉降量进行预测。
为残差的均值。可通过后验比值c和小误差概率p对预测模型精度进行综合评定[16-17],其评定等级见表1。模型精度评定等级越高,其预测精度也越高,可预测的时间或步长也越长。故选取平均相对误差最小、残差平方和最小、精度等级最高的模型对路基最终沉降量进行预测。
表1 灰色预测模型精度检验等级表
Table 1 Precision inspection level of grey forecasting model

1.2 路基沉降影响因素选取
根据相关学者的研究成果,路基沉降与多种因素有关,这些影响因素有如下几类[18]:
(1) 地基土性质。主要包括黏聚力、变形模量和内摩擦角,其中影响路基沉降的地基土性质是变形模量。通过研究发现,在其他影响因素不变的条件下,变形模量越大,路基沉降量越小。
(2) 路堤填筑高度。经过统计分析,可以认为路堤填筑高度越大,路基沉降量越大。
(3) 路堤填料。路堤填料的性质主要有黏聚力、变形模量、内摩擦角和容重,其中容重是影响路基沉降的主要因素。
(4) 施工时间。统计研究表明,施工时间对路基沉降影响不大。
(5) 地形地质条件。一般而言,地形地质条件对路基沉降有较大影响,但是,在实际路基施工中,往往会采取各种各样的工程技术措施减轻或消除不良地形地质条件对路基沉降的影响,因此,可以认为地形地质条件对路基沉降影响不大。
(6) 水文气候条件。地表水排泄,公路沿线河流常水位、洪水位、地表积水和积水时间等水文条件都会影响到路基路面的沉降稳定性。由于水文气候条件的复杂性,其对路基沉降的影响可以用综合评分值来反映。
(7) 路基填料。若路基填土中含有不良土质,则路基在荷载作用下就会产生沉陷破坏。路基填料的质量可由对路基填料质量的评分来表示。
(8) 施工设计与施工技术。虽然路基施工设计与施工技术对路基沉降有影响,但若对于同一公路,其施工设计与施工技术基本上是一样的,因此,可以忽略这因素对路基沉降的影响。
综上所述,选取地基土变形模量、路堤填筑高度、路堤填料容重,水文气候条件以及路基填料质量等因素作为路基沉降的影响因素。
1.3 改进灰靶决策分析
对于路基沉降各影响因素,有些因素指标本身就是数值指标,如地基土变形模量、路堤填筑高度以及路堤填料容重等;有些因素指标是人为评分指标,如水文气候条件以及路基填料质量。对于因素指标,其数值或者分值所反映的各路段沉降量的意义不尽相同,有些指标越大,而路基沉降量越大;有些指标越小,而路基沉降量越大。传统灰靶决策理论通过人为的方式确定局势的效果,而改进灰靶决策理论以因素指标本身的数值,通过灰色效果测度计算来确定。
对于路堤填筑高度以及路堤填料容重等数值越大,路基沉降越大的指标,采用灰色上限效果测度处理,则灰色上限效果测度处理值γup为
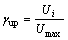 (5)
(5)
对于地基土变形模量、水文气候条件评分以及路基填料质量评分等越大,路基沉降越小的因素指标,采用灰色下限效果测度处理,则灰色下限效果测度处理值γdown为
 (6)
(6)
式中:Umax,Umin和Ui分别为各公路路段路基同类指标因素数值集合{Ui}中最大值、最小值以及一般值。
对于各公路路段路基,各指标因素经过灰色效果测度后的值就是局势sij在指标k下的具体效果值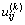 ,由此得到各公路路段路基在局势sij下的效果向量为
,由此得到各公路路段路基在局势sij下的效果向量为
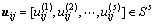 (7)
(7)
其中:Ss为s维超平面区域的决策灰靶,
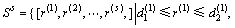
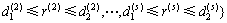 (8)
(8)
其中:r(1),r(2),…,r(s)为灰靶空间向量的维度;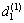 和
和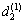 为灰靶在维度r上的取值范围。
为灰靶在维度r上的取值范围。
决策灰靶一般情况下都为S维空间内的类似于球形的灰靶,示意图见图1。
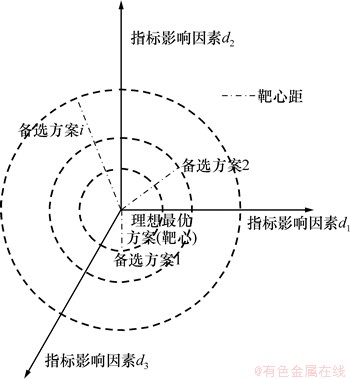
图1 灰靶决策球形模型
Fig. 1 Spherical model of gray target decision-making
其一般模型为
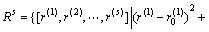
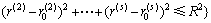 (9)
(9)
其中:Rs为多维空间下的球形粒度。靶心即为各路段路基影响指标因素灰色效果测度所反映的路基理论沉降最小路段灰色效果测度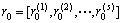 。
。
路段i的路基灰色效果测度向量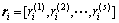 ,距离理论沉降最小路段的靶心距sDi为
,距离理论沉降最小路段的靶心距sDi为
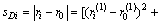
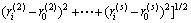 (10)
(10)
靶心距sDi反映了路段i路基的灰色效果测度评测情况ri与理想最优灰色效果测度评测情况r0的偏离程度,sDi越大,则表明相应的路段路基的沉降量也就越大。
1.4 非等距预测模型
以各路段路基影响指标的改进灰靶决策的靶心距作为自变量,以相应的各路段路基的最终沉降量作为因变量建立非等步距的预测模型,对路段路基沉降规律进行分析。由于是非等距的预测模型,因此,需要构造背景值,将非等距的自变量转换为等距的自变量然后建模进行预测。通过转换精度比较,模型采用修正精度高的最小二乘法对非等距自变量的等距关系进行转换。
设路段路基规律分析预测的非等距原始序列为
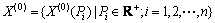 (11)
(11)
其中:X(0)(Pi)为各路段路基的最终沉降量;Pi为各路段路基影响因素灰色效果测度的靶心距。很显然,Pi为非等距的。
设定Pi′为等距序列,则有Pi′=m0+m1i,其中i∈N, m0与m1为待定系数。且要求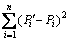 最小,这样就可以利用最小二乘法的线性拟合模型进行求解,得到m0和m1,进而得到Pi′,而X(0)( Pi’)则可根据X(0)(Pi)进行插值计算来求得。故转换后等距路段路基规律分析预测的等距原始序列为
最小,这样就可以利用最小二乘法的线性拟合模型进行求解,得到m0和m1,进而得到Pi′,而X(0)( Pi’)则可根据X(0)(Pi)进行插值计算来求得。故转换后等距路段路基规律分析预测的等距原始序列为
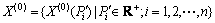 (12)
(12)
根据等距的原始数据序列,即可参照前面的各类预测模型进行预测求解。对于任意的路段路基靶心距值Pi,将其代入预测模型的时间响应序列即可求得相应的路基沉降量预测值。建模流程图如图2所示。
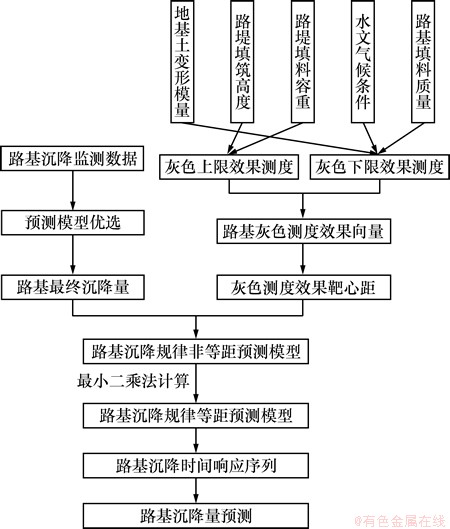
图2 沉降预测建模流程
Fig. 2 System modeling process
2 工程实例
2.1 工程背景
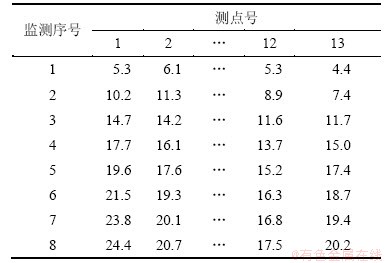
湖南地区某等级公路设计行车速度为80 km/h。由于工程线路较长,穿越的地层多种多样,因此,各路段的沉降量与沉降速率有明显差异。自工程开工以来,发现个别路段由于土质及所在地区的水文气候等原因,路基沉降较明显。为观测路基沉降,在全路段路基沉降特别明显的地段共设置13组监测点,从路基建成后每半月监测1次,共监测4月,所得结果如表2所示。
表2 路基沉降量监测结果
Table 2 Roadbed settlement monitoring cm
各监测点所在路段的地基土变形模量、路堤填筑高度、路堤填料容重,水文气候条件以及路基填料质量等因素指标如表3所示。
2.2 路基最终沉降量预测
根据表2中各路基路段的监测结果,对其进行基于GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型的模型精度比较并选取精度最高的预测模型进行预测。以1号监测点为例,GM(1,1)模型、微分Verhulst模型、差分Verhulst模型的参数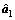 ,
,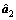 和
和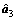 分别为:
分别为:
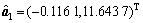
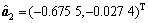
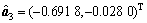
将各参数列分别代入各模型求解,得到各模型对1号监测点的理论预测值,并进行误差比较及精度检验,结果如表4所示。
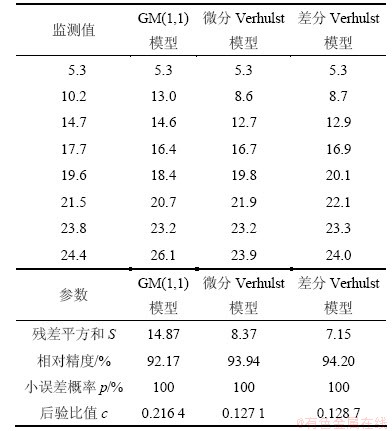
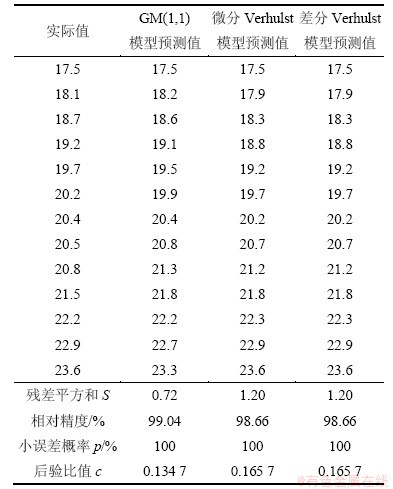
由表4并结合表1可知:对1号监测点沉降量进行预测时,GM(1,1)模型的预测精度为二级,微分Verhulst模型、差分Verhulst模型的预测精度为一级,差分Verhulst模型的误差精度略高于微分Verhulst模型。因此,采用差分Verhulst模型来对1号监测点路段路基的最终沉降量进行预测。类似地,对其余监测点,采用各模型精度进行比较并对路基最终沉降量进行预测,预测结果如表5所示。
表3 各路段指标因素数值统计表
Table 3 Index factors values tables of each section
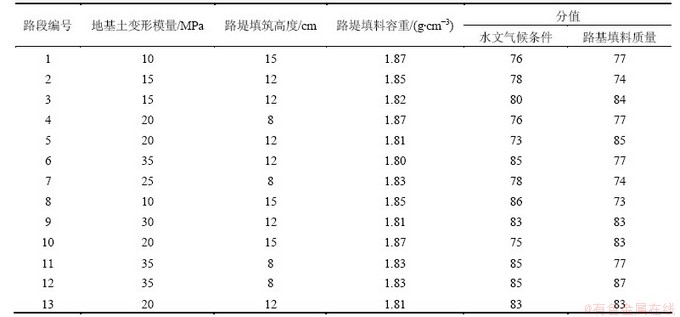
表4 各模型沉降量误差检验结果
Table 4 Error test settlements of each model cm
2.3 路基影响因素灰靶决策分析
根据前面的改进灰靶决策方法,计算各路段指标因素灰色效果测度,如表6所示。
由于各指标灰色效果测度越大,反映路基沉降量越大,因此,根据表6推断出各路段路基影响指标因素路基沉降最小的理论最小向量(靶心)为
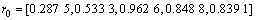
根据式(10),求得各路基路段的靶心距结果见表7。
2.4 非等距路基沉降规律分析
(1) 根据表5与表7,可以得到非等距预测模型的原始数据序列为:
P=(0.0189,0.1106,0.2065,0.2677,0.2757,
0.2883,0.3459,0.3746,0.4705,0.4963,0.5313,
0.8682,0.8687);
X(P)=(17.5,18.4,19.2,19.6,20.0,19.9,20.3,
20.4,20.5,20.6,20.9,24.7,24.8)
(2) 对P序列利用最小二乘法进行拟合,拟合得到线性拟合的公式为
Pi′=-0.042 4+0.062 3i (13)
即Pi′=(0.019 9,0.082 2,0.144 5,0.206 8,0.269 1,0.331 4,0.393 7,0.456 0,0.518 3,0.580 6,0.642 9,0.705 2,0.767 5)。
(3) 根据P序列与Pi′的距离,以X(P)为基础,进行线性插值计算得
X(Pi′)=(17.5,18.1,18.7,19.2,19.7,20.2,20.4,
20.5,20.8,21.5,22.2,22.9, 23.6)
(4) 根据X(Pi′),分别建立GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型,得到三者的参数列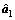 ,
,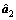 和
和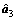 分别为:
分别为:
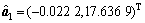
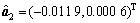
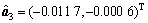
将以上参数代入各模型后求解得到各模型路基沉降的理论预测值,并进行误差比较及精度检验,计算结果如表8所示。
表5 路基最终沉降量
Table 5 Final settlement of road cm
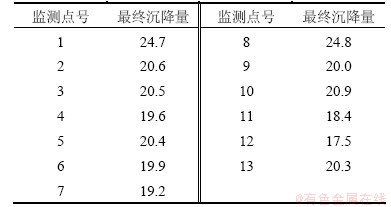
表6 指标因素灰色效果测度
Table 6 Index factors gray effect measure value
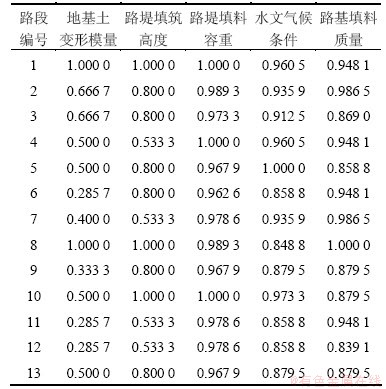
表7 各路段路基的靶心距
Table 7 Off-target distances of each roadbed section
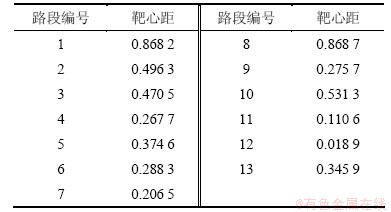
由表8可知:对于基于X(Pi′)的预测模型,GM(1,1)模型误差最小,精度也最高,因此,用GM(1,1) 来生成路基沉降因素靶心距与路基最终沉降之间规律。得到基于X(Pi′)的GM(1,1)预测模型为
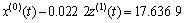
表8 各模型路基沉降误差检验结果
Table 8 Tested results of settlement error of each model
其时间响应序列为
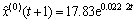
根据P序列利用最小二乘法进行拟合,得到线性拟合公式为
Pi′=-0.042 4+0.0623 i
求得
i=16.05 Pi′+0.68
式中:i即为t;r为路基沉降影响因素各靶心距,即为Pi′。
t=16.05 r+0.68
得到路基沉降影响因素靶心距与路基沉降之间的规律公式为
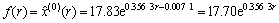 (14)
(14)
2.5 结果验证
非等距预测模型的原始数据序列即路基沉降影响因素的靶心距序列为
P=(0.018 9,0.110 6,0.206 5,0.267 7,0.275 7,
0.288 3,0.345 9,0.374 6,0.470 5,0.496 3,
0.531 3,0.868 2,0.868 7)
以P序列为基础,通过模型预测得到相应的路基最终沉降量序列为
X(P)=(17.5,18.4,19.2,19.6,20.0,19.9,
20.3,20.4,20.5,20.6,20.9,24.7,24.8)
将P序列代入式(14),得到相应的规律公式得到的路基最终沉降量为
f(P)=(17.8,18.4,19.1,19.5,19.5,19.6,20.0,
20.2,20.9,21.1,21.4,24.1,24.1)
对X(P)与f(P)进行误差检验,得到其平均相对误差为98.22%,后验比值c=0.1935,小误差概率p=100%,精度检验等级为一级。因此,由式(14)所得路基沉降影响因素靶心距在一定范围内,预测精度还是很高的,综合考虑P范围,可以认为在路基沉降影响因素靶心距值r∈[0.018 9,0.868 7]时,式(14)具有很高的预测精度。
3 结论
(1) 通过精度比较与模型优选,应用预测模型得出的结果比采用单一的预测方法更加科学合理、可靠;而改进灰靶决策理论通过灰色测度计算来生成效果向量,由于摆脱了人为主观因素的干扰,优于传统的灰靶决策理论中人为分级确定效果向量的方式,计算过程更加科学,生成的靶心距也更加能够体现了指标因素本身的特征。
(2) 利用改进灰靶决策理论与灰色预测模型对路基沉降规律分析,从路基本身的性质入手,对路基最终沉降量进行判定。该判定方式为道路路基施工工程实践中对路基最终沉降的预判提供了参考,有助于路基工程灾害的防治和路基沉降预防及治理成本的降低。
(3) 在将非等距的预测模型转化为等距的预测模型时,对于因变量X(Pi′)的生成采用的是比较常用的线性插值法,但是,其他生成方法如拉格朗日法可能会生成更加理想的X(Pi′)。
(4) 模型建立的以路基沉降影响因素靶心距作为自变量,以路基最终沉降量作为因变量的计算公式,经检验对背景工程路段是适用的,但该公式是否具有普适性、对于其他路段是否适用尚待考证,需要更多的数据与更多的工程实践进行检验。
参考文献:
[1] Chen S L, Gui M W, Yang M C, et al. Applicability of the principle of superposition in estimating ground surface settlement of twin-and-quadruple-tube tunnels[J]. Tunnelling and Underground Space Technology, 2012, 28: 135-149.
[2] WU Zhenzhi, YANG Guoxiang, LIN Jiaxiang, et al. Prediction and control of ground deformation and displacement due to large slurry shield tunneling using stochastic medium theory[C]//Advances and Experiences with Pipelines and Trenchless Technology for Water, Sewer, Gas, and Oil Applications. Shanghai, 2009: 1743-1754.
[3] 胡振南. 双曲线法在路基沉降预测中的应用研究[J]. 公路工程, 2011, 36(3): 145-148.
HU Zhennan. Study of the hyperbolic method in prediction of roadbed settlement[J]. Highway Engineering, 2011, 36(3): 145-148.
[4] 夏江, 严平, 庄一舟, 等. 基于遗传算法的软土地基沉降预测[J]. 岩土力学, 2004, 25(7): 1131-1135.
XIA Jiang, YAN Ping, ZHUANG Yizhou, et al. Predictions of soft ground settlements based on genetic algorithm[J]. Rock and Soil Mechanics, 2004, 25(7): 1131-1135.
[5] 吕培林, 周顺华. 软土地区盾构隧道下穿铁路干线引起的线路沉降规律分析[J]. 中国铁道科学, 2007, 28(2): 12-16.
LU Peilin, ZHOU Shunhua. Analysis on upper rail settlement in soft ground resulting from shield tunneling across main railway line[J]. China Railway Science, 2007, 28(2): 12-16.
[6] 曹文贵, 程晔, 赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究[J]. 岩土工程学报, 2005, 27(6): 621-625.
CAO Wengui, CHENG Ye, ZHAO Minghua. Studies on numerical manifold method for determination of safe thickness of karst roof in roadbed[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 621-625.
[7] 曹文贵, 颜艳芬, 张永杰. 基桩桩端岩溶顶板稳定性模糊能度可靠性分析方法[J]. 岩石力学与工程学报, 2009, 28(1): 88-94.
CAO Wengui, YAN Yanfen, ZHANG Yongjie. Fuzzy possibilistic reliability analysis method for stability of karst roof under pile tip[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 88-94.
[8] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2010: 95-105.
LIU Sifeng, GUO Tianbang, DANG Yaoguo, et al. The grey system theory and its application[M]. Beijing: Science Press, 1999: 95-105.
[9] Meysam Mousavi S, Jolai F, Tavakkoli-Moghaddam R, et al. A fuzzy grey model based on the compromise ranking for multi-criteria group decision making problems in manufacturing systems[J]. Journal of Intelligent & Fuzzy Systems, 2013, 24(4): 819-827.
[10] 王正新. GM(1,1)模型的特性与优化研究[D]. 南京: 南京航空航天大学经济与管理学院, 2007: 26-48.
WANG Zhengxin. Study on the characteristics and optimization of GM(1,1) model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Economics and Management, 2007: 26-48.
[11] Yao T X, Liu S F, Xie N M. Study on the properties of new information discrete GM (1,1) model[J]. J Syst Eng, 2010, 25(2): 164-170.
[12] 王正新, 党耀国, 杨虎. 改进的多目标灰靶决策方法[J]. 系统工程与电子技术, 2009, 31(11): 2634-2636.
WANG Zhengxin, DANG Yaoguo, YANG Hu. Improvements on decision method of grey target[J]. Systems Engineering and Electronics, 2009, 31(11): 2634-2636.
[13] 王鸿博. 应用于织机选型的灰靶决策[J]. 浙江工程学院学报, 2002, 19(4): 247-250.
WANG Hongbo. The grey target decision-making to choose weaving machine[J]. Journal of Zhejiang Institute of Science and Technology, 2002, 19(4): 247-250.
[14] 郭丽萍, 孙伟, 郑克仁, 等. 非等时距GM(1,1)直接模型及其在材料试验数据处理中的应用用[J]. 东南大学学报(自然科学版), 2004, 34(6): 39-41.
GUO Liping, SUN Wei, ZHENG Keren, et al. Non-equal interval GM(1,1) direct model and its application in processing of materials experimental data[J]. Journal of Southeast University (Natural Science Edition), 2004, 34(6): 39-41.
[15] 朱华吉, 马少娟. 非等时空距GM ( 1, 1) 模型在建筑物沉降预测中的应用[J]. 测绘工程, 2001, 10(4): 39-41.
ZHU Huaji, MA Shaojuan. Application of non- equal interval gray model to forecast of building subsidence[J]. Engineering of Surveying and Mapping, 2001, 10(4): 39-41.
[16] JIN Xiaoguang, ZENG Jie, LIU Xinrong, et al. Application of GM(1,1) optimized model in prediction of landslide[C]//Natural Computation (ICNC), 2007 International Conference on. Haikou, China, 2007: 735-739.
[17] 刘玉成. 改进的灰色Verhulst GM(1,1)建筑物沉降模型[J]. 中国地质灾害与防治学报, 2006, 17(4): 61-63.
LIU Yucheng. Improved gray like Verhulst GM(1,1) building subsidence model[J]. Journal of Geological Disasters and Prevention in China Quote, 2006, 17(4): 61-63.
[18] 单珂. 高速公路路基沉降影响因素的研究[J]. 内蒙古民族大学学报(自然科学版), 2012, 27(1): 37-40.
SHAN Ke. Highway Embankment settlement influencing factors[J]. Journal of Inner Mongolia University for Nationalities (Natural Science Edition), 2012, 27(1): 37-40.
(编辑 陈灿华)
收稿日期:2013-09-10;修回日期:2013-11-22
基金项目:国家自然科学基金资助(51308198);湖南省教育厅科学研究项目(12C0580);湖南省科技计划项目(2013GK3086)
通信作者:唐葭(1980-),女,湖南南县人,讲师,从事施工管理教学与研究;电话:18674806261;E-mail:340014557@qq.com