J. Cent. South Univ. (2017) 24: 2674-2684

DOI: https://doi.org/10.1007/s11771-017-3680-9

Restoring-force model of modified RAC columns with silica fume and hybrid fiber

YANG Tao(杨涛)¹, WANG She-liang(王社良)², LIU Wei(刘伟)^{2, 3}

1. School of Environmental and Chemical Engineering, Xi’an Polytechnic University, Xi’an 710048, China;

2. School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China;

3. Academy of Building Research of Shaanxi Provincial, Xi’an 710082, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017

Abstract: In order to establish a restoring-force model for modified concrete columns with recycled aggregates concrete (RAC), cyclic loading tests were carried out on five concretes with RAC columns and ordinary concrete frame columns under the combined influence with different admixtures and admixtures ratios (silica fume and hybrid fiber). The expressions for characteristic nodes of the skeleton curve were given by the analysis and numerical regression of the test results. In addition, the hysteretic rules of the restoring-force model and the expression for unloading stiffness were presented. Finally, we summed up the complete calculation method of the hysteretic restoring force, whose results were in good agreement with experiment. The results demonstrated that the proposed model could simulate and reflect the corresponding hysteretic behaviors, and the calculation method can provide the theoretical basis for the engineering application.

Key words: modified RAC columns; skeleton curve; unloading stiffness; hysteretic rule; restoring-force model

1 Introduction

The structural elastic plastic analysis can not only make up for the shortcomings of low precision and big errors in the traditional methods [1, 2], but also overcome the complexity and negative implementation of the dynamic time history analysis method, which has been a widely used method of seismic analysis for domestic and foreign scholars [3, 4]. In this process, the restoring force model is a practical mathematical model, and is based on a large number of experiments about the recovery force and deformation curve [5, 6]. Therefore, it is theoretically and practically significant to study the restoring force model.

In recent decades, a large number of construction wastes and a series of environment problems were produced by the large-scale modernization. For properly coordinating with the environmental pollution [7], arable land destruction and shortage of resources [8–10], RAC is the promising technology toward sustainability in the construction industry, which has been studied by domestic and foreign scholars. But almost all the results of researches proved that there are some defects such as high porosity, low aggregate strength and poor density in recycled aggregates [11]. In order to speed up the popularization and application of recycled concrete in practical engineering, it is necessary to improve the performance of the degradation and the mineral admixture is used most frequently [12]. Silica fume (SF), an ultrafine powder collected as a by-product of the silicon and ferrosilicon alloy production, consists of spherical particles with an average particle diameter of 150 nm. The most well-known effect of SF on concrete is the improvement on cement paste–aggregate interface. And SF also plays an important role in increasing of mechanical strengths of concrete because of having a pozzolanic activity, but the application of SF can cause concrete to have more brittle structure [13, 14]. Hybrid fiber (HF) includes the recycled steel fiber and nylon fiber, which were stripped from waste tires. HF has the reinforcement and toughness effect on RAC structures. For their easy access and low cost, silica fume and fiber have been widely used as mineral materials applied in the practical engineering [15, 16]. Previously the majority of the experimental studies investigated the effect of SF and HF on the basic mechanical properties of RAC, and the results showed that combination of SF and HF can effectively enhance the splitting tensile strength, flexural strength, ductility and crack resistance. However, there are few researches on the seismic performance of SF-and HF-reinforced concrete structures or structural members with RAC [17–19].

In this study, five RAC columns and one ordinary concrete column with different admixtures and admixtures ratios (silica fume and hybrid fiber) are performed to investigate the restoring-force model experimentally and theoretically. We compared the results of the analysis and experiment to establish the reasonable restoring force calculation model with modified recycled concrete, which could also provide a theoretical basis for its popularization and application.

2 Test survey

2.1 Design and fabrication of specimens

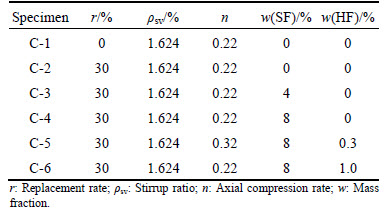
In this experiment, we designed six 1: 2-scaled rectangular columns with cross-section of 250 mm×250 mm and height of 1650 mm. The parameters include the fill-ins content, the axial compression ratio, and the stirrup ratios given in Table 1. All the rectangular columns are reinforced with 12 longitudinal reinforcement bars and reinforced transversely by stirrups. The typical reinforcement details for the specimens are shown in Fig. 1.

2.2 Material tests

In these tests 28 d cube compressive strength, the prism compressive strengths and elastic modulus of RCA have been tested, and the results are presented in Table 2. For all columns, steel bars were used, we tested the mechanical properties of the rebar used in this research, and the results are listed in Table 3. The basic properties of SF and HF are listed in Table 4 and Table 5, respectively.

Table 1 Design parameters of specimens

2.3 Testing devices and arrangement

All specimens were tested in the State Key Laboratory of Architecture, Science and Technology in West China at Xi’an University of Architecture & Technology under low cyclic lateral loads with vertical force. Horizontal load and vertical load were measured with the sensor connecting to the tension and compression jack. A constant vertical load of 276.4 kN was exerted on the top of a column by 1000 kN hydraulic jack. Then the 500 kN MTS electro-hydraulic servo actuator exerted low reversed cyclic horizontal load by the hydraulic servo load system as shown in Fig. 2.

According to the Building Seismic Test Method Procedure [20, 21], our test adopted the loading method of mixed force displacement, as shown in Fig. 3. The specimens adopted force to control load before its yield, and it employed displacement to control load after its yield. When the horizontal load dropped to 85% of the peak load, the test specimen reached final destruction [22].

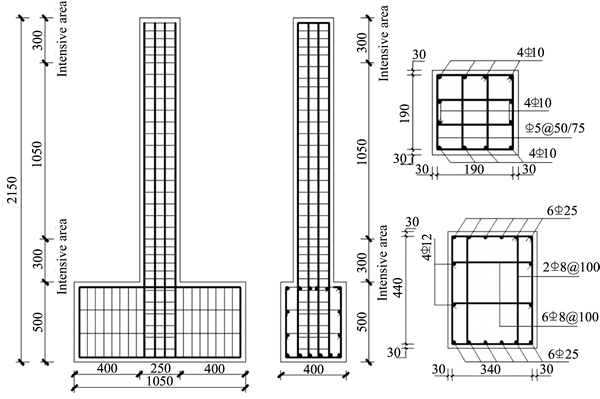
Fig. 1 Reinforcement details of specimens (Unit: mm)

Table 2 Mechanical properties of concrete

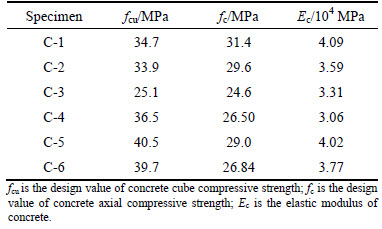
Table 3 Properties of steel and rebar

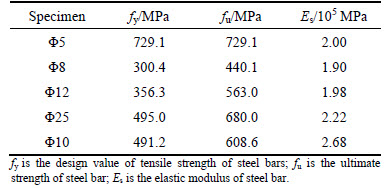
Table 4 Physical properties of silica fume (SF)

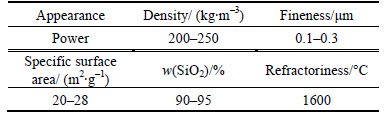
Table 5 Physical properties of hybrid fibers (HF)

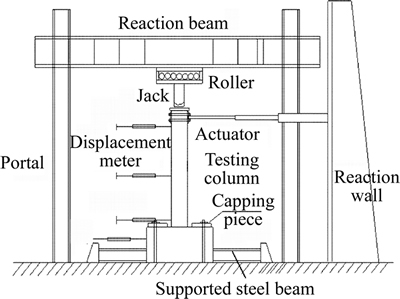
Fig. 2 Test set-up

Fig. 3 Loading procedure for tests:

3 Test results

3.1 General observations and failure patterns

In the stage of loading control, no cracks were observed in the specimens because the deformation of the columns was in the elastic range. When the lateral reached ±20 kN, the hair-like horizontal cracks were observed at the bottom of the columns. With the magnitudes of the lateral loads increasing, more and more horizontal cracks appeared in the columns, and some previous horizontal cracks gradually became longer and wider. Meanwhile, some diagonal cracks appeared at the bottom of the columns. As the loads continued to increase, the original diagonal cracks developed slowly, but the horizontal cracks developed rapidly and fused together gradually at the bottom of columns. When the lateral loads reached 70%–80% of the maximum lateral load, most of the specimens were already in the yield stage. The displacement- controlled cyclic loading was then applied, and no new horizontal and diagonal cracks were observed in the bottom, but the previous horizontal penetrated completely. When the loads reached to 2 times the yield displacement, more and more the diagonal cracks were found. With the increase of the cycles, the above-mentioned cracks propagated quickly and progressively. At the same time, the concrete cover around column bottom began to crush and peel off. After the specimens reached the maximum lateral load, the resisting force of the columns began to drop. With more and more concrete covering at the bottom of the columns peeling off and the yield of the longitudinal bars, the lateral loads on the specimens dropped rapidly, indicating the failure of specimens.

Compared to NAC column, we found that with the increase of the content percentage of SF and crack load, the cracks developed more slowly than NAC column. The reasons for this effect might be: 1) the character of micro silicon powder particle diameter, which can be filled between the cement particle pores, and further repair the initial damage of recycled aggregates; 2) the pozzolanic effect of micro silicon powder can induce secondary hydration reaction of cement hydrates, and improve the recycled concrete microstructure of gel content, which improves the bearing capacity of recycled concrete, and further delays the cracking and yielding of the specimens.

Comparing with the columns singly filled SF, although the cracks of the columns filled SF and HF appeared in a crisscross pattern, the width was smaller and the length was shorter than the rest of the specimen during the same period; also, in the bottom, we can observe the massive concrete of little particles, but macroscopic specimen failure pattern appears as “concrete crushed and not fall”. The addition of HF will improve the internal micro environment of the recycled concrete. The reasons for this effect might be: 1) the addition of HF leads to the effect of “fine ribs” in recycled concrete specimens, which plays the role of the tensile and the aggregate; 2) the addition of HF strengthened the continuity of the matrix, which eliminates and alleviates the emergence and development of micro cracks in the loading process; 3) the addition of HF weakened the stress concentration at the micro cracks, so that the stress field around the recycled concrete is more uniform; 4) the addition of HF reduced the accumulation of plastic deformation and damage of recycled concrete. Therefore, the improving of the bearing capacity and ductility lead to great improvement of the performance of recycled concrete frame columns. The specimens’ final failure characteristics are shown in Fig. 4.

3.2 Hysteresis loops

Figure 5 shows the hysteresis loops observed in the tests, which can be traced to the development of lateral displacement on the top of all frames under the cyclic loading. Based on Fig. 5 the following observations can be noted: Clearly, all specimens’ hysteresis curves show inconspicuous differences, and the spindle-shaped loops indicate the good energy dissipation capacity of all the columns. At the stage of no cracking or just before cracking, these curves are approximately straight lines,which indicate that the specimens are in an elastic state. Within each cycle, the decrease of the secant stiffness caused by the cyclic loading is somewhat insignificant. The residual displacement is small when unloading occurs, which leads to the energy dissipation, which is defined as the area on which a hysteresis loop covers and is also being small. When the specimens step into an elastic-plastic stage, as cracks appear at the foot of the specimens, the slopes of the hysteresis loops begin to decrease, and a larger residual deformation is observed when the lateral load is removed. In the displacement- controlled stage, the hysteresis curves of the columns become larger and wider as the displacements become larger. With respect to the loading process at each displacement level, both strengths and stiffness of the specimens decrease as the number of displacement cycles increases, which mainly reflects the damage accumulation in the specimens.

Fig. 4 Failure patterns of specimens:

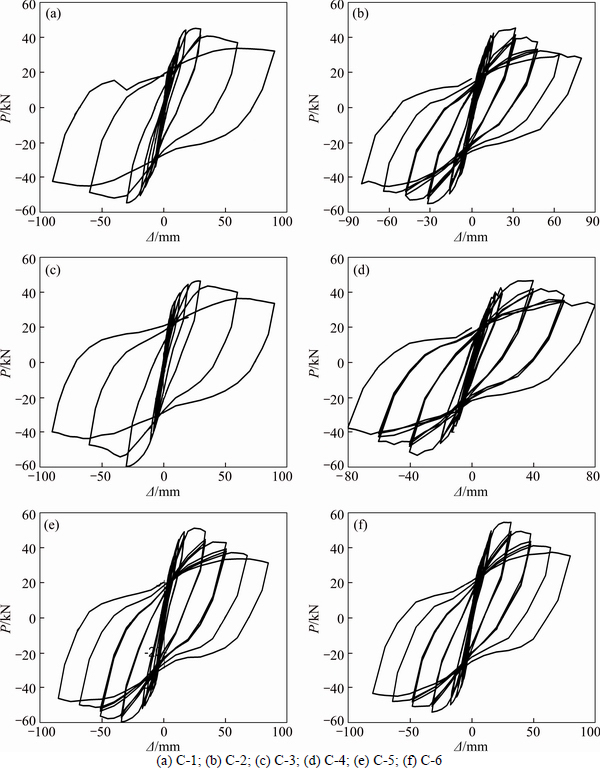
Fig. 5 Hysteresis loops of specimens:

3.3 Skeleton curves

The skeleton curves indicate the relationship between the top-loads and corresponding displacements from the hysteresis loops of the specimens, as shown in Fig. 6. From the skeleton curves, the cracking loading point, the yield loading point, the maximum loading point, as well as the ultimate loading point can be easily recognized, which can be divided from the loading process into the elastic, the elastic–plastic and the failure phases. Most of the skeleton curves show the resistance of the specimens loading decreasing slowly, which indicates that the investigated columns have good ductility.

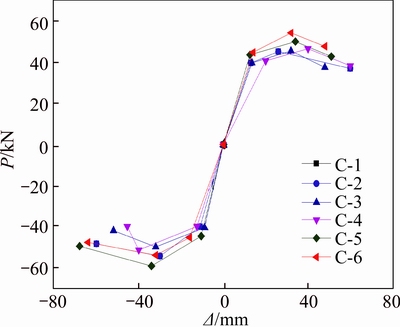
Fig. 6 Load–displacement skeleton curves

The skeleton curves of all specimens overlap before the yield load point of the column, which indicates that the initial stiffness of the columns is similar; it shows that the SF content has little influence on the initial stiffness. After the yield load point, the skeleton curves exhibit some differences in the elastic–plastic and failure phases. The SF content has some impact on the bearing capacity and ductility of the specimens, but is not very obvious. So as the influence of the HF content on the initial stiffness, it was indicated by the overlapped skeleton curves before the yield load point of the column. After the yield load point，the skeleton curves become different from the elastic–plastic and failure phases. With the increasing of the HF content, the yield load, peak load and bearing capacity improve obviously and the stiffness decreases slowly, which reflects that the specimens filled with SF and HF together can obviously improve the seismic performance of RAC columns.

The characteristics of load and displacement are shown in Table 6. In this table, P_y, P_m, P_u are respectively on behalf of the yield load, ultimate load and ultimate failure load, while △_y, △_m, △_u belong to the corresponding displacements.

4 Restoring-force model

Under low cyclic loading, the structural stiffness of reinforced concrete will be reduced due to the cracking of concrete, Bauschinger effect, slip caused by the bond between reinforcement and concrete, which would inevitably lead to the change of load–displacement skeleton curve. Therefore, for determining the stiffness variation of the characteristic points of the skeleton curve, it is necessary to ascertain the load displacement curve.

4.1 Skeleton curve

In fact, the characteristic curve is very complex in the elastic–plastic analysis. Therefore, the fold lines are widely used, including bi-linear model [23], Clough model [24], three broken line model [25] and four broken line model [26]. By the testing hysteretic curve and skeleton curve, it can be seen that no significant changes of the stiffness have occurred. In this work, we adopted three broken line model for the theoretical analysis of restoring force. The model is shown in Fig. 7.

As shown in the picture, three points (A, B, C) represent the specimen yield point, peak point and failure point, respectively. The numerical experiments are shown in Table 6 and the test section stiffness analysis is listed as follows.

1) Preyield stiffness

By the above analysis, it can be considered that the stiffness of the specimen before yield is equal to the crack stiffness. In other words, it is assumed that this stage is still in the elastic one. At this point, we can obtain the equation by the knowledge of structure mechanics:

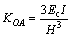                                 (1)

The above formula can be obtained from the knowledge of material mechanics, and E_c is the elastic modulus of the modified recycled concrete. Due to the small reinforcement areas and volume ratio, the inertia moment of this part is assumed to remedy the loss caused by the concrete cracking without the consideration of the conversion section area of the reinforcement. Approximately put the whole section as the base of calculating the inertia moment.

2) Yield load P_y and yield displacement △_y

From Table 6, the ratio between the yield load P_y and the ultimate load P_m is between 0.83–0.88, and the approximate ratio is 0.85. At this time Δ_y can be derived as

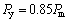
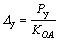                                  (2)

3) Ultimate load P_m

According to the test results, the amount of silica powder and fiber both affect the ultimate load P_m, which varies with the amount of silica powder and fiber. The formula of the ultimate bending moment is calculated as follows [27]:

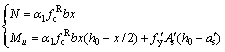         (3)

where μ is the specimen axial compression ratio, which is taken 0.22; is the axis compressive strength. By the above, we can calculate the general formula of ultimate bending moment, and then consider the effect of silica powder and fiber. The influence of silica fume can be ignored on P_m from the test results, only considering the fiber. The ultimate load P_m can be calculated by the least square fitting:

             (4)

where H is height of specimen to improve the accuracy with the small amount of fiber, then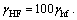

Table 6 Experimental results of characteristic values

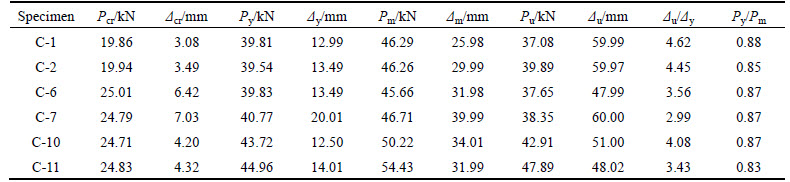
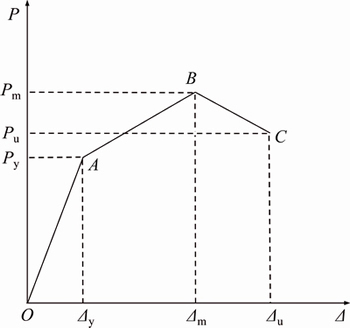
Fig. 7 Skeleton curve model

4) Ultimate displacement △_m

There are many factors influencing the ultimate displacement, such as pouring quality, bond slip between the steel bar and concrete, accuracy of the data record, length of plastic hinge.

Considering the comprehensive effects of fiber and silica fume, we can describe the curve by means of one equation from the test:

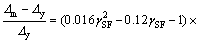
                   (5)

where γ_SF=100γ_sf, γ_HF=100γ_hf.

5) Stiffness of reinforcement stage K_AB

By the above analysis, the stiffness of this stage can be obtained:

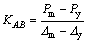                              (6)

6) Ultimate failure load P_u and ultimate failure displacement △_u

In accordance with the relevant regulations and the actual value of test process, P_u can be expressed as P_u=0.85P_m.

It can be concluded from table 6 that silica fume and fiber have great influence on ductility coefficient (△_u/△_y). In order to ensure the accuracy of the results of theoretical calculation, it takes SF and HF into consideration together, and then it is determined as follows:

          (7)

7) Stiffness of descending branch K_BC

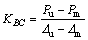                              (8)

According to the test results, the positive and negative loadings of characteristic values have few differences, which are assumed to have the same stiffness at corresponding stage. The results are shown in Fig. 8.

4.2 Hysteretic curve

According to the P–△ rules of the ordinary concrete column as shown in Fig. 9 [28, 29], the numbers from small to large in figures show the orderliness under the normal and reverse loading. In order to facilitate the expression, the path of two points (M, N) is indicated as L_m-n, and its hysteretic rules are summarized as follows:

1) Rule of bi-directional loading pre yield (L_0–1 and L_0–4)

When the restoring force still does not reach the yield load (points 1, 4), the component can be considered the elastic stage approximately. In this stage, the residual deformation and stiffness degradation are left out of account. In other words, the stiffness keeps constant and the bi-directional loading is carried out according to the skeleton curve as follows:

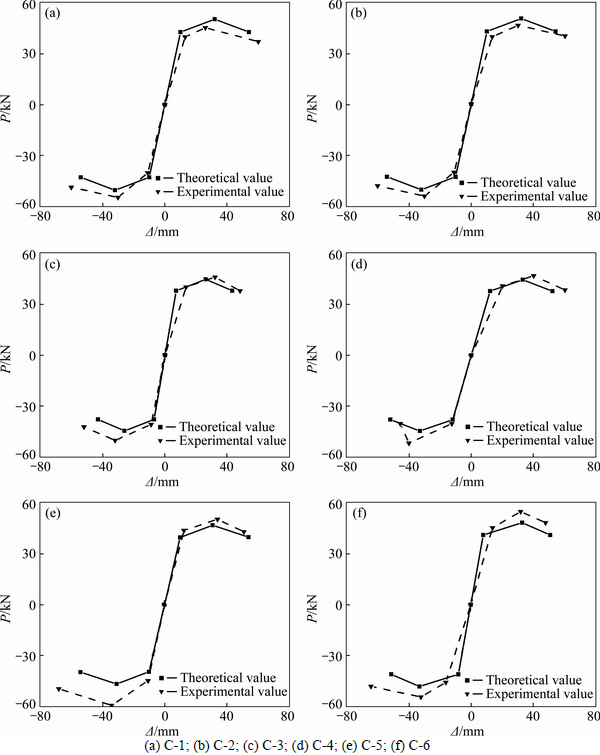
Fig. 8 Calculated skeleton loops and experimental skeleton loops:

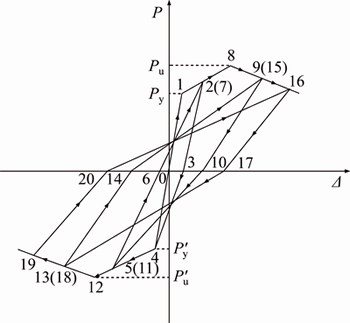
Fig. 9 Hysteretic rule

2) Rule of bi-directional loading after yield (L_2–3 and L_5–6)

When the restoring force exceeds the yield bearing capacity (P_y), but not yet reaches the ultimate bearing capacity (P_u), K_AB is taken approximately as the loading stiffness. While taking the reduction initial stiffness 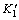as the unloading stiffness, it can be calculated by Eq.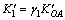(9).

                                 (9)

The stiffness reduction factor for this stage of the formula is determined by the following method. 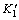is equal to the slope between the relative stress point starting to unload and the zero load point of this loop. Figure 10 shows a schematic diagram of hysteresis loop where the points A, C are for the hysteresis loop of forward and reverses loading and unloading point, while B, D are the corresponding points of the zero displacement.

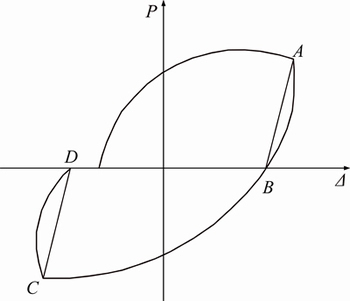
Fig. 10 Unloading stiffness diagram

The unloading stiffness after yield does not change with the cycle numbers; however, with the increase of applied displacement, it is gradually becoming smaller. Therefore, the regression analysis of the unloading stiffness of the test is carried out according to the statistical analysis of the test column, as shown in Fig. 11.

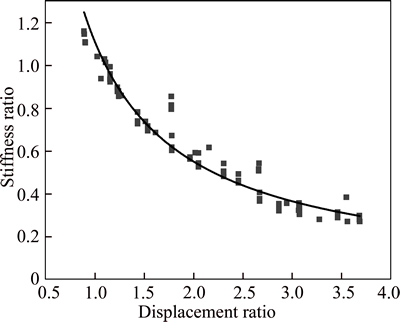
Fig. 11 Relation of unloading stiffness and displacement ratio

The stiffness value of this stage can be obtained as follows:

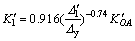                      (10)

where and 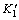equal the corresponding unloading displacement and stiffness in the same stage and can be calculated by

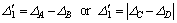
3) Rule of bi-directional loading after limit (L_8–9 and L_12–13)

When the recovery force exceeds the limit level, the load stiffness is calculated:

                                (12)

4) Reverse loading and forward loading rule (L_3–4, L_10–11 and L_6–7)

In Ref. [30], the maximum displacement of the reverse does not reach P_y after unloading. At this point, the reverse loading path is pointed from 0 to 4. When the reverse maximum displacement exceeds P_y, the path has experienced from 0 to the maximum displacement point. When the reverse is unloaded, the maximum displacement point is directly from P=0 to the positive experience.

Using the above recovery force hysteresis rule, the theoretical results of the 6 test columns are carried out respectively, and we compared the results with the experiment, as shown in Fig. 12.

The analysis results show that the analysis method can simulate the actual seismic performance with relatively enough accuracy. In other words, it is able to provide the necessary theoretical basis for the application in the project.

5 Conclusions

Through the analysis of experimental data, the restoring-force model of modified RAC columns with silica fume and hybrid fiber is discussed and the conclusions can be made as follows:

1) Compared with C1 and NAC column, the SF and HF combination reinforced RAC columns behave similarly in the aspect of their failure patterns under low cyclic loads, but the width and length of cracks in the latter are smaller and shorter. Moreover, the HF reinforced columns in the final failure stage show the phenomenon of “concrete crushed and not fall”.

2) The hysteresis loops and skeleton curves of the columns suggest that the seismic performance of RAC columns is comparable to that of conventional concrete. Appropriate application of the SF and HF can effectively improve the seismic performance of RAC columns.

3) Based on the experimental skeleton curves of six columns with different content SF and HF, each feature point computational formula can be proposed by numerical regression method, and theoretical calculation results are in good agreement with the experiment. In addition, by the theory analysis with the segments of hysteresis curve, statistical regression formula unloading section stiffness is presented, and then the hysteretic rule of the complete hysteretic curve restoring-force model can be obtained.

4) Compared with the test, the results obtained by the proposed hysteretic model are nearly same. It is demonstrated that this model can simulate the seismic behavior, and can provide the theoretical basis for the engineering application.

Fig. 12 Skeleton curve of theoretical value and experimental value:

References

[1] WORDEN K, TOMLINSON G R. Nonlinearity in structural dynamics: Detection, dentification and modeling [M]. Bristol, UK: Institute of Phsysics Publishing, 2001.

[2] YE Kang-sheng, WU Ke-wei. Elasto-plastic large displacement analysis of spatial skeletal structures [J]. Engineering Mechanics, 2013, 30(11): 1–8. DOI:10.6052/j.issn.1000-4750.2012.06.0436.

[3] KERSCHEN G, WORDEN K, VAKAKIS A F, GOLINVAL J C. Past, present and future of nonlinear system identification in structural dynamics [J]. Mechanical Systems and Signal Processing, 2007, 20(3): 505–592. DOI: 10.1016/j.ymssp.2005.04.008.

[4] YIN Hua-wei, WANG Meng-fu, ZHOU Xi-yuan. Studies and improvements on structural static pushover analysis method [J]. Engineering Mechanics, 2003, 20(4): 45–49. (in Chinese)

[5] GUO Zi-xiong, YANG Yong. State-of-the-art of restoring force models for RC structures [J]. World Earthquake Engineering, 2004, 20(4): 47–51. (in Chinese)

[6] JUN Zhao, DUN Hua-hua. A restoring-force model for steel fiber reinforced concrete shear walls [J]. Engineering Structures, 2014, 75: 469–476. DOI:10.1016/j.engstruct.2014.06.013.

[7] ZHANG Bo, WANG She-liang. Influence of crush value index on compressive strength of recycled aggregate concrete [J]. Industrial construction, 2013, 43(11): 1–6. (in Chinese)

[8] ZHOU Hong-min, CHAI Jun, CHAI Hua. Introduction of recycled aggregate concrete technology and current research situation [J]. Concrete, 2008(12): 75–76. (in Chinese)

[9] BRANGT A M. Fiber reinforced cement-based (FRC) composites after over 40 years of development in building and civil engineering [J]. Composite Structures, 2008, 86(1–3): 3–9. DOI:10.1016/ j.compstruct.2008.03.2006.

[10] XIAO Jian-zhuang, WANG Chang-chun, DING Tao. Study and evaluation on the seismic performance of recycled aggregate concrete frame [J]. China Civil Engineering Journal, 2013, 43(8): 55–66. (in Chinese)

[11] SUMAIYA B H, M SHAHRIA A. Mechanical behavior of three generations of 100% repeated recycled coarse aggregate concrete [J]. Construction and Building Materials, 2014, 65(29): 574–582. DOI:10.1016/j.conbuildmat.2014.05.010.

[12] WANG She-liang, YU Yang, ZHANG Bo. Experimental study on influence of mechanic properties of recycled concrete by fly ash and silica fume [J]. Concrete, 2011(12): 53–55. (in Chinese)

[13] SHANNAG M J. High strength concrete containing natural pozzolan and silica fume [J]. Cement & Concrete Composites, 2000, 22(6): 399–406. DOI:10.1016/S0958-9465(00)00037-8.

[14] ATIS C D, OZCAN F, KILIC A, KARAHAN O, BILIM C, SEVERCAN M H. Influence of dry and wet curing conditions on compressive strength of silica fume concrete [J]. Building and Environment, 2005, 40(12): 1678–1683. DOI: 10.1016/ j.buildenv.2004.12.005.

[15] WEI Cui-mei, XU Li-hua, HUANG Le. Experimental study on restoring force models for steel-polypropylene hybrid fiber reinforced concrete columns [J]. China Civil Engineering Journal, 2014, 47(2): 227–234. (in Chinese)

[16] YU Yu-zhen, DENG Li-jun, SUN Xun. Centrifuge modeling of dynamic behavior of pile-reinforced slopes during earthquakes [J]. Journal of Central South University, 2010, 17(5): 1070-1078. DOI: 10.1007/s11771-010-0599-9.

[17] M. Properties of polypropylene fiber reinforced concrete using recycled aggregates [J]. Construction and Building Materials, 2015, 98: 620–630. DOI:10.1016/ j.conbuildmat.2015.08.133.

[18] XIE Jian-he, GUO Yong-chang LIU Li-sha. Compressive and flexural behaviors of a new steel-fiber-reinforced recycled aggregate concrete with crumb rubber [J]. Construction and Building Materials, 2015, 79: 263–272. DOI: 10.1016/j.conbuildmat.2015.01.036.

[19] ZHU Hai-tang, GAO Dan-ying, WANG Zhan-qiao. Experimental study on fracture properties of hybrid fiber reinforced high-strength concrete [J]. Journal of Building Structures, 2010, 31(1): 41–46. (in Chinese)

[20] GB 50152–1992. Standard methods for testing of concrete structures [S]. (in Chinese)

[21] JGJ 101–96. Specification of testing methods for earthquake resistant building [S]. 1997. (in Chinese)

[22] GUO Zhen-hai, SHI Xu-dong. Reinforced concrete theory and analysis [M]. Beijing: Tsinghua University Press, 2003. (in Chinese)

[23] PENIZEN J. Dynamic response of elastic-plastic frames [J]. Journal of Structural Division, ASCE, 1962, 88(ST7): 1322–1340.

[24] CLOUGH R W, JOHNSTON S B. Effect of stiffness degradation on earthquake ductility requirements [C]// Proceedings of the 2nd Japan Earthquak Engineering Symposium. Tokyo: JSCE, 1966: 37–44.

[25] TAKEDA T, SOZEN M A, NIELSON N N. Reinforced concrete response to simulated earthquakes [J]. Journal of Structural Division, ASCE, 1970, 96(ST12): 2557–2572. DOI:10.1017/ CBO9781107415324.004.

[26] ZHU Bo-long, ZHANG Kun-lian. A study of restoring force characteristics of reinforced concrete flexural members with a constant axial load [J]. Journal of Tongji University, 1981, 9(2): 1–10. (in Chinese)

[27] LIANG Xing-wen, WANG She-liang, LI Xiao-wen. Design principle of concrete structure [M]. Beijing: Science Press, 2007. (in Chinese)

[28] PARK Y, ANG A H. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering，1985, 111(4): 722–739. DOI: 10.1061/(ASCE)0733-9445(1985)111: 4(722).

[29] QI Yue, ZHENG Wen-zhong. Restoring-force model of load versus displacement for concrete columns with high strength core [J]. Journal of Harbin Institute of Technology, 2010, 42(4): 531–535. (in Chinese)

[30] KANG J W, LEE J. A new damage index for seismic fragility analysis of reinforced concrete columns [J]. Structural engineering and mechanics, 2016, 60: 875–890. DOI: 10.12989/sem.2016.60.5. 875.

(Edited by YANG Hua)

Cite this article as: YANG Tao, WANG She-liang, LIU Wei. Restoring-force model of modified RAC columns with silica fume and hybrid fiber [J]. Journal of Central South University, 2017, 24(11): 2674–2684. DOI:https://doi.org/10.1007/s11771-017-3680-9.

Foundation item: Project(51178388) supported by the National Natural Science Foundation of China; Project(2013SZS01-Z02) supported by Key Laboratory Fund of Shaanxi Province, China

Received date: 2015-11-20; Accepted date: 2017-11-06

Corresponding author: YANG Tao, Lecturer, PhD; Tel:＋86–18092916886; E-mail: yangtao@xpu.edu.cn