DOI: 10.11817/j.issn.1672-7207.2016.04.008
双足步行机器人在线步态生成与偏航控制策略
丁加涛,肖晓晖,王杨
(武汉大学 动力与机械学院,湖北 武汉,430072)
摘要:针对双足步行机器人的偏航行走需求,提出一种步态生成与偏航行走控制策略,实现步态模式的在线生成与自主偏航行走。其步骤为:首先,基于零力矩点(ZMP)稳定判据,采用线性倒立摆模型和正-逆运动学循环求解算法,建立离线步态生成器;其次,采用预观控制理论,建立用于轨迹跟踪的预观控制器,实现双足步态的在线生成;然后,引入角度系数,运用矢量合成法,根据目标偏航角度,通过回放-纠正方法确定合适的固定系数;最后,采用MATLAB和Adams组成的联合仿真平台,验证方法的有效性。研究结果表明:该方法能利用离线生成的角度,有效减少质心侧向轨迹跟踪误差;通过矢量合成和回放纠正,选取合适的角度系数,实现无偏航步态的在线生成;不需要实时规划参考ZMP轨迹,在保证稳定的前提下,实现15°和30°偏航行走。
关键词:双足步行机器人;步态生成;偏航控制;矢量合成;回放-纠正
中图分类号:TP242 文献标志码:A 文章编号:1672-7207(2016)04-1136-08
Strategy for biped gait robot online generation and yaw control
DING Jiatao, XIAO Xiaohui, WANG Yang
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: To meet the task requirements of autonomous yaw for biped robot, a combination strategy for biped gait robot generation and yaw control was proposed, thus the online biped gait generation was realized and the autonomous yaw was obtained. The procedures were as follows. Firstly, based on the zero moment point (ZMP) stabilization criterion, using the linear inverted pendulum model and forward-inverse kinematics cyclic solution algorithm, the offline biped gait generator was built. Secondly, adopting the preview control theory, the online generator was established to realize real-time generation and ZMP trajectory tracking. Then, combining the two generators, the concept of angle coefficient was proposed. After that, the method of displacement vector synthesis was adopted. Through the playback-correction scheme, the angle coefficient was acquired to satisfy the purposed yaw angle. Finally, the effectiveness was verified on the co-simulation platform using the MATLAB and Adams softwares. The results show that the proposed method is effective to utilize the offline generated angle and reduce the tracking error of the center of mass (COM) lateral trajectory. Through vector synthesis and playback-correction, the suitable angle coefficient can be achieved and no-yaw walking pattern can be obtained. Without requiring real-time ZMP trajectory design, stable biped gait with 15°and 30° yaw is realized.
Key words: bipedal walking robot; walking pattern generation; yaw control; vector synthesis; playback-correction
双足步行机器人具有高度的活性、适应性和与人的亲和力,在生产服务、医疗康复等方面有着广阔的应用前景[1]。步态模式生成和自主偏航控制是实现双足灵活运动关键。双足步态生成策略可分为离线生成和在线生成2类。1972年,VUKOBRATOVIC等[1-2]提出零力矩点(zero moment point,ZMP)概念并给出了相应的步行稳定性判据。基于此,HUANG等[3]通过规划足部轨迹和髋关节轨迹,离线获得了高稳定裕度的平稳步态。KAGAMI等[4]研究动态平衡条件下ZMP与质心的关心,实现了步态的离线快速生成。但是,离线步态生成策略未能考虑环境的多变性,适应性不强。为了增强适应性,研究者提出了多种控制策略。MITOBE等[5]提出角动量控制法来协调机器人整体姿态;KOMURA等[6]提出1种反馈控制器来抵消行走过程的冲击。但是,一方面,仅仅使用一种在线控制策略也很难获得较高的适应性,有时需要多种控制方式协调进行[7]。另一方面,这些控制策略往往依赖于离线规划的步态,效果受到限制。因此,越来越多的研究者将注意力转向在线步态生成。HARADA等[8]提出数值求解法,实现了步态的实时生成。KAJITA等[9]使用预观控制器进行在线步态跟踪,生成了用于螺旋阶梯行走的步态。DIEDAM等[10]使用模型预测控制器实现足部位置自适应调整。由于具有良好的跟踪性,预观控制在步态在线生成与步行控制方面得到了广泛的运用[11-12]。偏航行走有直线跟踪行走和主动偏航行走2种需求。一方面,为了提高步行速度,在环境条件允许时需要避免偏航。 HIRABAYASHI等[13]通过调整摆动腿轨迹减少了偏航力矩;CISNEROS等[14]利用机器人不工作的自由度对步行姿态进行补偿,减少了偏航位移。另一方面,在某些环境和特殊任务要求下(避障等),应该采取主动偏航行走策略。STROM等[15]利用预观控制器,通过4个子工作框架的信息交换,实现了机器人的偏航与换向。YEON等[16]利用机器人在单足相期间产生的偏航,实现了快速的偏转。但以上2类策略将实现无偏航直线行走和主动偏航区分考虑,难以满足实际任务需求。TZUU-HSENG等[17]以拉格朗日插值法为基础,编制了步态数据库,结合强化梯度学习和模糊逻辑控制方法,实现了对曲线轨迹的跟踪,但编制步态数据库需要大量时间。KAGAMI等[18]提出基于视觉系统的回放方法,用于汽车行驶时跟踪弯曲路径。 等[19]将回放法与错误纠正相结合,实现了双足步行机器人对人体步行数据的学习。基于此,本文作者针对双足步行机器人下肢结构,提出一种在线步态生成和偏航控制策略。在步态生成方面,采用ZMP 稳定判据,利用时域离散法,通过正-逆运动学的循环求解离线获得一组步态角度。利用预观控制理论构造预观控制器,将离线生成的关节角度作为在线逆运动学求解的初始角度,实现步态模式的在线生成与输出。在偏航控制方面,将离线生成的角度和在线生成的角度作为偏航控制算法的2组输入量;引入角度系数,将这2组角度结合起来。利用矢量合成的平行四边形法则确定目标轨迹需要的模糊角度系数;通过回放-纠正法确定准确的系数,以实现满足目标偏航角度的步态模式的实时生成。
等[19]将回放法与错误纠正相结合,实现了双足步行机器人对人体步行数据的学习。基于此,本文作者针对双足步行机器人下肢结构,提出一种在线步态生成和偏航控制策略。在步态生成方面,采用ZMP 稳定判据,利用时域离散法,通过正-逆运动学的循环求解离线获得一组步态角度。利用预观控制理论构造预观控制器,将离线生成的关节角度作为在线逆运动学求解的初始角度,实现步态模式的在线生成与输出。在偏航控制方面,将离线生成的角度和在线生成的角度作为偏航控制算法的2组输入量;引入角度系数,将这2组角度结合起来。利用矢量合成的平行四边形法则确定目标轨迹需要的模糊角度系数;通过回放-纠正法确定准确的系数,以实现满足目标偏航角度的步态模式的实时生成。
1 步态生成
首先研究离线步态生成的基本理论,然后实现步态模式的在线生成。
1.1 离线步态生成
以ZMP稳定判据作为依据,规划出合适的ZMP(zero-moment point)轨迹和足部运动轨迹,通过逆运动学计算生成步态模式。
1.1.1 ZMP 稳定判据
ZMP是指机器人在重力和惯性力的作用下,地面反力的倾覆力矩等于0 N·m的点。ZMP稳定判据指出:双足步行机器人实现稳定行走的前提是ZMP应该位于足部支撑多边形的内部[1]。本文采用此稳定判据,指导ZMP轨迹和足部轨迹的离线规划。ZMP轨迹和足部轨迹示意图如图1所示,其中,x轴指向前进方向,y轴指向侧行方向,规划的参考ZMP轨迹始终位于足部支撑多边形(图(1)中虚点线与足部围成的区域)的内部。
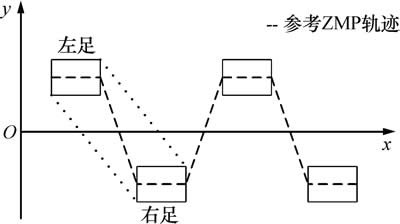
图1 ZMP轨迹和足部轨迹示意图
Fig. 1 Diagram of ZMP trajectory and foot trajectory
1.1.2 线性倒立摆模型
采用线性倒立摆模型。该模型假定机器人腿部无质量;将机器人简化成1个质量集中于腰部的倒立摆。根据该模型,得ZMP和质心位置的关系式[9]:
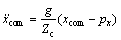 (1)
(1)
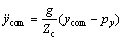 (2)
(2)
式中:Zc为模型质心高度;xcom和ycom分别为质心前向、侧向位移;px和 py分别为质心ZMP前向、侧向位移;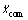 ,
, 和g分别为质心前向加速度、侧向加速度以及重力加速度。本文预先规划ZMP轨迹,再求解质心轨迹,采用桌子-小车模型[9],将双足步行机器人近似为1个不计质量的桌子及在其上水平运动的小车。得ZMP和质心关系式:
和g分别为质心前向加速度、侧向加速度以及重力加速度。本文预先规划ZMP轨迹,再求解质心轨迹,采用桌子-小车模型[9],将双足步行机器人近似为1个不计质量的桌子及在其上水平运动的小车。得ZMP和质心关系式:
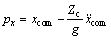 (3)
(3)
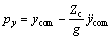 (4)
(4)
1.1.3 离线步态求解流程
离线步态生成算法流程如图2所示,流程如下。
1) 规划ZMP轨迹,求解对应的质心和足部运动轨迹。
2) 利用杆式模型,将质心位姿信息和足部位姿信息分别赋给腰部杆和足部杆。
3) 从运动链首端(腰部杆)到运动链末端(足部杆)进行正-逆运动学循环计算,得到机器人10个关节的角度-时间序列即步态模式。
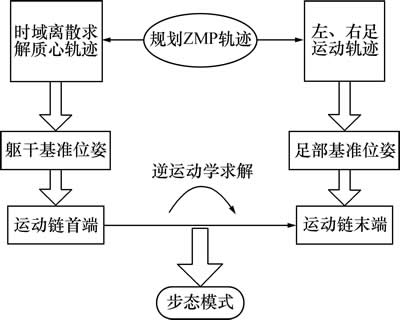
图2 离线步态求解流程
Fig. 2 Calculation proceedings of offline biped gait generation
1.2 预观控制理论
利用未来的信息进行控制的方法叫预观控制[9, 20]。由于使用未来一段时间的步态信息预观控制器对目标轨迹具有良好的跟踪性,本文采用预观控制器作为在线步态发生器。将式(3)和(4)统一为
 (5)
(5)
其中:p和x分别代表ZMP和质心轨迹; 代表质心的加速度。式(5)反映了式(3)和(4)中的前向和侧向的关系。为了便于使用现代控制理论处理桌子-小车模型,选取质心加速度的变化率
代表质心的加速度。式(5)反映了式(3)和(4)中的前向和侧向的关系。为了便于使用现代控制理论处理桌子-小车模型,选取质心加速度的变化率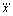 作为系统的控制输入,即
作为系统的控制输入,即
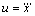 (6)
(6)
以此为输入,由式(5)得状态方程:
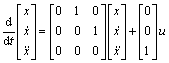 (7)
(7)
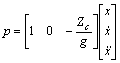 (8)
(8)
以采样时间Dt对连续系统方程(7)和(8)进行离散化处理:
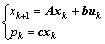 (9)
(9)
其中: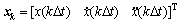 ;
;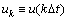 ;
; ;
;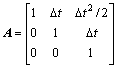 ;
; ;
; 。
。
为了减小跟踪误差,采用增量形式:
 (10)
(10)
其中: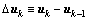 ;
;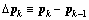 ;
;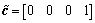 ;
;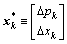 ;
;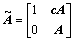 ;
;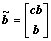 。
。
以上是一个最优跟踪问题。为了使系统的输出pk尽可能精确地跟踪目标ZMP(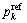 ),并且能够实现过程控制,采用积分型性能指标J:
),并且能够实现过程控制,采用积分型性能指标J:
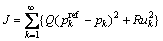 (11)
(11)
为了极小化J,据现代控制论和预观控制理论,确定控制输入的表达式:
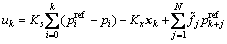 (12)
(12)
控制增益 Ks和Kx,预观增益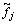 和跟踪步长N由预观控制理论计算,Q和R为正的权系数。
和跟踪步长N由预观控制理论计算,Q和R为正的权系数。
在线步态求解流程见图3。未来目标ZMP值储存于FIFO寄存器,其输出值作为当前的参考值。预观控制器用FIFO缓冲器中的ZMP参考值和小车的状态计算控制输入。其中,小车状态包括质心位移和速度,可根据桌子-小车模式生成。
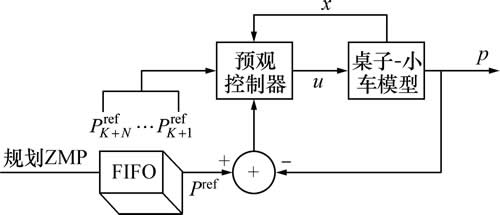
图3 基于预观控制的在线步态求解流程
Fig. 3 Calculation proceeding of online biped gait generation based on preview control
2 偏航控制
2.1 偏航与角度系数
机器人在行走过程中,摆动腿的加速和减速产生了绕支撑腿的偏航力矩。若偏航力矩大于地面对支撑脚的摩擦力矩,则会发生偏转[13]。机器人偏航反映在位姿上就是质心(center of mass,COM)轨迹(侧前-侧向位移轨迹,y-x曲线)实现偏航与转向。不考虑质心高度变化,可利用质心轨迹在水平面上的投影研究机器人的偏航(简称质心轨迹)。
离线步态生成算法只能生成稳定行走的步态。要使机器人产生特定角度的偏航,则需事先规划好相应的ZMP轨迹。但一方面,离线规划ZMP轨迹容易导致转弯处的关节角突变,从而使机器人失稳;另一方面,由于没有在线调整策略,不能保证规划ZMP的跟踪效果。预观控制强调跟踪规划的ZMP 轨迹,但难以确定合适的权重系数Q,R和跟踪步长N。在仿真中发现,离线生成的轨迹和预观控制在线生成的轨迹往往是不重合的2条曲线。经分析知,这种方向的不同是离线生成的角度-时间序列和在线生成的角 度-时间序列不同所致。由机器人正运动学理论,一组角度-时间序列对应于1条运动轨迹即1条质心轨迹。采用拉格朗日插值法,引入角度系数(Kwei),利用离线计算的角度(θofflne)和在线生成的角度(θonlne),得到计算式:
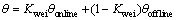 (13)
(13)
为了生成目标偏航角度的质心轨迹,只需要确定合适的角度系数即可。
2.2 矢量合成法确定目标角度系数模糊值
规划的ZMP轨迹是与前进方向夹角为0°的直线,在理想情况下,相应的质心轨迹与前进方向夹角也应为0°,但实际上并非如此。本文将离线和在线生成的轨迹近似为与前进方向呈一定夹角的直线。记离线生成的轨迹方向矢量记为V1,预观控制生成的轨迹方向矢量记为V2,目标偏航轨迹方向矢量记为V。在笛卡尔坐标系中,由V1,V2合成V的关系可以由平行四边形法则确定,如图4所示。
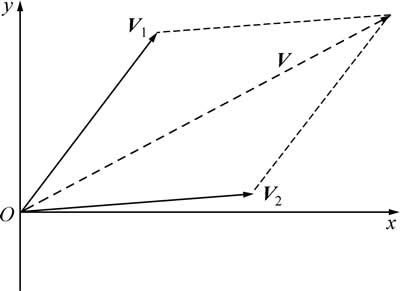
图4 目标偏航轨迹合成示意图
Fig. 4 Vectors synthesis for target trajectory with specific angle yaw
将方向矢量的横坐标归一化,得:V1=(1,K1),V2=(1,K2),V=(1,K)。根据矢量合成的平行四边形法则,结合式(13),有
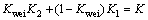 (14)
(14)
目标角度系数由下式计算:
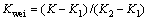 (15)
(15)
其中,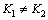 ,符合实际情况。当目标轨迹向左偏转时,K取正值;当目标轨迹向右偏转时,K取负值。Kwei由式(15)决定。
,符合实际情况。当目标轨迹向左偏转时,K取正值;当目标轨迹向右偏转时,K取负值。Kwei由式(15)决定。
2.3 回放-纠正确定目标角度系数准确值
利用矢量合成法确定目标角度系数时,假设质心轨迹为1条方向不变的直线,但实际上往往不是1条直线。当周期T为3 s,步长Fs为290 mm 时,离线和在线生成的质心轨迹如图5所示,其中,Kwei=0和Kwei=1.00分别代表离线、预观控制生成的质心轨迹。
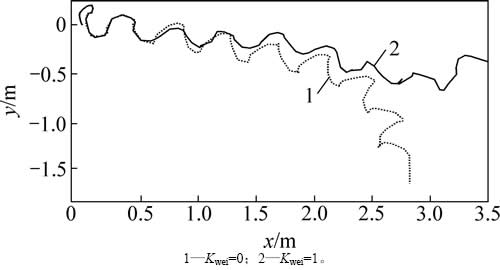
图5 T=3 s,Fs=290 mm时的质心轨迹
Fig. 5 Lateral trajectories of center of mass when T=3 s and Fs=290 mm
如图5所示,离线生成的质心轨迹一直向右偏转,前进2.0 m后偏航明显加剧。预观控制生成的轨迹略微向右偏转,最后向左反向偏转,这给V1和V2的确定带来了误差,因此,矢量合成法计算的角度系数往往与目标要求有偏差,需要进一步修正。
回放-纠正法作为一种学习方法,操作简单灵活,能够快速找到目标解,在机器人导航、示教等领域应用广泛。本文使用该方法的简化形式来确定目标角度系数,流程如下:
1) 离线生成步态,记录质心轨迹;
2) 在线生成步态,记录质心轨迹;
3) 矢量合成,确定满足目标偏航角度的角度系数模糊值;
4) 使用模糊角度系数,生成实际质心轨迹,比较该轨迹方向和目标轨迹方向的偏差,重新修正角度系数;
5) 不断重复第4)步,直到获得目标偏航角度的质心轨迹为止。
3 结果与分析
为了验证算法的有效性, 采用MATLAB 和 Adams 组成的联合仿真平台。在每组仿真工况下,分别记录离线算法、预观控制算法、本文算法生成的质心轨迹。
10自由度样机模型见图6,相应的物理参数和仿真参数见表1。表1中,躯干高度、大腿长度、小腿长度、总体质量、躯干质量、腿部质量、髋关节宽度、髋关节宽度和足部长、宽均为实际样机的物理参数;

图6 机器人模型
Fig. 6 Robot models
表1 模型参数与仿真参数
Table 1 Model parameters and simulation parameters
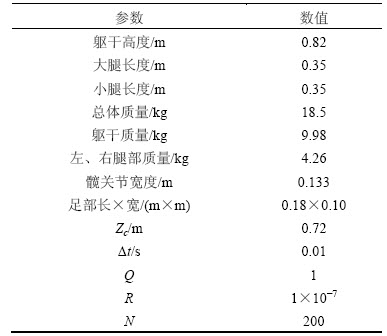
Zc为规划的机器人稳定行走时的质心高度。
3.1 质心侧向轨迹跟踪误差分析
为了验证该算法降低质心侧向轨迹跟踪误差(Ey)的作用,采用杆式模型在MATLAB中进行数值仿真。
步行周期T=4 s,步长Fs=300 mm,角度系数Kwei=0.5。将这3种方法的质心侧向轨迹与规划的参考质心侧向轨迹求差,得到相应的跟踪误差,见图7。这3种方法产生的跟踪误差差别不大,但椭圆区域内峰值相差很大。
与离线生成模式相比,使用角度系数的方法使质心侧向轨迹的跟踪误差降低至少44.9%(由12.16 mm降到 6.69 mm,区域Ⅷ)。与预观控制器相比,本文提出的方法在大部分区域都能有效降低误差绝对极大值(从133.91 mm降到-53.38 mm区域Ⅴ)。
3.2 无偏航直线行走
针对多组步态参数,规划相应的直线行走参考ZMP轨迹,并利用本文提出的方法减少偏航。在不同的步态模式中,给出机器人实际质心在地面的投影轨迹(y-x)来判断是否达到目标。为了便于分析,对实际轨迹进行最小二乘拟合。
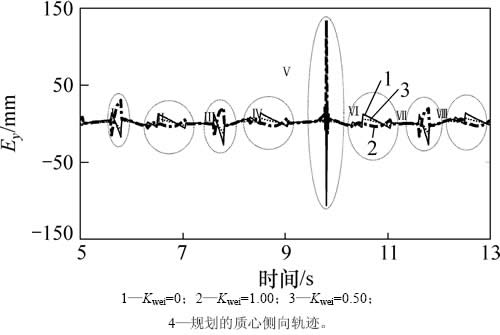
图7 质心轨迹和误差
Fig. 7 COM trajectory and tracking error
由表1可知:髋关节的宽度为133 mm,当机器人质心侧向位移在连续3个周期内的绝对最大值不超过150 mm时,则认为机器人无偏航。由于在本算法中,起步阶段只采用离线生成的角度,故轨迹曲线的方向矢量要从起步阶段完成之后才开始计算。
T=2 s,Fs=260 mm的步态模式对应的质心轨迹见图8。其中,图8(a)中Kwei为0,1.00和0.74时对应曲线分别代表离线、预观控制、角度系数为0.74时生成的质心轨迹曲线,图8(b)所示为其相应的最小二乘拟合轨迹曲线。
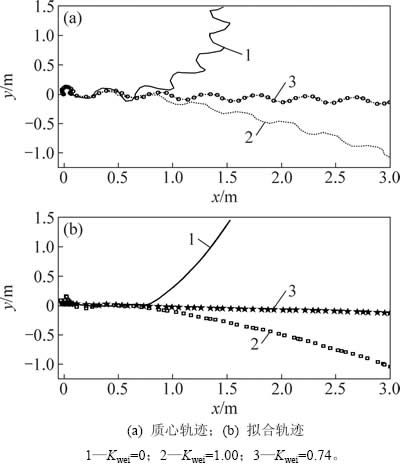
图8 T=2 s,Fs=260 mm时的质心轨迹
Fig. 8 COM trajectory when T=2 s and Fs=260 mm
图8中,离线生成的质心位移矢量不是直线,取方向矢量中的纵坐标K1=1.00;预观控制生成的轨迹曲线可取方向矢量纵坐标K2=-0.25,由式(15)计算0°偏航轨迹直线对应的模糊角度系数Kwei= 0.80。
通过回放-纠正,确定最终的系数为0.74,见图8中Kwei=0.74对应的轨迹曲线:前3.00 m中最大侧向偏移为-0.130 m,基本实现了无偏航行走。
图9所示为步行周期3 s、步长变化时3种方法生成的质心轨迹,最大偏航位移见表2。
图9表明:在不同步态参数下,离线算法和预观控制算法生成的轨迹往往有较大偏转,而提出的矢量合成法有效抑制了偏航。表2表明:与离线步态相比,本方法生成的轨迹偏航数值最小减少65%(从0.334 m下降到0.115 m),最大降幅达到85.4%(从-1.298 m降到-0.190 m),基本实现无偏航行走。
3.3 目标角度偏航行走
针对不同的步态参数,验证算法对机器人左、右各15°和30°偏航的控制效果,轨迹分别如图10和图11所示。在图10(a)中,以向左偏航15°为例,机器人
以T=2 s,Fs=260 mm行走(见图10 (a)中曲线4),在前0.26 m处于起步和偏航过渡阶段;在0.26~4.00 m阶段,轨迹过点(0.26,0.02)和(3.50,1.00),斜率K=0.302,对应角度为16.8°,与15°时的偏差为12%,基本满足目标轨迹要求。按此计算方法,统计不同步态参数下实际偏航角度,结果见表3。
表2 T=3 s时轨迹偏转极大值
Table 2 Maximal yaw values when T=3s mm
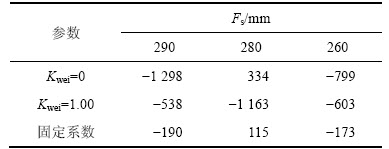
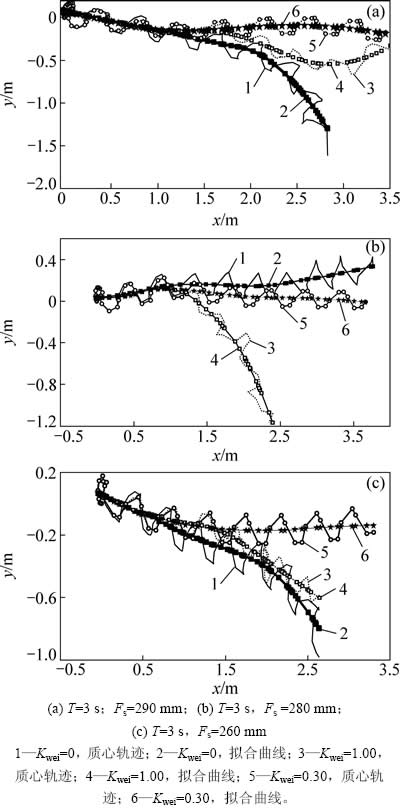
图9 不同步态参数下无偏航行走轨迹
Fig. 9 Trajectory without yaws under different parameters
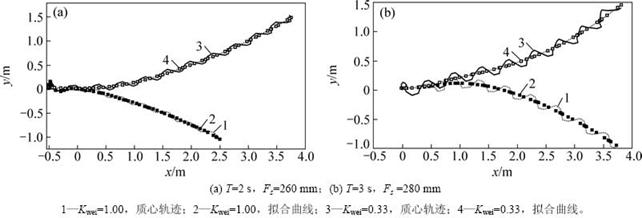
图10 左、右15°偏航轨迹
Fig. 10 Trajectories with right and left 15° yaw
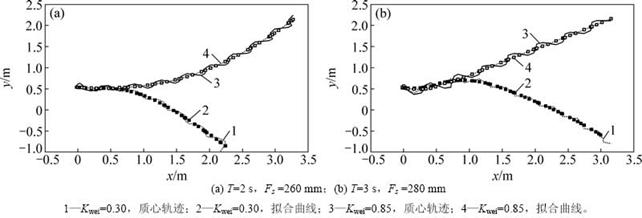
图11 左、右30°偏航轨迹
Fig. 11 Trajectories with right and left 30° yaw
表3 轨迹偏航角度
Table 3 Trajectories yaw angles

表3表明:对于目标15°偏航轨迹,当T=2 s,Fs=260 mm时,最大角度偏差为34%;当T=3 s,Fs= 280 mm时,最大偏差为14%。对于目标30°偏航轨迹,当T=2 s,Fs=260 mm和T=3 s,Fs=280 mm时最大角度偏差不超过15%。这说明该算法能在机器人实际行走过程中有效地控制机器人偏航角度。
4 结论
1) 建立了基于ZMP稳定判据的离线步态生成器和基于预观控制的在线步态生成器;提出角度系数概念,运用矢量合成法和回放-纠正法获得了满足目标偏航角度的角度系数。所提出的方法可实现不同周期、步长的双足步态模式的在线生成,能有效减少质心侧向轨迹跟踪误差,实现不同周期、步长参数下无偏航步态的在线生成,不需要实时规划参考ZMP轨迹,实现15°和30°偏航。
2) 机器人在起步阶段可能发生的偏转会影响实际轨迹,使之与目标轨迹有一定的偏差。下一步将进一步研究该问题,将本文的算法用于实际样机的行走控制中。
参考文献:
[1] 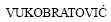 M, STEPANENKO J. On the stability of anthropomorphic systems[J]. Mathematical Biosciences, 1972, 15(1): 1-37.
M, STEPANENKO J. On the stability of anthropomorphic systems[J]. Mathematical Biosciences, 1972, 15(1): 1-37.
[2] 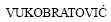 M, BOROVAC B. Zero-moment point-thirty five years of its life[J]. International Journal of Humanoid Robotics, 2004, 1(1): 157-173.
M, BOROVAC B. Zero-moment point-thirty five years of its life[J]. International Journal of Humanoid Robotics, 2004, 1(1): 157-173.
[3] HUANG Q, KAJITA S, KOYACHI N, et al. A high stability, smooth walking pattern for a biped robot[C]//Proceedings of 1999 IEEE International Conference on IEEE. Detroit, USA, 1999: 65-71.
[4] KAGAMI S, KITAGAWA T, NISHIWAKI K, et al. A fast dynamically equilibrated walking trajectory generation method of humanoid robot[J]. Autonomous Robots, 2002, 12(1): 71-82.
[5] MITOBE K, CAPI G, NASU Y. A new control method for walking robots based on angular momentum[J]. Mechatronics, 2004, 14(2): 163-174.
[6] KOMURA T, LEUNG H, KUDOH S, et al. A feedback controller for biped humanoids that can counteract large perturbations during gait[C]//Proceedings of the 2005 IEEE International Conference on Barcelona. Spain: IEEE, 2005: 1989-1995.
[7] KIM J Y, PARK I W, OH J H. Experimental realization of dynamic walking of the biped humanoid robot KHR-2 using zero moment point feedback and inertial measurement[J]. Advanced Robotics, 2006, 20(6): 707-736.
[8] HARADA K, KAJITA S, KANEKO K, et al. An analytical method for real-time gait planning for humanoid robots[J]. International Journal of Humanoid Robotics, 2006, 3(1): 1-19.
[9] KAJITA S, KANEHIRO F, KANEKO K, et al. Biped walking pattern generation by using preview control of zero-moment point[C]//Robotics and Automation, Proceedings, 2003: 1620-1626.
[10] DIEDAM H, DIMITROV D, WIEBER P B, et al. Online walking gait generation with adaptive foot positioning through linear model predictive control[C]//Intelligent Robots and Systems. IEEE/RSJ International Conference on IEEE, 2008: 1121-1126.
[11] CZARNETZKI S, KERNER S, URBANN O. Observer-based dynamic walking control for biped robots[J]. Robotics and Autonomous Systems, 2009, 57(8): 839-845.
[12] SHIMMYO S, SATO T, OHNISHI K. Biped walking pattern generation by using preview control based on three-mass model[J]. IEEE Transactions on Industrial Electronics, 2013, 60(11): 5137-5147.
[13] HIRABAYASHI T, UGURLU B, KAWAMURA A, et al. Yaw moment compensation of biped fast walking using 3D inverted pendulum[C]//2008 10th IEEE International Workshop on Advanced Motion Control. Trento, Italy; IEEE, 2008: 296-300.
[14] CISNEROS R, YOKOI K, YOSHIDA E. Yaw moment compensation by using full body motion[C]//2014 IEEE International Conference on Mechatronics and Automation (ICMA). Tianjin, China: IEEE, 2014: 119-125.
[15] STROM J, SLAVOV G, CHOWN E. Omnidirectional walking using zmp and preview control for the nao humanoid robot[M]//RoboCup 2009: robot soccer world cup XIII. Heidelberg: Springer, 2010: 378-389.
[16] YEON J S, PARK J H. A Fast Turning Method for Biped Robots With Foot Slip During Single-Support Phase[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(6): 1847-1858.
[17] TZUU-HSENG S L, YU-TE S, SHAO-WEI L, et al. Walking motion generation, synthesis, and control for biped robot by using PGRL, LPI, and fuzzy logic[J]. Transactions of Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 41(3): 736-748.
[18] KAGAMI Y, EMURA T, HIYAMA M. Vision-based playback method of wheeled mobile robots[J]. Robotica, 2000, 18(3): 281-286.
[19] 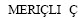 , VELOSO M. Biped Walk Learning Through Playback and Corrective Demonstration[C]//AAAI 2010: Twenty-fourth Conference on Artificial Intelligence. Atlanta, GA, United States: AAAI, 2010: 1594-1599.
, VELOSO M. Biped Walk Learning Through Playback and Corrective Demonstration[C]//AAAI 2010: Twenty-fourth Conference on Artificial Intelligence. Atlanta, GA, United States: AAAI, 2010: 1594-1599.
[20] KATAYAMA T, OHKI T, INOUE T, et al. Design of an optimal controller for a discrete time system subject to previewable demand[J]. Int J Control, 1985, 41(3): 677-699.
(编辑 陈灿华)
收稿日期:2015-07-17;修回日期:2015-09-30
基金项目(Foundation item):国家自然科学基金资助项目(51175383)(Project (51175383) supported by the National Natural Science Foundation of China)
通信作者:肖晓晖,博士,教授,从事特种机器人技术与机器人动力学研究;E-mail:xhxiao@whu.edu.cn