
DOI: 10.11817/j.issn.1672-7207.2021.02.032
风沙铁路道床多尺度模型建立及力学特性分析
张智海1, 2,肖宏1, 2,崔旭浩1, 2,闫东伟1, 2
(1. 北京交通大学 土木建筑工程学院,北京 100044;
2. 北京交通大学 轨道工程北京市重点实验室,北京 100044)
摘要:为了研究沙粒侵入对有砟道床宏细观力学特性的影响,采用离散单元法构建风沙铁路钢轨-轨枕-道床一体化分析模型,提出利用“块体叠加拼装法”快速建立多元混合颗粒体系的建模方法,运用玫瑰图分析道床中道砟颗粒体系接触方向各向异性变化规律,开展风沙铁路道床支承刚度试验,验证离散元模型的正确性。在此基础上,对2种道床的宏细观力学特性进行分析。研究结果表明:道床沙化改变了原有道床的受力体系,使道床受力更加均匀;风沙道床支承刚度增大约48.95%,道砟平均接触力减小约6.38%;沙粒的侵入使道床内部道砟接触方向呈现各向异性,且随着轨枕位移的增大,道砟接触方向各向异性受沙粒的影响越显著;沙粒作用使道床顶部应力减小4.2%,底部应力增大26.78%,可能导致基础顶面应力变大;在循环荷载作用下,沙粒的侵入使道砟颗粒之间的咬合作用减弱,道床累积沉降量明显增大,循环软化行为更强。
关键词:风沙铁路;有砟道床;离散单元法;接触力;累积变形
中图分类号:U213.7 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2021)02-0635-13
Multi-scale model establishment and mechanical analysis of railway ballast bed in sandstorm area
ZHANG Zhihai1, 2, XIAO Hong 1, 2, CUI Huhao 1, 2, YAN Dongwei1, 2
(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. Beijing Key Lab of Track Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: To study the effect of sand intrusion on the macroscopical and micromechanical properties of ballast bed, a sandy ballast bed model was established based on the discrete element method, including rail-sleeper-ballast integrated analysis model. Multifold particles system of sandy ballast bed padded by using "block stacking assembly method" was proposed. The contact direction's anisotropy law of ballast particle system was tested by drawing a rose diagram. The stiffness test of wind sandy railway ballast bed was conducted to verify the correctness of a discrete element model. On this basis, the macroscopic and microscopic mechanical properties of the two kinds of bed were analyzed systematically. The results show that ballast bed desertification changes the automated system of the original ballast bed, and the stress of the bed is more uniform. Support stiffness of sandy ballast is about 48.95% higher than that of ballast bed without sand, and the average ballast contact force decreases by about 6.38%. The invasion of sand makes the contact direction of ballast show anisotropy. With the increase of sleeper displacement, the anisotropy of ballast contact direction is more obvious. The stress at the top of the bed reduces by 4.2% and at the bottom increases by 26.78%, resulting in the stress at the top of the foundation. Under the action of cyclic load, the interlock between ballast particles is reduced by the intrusion of sand particles, the cumulative settlement of ballast bed is obviously increased, and the cyclic softening behavior is stronger.
Key words: sandy railway; ballast bed; discrete element method; contact force; cumulative deformation
有砟轨道是铁路最基本的轨道结构形式之一,道床是轨道结构的主要组成部分,具有保持轨道的稳定性、减缓和吸收轮轨的冲击和振动、良好的排水性能等作用[1]。我国是世界上沙漠化最严重的国家之一,尤其是西北地区地势地形条件复杂,气候条件恶劣,荒漠化严重,道床沙化成为这些地区铁路道床的主要病害。沙粒的贯入沉积填充了道砟颗粒间的空隙,改变了道床的粒径级配和弹性,引起了一系列工务病害,如:造成道床板结失去弹性,轨道结构刚度增大,轮轨接触区动力响应变大,钢轨波磨和车轮磨耗加剧,道床排水能力下降,道床养护维修困难等[2-3];而且沙粒中含有大量盐分,在雨水作用下还会引起钢轨和扣件锈蚀[4-6],这些都会导致轨道结构使用性能下降,线路服役状态变差,严重影响列车运行的效率和安全性[7]。因此,对风沙地区铁路系统进行深入研究具有重要的意义。
风沙道床是指由不同粒径的碎石道砟和沙粒组成的一种非连续、非均匀、多尺度效应显著的复杂混合多相介质,内部受力和变形机理复杂。目前,已有诸多学者开展了相关研究。在试验研究方面,FACCOLI等[8]针对轮轨接触面有沙和无沙2种试验条件,利用双盘试验台进行了车轮滚动和滑动试验,结果表明,沙粒的存在显著增加了车轮的磨损率。CARRASCAL等[9]对风沙地区高速铁路扣件进行了室内模拟试验,结果表明,沙粒的存在会影响整个扣件系统的使用性能,而对单个扣件影响不大。TOLOU等[10-11]对风沙区铁路开展了现场试验,结果表明,沙粒侵入提高了道床的刚度,改变了轨枕的受力方式,且随着道床沙粒含量的增加,混凝土轨枕下的压力分布逐渐趋于均匀。ESMAEILI等[12]针对风沙道床,开展了不同含沙量道砟箱循环载荷试验,结果表明,随着含沙量的增加,试样累积沉降不断增大,提出利用轮胎衍生骨料(tire derivative aggregate)来改善含沙道床的受力性能。在数值模拟方面,严颖等[13]针对风沙区有砟道床的结构特性,采用离散单元法建立了桶状试样对道砟和细沙颗粒进行了数值模拟,并从沙石混合体的力链强度、空间分布及配位数等细观角度对不同含沙率下的有效变形模量进行了分析,结果表明低含沙率对沙石混合体变形模量影响不大。综上所述,已有研究主要针对风沙区铁路道床变形及稳定性方面,而对风沙作用下道床动态性能演变规律及细观分析的研究较少。
基于此,本文作者采用“块体叠加拼装法”,建立钢轨-轨枕-道床离散元分析模型,解决在多尺度效应影响下风沙道床全尺寸模型难以建立的问题,从宏细观角度分析道砟与沙粒相互作用下道床的力学特性演变规律,揭示风沙道床受力与变形工作机制,为我国西北地区大范围风沙铁路道床设计和沙害防治提供理论依据。
1 计算模型的建立
风沙铁路道床含沙量大,沙粒粒径小,道砟粒径大,多尺度效应显著,利用PFC3D建立风沙道床全尺度模型,会存在颗粒数较多、模型平衡困难、计算效率低下等问题。因此,本文利用PFC2D离散元分析软件进行模拟。
“块体叠加拼装法”是建立多元混合铁路道床离散元模型的一种有效的建模方法,主要是由块体叠加法与块体拼装法2部分构成。该法建模效率高、平衡时间短、建模灵活,可以将复杂结构拆分成多个简单的块体,其突出优势是解决了多元混合颗粒体系及复杂模型生成困难的问题。“块体叠加拼装法”建模流程见图1。

图1 块体叠加拼装法建模步骤
Fig. 1 Modeling steps of block stacking assembly method
1.1 不规则道砟颗粒生成
铁路道砟形态各异,棱角分明,极不规则。为建立比较精细的道砟颗粒模型,考虑到道砟的边-角、角-角等的接触方式不同以及道砟颗粒之间的互锁现象,在铁路线路风沙作用段,随机挑选椭圆形、棱形、细长形道砟各3枚作为样本,利用MATLAB图像处理技术提取道砟廓形,采用fish语言构建了道砟样本库模板,从而生成不规则的道砟颗粒,见图2。根据行业标准TB/T 2140—2008“铁路碎石道砟”,考虑到风沙段铁路现场的实际道砟级配分布,按照既有线一级碎石道砟粒径级配曲线中的红色曲线(见图3)生成道砟模型。

图2 部分不规则道砟颗粒建模过程
Fig. 2 Part of modeling process of irregular ballast particles

图3 一级碎石道砟粒径级配
Fig. 3 Gradation of grain size of first-grade gravel ballast
1.2 块体叠加法生成沙石混合块体模型
块体叠加法是指将大小相同、颗粒类型均一的块体合并为一个块体模型。叠加块体建模过程为:
1) 采用圆盘颗粒(ball)模拟沙粒,考虑到细沙和中沙的颗粒粒径与道砟颗粒粒径相差悬殊,为提高模型计算效率,在计算结果可接受的范围内,将沙粒粒径放大10倍[13],生成长×宽为300 mm×100 mm密实的子块体,再拼装成长×宽为600 mm×300 mm的纯沙块体模型(见图4(a))。
2) 采用簇颗粒(clump)模拟道砟,按照级配生成长×宽为600 mm×300 mm的道砟块体模型,如图4(b)所示。
3) 将相同尺寸的纯沙块体与道砟块体进行叠加,生成的混合块体模型(图4(c))。
4) 考虑到填充效果,分别按照图4(f)和4(g)进行沙粒粒径缩放,采用自编fish语言将图4(d)中道砟廓形范围内的沙粒删除。
5) 将沙粒粒径恢复初始状态,重新平衡,实现道砟空隙的近似完全填充,生成了道砟-沙粒的混合块体模型,如图4(e)所示。

图4 道砟-沙子混合块体离散元模型建立过程
Fig. 4 Processes of establishing discrete element model of ballast-sand mixed block
1.3 块体拼装法生成道床模型
块体拼装法是将多个块体进行装配,形成一个系统的数值仿真计算模型。结合现场试验段的实际情况,根据我国“铁路轨道设计规范”,取道床断面顶面宽度为3.5 m,厚度为0.35 m,边坡坡度为1.00:1.75,轨枕采用新Ⅱ型混凝土枕。拼装过程为:
1) 将道砟-沙粒混合块体模型复制20次,拼接形成初始的风沙段道床,再重新平衡,消除块体之间的接缝,如图5(a)所示。

图5 模型局部放大图
Fig. 5 Model details
2) 将轨枕CAD图形交换文件导入PFC2D中,设置周期性边界条件,进行颗粒填充生成轨枕离散元块体模型。
3) 采用60 kg/m钢轨,模型生成方法与轨枕生成方法类似。
4) 将道床、轨枕、钢轨块体进行组装,最终生成风沙段钢轨-轨枕-道床一体化模型(图6(a))。
为更好地揭示风沙道床的力学特性,利用“块体叠加拼装法”建立了没有沙粒贯入的普通有砟道床模型进行对比分析,如图6(b)所示。离散元模型中钢轨密度和轨枕密度分别为7 850 kg/m3和2 500 kg/m3;道砟颗粒密度和砂粒密度分别为2 600 kg/m3和2 650 kg/m3。

图6 钢轨-轨枕-道床一体化模型
Fig. 6 Rail-sleeper-ballast integration models
参照已有研究[14-17],离散元模型计算参数如表1所示。基于Mohr-Coulomb准则的滑动摩擦和Mindlin理论[13],考虑沙粒-道砟之间无黏聚力,采用线性接触模型计算颗粒之间的接触力,计算公式如下:
 (1)
(1)
 (2)
(2)
式中,Fn为法向接触力;Kn为法向接触刚度;Un为颗粒之间法向相对位移;Fs为切向接触力;Ks为切向接触刚度;Us为颗粒之间切向相对位移。
表1 模型计算参数
Table 1 Model calculation parameters

2 模型验证及荷载施加
2.1 模型的可靠性验证
为验证风沙段与普通无沙段钢轨-轨枕-道床一体化离散元模型微观参数的正确性,分别选取普通无沙段与风沙段开展了现场道床支承刚度试验,如图7所示。数值仿真与现场试验结果,如图8所示。

图7 现场道床支承刚度试验
Fig. 7 Test for stiffness of ballast support

图8 轨枕力与位移的关系
Fig. 8 Relationship between sleeper force and displacement
由图8可知,风沙段轨枕力与位移曲线比普通无沙段的陡,且变化速度较快,说明风沙道床支承刚度较大。此外,数值模拟轨枕力与位移关系曲线与现场试验结果较为相似,数据吻合度较高。第i组试验的道床支承刚度Fi为
 (3)
(3)
式中,D35为35 kN处的位移;D7.5为7.5 kN处的位移。
由计算结果可知,风沙段支承刚度平均值比普通无沙段刚度平均值大61 kN/mm,道床支承刚度提高了约48.95%。这主要是由于道砟孔隙被沙粒填充,道床失去弹性,使道床支承刚度增大。这与文献[10-11]的研究结果一致。此外,普通无沙道床支承刚度试验平均值与数值模拟仿真值相对误差仅为0.49%;风沙道床支承刚度试验平均值与数值模拟仿真值相对误差为2.90%,相对误差均较小,说明了离散元模型可靠度高,可用于道床力学特性研究。
2.2 列车荷载施加
在散体道床室内试验和数值模拟研究中,许多学者采用正(余)弦荷载来模拟列车荷载,进行道砟箱循环荷载试验[16-17]、高速铁路道砟累积变形试验[18]、RTF(railway test facility)列车荷载模拟试验[19]等。基于此,本文考虑轨枕荷载分担系数,取中间轨枕分担系数为0.5,以铁路线路运营的C64K货车实际轴重为依据,荷载半峰值F取63 kN,将余弦荷载直接施加在钢轨上,具体荷载公式如下:
 (4)
(4)
式中:F为施加在钢轨上的荷载半峰值;t为加载时间;f为加载频率,考虑到列车运行速度一般为30~50 km/h,运行时速较低,荷载频率取5 Hz。在加载过程中,严格保证左右钢轨同时施加余弦荷载。
3 计算结果分析
3.1 道床内部微观接触力分析
散体道床的道砟接触力直接影响道砟的劣化速度和使用寿命。已有研究表明,当道砟接触力不超过10 kN时,道砟的破碎概率很小[20]。图9所示为风沙段与普通无沙段道床在20次循环荷载作用下的道砟平均接触力变化曲线。
由图9可知,风沙段道砟平均接触力为44 N,普通无沙段道砟平均接触力为47 N,风沙段道砟平均接触力比普通无沙段平均接触力小6.38%左右。这是由于风沙段道床含有大量细沙,改变了道砟颗粒之间原有的受力关系,沙粒和道砟共同承担上部列车荷载,使单个道砟的平均接触力减少,力的传递和分配速度变慢。

图9 道砟平均接触力
Fig. 9 Ballast average contact force
在道床平均接触力稳定阶段,利用fish语言提取道砟颗粒接触力,绘制峰值荷载作用下风沙段和普通无沙段道床内部接触力分布云图,如图10所示。从图10可见:轨枕下方绿色区域(受力较小区域)面积少,而砟肩下全为绿色区域,说明道床受力主要集中在轨枕下方区域,与砟肩以下范围关系不大;此外,风沙段红色区域面积(受力较大区域)明显减少,绿色区域明显增大,说明沙粒的侵入会减小道砟颗粒之间的接触力,使道床内部受力更加均匀。因此,单从接触力来看,风沙道床有利于延缓道砟破碎。

图10 峰值荷载作用下道床内部接触力分布
Fig. 10 Distribution of internal contact force under peak load
3.2 颗粒细观力链演化规律分析
3.2.1 道砟接触力
为准确表征荷载作用下沙粒侵入对道砟颗粒法向接触力与切向接触力方向的各向异性的影响,参考张强等[21-22]提出的颗粒间接触力分布描述方法,对不同轨枕位移下的道砟法向接触力进行统计,并按接触角度进行分组,通过自编fish语言进行颗粒接触信息处理,利用自编小程序绘制了法向接触力分布玫瑰图,如图11所示。图11中,同心圆表示各组法向接触力合力等级,绘图基准力为4 kN;0°~360°为法向合力方向。切向接触力统计方法与法向接触力统计方法类似,绘图基准力为2 kN,如图12所示。

图11 道砟颗粒间法向接触力的统计分布
Fig. 11 Statistical distribution of normal contact force between ballast particles

图12 道砟颗粒间切向接触力的统计分布
Fig. 12 Statistical distribution of tangential contact forces between ballast particles
由图11可知,风沙段各组接触法向合力明显比普通无沙段的小,接触法向合力平均值为普通无沙段的1/3~1/4;普通无沙段道砟接触法向合力呈“8”字形分布,风沙段道砟接触法向合力呈“K”字形分布。普通无沙道床受重力作用,初始阶段法向接触力很小,集中在1个小圆点内,但由于道床本身是各向异性的散体颗粒材料,小圆点也呈不规则形状。将最大接触合力分组的方向记为主分布方向,可以发现,随着道床位移增大,主分布方向的法向接触力逐渐增大,最大接触法向合力集中在90°附近,而在0°方向上,接触法向合力无明显变化。这与道床垂向受力有关,也说明随着道床位移的增大,普通无沙段道床接触法向方向各向异性增强。风沙段道床在未加载时,法向接触力分布廓形与普通无沙段的相似,随着道床位移的增大,在0°和90°左侧方向上,接触法向合力无明显变化;在90°右侧,接触法向合力逐渐增大,出现明显接触方向偏向性。沙粒的侵入使道床受力体系发生明显变化,风沙道床道砟接触方向各向异性更显著,这与接触方向分布偏向性密切相关。
由图12可知:风沙段各组切向接触合力比普通无沙段的小,平均切向接触合力为普通无沙段的1/3~1/4;普通无沙段道床颗粒间切向接触合力呈“蝴蝶状”分布;风沙道床颗粒间切向接触合力呈“花瓣状”分布。在初始阶段,道床内部几乎不受剪,颗粒切向接触合力几乎为0,表现出切向接触方向的各向同性;此后,随着道床位移增大,切向接触合力逐渐增大,但普通无沙道床颗粒之间的切向接触合力增大幅度明显比风沙道床的大。这是由于风沙道床含沙量大,沙粒承受了部分压力,随着沙粒逐渐密实,道砟颗粒原有的接触被沙粒挤开,接触数量减少,道砟承担的压力也变小。此外,风沙道床颗粒切向接触合力方向出现明显的偏向性,具体表现为0°~180°范围内的颗粒接触密度和切向接触合力比180°~360°范围内的小,即在沙粒的影响下,道砟颗粒重新排列,颗粒之间的切向接触力重新分配,导致风沙道床切向力方向各向异性更为显著,也验证了道床是由各向异性极强的散粒体组成。
3.2.2 沙粒接触力
图13所示为沙粒接触力统计分布,其中,红色线代表风沙段接触力的模拟结果,绿色线代表风沙段平均接触力合力。为更清晰地统计沙粒的接触力,将绘图基准力设为道砟颗粒接触力的2倍。由图13可知:随着道床位移的增加,沙粒接触合力越来越大,为道砟接触合力的3.0~3.5倍。由图13(a)~(c)可知:初始阶段沙粒之间的法向接触力很小几乎为0,随着道床位移的增大,法向接触力大致呈“花生状”分布,最大接触力与最小接触力之比较小,分布主方向不是很明显,内部受力较为均匀。由图13(d)~(f)可知:初始阶段沙粒的切向接触力合力趋向于0,表现出各向同性,但随着道床位移的增大,切向接触力大致呈比较对称的“花瓣状”分布,没有出现接触方向偏向性。这是由于道床中沙粒的数量远远大于道砟颗粒数量,道床内颗粒之间力的传递发生了很大变化,出现了接触力的分散迁移现象,沙粒逐渐成为受力主体。

图13 沙粒接触力统计分布
Fig. 13 Statistical distribution of sand contact force
3.3 道床应力分析
荷载稳定阶段道床不同深度的应力如表2所示。由表2可知:在峰值荷载作用下,道床内部应力沿深度呈衰减趋势,普通无沙段道床应力衰减幅度更明显;在深度0.05 m处,风沙道床应力减小4.2%,在深度0.3 m处,风沙道床应力增加26.78%。这主要是由于风沙段沙粒的数量远远大于道砟颗粒的数量,道床容重显著增大,导致自重应力成为影响道床下部应力差异的关键因素。随着深度增加,自重应力呈线性增大,在列车荷载作用下,道床应力呈下降趋势,自重应力对道床上部影响很小,而对于道床下部应力影响显著。
表2 道床不同深度应力峰值
Table 2 Stress peaks at different depths of bed MPa
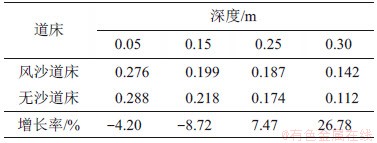
此外,风沙道床上部应力比普通无沙道床的小,下部应力比普通无沙道床的大。这是因为上部含沙量大,承受荷载的沙粒比较多,力的传播途径多,单位区域内应力减小。虽然沙粒的侵入使道床内部接触面积增大,应力传播方向增多,平均每个颗粒接触力减小,但力的传递需要一定时间,在有限的时间内不能均匀传递,造成下部道床应力衰减速率较慢,而且空隙率越低,能量耗散越慢,风沙道床空隙率较低,单位时间耗散能比普通无沙段的小,作用在系统的能量比较大,导致单位区域受力比较大,荷载应力衰减速度变慢,加之自重应力增大,从而出现道床下部应力增大现象。
3.4 道床累积沉降分析
道床累积沉降是列车荷载和外界自然环境长期作用的结果,且随着变形的累积,轨道不均匀下沉,轨道结构稳定性降低,影响行车安全。图14所示为循环荷载作用下风沙段道床和普通无沙段道床沉降变形曲线。

图14 道床累积沉降曲线
Fig. 14 Cumulative settlement curves of bed
由图14可知:初始加载阶段,风沙道床累积沉降与普通无沙道床的相差不大,但随着荷载作用次数的增加,风沙道床累积沉降变化幅度明显比普通无沙道床的大;普通无沙道床的沉降约在荷载作用10次后基本趋于稳定,而风沙道床的沉降直到荷载作用60次后才基本稳定。这主要是由于道床在循环荷载作用下,沙粒逐渐成为受力主体,颗粒之间以单点接触为主,道砟与道砟之间的接触减少,道砟之间的咬合作用及互锁效应减弱,使颗粒之间的滑移增大,从而使沉降收敛速率变慢,累积沉降增大。这与文献[12]中的规律一致。
风沙道床与普通无沙道床都是散粒体结构,其内部存在一定的空隙,颗粒之间的接触、摩擦、滑移等微观特征,使宏观道床成为非理想性的弹性体,动荷载与相应的动位移在1个循环内形成了滞回圈[23]。滞回环与荷载作用次数的关系如图15所示。图中,f1为初始荷载;f2为荷载峰值;x1和x2为对应荷载的位移。由图15可知:经历1个完整的荷载作用周期后,终点位置(C点)与道床的荷载作用前的起始位置(A点)并未完全重合,A点与C点之间的横坐标差值表现为道床在经历该荷载周期后的沉降累积。随着荷载作用次数的增加,A点与C点间的横坐标差值越来越小,并逐渐趋向于0,这反映了道床沉降逐渐趋于稳定。但风沙道床相邻滞回环的横坐标差值df比普通无沙段的大,说明风沙道床塑性变形较大。这与道床中颗粒数量及颗粒之间的相对滑移密切相关。

图15 滞回环与荷载作用次数的关系
Fig. 15 Relationship between hysteresis ring and load times
根据荷载作用下轨枕压力-位移曲线,以非线性骨架曲线及Masing原理为基础[23-25],参考Hardin-Drnevich模型的分析过程,绘制滞回能与荷载作用次数的关系曲线,如图15(c)所示。循环加载过程中滞回能滞回环面积△Wp表示,体现了系统能量耗散的能力。滞回环的面积计算公式为:
 (5)
(5)
式中:FBC为卸载力;FBA为加载力。
由图15(c)可知:随着荷载作用次数增加,道床的滞回能呈减小趋势,在前10次荷载作用下,滞回能变化减少幅度较大,之后逐渐趋于稳定,说明道床处于稳定耗能状态。风沙道床耗能能力比普通无沙道床的大,这主要是由于风沙道床含有大量沙粒,沙粒滑移过程中,摩擦作用消耗了大量能量,导致道床能量耗散较多,而且散体道床本身具有塑性流动性,在循环荷载作用下极易出现循环软化,从而使滞回能减小。
4 结论
1) 在动荷载作用下,风沙道床内部颗粒之间接触力明显减小,相比于普通无沙道床,道砟颗粒平均接触力约减少了6.38%,说明风沙道床受力比较均匀,可以减少道砟之间的接触力,减少道砟破碎量。
2) 随着道床位移的增大,风沙道床道砟法向接触力呈“K”字形分布,切向接触力呈“蝴蝶状”分布;而普通无沙道床道砟法向接触力呈“8”字形分布,切向接触力呈“花瓣状”分布,说明风沙道床道砟接触方向的各向异性比普通无沙道床的各向异性更显著,也验证了道床是由各向异性极强散粒体组成。
3) 随着道床深度增加,道床内部应力逐渐衰减,普通无沙道床衰减速度更快,风沙道床上部应力比普通无沙道床的应力小,下部应力比普通无沙道床的应力大,表明沙粒可以减少道床顶部应力,但又增大了道床底部应力,导致下部基础顶面应力增大,可能会使基础沉降增大,影响线路平顺性。
4) 在循环荷载作用下,道床的滞回能都逐渐减少,向稳定的方向发展,但风沙道床累积沉降量比普通无沙道床的大,循环软化行为更强,这与沙粒的侵入改变了道床内部接触关系、颗粒之间的自锁力减弱、颗粒之间滑移量变大等密切相关。
参考文献:
[1] 张徐, 赵春发, 翟婉明, 等. 铁路有砟道床振动和变形的离散元模拟与试验验证[J]. 岩土力学, 2017, 38(5): 1481-1488.
ZHANG Xu, ZHAO Chunfa, ZHAI Wanming, et al. Discrete element simulation and its validation on vibration and deformation of railway ballast[J]. Rock and Soil Mechanics, 2017, 38(5): 1481-1488.
[2] KIAN A R T, ZAKERI J A, SADEGHI J. Experimental investigation of effects of sand contamination on strain modulus of railway ballast[J]. Geomechanics and Engineering, 2018, 14(6): 563-570.
[3] SADEGHI J, KIAN A R T, GHIASINEJAD H, et al. Effectiveness of geogrid reinforcement in improvement of mechanical behavior of sand-contaminated ballast[J]. Geotextiles and Geomembranes, 2020(6): 768-779.
[4] ZAKERI J A. Investigation on railway track maintenance in sandy-dry areas[J]. Structure and Infrastructure Engineering, 2012, 8(2): 135-140.
[5] RAFFAELE L, BRUNO L. Windblown sand action on civil structures: Definition and probabilistic modelling[J]. Engineering Structures, 2019, 178: 88-101.
[6] ZAKERI J A, ESMAEILI M, FATHALI M. Evaluation of humped slab track performance in desert railways[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2011, 225(6): 566-573.
[7] TOLOUKIAN A R, SADEGHI J, ZAKERI J A. Large-scale direct shear tests on sand-contaminated ballast[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2018, 171(5): 451-461.
[8] FACCOLI M, PETROGALLI C, LANCINI M, et al. Effect of desert sand on wear and rolling contact fatigue behaviour of various railway wheel steels[J]. Wear, 2018, 396/397: 146-161
[9] CARRASCAL I A, CASADO J A, DIEGO S, et al. Dynamic behaviour of high-speed rail fastenings in the presence of desert sand[J]. Construction and Building Materials, 2016, 117: 220-228.
[10] TOLOU KIAN A R, SADEGHI J, ZAKERI J A. Influences of railway ballast sand contamination on loading pattern of pre-stressed concrete sleeper[J]. Construction and Building Materials, 2020, 233: 117324.
[11] ZAKERI J A, ABBASI R. Field investigation of variation of loading pattern of concrete sleeper due to ballast sandy contamination in sandy desert areas[J]. Journal of Mechanical Science and Technology, 2012, 26(12): 3885-3892.
[12] ESMAEILI M, AELA P, HOSSEINI A. Experimental assessment of cyclic behavior of sand-fouled ballast mixed with tire derived aggregates[J]. Soil Dynamics and Earthquake Engineering, 2017, 98: 1-11.
[13] 严颖, 狄少丞, 苏勇, 等. 风沙影响下铁路道碴变形模量的离散元数值分析[J]. 计算力学学报, 2012, 29(3): 439-445.
YAN Ying, DI Shaocheng, SU Yong, et al. Discrete element analysis of elastic modulus of railway ballasts in wind with different sand contents[J]. Chinese Journal of Computational Mechanics, 2012, 29(3): 439-445.
[14] 张徐, 赵春发, 翟婉明, 等. 重载铁路有砟道床动态行为的离散元模拟与试验研究[J]. 铁道学报, 2019, 41(4): 169-176.
ZHANG Xu, ZHAO Chunfa, ZHAI Wanming, et al. Discrete element simulation and field test on dynamic behavior of heavy haul railway ballast[J]. Journal of the China Railway Society, 2019, 41(4): 169-176.
[15] TING J M, KHWAJA M, MEACHUM L R, et al. An ellipse-based discrete element model for granular materials[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(9): 603-623.
[16] 亓伟, 刘玉涛, 李成辉. 道砟胶分段固化道床动力性能测试与分析[J]. 中南大学学报(自然科学版), 2018, 49(3): 764-770.
QI Wei, LIU Yutao, LI Chenghui. Dynamic testing and analysis of ballasted track of different stiffness sections using polyurethane ballast reinforcement technique[J]. Journal of Central South University(Science and Technology), 2018, 49(3): 764-770.
[17] 井国庆, 封坤, 高亮, 等. 循环荷载作用下道砟破碎老化的离散元仿真[J]. 西南交通大学学报, 2012, 47(2): 187-191.
JING Guoqing, FENG Kun, GAO Liang, et al. DEM simulation of ballast degradation and breakage under cyclic loading[J]. Journal of Southwest Jiaotong University, 2012, 47(2): 187-191.
[18] 张徐, 赵春发, 翟婉明. 循环荷载频率对高速铁路有砟道床累积变形行为的影响[J]. 中国铁道科学, 2017, 38(1): 1-8.
ZHANG Xu, ZHAO Chunfa, ZHAI Wanming. Influence of cyclic loading frequency on accumulated deformation behavior of high-speed railway ballast bed[J]. China Railway Science, 2017, 38(1): 1-8.
[19] AURSUDKIJ B, MCDOWELL G R, COLLOP A C. Cyclic loading of railway ballast under triaxial conditions and in a railway test facility[J]. Granular Matter, 2009, 11(6): 391-401.
[20] 高亮, 罗奇, 徐旸, 等. 基于离散元法的铁路道床力学特性[J]. 同济大学学报(自然科学版), 2014, 42(7): 1064-1069.
GAO Liang, LUO Qi, XU Yang, et al. Railway ballast bed mechanical property based on discrete element method[J]. Journal of Tongji University(Natural Science), 2014, 42(7): 1064-1069.
[21] 张强, 汪小刚, 赵宇飞, 等. 不同围压加载方式下土石混合体变形破坏机制颗粒流模拟研究[J]. 岩土工程学报, 2018, 40(11): 2051-2060.
ZHANG Qiang, WANG Xiaogang, ZHAO Yufei, et al. Particle flow modelling of deformation and failure mechanism of soil-rock mixture under different loading modes of confining pressure[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2051-2060.
[22] ROTHENBURG L, BATHURST R J. Analytical study of induced anisotropy in idealized granular materials[J]. Géotechnique, 1989, 39(4): 601-614.
[23] 肖杰灵, 刘浩, 刘淦中, 等. 高速铁路有砟道床纵向阻力滞回曲线特征及规律研究[J]. 铁道学报, 2018, 40(2): 91-99.
XIAO Jieling, LIU Hao, LIU Ganzhong, et al. Study on characteristics and law of longitudinal resistance hysteretic curves of ballast bed of high-speed railway[J]. Journal of the China Railway Society, 2018, 40(2): 91-99.
[24] 栾茂田, 林皋. 土料非线性滞回本构模型的半解析半离散构造方法[J]. 大连理工大学学报, 1992, 32(6): 694-701.
LUAN Maotian, LIN Gao. Semi-analytical and semi-discrete procedure for constructing nonlinear hysteretic constitutive model of soils[J]. Journal of Dalian University of Technology, 1992, 32(6): 694-701.
[25] HAYASHIKAWA T, ABDEL RAHEEM S E, HASHIMOTO I. Nonlinear seismic response of soil-foundation-structure interaction model of cable-stayed bridges tower[C]// 13th World Conference on Earthquake Engineering. Vancouver, Canada, 2004: 3045.
(编辑 赵俊)
收稿日期: 2020 -02 -22; 修回日期: 2020 -04 -20
基金项目(Foundation item):国家自然科学基金资助项目(51578055);中央高校基本科研业务费专项资金资助项目(2015JBZ004) (Project(51578055) supported by the National Natural Science Foundation of China; Project(2015JBZ004) supported by the Basic Scientific Research Operating Expenses of Central Universities)
通信作者:肖宏,博士,教授,从事铁道工程研究;E-mail:xiaoh@bjtu.edu.cn
引用格式: 张智海, 肖宏, 崔旭浩, 等. 风沙铁路道床多尺度模型建立及力学特性分析[J]. 中南大学学报(自然科学版), 2021, 52(2): 635-647.
Citation: ZHANG Zhihai, XIAO Hong, CUI Huhao, et al. Multi-scale model establishment and mechanical analysis of railway ballast bed in sandstorm area[J]. Journal of Central South University(Science and Technology), 2021, 52(2): 635-647.