DOI: 10.11817/j.issn.1672-7207.2017.10.010

精密运动平台的五自由度误差同时测量方法

王丽军，郑煜，吕文，李继攀，段吉安

(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)

摘要：提出一种同时测量运动平台五自由度误差的方法。采用准直的激光光束作为基准，仅以角锥棱镜作为误差测量的敏感器件，由1个斜方棱镜和聚焦透镜并辅以光电位移传感器组成测量系统。研究结果表明：直线运动平台2个直线度误差和3个角度误差可同时测量，且测量头无电缆连接；测量直线度误差的分辨率小于0.1 μm，角度误差的分辨率小于1″；直线度和角度测量精度分别达到1 μm和5″。测量系统结构简单，易于安装和调节，适用于运动平台多自由度误差精密测量。

关键词：同时测量；五自由度；运动误差；准直光束；运动平台

中图分类号：TN247             文献标志码：A         文章编号：1672-7207(2017)10-2628-07

Simultaneous measurement of five-degree-of-freedom motion errors of high-precision motion platforms

WANG Lijun, ZHENG Yu, L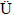 Wen, LI Jipan, DUAN Ji’an

(State Key Laboratory of High Performance Complex Manufacturing,

School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: A quite simple and novel method for simultaneous measurement of five-degree-of-freedom motion errors was proposed. The collimated laser beam was used as the reference line, and only a cube corner prism was adopted in the moving platform as the sensitive element. The optical system was composed of a rhombic prism, a focus lens and three detectors. The results show that the horizontal and vertical straightness errors as well as pitch, yaw and roll angle errors can be measured simultaneously. At the same time, the measuring head is smart and wireless. The resolution of the straightness and angle errors can reach 0.1 μm, 1″, respectively, and the measurement accuracy of straightness errors and angular errors are about 1 μm and 5″within the travel range of a high-precision motion platform. This system is compact and can be easily equipped to any motion platforms to implement the measurement of multi-degree-of-freedom motion errors.

Key words: simultaneous measurement; five-degree-of-freedom; motion errors; collimated beam; high-precision motion platform

精密运动平台是实现微纳级定位和制造的关键技术，在精密机械加工、光电子器件对准耦合、集成电路制造等领域，都需要对目标工件进行多至6个自由度的测量、调整和控制^[1]。以直线运动平台为例，当其沿导轨运动时有6个自由度运动误差，包括定位误差△z、直线度误差△x和△y以及3个角度误差偏摆角△α、俯仰角△β、滚转角△γ。目前，测量这些误差主要还是采用以激光干涉仪为代表的单参数测量方法，每次只能测量1个误差分量，而每个测量过程又需要使用不同类型的测量附件以及重新调整运动平台，测量过程长且结果存在很大的随机性，这显然无法满足运动平台快速测量和调整的要求。因此，研究多自由度误差的精密测量方法与技术对物体位置的精确控制和调整有重要的意义。近年来，基于激光干涉技术^[2-4]、衍射技术^[5-7]、准直技术^[8-9]、视觉测量技术^[10-11]等不同的光学原理，涌现出了多种同时测量运动平台多自由度误差的方法。FAN等^[12-13]提出一种基于四光束基准的六自由度同时测量方法，采用4套多普勒位移测量仪和2个光电探测器，结合L型反射镜和直角棱镜等光学元件，可同时测量直线运动平台的六自由度误差，但结构较复杂且成本较高。LIU等^[14]设计的测量6个自由度的运动误差的系统，由带有特殊光路的微型光纤耦合激光干涉仪和象限探测器集成，在实验条件下，有较高的测量精度，但该系统测量头带有光缆，不适合目标平台快速安装测量。FENG等^[15-16]以准直激光光束为测量基准，利用角锥棱镜、分光片及象限探测器等先后实现了直线导轨四自由度和六自由度同时测量，但测量头整体体积较大，不便于安装在精密短行程运动平台上。本文作者提出一种基于激光准直技术的五自由度误差同时测量方法。测量头采用1个角锥棱镜同时作为直线度和角度的敏感器件，固定部分用1个斜方棱镜和聚焦透镜搭建简易光路，配合高精度的光电位移传感器，实现对精密运动平台的二维直线度及三维转角误差的同时测量。测量系统的光学元件极少且结构简单，测量头为单个镜片，体积较小，无电缆连接，易于安装和调整。通过实验分析，可以快速、准确地测量运动平台运动过程中的误差，能够满足精密测量的要求。

1  测量原理与系统

图1所示为运动平台的6个自由度误差。由图1可知：精密直线运动平台沿Z方向移动时，需要测量3个位移误差(△x，△y，△z)和3个角度误差(△α，△β，△γ)。其中，定位误差△z的测量技术已经成熟，可以通过传统的激光干涉仪简单而精确地测量。测量二维直线度误差(△x，△y)、二维角度误差(△α，△β)和滚转角误差△γ的敏感器件不同，其测量原理及光路也不同。

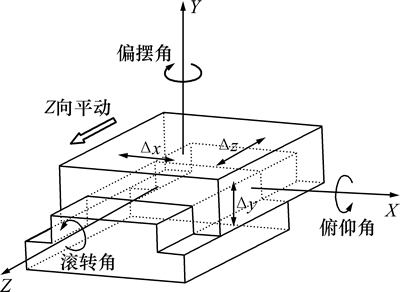
图1  运动平台的六自由度误差

Fig. 1  Six-degree-of-freedom motion errors of a motion platform

1.1  直线度和角度测量原理

二维直线度误差测量原理如图2所示。测量敏感元件是1个角锥棱镜，安装在待测的运动平台上，测量激光束入射到角锥棱镜后，反向回射，由1个四象限探测器(QD)接收。若平台运动时，在横向有△x或纵向有△y的偏移，则测量光束经过角锥棱镜回射后，在QD上就能检测到放大2倍的偏移，即

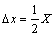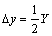；              (1)

式中：X和Y分别为QD上接收的光斑在水平和竖直方向的位移；△x和△y分别为对应方向的直线度误差。若QD的位置分辨率为0.1 μm，则直线度误差的理论分辨率能达到0.05 μm。

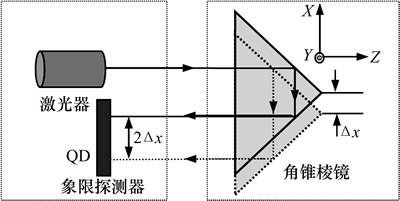
图2  直线度误差测量原理

Fig. 2  Schematic diagram for measuring straightness errors

二维角度误差的测量是以平面反射镜为敏感元件，测量原理如图3所示。敏感元件安装在待测运动平台上，测量光线通过1个固定安装的分光镜入射到反射镜上，反射回的光线经过透镜(Lens)聚焦后，由位于透镜焦平面的位置敏感探测器(PSD)接收。通过分析可知，该反射光线对运动平台的平移和滚转不敏感，而只对俯仰、偏摆敏感。当随平台一起运动的平面反射镜发生俯仰角误差△α或者偏摆误差△β时，反射光线则产生2倍的角度偏转，经透镜聚焦到PSD上像点发生相应的位移，即

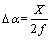；           (2)

式中：X和Y分别为PSD接收的光斑在水平、竖直方向的位移；△α和△β分别为对应方向的角度误差；f为透镜的焦距。若选择透镜焦距f=200 mm，PSD的位置分辨率为1 μm，则二维角度误差的理论分辨率为0.5″。

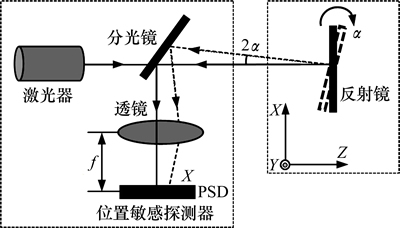
图3  俯仰角(偏摆角)误差测量原理

Fig. 3  Schematic diagram for measuring pitch and yaw errors

滚转角误差测量相对较难^[17]，本系统通过对运动平台同一水平位置上2个不同点处竖直方向的位移变化来间接测量滚转角误差。敏感器件是1个角锥棱镜组，由2个角锥反射镜并列组成，作为测量头安装在运动平台上。测量原理如图4所示，其中固定部分有1个斜方棱镜，激光器发出的测量光束通过到斜方棱镜分成两束平行光，入射到角锥棱镜后回射，由2个四象限探测器(QD1和QD2)接收。滚转角为

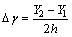               (3)

式中：Y₁和Y₂分别为QD1和QD2上接收的光斑在竖直方向的位移；△γ为滚转角误差；h为2条平行光线之间的距离。选择h=28 mm，QD位置分辨率为0.1 μm，滚转角误差测量的理论分辨率为0.4″。

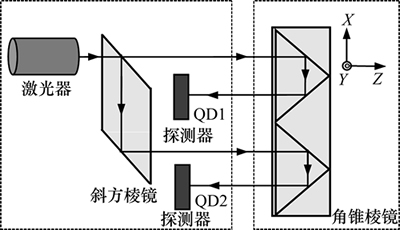
图4  滚转角误差测量原理

Fig. 4  Schematic diagram for measuring roll error using cube corner prism

1.2  五自由度误差测量系统

基于以上测量原理，图5所示为一种五自由度误差同时测量方法。测量装置由移动测头和固定部分组成。稳定的激光器发出的光线经过斜方棱镜分成2条平行光束1和2。其中，光束1射向移动部分的角锥反射镜的分光膜上，反射光束3返回到固定部分，经透镜聚焦成像后到位置敏感传感器上，获得偏摆角和俯仰角误差；透射光则由角锥反射镜镜后向回射，由四象限探测器(QD1)接收，可直接得到直线度误差。另外一光束2入射到角锥棱镜上回射后，由QD2接收，结合QD1接收的信息，差分后得到滚转角误差。

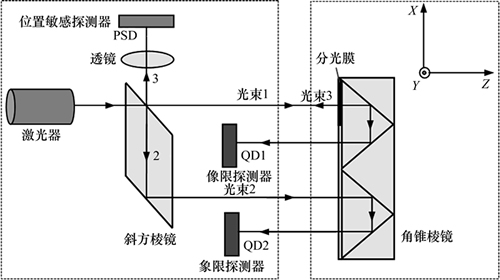
图5  五自由度误差同时测量系统示意图

Fig. 5  Schematic diagram for simultaneously measuring five-degree-of-freedom motion errors

2  实验与分析

为验证测量方法及系统的可行性与可靠性，在实验室条件下对测量系统进行标定实验、重复性实验和精度对比实验。

二维直线度和三维角度误差测量的标定都是采用英国Renishaw公司的XL80激光干涉仪系统，Renishaw XL80是机床、三次元坐标测量床及其他定位装置精度校准用的高性能仪器，能够分别测量定位精度、直线度、角度等误差项目。实验装置如图6所示，其中，中间部分是待测精密直线运动平台，上面安装有本系统的测量角锥棱镜和Renishaw XL80的角度测量反射镜，平台上左侧和右侧分别安装本系统测量的光学组件和XL80激光干涉仪的激光头及其固定的参考反射镜。当平台运动时，同时得到本系统和Renishaw XL80激光干涉仪的读数。

2.1  直线度和角度标定

Renishaw XL80激光干涉仪直线度测量范围为±2.5 mm，其直线度分辨率为0.01 μm。测量精密短行程运动平台的精度为±0.5 μm。二维直线度误差标定实验结果如图7所示，△x和△y标定范围在±70 μm进行。线性相关系数R分别为0.999 9和0.999 8，实际测量分辨率可达到0.1 μm。

Renishaw XL80激光干涉仪的偏摆角和俯仰角测量范围为±10°，分辨率为0.01″，测量精度为±0.1″。二维角度误差标定实验结果如图8所示，△α和△β标定范围在±600″进行，线性相关系数R分别为0.999 9和0.999 8，实际测量分辨率高于1″。

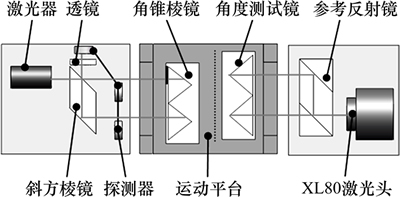
图6  实验装置

Fig. 6  Experimental setups for errors measurement

图7  直线度误差标定实验

Fig. 7  Calibration results of straightness error

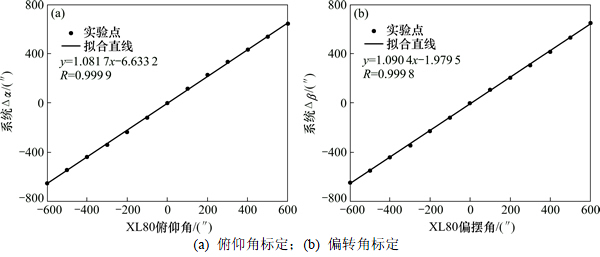
图8  俯仰角和偏摆角误差标定

Fig. 8  Calibration results of pitch and yaw errors

滚转角误差测量是通过对平台同一水平位置上2个不同点处竖直方向的位移变化来间接测量的，因此，可以同时对2个测量竖直位移的四象限探测器进行标定。标定实验结果如图9所示，滚转角△γ标定范围在±300″进行，线性相关系数为R=0.999 8，实际测量分辨率约为1″。

综合以上实验结果可以看出：二维直线度误差、二维角度及滚转角误差的测量均具有很好的示值线性，测量的分辨率与理论值相符，能够进行精密测量。

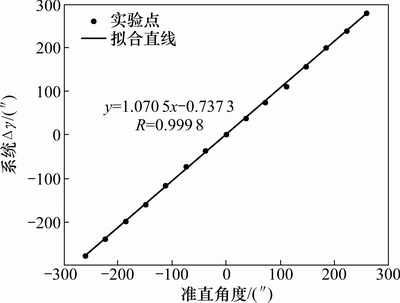
图9  滚转角误差标定实验

Fig. 9  Calibration results of roll angle error

2.2  重复性和对比实验

图10所示为系统的重复性测量实验结果(在运动平台行程13 mm测量范围内，不同时间进行3次重复特性实验，每1 mm设置为1个测量点)。其中，图10(a)所示为二维直线度X方向的实验结果，图10(b)和图10(c)所示分别为二维角度(偏摆角)和滚转角误差测量结果。由图10可以看出：系统直线度和角度误差测量的重复性良好，对应点直线度测量的偏差不大于0.5 μm，角度存在的偏差不大于4″。结合XL80激光干涉系统在同等条件下对运动平台重复性测量结果分析，认为造成偏差的主要原因是运动平台自身导轨存在的反向间隙。

图11所示为测量系统与Renishaw XL80对同一运动平台进行误差测量的对比实验结果(实验装置如图6所示)。在运动平台行程13 mm的测量范围内，每1 mm设置为1个对比测量点。图11(a)和(b)所示分别为二维直线度和二维角度的定点比对实验结果。由图11可以看出：在平台运动的范围内，系统和Renishaw XL80的测量趋势接近，直线度测量点之间偏差在0.8 μm以内，数据经过最小包容法处理后，两者测量的直线度误差相当；而偏摆角度对应点的偏差在4″以内。

从实验结果来看，在运动平台测量行程内，二维直线度、二维角度误差测量精度能够分别达到1 μm和5″，但对比测量点之间还是存在一定的偏差。经过分析，造成偏差的主要原因如下。

图10  重复性测量实验

Fig. 10  Experimental results of measurement repeatability

图11  误差测量对比实验

Fig. 11  Comparison experiment results of straightness and angle errors

1) 测量系统本身存在的误差，主要是斜方棱镜和角锥棱镜的加工误差。滚转角误差的测量要求入射的两光束严格平行，由于棱镜本身加工误差的存在，使实际的2束光不是真正的平行光，导致测量结果存在偏差。同时，角锥棱镜作为误差测量的敏感器件，存在的制造误差会导致入射光线和出射光线不是严格平行，会对测量结果产生影响。这类系统误差可以通过反复标定来减小。

2) 系统进行测量时，角锥棱镜这敏感元件随着平台导轨移动，导轨的俯仰角、偏摆角误差也会对直线度的误差产生串扰作用。考虑到测量的精密运动平台行程较小，此因素影响作用较小。

3) 用于对比测量的Renishaw XL80是单参数测量仪器，其测量镜组安装的位置及高度与本实验系统的位置及高度不一致，且测量方向是相对的，给对比实验结果的偏差造成了不可忽略的影响。

4) 外界环境引起的随机误差，主要是空气环境引起的误差和背景光对探测器的影响造成的误差。

3  结论

1) 提出一种基于激光准直技术的五自由度运动误差同时测量方法。仅以1个角锥棱镜作为敏感器件，1次安装就能够同时测量直线运动平台2个直线度误差和3个角度误差。测量系统结构简单，调节灵活方便，测量头体积较小，无电缆连接，适用于精密运动平台多自由度误差同时测量。

2) 系统具有良好的重复性和稳定性，测量直线度误差的分辨率高于0.1 μm，角度误差的分辨率优于1″，直线度、角度误差测量精度分别达到1 μm和5″。该方法能够快速、准确地测量直线运动平台5项误差，对定位平台的位置和姿态调整具有重要意义。

参考文献：

[1] 阳波, 段吉安. 光电子封装超精密运动平台末端姿态调整[J]. 中南大学学报(自然科学版), 2011, 42(5): 1290-1295.

YANG Bo, DUAN Jian. Opto-electronics packaging platform for ultra-precision position and attitude adjustment[J]. Journal of Central South University (Science and Technology), 2011, 42(5): 1290-1295.

[2] MENQ C H, ZHANG Jihua, SHI Jian. Design and development of an interferometer with improved angular tolerance and its application to x–y theta measurement[J]. Review of Scientific Instruments, 2000, 71(12): 4633-4638.

[3] ZHANG Caini, WANG Xiangzhao. Sinusoidal phase-modulating laser diode interferometer for measuring angular displacement[J]. Optical Engineering, 2004, 43(12): 3008-3013.

[4] GAO Wei, ARAI Y, SHIBUYA A, et al. Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage[J]. Precision Engineering, 2006, 30(1): 96-103.

[5] KIM J A, BAE E W, KIM S H, et al. Design methods for six-degree-of-freedom displacement measurement systems using cooperative targets[J]. Precision Engineering, 2002, 26(1): 99-104.

[6] LIU C H, JYWE W Y, CHEN C K. Development of a simple system for the simultaneous measurement of pitch, yaw and roll angular errors of a linear stage[J]. The International Journal of Advanced Manufacturing Technology, 2005, 26(7/8): 808-813.

[7] HUANG H L, LIU C H, JYWE W Y, et al. Development of a DVD pickup-based four-degrees-of-freedom motion error measuring system for a single-axis linear moving platform[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2010, 224(1): 37-50.

[8] FAN K C, CHEN M J, HUANG W M. A six-degree-of-freedom measurement system for the motion accuracy of linear stages[J]. International Journal of Machine Tools and Manufacture, 1998, 38(3): 155-164.

[9] 杨振, 李广云, 贺磊. 光学准直测量方法与精度分析[J]. 红外与激光工程, 2011, 40(2): 282-286.

YANG Zhen, LI Guangyun, HE Lei. Measurement methods and precision analysis of optical collimation[J].Infrared and Laser Engineering, 2011, 40(2): 282-286.

[10] 王宪, 谭建平, 陈国强, 等. 基于主动视觉的测量装置精度校准方法[J]. 中南大学学报(自然科学版), 2014, 45(4): 1072-1076.

WANG Xian, TAN Jianping, CHEN Guoqiang. Active vision-based accuracy calibration technology for measurement devices[J]. Journal of Central South University (Science and Technology), 2014, 45(4): 1072-1076.

[11] 吕勇, 冯其波, 刘立双, 等. 基于多准直光的六自由度测量方法[J]. 红外与激光工程, 2014, 43(11): 3597-3602.

L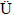 Yong, FENG Qibo, LIU Lishuan, et al. Six-degree-of-freedom measurement method based on multiple collimated beams[J]. Infrared and Laser Engineering, 2014, 43(11): 3597-3602.

[12] FAN K C, CHEN M J. A 6-degree-of-freedom measurement system for the accuracy of X-Y stages[J]. Precision Engineering, 2000, 24(1): 15-23.

[13] FAN K C, CHU C L, LIAO J L, et al. Development of a high-precision straightness measuring system with DVD pick-up head[J]. Measurement Science and Technology, 2003, 14(1): 37-50.

[14] LIU C H, JYWE W Y, HSU C C, et al. Development of a laser-based high-precision six-degrees-of-freedom motion errors measuring system for linear stage[J]. Review of Scientific Instruments, 2005, 76(5): 055110.1-055110.6.

[15] FENG Qibo, ZHANG Bin, KUANG Cuifang. Four Degree-of-Freedom Geometric Error Measurement System with Common-Path Compensation for Laser Beam Drift[J]. International Journal of Precision Engineering and Manufacturing, 2008, 9(4): 26-31.

[16] FENG Qibo, ZHANG Bin, CUI Cunxing, et al. Development of a simple system for simultaneously measuring 6DOF geometric motion errors of a linear guide[J]. Optics Express, 2013, 21(22): 25805-25819.

[17] 马军山, 王向朝, 房祖捷 滚转角误差的光学精密测量技术研究[J]. 光学学报, 2000, 20(10): 1403-1406.

MA Junshan, WANG Xiangzhao, FANG Zujie. Optical precision measurement technique of rolling error[J]. Acta Optica Sinica, 2000, 20(10): 1403-1406.

(编辑  杨幼平)

收稿日期：2016-10-07；修回日期：2016-12-19

基金项目(Foundation item)：国家自然科学基金资助项目(51475479)；国家高新技术研究发展计划(863计划)项目(2012AA040406)；湖南省自然科学基金资助项目(14JJ2010)；浙江大学流体动力与机电系统国家重点实验室开放基金资助项目(ZKF-201401) (Project (51475479) supported by the National Natural Science Foundation of China; Project (2012AA040406) supported by the National High-Tech R&D Program of China; Project (14JJ2010) supported by the Natural Science Foundation of Hunan Province, China; Project (ZKF-201401) supported by the Open Project of Stage Key Laboratory of Fluid Power Transmission and Control, Zhejiang University)

通信作者：郑煜，博士，副教授，从事集成光子器件封装制造理论与技术研究；E-mail：zhengyu@csu.edu.cn