一种考虑异常中断的导航星座星间链路路由改进算法
王东会,刘文祥,唐小妹,黄仰博
(国防科学技术大学 电子科学与工程学院卫星导航研发中心,湖南 长沙,410073)
摘要:为解决导航星座星间链路异常中断时的路由问题,提出一种考虑链路异常状态的路由改进算法。通过导航星座特有的星间测距信息进行链路异常检测与识别,根据检测出的链路异常状态对K短路径路由算法进行改进。对改进算法与K短路径算法及泛洪策略进行比较分析,研究结果表明:在处理链路异常中断时,改进算法比泛洪策略增加的额外链路负担更小,时效性更高;而在链路传输时延及链路切换次数上改进算法与K短路径算法相当。
关键词:导航星间链路;异常中断;星间测距;K短路径算法;泛洪策略
中图分类号:TN967.1 文献标志码:A 文章编号:1672-7207(2014)03-0762-07
Improvement of navigation inter-satellite link routing algorithm considering abnormal link disruption
WANG Donghui, LIU Wenxiang, TANG Xiaomei, HUANG Yangbo
(Satellite Navigation Research and Development Center, National University of Defense Technology,
Changsha 410073, China)
Abstract: To solve the routing problem of navigation inter-satellite link under abnormal link disruption conditions, an improved routing algorithm was proposed. Inter-satellite ranging was adopted for link abnormity detection and identification, and K shortest paths algorithm was improved by adding link abnormity status. Comparison simulation analysis between the improved algorithm and K shortest paths adding flood method was given. Results show that the additional link cost of the improved algorithm is much less than that of the flood method when the abnormal link disruption is solved, and in the aspects of link transmission delay and switch number, the improved algorithm and K shortest paths show little difference.
Key words: navigation inter-satellite link; abnormal link disruption; inter-satellite ranging; K shortest paths algorithm; flood method
与通信星座星间链路相比,导航星座星间链路具有很多不同的特点。通信星座的星间链路偏重于进行大容量远距离的通信信息传输,而导航星座星间链路兼具星间测距及星间通信功能[1-2],星座可实现自主导航[3]。导航星座星间链路通信速率较低,因此,链路拥塞、排队处理等通信星座星间链路中关注的问题并不是导航星座星间链路的研究重点。目前,国内外学者对导航星座星间链路的研究主要集中在自主导航算法以及星座设计等方面[4-6],而对路由技术的研究较少。导航星座路由技术的研究主要围绕K短路径算法展开,主要的研究成果有基于Walker星座的K短路径算法[7]以及最短路径与K短路径的折中优化算法[8]等。这些算法都是将链路时延及切换次数等常规性能作为路由计算依据,未考虑链路异常状态,无法处理链路异常中断的情况。通信星座星间链路通常采用洪泛策略来处理链路异常中断时的路由问题[9],但此方法往往在正常通信链路中断时方才启动,时效性不高,而且需要大范围的遍历数据传输,不仅增加链路状态控制的复杂性,也增加链路负担,不适用于低信息速率的导航星座星间链路系统。
在上述研究成果的基础上,针对导航星座星间链路的特点,本文作者提出一种考虑链路异常状态的路由改进算法。改进算法通过导航星座特有的星间测距信息进行链路异常检测与识别,根据链路异常状态对K短路径算法的权值生成及链路选择方法进行改进,首先论述导航星间链路可视性及建链模型。然后,对K短路径算法及泛洪策略进行介绍。重点论述链路异常检测与识别的算法原理以及K短路径算法的改进方法。最后,采用仿真实验对比分析改进算法与K短路径算法及泛洪策略在链路发生异常中断时的星间通信性能。
1 导航星座星间可视性及建链模型
导航星座星间链路兼具星间测距及星间通信功能,星间链路工作体制通常为时分多址[6]。将星座周期分为若干时隙,每颗卫星占据1个时隙,在各自的时隙中进行测距及通信。由于卫星运动具有周期性和可确定性,因此,每个时刻的卫星建链表可事先在地面计算并存储在卫星中,整个星座依据每个时刻的固定建链表组建星间链路。
导航卫星间的空间几何位置关系如图1所示。
2颗卫星可建立星间链路的条件如下:

图1 卫星间的相对位置关系
Fig. 1 Space geometry relationship between satellites and earth
(1) 2颗卫星的视线矢量不被地球遮挡且不穿过电离层;
(2) 2颗卫星的视线矢量分别处于2颗卫星天线波束角度覆盖范围内。
星间建链数学模型如下。
假设卫星S1的惯性系位置矢量为r1,卫星S2的惯性系位置矢量为r2,地心惯性系位置矢量为O,地球半径为R,则有如下关系:
 (1)
(1)
 (2)
(2)
 (3)
(3)
假设电离层高度为hI,星间链路天线仰角取值范围为(γ1, γ2),则建链判决条件如下。
当2颗卫星满足如下式时,2颗卫星可建链。
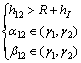 (4)
(4)
根据上述数学模型,可知图1中卫星S1与S2可建立星间链路,而卫星S1与S3由于地球遮挡而不可建立星间链路。
2 K短路径路由算法及泛洪策略
2.1 K短路径路由算法
Dijkstra最短路径算法是通信卫星网络和导航卫星网络普遍采用的路由算法。该算法以总的路径时延最短为准则进行路由计算。某条链路P(S1→S2→Sn)的总的路径权值计算方法如下:
 (5)
(5)
其中:τ(Si→Si+1)为2颗卫星间的信号传输时延。选择总时延最小的路径作为最优路径。
K短路径算法在最短路径算法的基础上进行改进,按照式(5)计算出最短路径,次短路径以及第三短路径等多条备选路径。根据应用场合的不同,最优的路径选择要综合考虑链路生存时间、链路切换次数、排队等待时延以及链路开销等多种不同因素[9-12]。
在导航星座星间链路路由计算中,除链路时延外,主要考虑链路的切换次数及剩余时间[8]。
2.2 泛洪策略
通信卫星网络通常采用K短路径与泛洪策略相结合的方法处理链路异常中断。过程如下[9]:
(1) 根据K短路径算法计算出的最优路由进行数据传输,如果起始卫星S1的最优下一跳卫星节点通信中断,则启动泛洪过程;
(2) 起始卫星S1向所有邻接节点卫星Si发送泛洪数据包;
(3) 邻接节点Si收到泛洪数据包后查询路由表,若当前时刻经过路由转发成功,则发送成功应答信息回到卫星S1,否则邻接节点Si启动泛洪路由过程,继续向下一级邻接节点发送泛洪数据包。
(4) 当起始卫星S1收到第一条成功应答信息时就完成了泛洪过程。
从上述过程可知,采用泛洪策略处理链路异常中断实际上是一种遍历搜索过程,所需传输的数据量较大。在正常链路无法传输时才启动泛洪,时效性不高。
3 考虑链路异常中断的路由改进算法
根据导航星座星间链路的特点,本文作者提出一种考虑链路异常中断的路由改进算法。算法在2个方面进行了改进:一是增加链路异常中断检测与识别方法;二是根据链路异常状态对K短路径路由算法的权值生成方法以及链路选择方法进行改进。
3.1 链路异常中断检测与识别算法
导航星座可通过星间测距进行自主定轨,从而实现星座的自主运行。为实现星上的自主导航解算,所有卫星星间测距结束后,需要通过星间通信链路进行测距值回传。这给通信异常中断的检测和识别提供新的手段。
每颗导航卫星均维持1个测距表及1个路由表。测距表记录每个测距时刻与该卫星建立链路的卫星号,路由表维持该卫星任意时刻路由状态。由于卫星运动具有周期性及可预测性,因此,这2个表都可以事先由地面计算,并存储于卫星的存储器中。在某个测距时刻,卫星按照测距表与相应卫星进行配对测距。所有卫星测距结束后,统一进行测距值的星间传输。测距值的传输原则为所有卫星将自身的测距值按照发射卫星号进行回传,这样就确保所有卫星都可获得其它卫星对自己的测距值。星间双向测距条件下可保证可测距的卫星两两间均可获得对方的测距回传值。卫星Si的星间测距及测距值回传示意图如图2所示。

图2 星间测距及测距值传输
Fig. 2 Inter-satellite ranging and ranges transmission
假设每颗卫星具有m个独立的星间天线,每个星间天线对准1颗卫星,每个时刻的天线对准关系事先由地面计算。在1个测距周期内,任意卫星Si的每个天线均可进行k次测距(发射k次测距信号),并接收k次反向测距信号(星间采用双向测距)。测距结束并进行测距值回传后,卫星Si可获得测距集合Pi={P1, P2, …, Pn},其对应的测距卫星集合为AiP={S1, S2, …, Sn},此集合与卫星Si的测距表Ti是一一对应的,若某颗卫星故障导致通信链路异常中断时,测距将无法完成回传,则集合AiP中的元素将少于测距表Ti中的元素。通过对比2个集合元素即可检测出当前通信中断的链路,检测方法如下式所示:
 (6)
(6)
然而,根据式(5)仅仅只能检测出2颗卫星间的通信链路发生中断,但无法进一步识别具体故障卫星,更无法识别具体的故障天线。
为进行更进一步的故障识别,首先对每颗卫星的中断链路集合Ei进行适当修改,增加当前出现故障时的收发两端天线编号,如下式所示:
 (7)
(7)
其中:a表示发射信号卫星Si使用的天线编号;b表示接收信号卫星Sj使用的天线编号。
显然,仅根据单颗卫星的测距回传值无法分离故障发生在发射端卫星还是接收端卫星,更无法定位故障天线,因此,要想进行故障识别,需要在所有测距卫星之间传输集合Eis。卫星根据自身的故障集合以及收到的测距卫星故障集合进行综合评判,故障识别方法如下。
首先,将自身及收到的故障集合元素合并,保留共有元素个数,得到总的故障集合,如下式所示:
 (8)
(8)
当某颗卫星Si的某个天线a发生信号收发故障时,卫星Si的故障集合及与其进行配对测距卫星的故障集合均存在元素Sia。由于每个周期卫星发射k次测距信号并接收k次反向测距信号,因此,故障卫星天线将出现2k次,即满足如下条件:
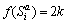 (9)
(9)
式(9)表示集合EA中元素Sia的个数为2k,f定义为在集合EA中取元素个数的函数。
因此,可根据式(8)进行故障识别,判断条件如下:
(1) 若集合EA为空,则表明星间通信无中断;否则,判定为有中断;
(2) EA非空时,寻找集合中个数等于2k的元素,此元素对应的天线即为故障天线。
故障识别后可得到卫星状态因子如下:
 (10)
(10)
3.2 K短路径路由算法改进
星间链路异常中断检测结束后,对整个星座的链路状态信息进行实时更新。当星间链路需要执行上注信息或遥测遥控信息传输等星间通信任务时,根据当前的链路状态实时进行路由计算,寻找最优传输路径。
根据卫星状态因子对式(5)的权值计算方法进行改进,得到新的权值计算方法如下:
 (11)
(11)
其中:σia为式(10)中的卫星状态因子。
式(11)表示在原路径权值的基础上乘以链路上各节点卫星对应天线的状态。
改进后的最优路由选择准则定义为:
(1) 根据式(11)计算2个目标卫星间的所有链路权值并找出所有权值非0的组合,在这个组合中按照权值从小到大排序,选出前K个备选路径;
(2) 判断上一次选择的路径在本次是否存在,若存在,则优先选中;
(3) 若K条备选路径中均无上一次选中链路,则选择时延最短的链路;
(4) 计算备选链路的剩余生存时间,剩余生存时间越多,被选中的概率越高。
4 算例分析
4.1 仿真条件及场景
采用标准型Walker 24/3/2 MEO导航星座进行算法仿真分析,卫星高度为24 000 km,轨道倾角为55°,星间采用4个窄波束天线[13],天线仰角扫描范围假设为20°~60°。电离层高度H取为1 000 km[8]。利用美国AGI公司的STK软件创建星座场景[14]。仿真起始时间为2008年7月1日12:00,仿真时间长度为1个星座周期约15 h,数据采样点间隔为1 min。
按照第1节星间可视性模型及上述仿真条件,以MEO1卫星为例,给出星座其它卫星对MEO1的星间可视性仿真结果如图3所示。图3中线条表示横坐标对应的时刻MEO1与纵坐标对应的卫星相互可视。从图3可以得出:与卫星MEO1永久可视的卫星集合为{MEO2, MEO3, MEO7, MEO8, MEO13, MEO16, MEO19, MEO24}。类似地,所有24颗卫星均可得到自己的永久可视卫星集合[15]。

图3 MEO1星间可视性结果
Fig. 3 MEO1 inter-satellite visibility
在上述星间可视条件下,考虑如图4和图5所示的2种建链结构,每个拓扑网络中每颗卫星可建立4条链路和2个拓扑共8条链路,均为永久可视卫星建链。
按照上述星间建链方式,模拟3个异常场景,分别如下。
(1) 场景1:假设MEO12第1个天线故障,即拓扑结构1中MEO12与MEO13之间的链路中断,拓扑结构2中MEO12与MEO14之间的链路中断。

图4 星间建链拓扑1
Fig. 4 ISL topology 1
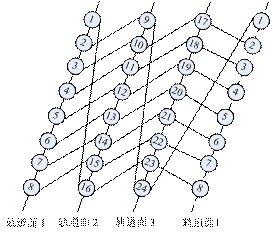
图5 星间建链拓扑2
Fig. 5 ISL topology 2
(2) 场景2:假设MEO13的4个天线均故障,与其连接的8条链路中断。
(3) 场景3:假设MEO2及MEO19卫星各自的4个天线均故障。
4.2 仿真结果
针对上述3个场景进行仿真分析。首先根据建链策略及式(7)~(9)给出3个场景故障集合仿真结果。对EA中所有元素按出现次数进行统计,结果如表1所示。
由于仿真场景中每个卫星天线可测距2次(2个测距拓扑),因此根据式(9)可知异常检测门限为4,即如果异常集合数组中存在个数为4的元素,则判定其为故障。因此,可根据表1得到检测结果如下:场景1的12号卫星天线1出现故障;场景2的13号卫星4个天线出现完全故障;场景3的2号及19号卫星4个天线出现完全故障。此结果与实验设定完全相同,可见本文故障检测识别方法可正确检测出星间故障,并可将故障定位到具体的卫星天线。
表1 故障集合EA元素出现次数统计结果
Table 1 Statistical results of element number in abnormity array EA

以MEO13故障的场景2为例,对比分析本文算法与K短路径算法及泛洪策略在链路时延、链路额外负担以及链路切换次数等方面的性能。
以卫星MEO1为例,仿真分析MEO1到其他23颗卫星的最大路径传输时延。分别给出有故障条件下本文算法与K短路径及泛洪策略链路时延比较结果,以及正常无故障条件下K短路径算法与有故障条件下本文算法链路时延比较结果,分别图6和图7所示。

图6 故障条件下本文算法与K短路径加泛洪方法的最大路径传输时延比较
Fig. 6 Comparison of transmission delay between improved algorithm and K shortest paths added flooding method under abnormal condition

图7 无故障条件下K短路径算法与有故障条件下本文算法的最大路径传输时延比较
Fig. 7 Comparison of transmission delay between K shortest paths under normal condition and improved algorithm under abnormal link conditions
图6和图7中时延为0表示MEO13卫星无法通信。当MEO13故障时,由于MEO11、MEO12、MEO14需要MEO13卫星中转,因此,也受到影响,无法按照K短路径计算出的链路进行正常通信。由图6可见:采用K短路径加泛洪策略完成上述3颗受影响卫星的星间通信时,链路时延明显大于本文算法。主要原因是K短路径算法与泛洪策略结合进行异常处理时,只对故障链路局部进行遍历,而本文算法是事先对整个链路进行全局优化,而且泛洪策略还需要进行信息回传以确认目标节点成功收到通信信息。而从图7可见:本文算法处理上述3颗受影响卫星时,链路时延与正常无故障时的K短路径算法相比最多仅增加63.9 ms,其余卫星传输链路时延不变。因此,可以认为本文算法在链路时延性能上与K短路径算法的相当。在处理链路异常中断时,时延性能比K短路径加泛洪方法的优。
在额外增加的链路负担方面,为完成上述3颗卫星的通信,泛洪策略需要进行434次两两卫星之间的泛洪数据传递。而本文算法只需额外传输卫星故障集合,整个星座完成1次故障检测只需进行192次两星间的数据传递,而且故障集合的数据量远远小于泛洪数据包的数据量。因此,从额外增加的链路负担角度,本文算法显然拥有更高的性能。
由于本文算法主要对备选路径的选择进行优化,最终路径的确定准则与K短路径算法相同,因此,可以推断出2种算法在链路切换次数上的性能是相当的。仿真实验验证此推论,这里不再列出具体结果。
5 结论
(1) 可通过故障检测与识别将链路中断的故障具体定位在卫星的某个天线。
(2) 在星间通信之前完成链路中断检测与识别。在路由计算时根据链路异常状态进行全局优化,选择最优传输路径,时效性较高。
(3) 增加的额外链路负担较小,只需要额外在测距卫星之间两两传输卫星故障集合,传输距离只有1跳,不需卫星中转,传输数据量也很小。改进算法在链路传输时延、链路切换次数等性能上与K短路径算法相当。与K短路径加泛洪策略的星间异常中断处理机制相比,改进算法额外增加的链路负担更小,时效性更高。
参考文献:
[1] Francisco A F. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data[J]. Advances in Space Research, 2011, 47(5): 786-801.
[2] Sanchez M, Pulido J A. The ESA “GNSS+” Project Inter-satellite ranging and communication links in the frame of the GNSS infrastrcture evolutions[C]// ION GNSS, Savannah. GA, 2008: 2538-2546.
[3] Eissfeller B, Zink T. Autonomous satellite state determination by use of two-directional links[J]. Int J Satellite Commun, 2000, 18(4/5): 325-346.
[4] ZOU Decai, LU Xiaochun, WU Haitao, et al. Research on global navigation satellite system (GNSS) autonomous navigation technology based on inter satellite links (ISL)[C]// ION GNSS, Savannah. GA, 2009: 1288-1297.
[5] John A R, Matthew O, Paul W. On-orbit validation of GPS IIR autonomous navigation[C]// ION 59th Annual Meeting of The Institute of Navigation and CIGTF 22nd Guidance Test Symposium. Albuquerque, NM, 2003: 411-419.
[6] Rajan J A. Highlights of GPS II-R autonomous navigation[C]// ION 58th Annual Meeting of The Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque, NM, 2002: 354-363.
[7] 何家富, 姜勇, 张更新, 等. 一种具有异轨星间链路的Walker星座网络拓扑与路由生成方案[J]. 解放军理工大学学报(自然科学版), 2009, 10(5): 409-413.
HE Jiafu, JIANG Yong, ZHANG Gengxin, at el. Topology and route production scenario of walker satellite constellation network with inter-satellite link[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2009, 10(5): 409-413.
[8] 周建华, 杨龙, 徐波, 等. 考虑波束限制的改进导航星座星间链路方案[J]. 中国科学: 物理学 力学 天文学, 2011, 41(5): 575-580.
ZHOU Jianhua, YANG Long, XU Bo, at el. An improved satellite link scheme with beam restriction for the navigation constellation[J]. Sci Sin Phys Meth Astron, 2011, 41(5): 578-580.
[9] 郭炎鑫, 郑刚. 多层卫星网络链路中断容忍路由策略设计[J].电子与信息学报, 2010, 32(8): 1892-1897.
GUO Yanxin, ZHENG Gang. Design of a link disruption tolerant routing strategy in multilayered satellite network[J]. Journal of Electronics & Information Technology, 2010, 32(8): 1892-1897.
[10] 苑喆, 张军, 柳重堪. LEO/MEO双层卫星网的分层动态路由算法[J]. 北京航空航天大学学报, 2006, 32(7): 788-792.
YUAN Zhe, ZHANG Jun, LIU Zhongkan. Dynamic routing algorithm for LEO/MEO double-layered satellite networks[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(7): 788-792.
[11] Eppstein D. Finding the K shortest paths[J]. SIAM J Computing, 1998, 28(2): 652-673.
[12] XU Wangtu, HE Shiwei, SONG Rui, et al. Finding the K shortest paths in a schedule-based transmit network[J]. Computer & Operations Research, 2012, 39(8): 1812-1826.
[13] 徐勇, 常青, 于志坚. GNSS星间链路测试与通信新方法研究[J]. 中国科学: 技术科学, 2012, 42(2): 230-240.
XU Yong, CHANG Qing, YU Zhijian. On new measurement and communication techniques of GNSS inter-satellite links[J]. Sci China Tech Sci, 2012, 42(2): 230-240.
[14] 刘亚琼, 杨旭海. GPS星间链路及其数据的模拟方法研究[J]. 时间频率学报, 2010, 33(1): 39-46.
LIU Yaqiong, YANG Xuhai. GPS inter-satellite link and simulation of ISL data[J]. Journal of Time and Frequency, 2010, 33(1): 39-46.
[15] 王振永, 王平, 顾学迈, 等. 卫星网络中永久星间链路的设计方法研究[J]. 通信学报, 2006, 27(8): 129-133.
WANG Zhenyong, WANG Ping, GU Xuemai, et al. Research on design of permanent inter-satellite-links in satellite networks[J]. Journal on Communications, 2006, 27(8): 129-133.
(编辑 邓履翔)
收稿日期:2013-05-07;修回日期:2013-07-21
基金项目:教育部新世纪优秀人才支持计划项目(NCET-08-0144)
通信作者:王东会(1985-),男,黑龙江齐齐哈尔人,博士研究生,从事卫星导航应用的研究;电话:13873124464;E-mail: wdhhawk@163.com