DOI： 10.11817/j.issn.1672-7207.2019.09.006

螺栓固结界面接触刚度的虚拟材料建模

肖会芳¹,孙韵韵¹,徐金梧¹,邵毅敏²

（1. 北京科技大学 机械工程学院，北京，100083；

2. 重庆大学 机械传动国家重点实验室，重庆，400044）

摘要:提出一种基于统计学模型的粗糙接触界面虚拟材料建模方法，将螺栓固结界面等效为局部的虚拟材料，虚拟材料与两侧接触基体固定连接。基于螺栓固结界面粗糙形貌的Greenwood-Williamson统计学模型描述，推导虚拟材料的弹性模量、泊松比、密度和厚度等材料参数的解析表达式，建立虚拟材料的材料参数与粗糙界面属性参数之间的关系式，分析螺栓固结界面的表面粗糙形貌、基体材料属性对虚拟材料的材料参数和界面接触刚度的影响特性。采用模态实验测试和基于虚拟材料的有限元仿真分析方法，验证粗糙接触界面虚拟材料建模方法的准确性。研究结果表明：虚拟材料的材料参数与法向载荷、界面粗糙度和接触基体弹性模量相关：随法向载荷和基体弹性模量的增加，虚拟材料的弹性模量增大，泊松比和厚度减少；随界面粗糙度的增加，弹性模量和泊松比减少，而厚度增大。螺栓固结界面接触刚度随法向载荷增大而递增，随界面粗糙增大而减小。

关键词:螺栓联接；固结界面；虚拟材料；接触刚度

中图分类号:TH11    文献标志码:A     文章编号:1672-7207（2019）09-2100-09

Virtual material based modeling for contact stiffness characteristics of bolted joint interface

XIAO　Huifang¹, SUN　Yunyun¹, XU　Jinwu¹, SHAO　Yimin²

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083,China；

2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

Abstract: Avirtual material modeling method of rough contact interface based on the statistical model was proposed in which the bolted joint interface was equivalent to a layer of virtual material and rigidly connected with the contact bodies. Based on the Greenwood-Williamson statistical model of the rough interface, the analytical expressions of elastic modulus, Poisson’s ratio, density and thickness of the virtual material were derived. The relationship between the virtual material parameters and the surface properties was established. Effects of surface roughness and material property of contact body on the virtual material parameters as well as the interfacial contact stiffness were investigated. Modal experiment measurements and finite element analysis incorporating virtual material for a bolted joint structure were performed to validate the accuracy of the modeling method. The results show that the material parameters of virtual material are dependent on the normal load, surface roughness and matrix elastic modulus. With the increase of normal load and matrix elastic modulus, the elastic modulus of virtual material increases, and the Poisson’s ratio and thickness decrease; with the increase of interface roughness, the elastic modulus and Poisson’s ratio decrease, while the thickness increases. The contact stiffness of bolted joint interface increases with the increase of normal load and decreases with the increase of interface roughness.

Key words: bolted joint; jointed interface; virtual material; contact stiffness

螺栓联接是工程结构中最常见的连接形式之一。通过螺栓将不同的工作部件连接在一起，形成整体的机器结构，广泛应用于航空航天装备、高精度制造装备、精密仪器等机械装备^[1-4]。各种类型复杂多样的螺栓联接结构的共性特征是相互接触的构件表面具有粗糙形貌，同时界面在一定预紧力下工作。螺栓固结界面的接触刚度是描述螺栓结构界面特性最重要的参数之一。研究表明，螺栓固结结构界面的接触刚度占机械结构总刚度的60%~80%，其变化直接影响界面以及机械装备系统的动力学性能^[5-8]，因此，螺栓固结界面的准确动力学建模和接触刚度的准确计算，对机械结构系统的性能分析与预测至关重要。目前，人们对螺栓固结结构的动力学建模和界面刚度特性进行了大量的研究。研究人员提出了弹簧-阻尼单元模型、接触单元模型和虚拟材料模型的建模方法，来表征和描述螺栓固结界面的接触特性^[9-15]。其中，弹簧-阻尼单元模型采用相互独立的离散弹簧-阻尼单元来表征螺栓固结界面的接触特性与动力学行为；接触单元建模方法采用零厚度单元、平面单元或三维单元来等效模拟螺栓固结界面的接触特性。弹簧-阻尼单元模型和接触单元模型存在无法描述实际连续的接触界面之间的相互耦合作用关系、建模精度不高、难以准确表征实际螺栓界面的接触特征，以及界面参数难以准确设置等缺点^[9-10]。虚拟材料建模方法通过在固结界面之间加入一层具有一定属性参数的虚拟材料来等效接触界面的接触特性，获得了广泛的关注。例如，田红亮等^[11]假设螺栓结合部是各向同性虚拟材料，并基于粗糙表面形貌的分形接触理论推导了材料参数。李小彭等^[12]以组合梁为研究对象，将结合面等效为广义间隙，利用结合面接触刚度的分形模型与材料应变能等效的方法，获得了结合面广义间隙的材料常数。孙清超等^[13]考虑结合面的压力分布不均匀性，提出了一种基于梯度虚拟材料的栓接结合面连接参数表征模型。但是，上述基于虚拟材料的结合面建模方法均是基于表面粗糙形貌的分形模型描述和Majumdar-Bhushan分形接触模型。对Majumdar-Bhushan接触模型，微凸体的变形过程是先塑性变形，再弹塑性变形，最后是纯弹性变形^[14]。这与经典接触理论和材料本构关系中接触变形是先弹性变形后塑性变形的变形过程相矛盾^[15-16]。同时，上述模型中均假设虚拟材料层的厚度为某一固定值，而不随接触界面的粗糙度而变化，不能准确表征界面粗糙度变化引起的虚拟材料厚度变化及对界面接触刚度的影响。本文作者考虑粗糙界面的弹性变形特征，基于粗糙表面形貌的Greenwood-Williamson统计学模型描述，提出一种基于统计学模型的虚拟材料建模方法，推导虚拟材料的弹性模量、泊松比、密度和厚度等材料参数的解析表达式，建立虚拟材料的材料参数与粗糙界面属性参数之间的关系式，分析螺栓固结界面的表面粗糙形貌、基体材料属性对虚拟材料的材料参数和界面接触刚度的影响特性，并采用有限元仿真和实验测试方法，验证虚拟材料建模方法的准确性。由于实际机械结构的接触界面通常承受周期性载荷的加载-卸载作用，界面粗糙微凸体的塑性变形被初始的加载-卸载作用消除，稳定工况时，界面工作在弹性接触状态，例如，GONZALEZ-VALADEZ等^[17]研究发现11次加载-卸载过程可以消除界面的塑性变形。因此，本文的粗糙界面法向接触刚度计算模型仅考虑粗糙界面的弹性变形和弹性接触刚度。

1 螺栓固结界面的虚拟材料模型

1.1　模型描述

具有粗糙表面形貌的2个构件通过螺栓连接实现固结，其粗糙界面接触模型示意图如图1(a)所示。图1(a)中，在螺栓预紧力P的作用下，表面均线距离为h的两粗糙表面相互接触；E₁和E₂分别为构件1和构件2的弹性模量；v₁和v₂分别为构件1和构件2的泊松比；G₁和G₂分别为构件1和构件2的剪切模量。图1(a)所示的双粗糙表面接触可采用图1(b)所示的粗糙表面-刚性平面接触模型进行等效。其中，等效弹性模量1/E=(1-v₁²)/E₁+(1-v₂²)/E₂，等效剪切模量1/G=(2-v₁)/G₁+(2-v₂)/G₂，等效表面粗糙形貌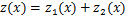，粗糙面均线与刚性平面之间的距离为h。粗糙表面与刚性平面的接触特性可以采用虚拟材料层进行表征，如图1(c)所示，其中，h为虚拟材料层的厚度；E₀为弹性模量；v₀为泊松比；ρ₀为密度。虚拟材料与接触基体和刚性平面刚性连接，实现位移与载荷的连续传递。

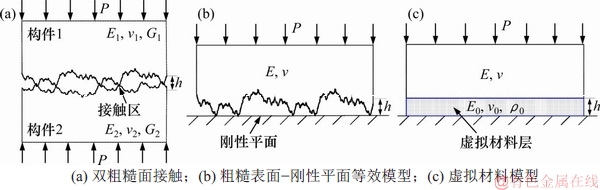
图1　粗糙界面的接触模型示意图

Fig. 1　Schematic of rough surface contact model

1.2　接触刚度

当粗糙接触界面采用虚拟材料层进行表征时，由法向载荷所做的虚功为^[11]

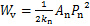(1)

式中：P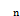为单位面积上的法向载荷；A_n为名义接触面积；k_n为单位面积上的法向接触刚度。

弹性接触体的法向应变能可以表示为

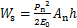(2)

法向应变能与虚功相等，故界面单位面积上的法向接触刚度可以表示为

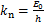(3)

2 虚拟材料参数的解析表达式

2.1　弹性模量

图1(b)所示的粗糙表面-刚性平面接触采用Greenwood-Williamson统计模型(GW模型)^[18]进行描述。其中，表面粗糙体的形状为球体且各粗糙体的曲率半径均为β，粗糙微凸体的高度符合高斯分布，其高度的标准偏差为σ_s，微凸体的面密度(单位面积上的微凸体数量)为n，各粗糙体与刚性平面的接触符合Hertzian弹性接触理论且粗糙体之间无相互作用。

单个微凸体与刚性平面接触示意图如图2所示。

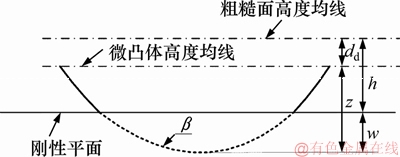
图2　单个微凸体与刚性平面接触示意图

Fig. 2　Geometry of single asperity contact

根据Hertzian弹性接触理论，其弹性接触力可以表示为^[18]

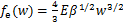(4)

式中：E为接触界面的等效弹性模量；w为弹性变形量，

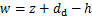(5)

z为单个微凸体的高度，定义为微凸体顶点与微凸体高度均线间的距离；d_d为微凸体均线与粗糙面均线之间的距离，d_d=1.15σ_s^[19]。

接触面积可以表示为

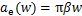(6)

考虑到单个微凸体的法向应变ε=w/β，则单个微凸体的法向接触压力可以表示为

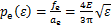(7)

单个微凸体的弹性模量可以表示为

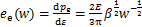(8)

采用Greenwood-Williamson统计模型(GW模型)计算粗糙界面上接触微凸体的数量，并将单个微凸体的弹性模量对微凸体数量进行积分，获得虚拟材料层的弹性模量。引入量纲一的参数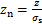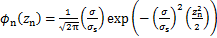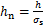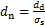：，，，，则虚拟材料层的法向接触载荷和弹性模量可以表示为

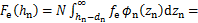
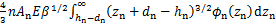(9)

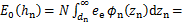
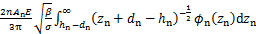(10)

其中：φ_n(z_n)是高度为标准高斯分布的概率密度函数。

2.2　泊松比

单个微凸体接触的切向应力应变关系可表示为^[10]

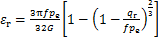(11)

式中：ε_r为切应变；q_r为剪切强度，与材料的屈服强度S_y相关，对于钢材，q_r=0.6S_y；f为摩擦因数；p_e为法向压力。则单个微凸体的剪切模量可以表示为

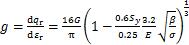(12)

其中：法向载荷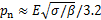^[10]。虚拟材料层的剪切模量可以表示为

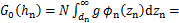
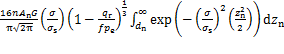(13)

虚拟材料层的泊松比可以表示为

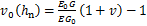(14)

2.3　密度

虚拟材料层的密度可以表示为

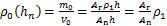(15)

式中：ρ₁为接触体的密度；A_r为粗糙界面的实际接触面积，

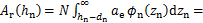
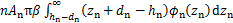(16)

则虚拟材料层的密度可以表示为

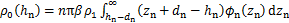(17)

2.4　厚度

对粗糙表面形貌的Greenwood-Williamson统计模型描述，微凸体的高度分布为标准高斯分布，微凸体高度分布在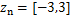的概率为99.73%^[19]。当虚拟材料层的厚度h=6σ_s时，可以覆盖粗糙界面上所有的微凸体。同时，考虑到接触体之间的距离改变时，微凸体产生变形，虚拟材料的厚度也相应改变。因此，虚拟材料的厚度与接触体之间距离变化的关系可以表示为

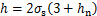(18)

式中：h_n为量纲一的粗糙面均线高度。

3 模型有效性验证

为了验证螺栓固结粗糙界面虚拟材料建模方法的准确性，进行螺栓固结结构的模态实验测试。同时，基于推导获得的虚拟材料参数，代入实验测试样品的表面粗糙形貌参数、材料参数等，建立了基于虚拟材料的螺栓固结结构有限元仿真模型，计算其固有频率与模态特性，并将有限元仿真计算结果与实验测试结果进行对比。

3.1　实验测试

设计了螺栓固结界面实验装置，进行结构模态实验测试。实验装置如图3所示。实验采用自由悬挂锤击法测试，利用力锤敲击上表面产生冲击激励，在钢板下表面安装加速度传感器，测量界面的法向加速度响应。振动分析仪型号为LMS SCADAS Mobile 8CH。

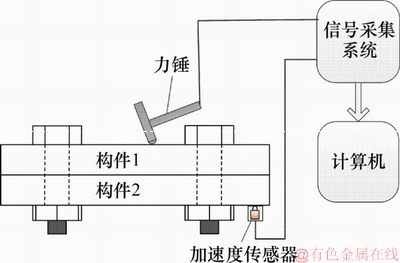
图3　实验测试示意图

Fig. 3　Schematic diagram of experimental setup

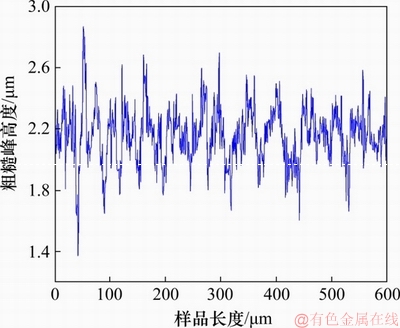
图4　实验样品表面形貌

Fig. 4　Surface topograph of test specimen

螺栓固结界面由2块长×宽×厚为300 mm×50 mm×8 mm的45号钢板，通过14个M6螺栓联接形成。名义接触面积A_n=1.5×10^-2 m²。通过扭力扳手给每个螺栓施加5 N·m的力矩，当拧紧6个螺栓时，界面的平均压力为p=1.67 MPa。采用激光共聚焦显微镜LEXT对相互接触的2块钢板表面进行表面形貌测试，采样间隔为0.625 μm。钢板表面形貌如图4所示。

表面形貌参数采用下式计算^[22]：

；

；

。

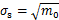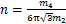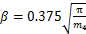式中：m₀，m₂和m₄为粗糙表面的谱矩^[22]，

，

,

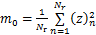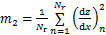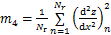
其中：N_r为粗糙表面的数据点总数。

将计算获得的表面形貌参数σ_s=1.07 μm，n=3.09×10¹¹ m^-2，β=0.315 μm以及等效弹性模量E=115.4 GPa代入式(10)，(14)和(17)，获得虚拟材料参数：E₀=255 MPa，v₀=0.375，ρ₀=7 700 kg/m³。

3.2　基于虚拟材料的有限元仿真分析

基于计算获得的螺栓固结界面虚拟材料参数，采用有限元仿真计算方法对螺栓联接界面系统进行模态分析，获得系统的固有频率与模态特性。基于虚拟材料的螺栓联接结构有限元分析模型如图5所示。钢板和虚拟材料层均采用SOLID185单元离散，虚拟材料层与上下钢板共节点连接。实验测试获得的前5阶固有频率和其中3阶模态与有限元计算获得的固有频率和模态的对比，分别如图6和表1所示。

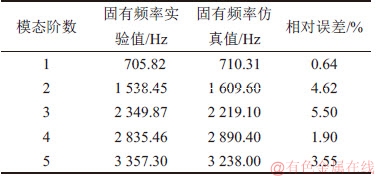
由图6和表1可知：实验测得的固有频率与基于虚拟材料模型计算值相对误差小于6%，且各阶模态一致，说明本文的虚拟材料建模方法与材料参数的计算模型是有效的。

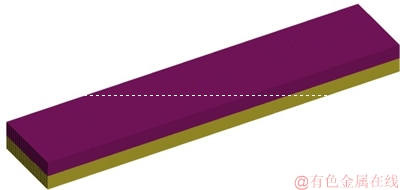
图5　基于虚拟材料的螺栓联接结构有限元分析模型

Fig. 5　Finite element analysis model for bolted jointed structure based on virtual material model

表1　固有频率实验值与仿真值对比

Table 1　Comparison between natural frequencies from experimental test and FEA

4 虚拟材料参数与接触刚度特性分析

改变界面的接触特性参数，包括粗糙表面的形貌参数和接触基体材料属性，获得不同界面特性参数时螺栓固结界面虚拟材料参数和界面的接触刚度随界面压力的变化关系曲线。3种具有不同表面粗糙度的界面分别为光滑界面、中等粗糙界面和粗糙界面，其表面形貌参数如表2所示。不同接触基体的材料参数如表3所示。对不同粗糙度和不同接触基体的界面，采用式(10)，(13)，(14)，(17)，(18)和(3)计算获得螺栓固结界面的虚拟材料参数和接触刚度随界面压力的变化关系曲线。

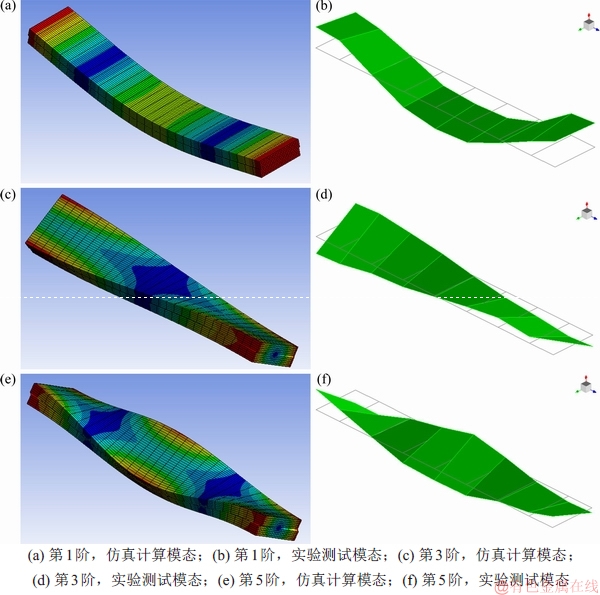
图6　不同阶数的实验测试模态与仿真计算模态对比

Fig. 6　Comparison of vibration mode shapes between simulation and experiment

表2　不同粗糙度表面形貌参数

Table 2　Parameters of surfaces with different roughness

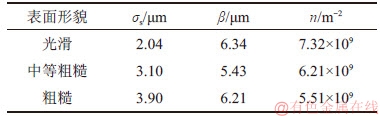
表3　不同接触基体的材料参数

Table 3　Material and sound parameters of different contact bodies

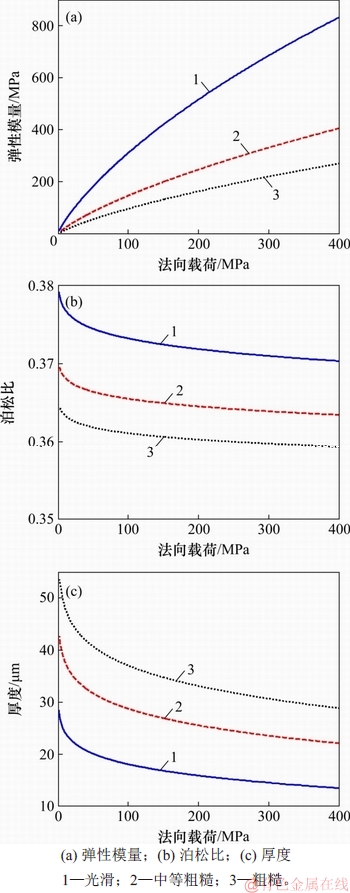
图7　不同表面粗糙度时虚拟材料的材料参数随法向载荷的变化关系

Fig. 7　Plots of virtual material parameters versus normal load for surfaces with different roughness

4.1　虚拟材料参数变化特性

当表面粗糙度不同时，虚拟材料的弹性模量、泊松比和厚度随法向载荷的变化关系曲线如图7所示。接触基体的材料属性为钢。

由图7可知：对具有不同粗糙度的表面，虚拟材料的弹性模量随着法向载荷的增大而增大，而泊松比和虚拟材料的厚度均随着法向载荷的增大而递减；在相同载荷变化范围内，虚拟材料的弹性模量和厚度随法向载荷剧烈变化，而泊松比的变化较小，即随着接触界面法向载荷变化，引起粗糙界面接触特性发生变化，在等效的虚拟材料参数中，弹性模量和厚度更显著地表征接触变化特性。

由图7还可知：在相同载荷作用下，随着界面粗糙度增大，虚拟材料的弹性模量、泊松比均减小，而虚拟材料的厚度递增。

当接触基体不同时，虚拟材料的弹性模量、泊松比和厚度随法向载荷的变化关系曲线如图8所示，界面为中等粗糙度。

由图8(a)可知：与钢基体相比，基体为铸铁和铝时，虚拟材料的弹性模量降低。这是因为钢材、铸铁和铝的弹性模量依次递减(见表3)。由图8(b)可知：当接触基体材料不同时，钢基体虚拟材料的泊松比最大，铝基体次之。这是因为铸铁的泊松比最小，其相应的虚拟材料的泊松比也最小；同时，随着基体材料的弹性模量减小，虚拟材料的厚度也递减：在相同载荷作用下，钢基体材料的虚拟材料厚度最大，铝基体材料的厚度最小。

4.2　接触刚度特性

不同表面粗糙度时界面接触刚度随法向载荷的变化关系曲线如图9所示，接触基体的材料属性为钢。

由图9可知：对具有不同粗糙度的表面，界面接触刚度均随着法向载荷的增加而递增，其中，光滑接触界面的刚度最大，粗糙界面的刚度最小，界面接触刚度随着表面粗糙度的增大而递减。

当接触基体不同时，虚界面接触刚度随法向载荷的变化关系曲线如图10所示，界面为中等粗糙度。

由图10可知：与钢基体相比，基体为铸铁和铝时，界面接触刚度依次递减，铸铁基体次之，铝基体最小；当法向载荷较小时(p<50 MPa)，接触基体材料属性的差异对界面接触刚度的影响较小；随着法向载荷增大，接触基体材料属性的影响增大。

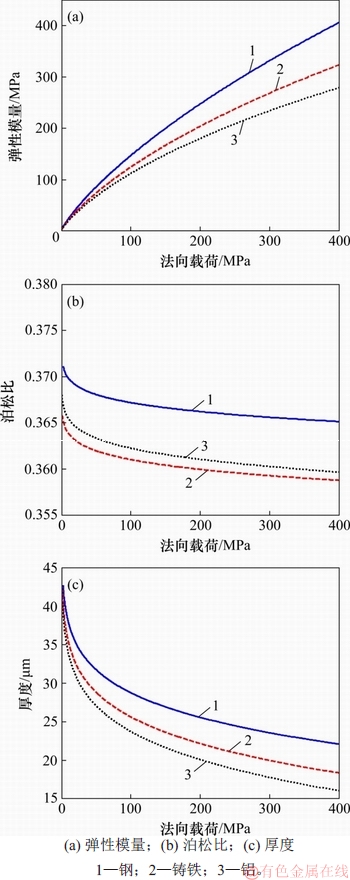
图8　不同接触基体时虚拟材料的材料参数随法向载荷的变化关系

Fig. 8　Plots of virtual material parameters versus normal load for different contacting bodies

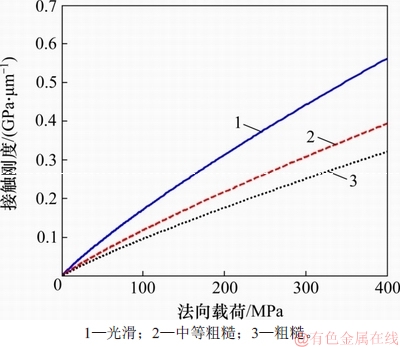
图9　不同表面粗糙度时粗糙界面接触刚度随法向载荷的变化关系

Fig. 9　Plots of contact stiffness versus normal load for surfaces with different roughness

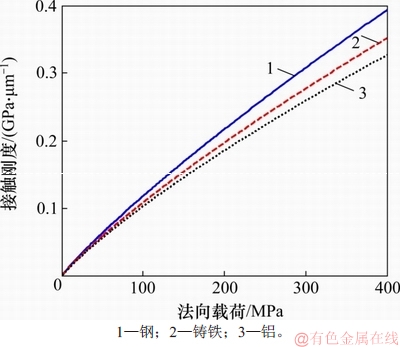
图10　不同接触基体时粗糙界面接触刚度随法向载荷的变化关系

Fig. 10　Plots of contact stiffness versus normal load for different contacting bodies

5 结论

1) 提出了一种基于统计学模型的粗糙接触界面虚拟材料建模方法，推导了虚拟材料的弹性模量、泊松比、密度和厚度等材料参数的解析表达式，分析了螺栓固结界面的表面粗糙形貌、基体材料属性对虚拟材料的材料参数和界面接触刚度的影响特性。

2) 通过螺栓联接结构的模态实验测试和基于虚拟材料的有限元仿真分析，验证了粗糙接触界面虚拟材料建模方法的正确性。

3) 虚拟材料的材料参数与法向载荷、界面粗糙度和接触基体弹性模量相关：随法向载荷和基体弹性模量的增加，虚拟材料的弹性模量增大，泊松比和厚度减少；随界面粗糙度的增加，弹性模量和泊松比减少，而厚度增大。

4) 螺栓固结界面接触刚度随法向载荷增大而递增，随界面粗糙增大而减小。

参考文献：

[1] DAOUK S, LOUF F, CLUZEL C, et al. Study of the dynamic behavior of a bolted joint under heavy loadings[J]. Journal of Sound and Vibration, 2017, 392: 307-324.

[2] HAMMAMI C, BALMES E, GUSKOV M. Numerical design and test on an assembled structure of a bolted joint with viscoelastic damping[J]. Mechanical Systems and Signal Processing, 2016, 70/71: 714-724.

[3] CHOI J I, HASHEMINIA S M, CHUN H J, et al. Failure load prediction of composite bolted joint with clamping force[J]. Composite Structures, 2018, 189: 247-255.

[4] CAO Yuejie, CAO Zengqiang, ZUO Yangjie, et al. Numerical and experimental investigation of fitting tolerance effects on damage and failure of CFRP/Ti double-lap single-bolt joints[J]. Aerospace Science and Technology, 2018, 78: 461-470.

[5] XIAO Huifang, SHAO Yimin, XU Jinwu. Investigation into the energy dissipation of a lap joint using the one-dimensional microslip friction model[J]. European Journal of Mechanics: A, 2014, 43: 1-8.

[6] ARMAND J, SALLES L, SCHWINGSHACKL C W, et al. On the effects of roughness on the nonlinear dynamics of a bolted joint: A multiscale analysis[J]. European Journal of Mechanics: A, 2018, 70: 44-57.

[7] 王雯, 吴洁蓓, 傅卫平, 等. 机械结合面法向动态接触刚度理论模型与试验研究[J]. 机械工程学报, 2016, 52(13): 123-130.

WANG Wen, WU Jiebei, FU Weiping, et al. Theoretical and experimental research on normal dynamic contact stiffness of machined joint surfaces[J]. Journal of Mechanical Engineering, 2016, 52(13): 123-130.

[8] 傅卫平, 娄雷亭, 高志强, 等. 机械结合面法向接触刚度和阻尼的理论模型[J]. 机械工程学报, 2017, 53(9): 73-82.

FU Weiping, LOU Leiting, GAO Zhiqiang, et al. Theoretical model for the contact stiffness and damping of mechanical joint surface[J]. Journal of Mechanical Engineering, 2017, 53(9): 73-82.

[9] YOSHIMUAR M. Computer-aided design improvement of machine tool structure incorporating joint dynamics data[J]. Annals of the CIRP, 1979, 28(1): 241-246.

[10] MAO Kuanmin, LI Bin, WU Jun, et al. Stiffness influential factors-based dynamic modeling and its parameter identification method of fixed joints in machine tools[J]. International Journal of Machine Tools and Manufacture, 2010, 50(2): 156-164.

[11] 田红亮, 刘芙蓉, 方子帆, 等. 引入各向同性虚拟材料的固定结合部模型[J]. 振动工程学报, 2013, 26(4): 561-573.

TIAN Hongliang, LIU Furong, FANG Zifan, et al. Immovable joint surface's model using isotropic virtual material[J]. Journal of Vibration Engineering, 2013, 26(4): 561-573.

[12] 李小彭, 梁亚敏, 郭浩, 等. 结合面广义间隙的等效模型研究[J]. 振动工程学报, 2014, 27(1): 25-32.

LI Xiaopeng, LIANG Yamin, GUO Hao, et al. Study on equivalent model of generalized clearance of joint surface[J]. Journal of Vibration Engineering, 2014, 27(1): 25-32.

[13] 孙清超, 黄庆涛, 孙志勇, 等. 基于梯度虚拟材料的栓接结合部连接参数表征[J]. 机械工程学报, 2018, 54(11): 102-109.

SUN Qingchao, HUANG Qingtao, SUN Zhiyong, et al. Interface parameter identification of bolted connections based on gradient virtual material[J]. Journal of Mechanical Engineering, 2018, 54(11): 102-109.

[14] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces[J]. ASME Journal of Tribology, 1991, 113: 1-11.

[15] MORAG Y, ETSION I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces[J]. Wear, 2007, 262(5/6): 624-629.

[16] LIOU J L, LIN J F. A modified fractal microcontact model developed for asperity heights with variable morphology parameters[J]. Wear, 2010, 268(1/2): 133-144.

[17] GONZALES-VALADEZ M, DWYER-JOYCE R S, LEWIS R. Ultrasonic reflection from mixed liquid-solid contacts and the determination of interface stiffness[J]. Tribology and Interface Engineering Series, 2005, 48: 313-320.

[18] JOHNSON K L. Contact Mechanics[M]. Cambridge: Cambridge University Press, 1985: 90-94.

[19] SOJOUDIH, KHONSARIM M. On the modeling of quasi-steady and unsteady dynamic friction in sliding lubricated line contact[J]. Journal of Tribology, 2010, 132: 012101.

[20] BUSH A W, GIBSON R D, KEOGH G P. The limit of elastic deformation in the contact of rough surfaces[J]. Mechanics Research Communications, 1976, 3(3): 169-174.

（编辑 赵俊）

收稿日期： 2018 -09 -27; 修回日期： 2018 -11 -03

基金项目(Foundation item)：国家自然科学基金资助项目(51775037) (Project(51775037) supported by the National Natural Science Foundation of China)

通信作者：肖会芳，博士，副教授，从事机械结构界面动力学研究；E-mail：huifangxiao@ustb.edu.cn