Analysis of damage localization for ductile metal

in process of shear band propagation

WANG Xue-bin(王学滨)

Department of Mechanics and Engineering Sciences, Liaoning Technical University, Fuxin 123000, China

Received 10 March 2005; accepted 19 April 2005

Abstract: Distribution of localized damage in shear band can’ t be predicted theoretically based on classical elastoplastic theory. The average damage variable in shear band was considered to be a non-local variable. Based on non-local theory, an analytical expression for the localized damage in strain-softening region of shear band in the process of shear band propagation was presented using boundary condition and symmetry of local damage variable, etc. The results show that dynamic shear softening modulus, dynamic shear strength and shear elastic modulus influence the distribution of the localized damage in shear band. Internal length of ductile metal only governs the thickness of shear band. In the strain-softening region of shear band, the local damage variable along shear band’s tangential and normal directions is non-linear and highly non-uniform. The non-uniformities in the normal and tangential directions of shear band stem from the interactions and interplaying among microstructures and the non-uniform distribution of shear stress, respectively. At the tail of the strain-softening region, the maximum value of local damage variable reaches 1. This means that material at this position fractures completely. At the tip of shear band and upper as well as lower boundaries, no damage occurs. Local damage variable increases as dynamic shear softening modulus decreases or shear elastic modulus increases, leading to difficulty in identification or detection of damage for less ductile metal material at higher strain rates.

Keywords: shear band; ductile metal; damage localization; non-local theory; strain rate; shear stress; strain-softening

1 Introduction

Shear localization is an important and often dominating deformation and failure mechanism for Ti and Ti alloy in dynamic loadings[1—10]. The eventual outcome of localized deformation is ductile rupture and material separation. Shear localization occurs and plays an important role in engineering applications.

To predict the distribution of plastic shear strain in shear band and the thickness of the band, some modifications and generalization from the standard continuum description must be carried out. One of the most promising approaches is the second order gradient continuum that incorporates the second order spatial gradients of plastic strain in the yield function. In gradient-dependent plasticity, the characteristic length describes the interactions and interplaying among microstructures. For Ti and Ti alloy the texture is heterogeneous to some extent and a certain microstructure will be influenced significantly by its neighborhoods. Interactions and interplaying among microstructures are of great importance for Ti and Ti alloy and have been studied extensively[7, 11, 12].

WANG et al[13, 14] adopted gradient-dependent plasticity to investigate shear strain localization of ductile metals, such as Ti and Ti alloy, in static[13] and dynamic loadings[14]. WANG[15] proposed a method for calculation of temperature distribution in adiabatic shear band in terms of the same theory. Beside shear strain localization of ductile metal materials, gradient-dependent plasticity has been applied into investigation of tensile strain localization for Ti and Ti alloy[16].

Some experimental observations[1—3, 10] showed that for ductile metal materials, at the initial loading stage, microcracks and induced damage appear randomly and the distributions of deformation and damage variable are relatively uniform. With the increase of strain at loading direction, damage and strain within the specimen progressively accumulate or concentrate into a certain narrow zones and localization of damage or strain occurs. The narrow zone is usually referred to shear band or localized band. Afterwards, in the process of progressive failure of material, the length of the band is increased and considerable damages and deformations are absorbed continuously by the band until ductile rupture and material separation take place. Distributions of damage and strain have hitherto been modeled numerically based on many kinds of modified and generalized elastoplastic theories[17—23]. However, analytical solution of localized damage in shear band in the process of shear band propagation has not been presented yet so far.

In the paper, the average damage variable in shear band was considered to be a non-local variable. Based on the non-local theory, an analytical expression for localized damage in strain-softening region of shear band in the process of shear band propagation was presented using boundary condition and symmetry of local damage variable, etc. Influences of related parameters on the distribution of the local damage variable were investigated through a few examples.

2 Analysis

2.1 Mechanical model for shear band propagation and basic assumptions

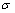A mechanical model for shear band propagation[14] is shown in Fig.1. A Ti block with a certain height and length is loaded in horizontal shear stress  and in vertical compressive stress . y-axis and x-axis are vertical and horizontal, respectively.

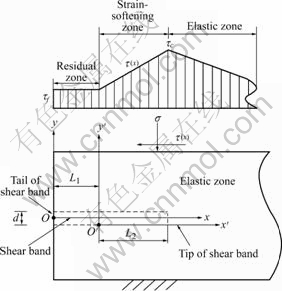
Fig.1 Shear stress acting on shear band and mechanical model for shear band propagation[14]

An important outcome of shear localization is the decrease of the stress-carrying capability of the block. Therefore, when shear stress at point O reaches the shear strength, shear localization is initiated at the point and a horizontal shear band is formed. Then, it propagates towards the right and the shear stress at point O begins to decrease. Point O is called the tail of shear band. At the tip of shear band, shear stress is maximum and attains the shear strength 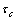. The tip moves towards the right in the process of shear band propagation. When a certain length of shear band is reached, the shear stress at point O decreases to residual shear strength τ_f . At the moment, strain-softening zone is well formed. Afterwards, residual zone appears and its length increases. Strain-softening zone moves towards the right continually. For the sake of calculation, it is assumed that the shear deformation only occurs in the horizontal direction. The total length of shear band is L₁+L₂. The thickness of shear band is d. L₁ is the length of the residual zone. L₂ is the length of strain-softening zone. In front of the tip of shear band, shear stress is lower than the shear strength and material still remains elastic.

Some experimental results show that the post-peak stress-strain curve of Ti or Ti alloy under dynamic loadings exhibits approximately linear strain-softening behavior[6, 24]. Dynamic and static post-peak constitu- tive relations are shown in Fig.2.

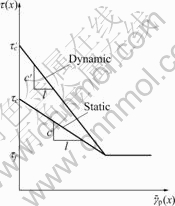
Fig.2 Dynamic and static post-peak constitutive relations[14]

2.2 Analysis of elastic, plastic and total strains in strain-softening zone of shear band

According to shear Hooke’s law, the elastic shear strain γ_e(x) in strain-softening zone can be expressed as

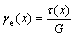                                (1)

where  G is the shear elastic modulus; τ(x) is the shear stress, and x∈[L₁, L₁+L₂].

According to WANG et al[13, 14], the plastic shear strain γ_p(x, y) is non-uniform in the normal direction of shear band and it is written as

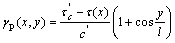                  (2)

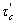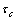where  y∈[－d/2; d/2];  and  are the dynamic and static shear strengths, respectively, 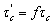;  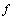is a coefficient considering strain rate effect and 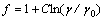, where  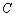is a material constant,  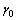and  are the strain rates in static and dynamic loading conditions, respectively; c′ and  are the dynamic and static shear softening moduli, respectively, and c′=fc; and l is the internal length parameter of ductile metal material describing the extent of heterogeneity. According to gradient-dependent plasticity[13, 14], the relation between 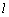 and the thickness of shear band is .

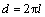If Eqn.(2) is integrated with respect to the coordinate y and then divided by d, then the average plastic shear strain 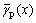 in shear band can be obtained:

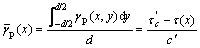              (3)

The total shear strain 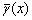 in shear band is the sum of elastic  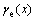and plastic  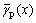parts, namely

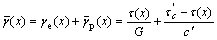           (4)

2.3 Average damage variable in shear band

According to classical damage mechanics, the relation among the shear stress, the total shear strain γ, the shear elastic modulus G and the damage variable D is

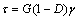                               (5)

Herein, to establish the expression for the average damage variable 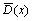 in shear band, we generalized and modified Eqn.(5) as

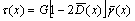                       (6)

The differences between Eqn.(6) and Eqn.(5) are obvious: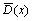 is concerned with coordinate x; the coefficient in front of  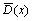is 2, not 1. Advantages of the present special definition will be discussed below.

Using Eqn.(6), 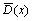 is expressed as

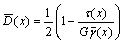                         (7)

Substitution of Eqn.(4) into Eqn.(7) leads to

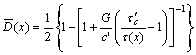             (8)

2.4 Non-local theory and local damage variable in shear band

Herein, the average damage variable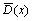 is considered to be a non-local variable. On the basis of the non-local elasticity model[25], the relation among the non-local damage variable 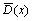, the local damage variable  and its second spatial derivative 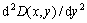 can be derived as follows:

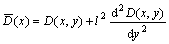                  (9)

It is noted that the derivation of Eqn.(9) is similar to that of the local plastic shear strain γ_p(y) in Ref. [13].

The following equation can be obtained by using Eqn.(9)

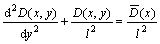                  (10)

Obviously, this is a second order homogeneous ordinary differential equation. As mentioned above, the thickness of shear band is determined by the internal length parameter, i.e., d=2πl. Consequently, the fol- lowing two conditions are needed to solve the differential equation above:

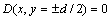                          (11)

                           (12)

In fact, Eqn.(11) is a boundary condition. It requires that no any damage occur at upper and lower boundaries of shear band. Eqn.(12) requires that the local damage variable is symmetrical with respect to the coordinate y and it is a even function due to the assumption of isotropic metal materials.

The solution of Eqn.(10) can be obtained using Eqn.(11) and Eqn.(12):

                     (13)

Substitution of Eqn.(8) into Eqn.(13) results in the following expression:

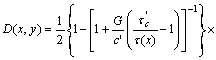
                          (14)

See Fig.1, if we use the following coordinate transformation

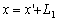                                 (15)

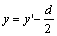                                 (16)

where  x′∈[0, L₂] and y′∈[0, d], then Eqn.(14) can be written as

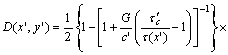
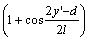                     (17)

See Fig.1, τ(x′) in the coordinate system of     x′O′y′can be expressed as

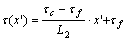                       (18)

3 Examples

The thicknesses of Ti and Ti-6Al-4V are about 10－55 μm[1, 24]. Herein, we let d=35 μm. We can obtain the internal length parameter describing the heterogeneity is about l=5.57 μm using d=2πl. Experi- mental measurements show that the shear elastic moduli for Ti and many kinds of Ti alloy are about 45 GPa. Accordingly, we let G=45 GPa. Static shear strength of Ti (τ_c=σ_c/2, where σ_c is the yield stress in uniaxial tension) is about 280 MPa. Herein, we letτ_c=280 MPa.

The length L₂ of strain-softening zone is assumed to be 20 times the thickness of shear band. For simplicity, we let τ_f =0.

Due to the non-uniform deformation of specimen beyond the onset of shear band or strain localization, the measured stress-strain curve is not a purely mechanical property or constitutive relation. The measured stress-strain curve also includes the contribution of geometrical size of specimen unless the size of the specimen is small enough. Consequently, usually, dynamic and static shear softening moduli cannot be determined through experimental tests. The pheno- menon is similar to “size effect” in rock and soil mechanics. As a result, firstly, the influence of static softening modulus c is studied and the distributions of the local damage variable for different static softening moduli are shown in Figs.3 and 4 with f =1, respec- tively.

Secondly, the influence of strain rate on the distribution of the local damage variable is shown in Fig.5 with  f=2.5 and 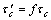=700 MPa. Finally, the influence of shear elastic modulus on the distribution of the local damage variable is shown in Fig.6 with f=1 and G=80 GPa.

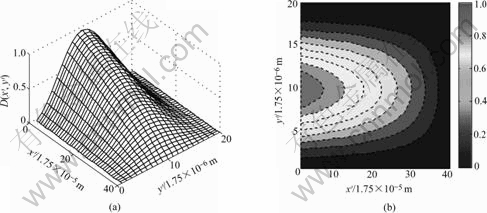
Fig.3 Three-dimensional curved surface and contour map with c=30 GPa

Fig.4 Three-dimensional curved surface and contour map with c=3 GPa

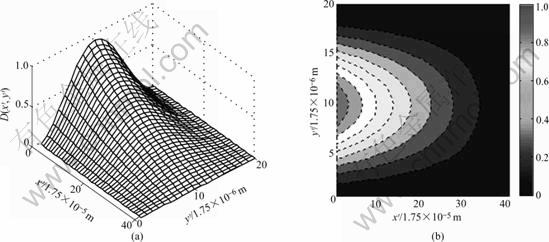
Fig.5 Three-dimensional curved surface and contour map with f=2.5

Fig.6 Three-dimensional curved surface and contour map with G=80 GPa

At the tip of shear band (x′=7×10^－4 m) and at two boundaries (y′=0 and y′=3.5×10^－5 m), the local damage variable is always zero and no any damage exists. At the tail of shear band (x′=0), the maximum local damage variable is 1, which suggests that metal material at this site has fractured completely, as is in agreement with our common knowledge, reflecting the advantage of the special expression Eqn.(6). If the coefficient in front of 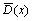 in Eqn.(6) is 1, then the maximum value of the calculated local damage variable will be 2, not 1, as is difficult to understand and not consistent with usual viewpoints.

In shear band, the local damage variable in x′and y′directions is highly non-uniform. In y′direction, the reason for the non-uniformity is due to the interactions and interplaying among microstructures. However, in x′direction, the non-uniformity is caused by the non-uniform distribution of shear stress τ(x′). In the strain-softening zone of shear band, it is assumed that τ(x′) is linear distribution in calculation. However, the obtained distribution of the local damage variable exhibits non-linear characteristic. Qualitatively, the present analytical prediction for the local damage variable in localized band is consistent with the related numerical results[17－23].

Three-dimensional curved surface near the tip of shear band becomes more steep as dynamic shear softening modulus decreases or shear elastic modulus increases, while it exhibits less steep at the tail of shear band, see Figs.3(a), 4(a), 5(a), 6(a). That is to say, the local damage variable in shear band is increased. Area with higher local damage variable is enlarged in two-dimensional contour maps as the local damage variable increases, as can be seen from Figs.3(b), 4(b), 5(b), 6(b).

The result that increasing dynamic softening modulus leads to a decrease of the local damage variable in shear band means that less ductile metal material at higher loading rates possesses a lower local damage variable, which brings a certain difficulty in identification or detection of damage.

4 Conclusions

 1) The average damage variable in shear band is considered to be a non-local variable. Based on the non-local theory, an analytical expression for the localized damage in strain-softening region of shear band in the process of shear band propagation is presented using boundary condition and symmetry of local damage variable, etc.

2) The resulting theoretical expression for localized damage in shear band shows that dynamic shear softening modulus, dynamic shear strength and shear elastic modulus influence the distribution of the localized damage in shear band. However, internal length parameter of ductile metal only governs the thickness of shear band.

3) In the strain-softening region of shear band, the local damage variable along shear band’s tangential and normal directions is non-linear and highly non-uniform. Non-uniformities of the local damage variable in the normal and tangential directions of shear band stem from the interactions or interplaying among microstructures and the non-uniform distribution of shear stress acting on the band, respectively.

4) At the tail of the strain-softening region, the maximum value of the local damage variable reaches 1. This means that material at this position fails completely. At the tip of shear band and upper as well as lower boundaries, the local damage variable is always zero and no any damage occurs.

5) Except for the tip and the tail of shear band and its two boundaries, the local damage variable within shear band is increased as dynamic shear softening modulus decrease or shear elastic modulus increases, leading to difficulty in identification or detection of damage for less ductile metal material at higher strain rates.

References

[1] Nesterenko V F, Meyers M A, Wright T W. Self-organization in the initiation of adiabatic shear bands[J]. Acta Mater, 1998, 46(1): 327－340.

[2] XU Y B, ZHONG W L, CHEN Y J. Shear localization and recrystallization in dynamic deformation of 8089 Al-Li alloy[J]. Materials Science and Engineering A, 2001, 299(1－2): 287－295.

[3] XUE Q, MEYERS M A, Nesterenko V F. Self-organization of shear bands in titanium and Ti-6Al-4V alloy[J]. Acta Materialia, 2002, 50(3): 575－596.

[4] YU Jin-qiang, ZHOU Hui-hua, SHEN Le-tian. Thermo-plastic shear bands induced during dynamic loading in Ti-55 alloys[J]. Acta Metallurgica Sinica, 1999, 35(4): 379－383. (in Chinese)

[5] LIU Wen-sheng, HUANG Bai-yun, HE Yue-hui. The room-temperature fracture mechanics of a fully-lamellar TiAl alloy[J]. J Cent South Univ Technol, 1997, 28(2): 152－155.(in Chinese)

[6] LI Qiang, XU Yong-bo, SHEN Le-tian. Dynamic mechanical properties and damage characteristics of titanium alloy (Ti-17)[J]. Acta Metallurgica Sinica, 1999, 35(5): 491－494. (in Chinese)

[7] YANG Yang, XIONG Jun, YANG Xu-yue. Microstructure evolution mechanism in adiabatic shear band in TA2[J]. Trans Nonferrous Met Soc China, 2004, 14(4): 670－674.

[8] YANG Yang, WANG Zhao-ming, ZHANG Shao-rui. Some metallurgical behaviours of adiabatic shear band on Ti side in the Ti/mild steel explosive cladding interface[J]. Rare Metal and Materials and Engineering, 1997, 26(4): 13－17. (in Chinese)

[9] Tamizifar M, Omidvar H, Mohammad Taghi Salehi S. Effect of processing parameters on shear bands in non-isothermal hot forging of Ti-6Al-4V[J]. Materials Science and Technology, 2002, 18(1): 21－29.

[10] BAI Y, BODD B. Adiabatic Shear Localization[M]. Oxford, UK: Pergamon Press, 1992.

[11] WANG Jian-hua, YI Dan-qing, WANG Bin. Microstructure and properties of 2618-Ti heat resistant aluminum alloy[J]. Trans Nonferrous Met Soc China, 2003, 13(3): 590－594.

[12] SHANG Jun-ling, LI Bang-sheng, GUO Jing-jie. Microstructure evolution during preparation of in-situ TiB reinforced titaniummatrix composites[J]. Trans Nonferrous Met Soc China, 2003, 13(2): 315－319.

[13] WANG Xue-bin, DAI Shu-hong, HAI Long. Analysis of localized shear deformation of ductile metal based on gradient-dependent plasticity[J]. Trans Nonferrous Met Soc China, 2003, 13(6): 1348－1353.

[14] WANG Xue-bin, YANG Mei, YU Hai-jun. Localized shear deformation during shear band propagation in Titanium considering interactions among microstructures[J]. Trans Nonferrous Met Soc China, 2004, 14(2): 335—339.

[15] WANG Xue-bin. Calculation of temperature distribution in adiabatic shear band based on gradient-dependent plasticity[J]. Trans Nonferrous Met Soc China, 2004, 14(6): 1062－1067.

[16] WANG Xue-bin, YANG Mei, ZHAO Yang-feng. Analytical solution for true stress-true strain curve for titanium and Ti-6Al-4V in uniaxial tension considering interactions among microstructures[J]. Rare Metal Materials and Engineering, 2005, 34(3): 346－349.

[17] DE BORST R, PAMIN J, GEERS M G D. On coupled gradient-dependent plasticity and damage theories with a view to localization analysis[J]. Eur J Mech A/Solid, 1999, 18(6): 939－962.

[18] COMI C. Computational modeling of gradient-enhanced damage in quasi-brittle materials[J]. Mechanics of Cohesive-Frictional Materials, 1999, 4(1): 17－36.

[19] Pijaudier-Cabot G, Haidar K, Dube J F. Non-local damage model with evolving internal length[J]. Int J Num Anal Methods Geomech, 2004, 28(7－8): 633－652.

[20] TANG C Y, FAN J P, LEE T C. Simulation of necking using a damage coupled finite element method [J]. Journal of Materials Processing Technology, 2003, 139(1－3): 510－513.

[21] LI C, Ellyin F. Mesomechanical approach to inhomogeneous particulate composite undergoing localized damage(Part II)－theory and application[J]. International Journal of Solids and Structures, 2000, 37(10): 1389－1401.

[22] CHUNG S W, CHOI Y J, KIM S J. Computational simulation of localized damage by finite element remeshing based on bubble packing method[J]. Computer Modeling in Engineering and Sciences, 2003, 4(6): 707－718.

[23] Patzak B, Jirasek M. Adaptive resolution of localized damage in quasi-brittle materials[J]. Journal of Engineering Mechanics, ASCE, 2004, 130(6): 720－732.

[24] LIAO S C, DUFFY J. Adiabatic shear bands in a Ti-6Al-4V Titanium alloy[J]. J Mech Phys Solids, 1998, 46(11): 2201－2231.

[25] Eringen A C, Edenlen D G B. On nonlocal elasticity[J]. Int J Engrg Science, 1972, 10(3): 233－248.

Foundation item: Project(2004F052) supported by the Educational Department of Liaoning Province, China

Corresponding author: WANG Xue-bin; Tel: +86-418-3351351; E-mail: wxbbb@263.net

(Edited by LI Xiang-qun)