Melting throughout time and energy consumption for TiAl alloys during ISM process
SU Yan-qing(苏彦庆), LIU Gui-zhong(刘贵仲), PENG Jun-jie(彭俊杰),
GUO Jing-jie(郭景杰), JIA Jun(贾 均), FU Heng-zhi(傅恒志)
(School of Materials Science and Engineering, Harbin Institute of Technology,
Harbin 150001, China)
Abstract: Based on the program developed to simulate the temperature field for ISM(Induction Skull Melting) process, the effects of power increasing rate and charge mass on the melting throughout time and the energy consumption for TiAl alloys were studied. The results show that the melting throughout time decreases exponentially with the increasing of the power increasing rate and it linearly increases with the increasing of the charge mass. There is a critical power increasing rate for different charge masses. At this critical power increasing rate, the charge can be molten when the melting power just reaches 300kW. There exists an optimal power increasing rate, i.e. 1.3kW/s. At the optimal power increasing rate, the energy consumption for melting the charge is the minimum. The charge mass has noticeable influence on the energy consumed by unit mass and the ratio of effective energy.
Key words: TiAl alloys; ISM process; melting throughout time; energy consumption CLC number: TG248
Document code: A
1 INTRODUCTION
Gamma TiAl based alloys are preferred candidates for structural materials with high specific mechanical properties used at temperature up to 900℃[1-3]. Like titanium alloys, the melt of gamma TiAl alloys is apt to be polluted by crucible materials and the atmosphere of the melting chamber. Generally, all melting methods, which adapt to melt titanium alloys, can be extended to melt gamma TiAl alloys. But gamma TiAl contains more volatile element, i.e. Al. This characteristic requests that the melting method must be convenient to control the component evaporation of TiAl melt. From this point, electron beam melting furnace, popular to melt titanium alloys industrially is not fit for melting TiAl because the evaporation loss is evident[4-7]. Up to now, induction skull melting(ISM) technique is one of the best methods to melt TiAl alloys. This technique has been used in many countries[8-11]. It combines the merits of vacuum, cold wall crucible, and induction heating. It has advantage to protect any pollution from the crucible materials and the furnace atmosphere. Induction stirring is effective for homogenizing the alloying elements in the melt. ISM can get a melt with negligible deviation to nominal composition and lower interstitial content. But that is directly related to the melt temperature, which has important influence on the activity and the evaporation rate of the components of TiAl melt[4, 12, 13]. Additionally, melt temperature has important influence on the solidification shrinkage that is very critical for minimizing the pore in the microstructure of ingot or castings[14]. For ISM process, detecting the melt temperature with thermocouples is out of valid. Many researchers have reported their investigation results about ISM[15-19], which indicated that there are quantitative relationship between the melt temperature and the melting parameters[17]. However, many other problems remain unclear, for example, the melting throughout time and the energy consumption for a given melt process. Melting throughout time refers to the time when all the charge are molten down except the skull. If the melting time is shorter than the melting throughout time, there will remain some raw materials of the charge and as a result the composition will deviate from the nominal composition remarkably. Energy consumption for a melt can change in a wide range. But the effect of melting parameter on the energy consumption is a virgin field up to now. In this paper, the melting throughout time and the energy consumption were studied with the aid of a temperature field simulation program[17].
2 INFLUENCE OF CHARGE MASS AND POWER INCREASING RATE ON MELTING THROUGH- OUT TIME
The melting throughout time when different melting power increasing rates(q) of 0.75, 1, 1.5, 3 and 6kW/s was exerted on different charge masses of 3.0, 3.5, 4.0, 4.5 and 5.0kg was recorded. The applied melting power increases to 300kW at different increasing rates and then no change is observed, as shown in Fig.1. This manner is analogous to the melting practice.
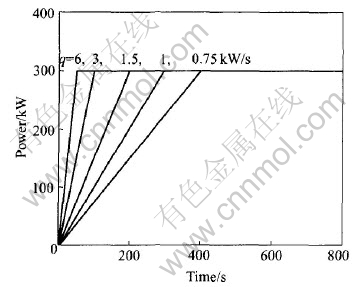
Fig.1 Power increasing mode applied in calculation
The calculation results are listed in Table 1. Based on Table 1, the influence of melting power increasing rate on the melting throughout time are plotted in Fig.2 as the scattered points. The smooth lines are the regression results. From Fig.2, the melting throughout time decreases exponentially with the increasing of the melting power increasing rate for different charge masses. This relationship can be expressed as Eqn.(1) and the parameters are listed in Table 2.
t=t0+A1exp(-q/t1)+A2exp(-q/t2)(1)
The effect of charge mass on the melting throughout time was plotted in Fig.3. It can be seen that there is a linear relationship as shown in
Table 1 Melting-throughout time under different conditions (s)

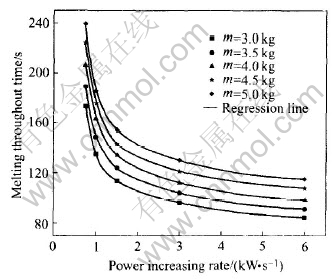
Fig.2 Melting throughout time vs power increasing rate
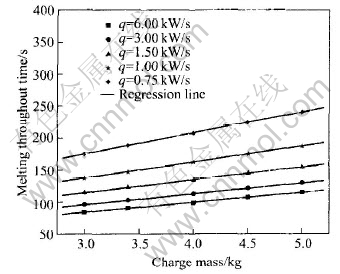
Fig.3 Melting throughout time vs charge mass
Table 2 Parameters in Eqn.(1)

Eqn.(2) and the parameters are listed in Table 3.
t=B1+B2·m(2)
Table 3 Parameters in Eqn.(2)
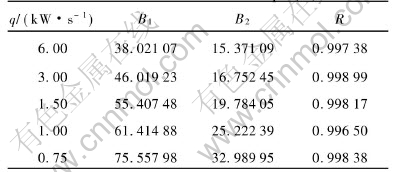
The above results show that the melting throughout time is determined by two factors, i.e. the charge mass and the power increasing rate. In Eqns.(1) or (2), the melting throughout time is controlled by one factor and the parameters are controlled by the other factor. For example, Eqn.(2) expresses the effect of the charge mass on the melting throughout time. The parameters A2 and B2 in Eqn.(2) are controlled by the power increasing rate and vice versa. In other words, there is a combined effects of the charge mass and the power increasing rate on the melting throughout time. Now we can set up the relationship between the parameters in Eqn.(2) and the power increasing rate. As shown in Fig.4, the scattered points are the parameter values of B1 and B2 at different power increasing rates, and the smooth lines are the regression results. Eqns.(3) and (4) for describing regression lines in Fig.4 are also the exponent function, which is similar to Eqn.(1).
B1=34.03223+3755.34455×exp(-q/0.13338)+36.91545×exp(-q/2.68788)(3)
R2=0.99991
B2=15.01018+159.76539×exp(-q/0.29245)+8.43942×exp(-q/1.8935)(4)
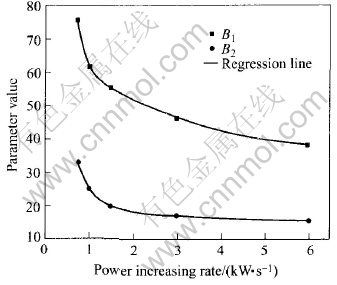
Fig.4 Parameters in Eqn.(2) vs power increasing rate

Fig.5 Critical q for different charge masses
From Eqns.(2), (3) and (4), the melting throughout time increases linearly with the increasing of the charge mass and decreases exponentially with the increasing of the power increasing rate.
3 INFLUENCE OF CHARGE MASS AND MELTING POWER INCREASING RATE ON ENERGY CONSUMPTION
If we integrate melting power with the melting time, the energy consumed under different conditions can be known. From Fig.5, it can be seen that the effect of the charge mass and the melting power increasing rate on the melting throughout time is complex. With the variation of the charge mass, the melting power increasing route is different. For example, when the charge mass is 5.0kg, the melting power increasing rate is large than 3kW/s, and not all the charge are molten when the melting power reaches 300kW. The melting power must be held at 300kW for an extra period to ensure the charge is molten throughout. If the melting power increasing rate is less than 1.5kW/s, before the melting power reaches 300kW, the charge has been all molten down. So the integrating routes have two cases: 1) if the charge is molten down before the melting power reaches 300kW, then the energy consumption is calculated with Eqn.(5); 2) if the melting power reaches 300kW at t moment and the charge is not molten down, and it needs to hold the power to t′ moment, then the energy is calculated with Eqn.(6).
E=P·t/2=q·t2/2(5)
E=P·t2/2+300(t′-t)(6)
Fig.6 illustrates the effect of the charge mass on the energy consumption for different power increasing rates. From Eqns.(2), (5) and (6), the energy consumption increases with the increasing of the charge mass according to a two times function. Regressing result for the scattered points in Fig.6 is shown in Eqn.(7) and the parameters in the equation are listed in Table 4.
E=A3+B3·m+C3·m2(7)
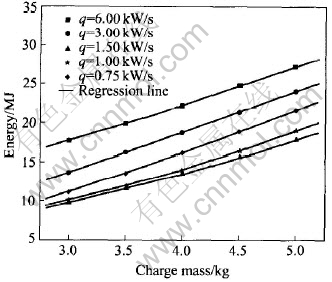
Fig.6 Energy vs charge mass
Table 4 Parameters in Eqn.(7)

In Fig.5, for different charge masses, there is a critical power increasing rate. At this rate, all the charge are molten down when the power just reaches 300kW. This critical power increasing rate is denoted with special symbols(□) in Fig.5. The quantitative relationship between the critical power increasing rate and the charge mass is plotted in Fig.7 and the regressed function is listed in Eqn.(8).
qc=5.86859-1.1331·m+0.07781·m2(8)
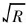 =0.99996
=0.99996
For a given charge mass, the influence of the power increasing rate on the energy consumption is illustrated in Fig.8 and the line across the other five lines is the critical power increasing rate for different charge masses. It can be found that, on the both sides of the critical power increasing rate, the energy consumption varies according to distinctive different rules. On the right of the critical line, the energy will increase with the increasing of the power increasing rate monotonously. But on the left, there is the optimum power increasing rate. At this value, the energy consumed by differ-ent charge masses is the minimum. For the left
Fig.7 Critical q for different charge masses
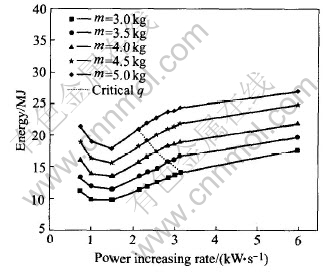
Fig.8 Energy vs power increasing rate
part of the critical line, the regression relationship between the consumption energy and the power increasing rate is written as Eqn.(9) and the parameters for different charge masses are listed in Table 5.
E=A4+B4·q+C4·q2+D4·q3(9)
From Eqn.(9) and Table 5, the optimal power increasing rate for 3.0 to 5.0kg charge is (1.3±0.05)kW/s. At this increasing rate, the melting throughout time and the energy consumption for different charge masses are plotted in Fig.9 and the regression functions are written as Eqns.(10) and (11).
tm=58.628+20.42m(10)
R=0.99875
Emin=3385.51502+944.09882m+384.58168m2(11)
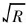 =0.99981
=0.99981
Based on the above results, other information for preserving energy can be concluded. One is the energy consumed by unit charge mass(Emin/m). As shown in Fig.10, when the charge mass is 3.0kg, Emin/m is the minimum. The other is the ratio of
Table 5 Parameters in Eqn.(9)

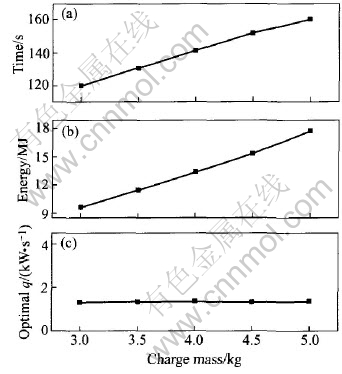
Fig.9 Influence of charge mass on energy consumption and melting throughout time under optimal power increasing rate
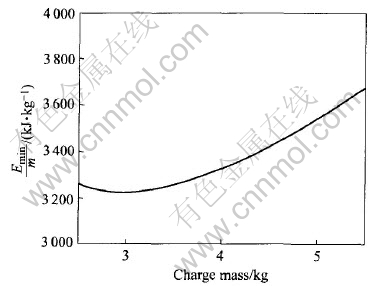
Fig.10 Influence of charge mass on energy consumption by unit mass
the necessary energy for heating up different charge mass to melting point to the total energy consumption (Q/Emin). Q can be calculated by Eqns.(12) and (13).
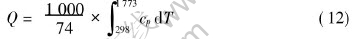
cp=55.940+5.94×10-3T-7.531×105T-2(13)
And then Q=1210.8kJ/kg. Since
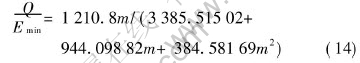
The varying curve of Q/Emin as shown in Fig.11 indicates that when the charge mass is 3kg, the ratio of the useful energy is the maximum, i.e. 0.3753.

Fig.11 Influence of charge mass on ratio of useful energy
4 CONCLUSIONS
For ISM processing, the melting power increasing rate and the charge mass have very important effect on the melting throughout time and the energy consumption.
1) The melting throughout time decreases exponentially with the increasing of the power increasing rate and it linearly increases with the increasing of the charge mass.
2) There is a critical power increasing rate for different charge masses to melt down the charge when the melting power just arrives 300kW. The quantitative relationship between the critical rate and the charge mass is qc=5.86859-1.1331m+0.07781m2.
3) The energy consumption for melting down all the charge at different charge masses abides a function as follows: E=A3+B3·m+C3·m2.
4) The influence of the melting power increasing rate on the energy consumption is complex. When the rate is less than the critical rate, there is an optimal rate, at which the energy consumption is the minimum and the rate is 1.3kW/s.
5) At the optimal power increasing rate, the charge mass has noticeable influence on the energy consumed by unit mass and the ratio of effective energy. When the charge mass is 3kg, the two concerned parameters all get the optimal values.
REFERENCES
[1]Dimiduk D M. Gamma titanium aluminide alloys—An assessment within the competition of aerospace structural materials [J]. Materials Science and Engineering, 1999, A263: 281-288.
[2]Loria E A. Gamma titanium aluminides as prospective structural materials [J]. Intermetallics, 2000, 8: 1339-1345.
[3]Loria E A. Quo-vadis gamma titanium aluminide [J]. Intermetallics, 2001, 9: 997-1001.
[4]Maeda M, Kiwake T, Shibuya K, et al. Activity of aluminum in molten Ti-Al alloys [J]. Materials Science and Engineering, 1997, A239-240: 276-280.
[5]Powell A, Avyle V D, Damkroger B. Analysis of multi-component evaporation in electron beam melting and refining of titanium alloys [J]. Metallurgical and Materials B, 1997, 28B(6): 1227-1234.
[6]Ogasawara Y, Hadi T, Seyed M. Rates of evaporation in a vacuum in liquid Ni-Ti alloys [J]. ISIJ International, 1998, 38(8): 789-793.
[7]Isawa T, Nakamura H, Murakami K. Aluminum evaporation from titanium alloys in EB hearth melting process [J]. ISIJ International, 1992, 32(5): 607-615.
[8]Roberts R J. Larger-scale cold crucible melting of titanium and its alloys [J]. Transactions of the American Foundrymens Society, 1996, 104: 523-528.
[9]GUO Jing-jie, SU Yan-qing, JIA Jun, et al. Mechanism of skull formation during induction skull melting of intermetallic compounds [J]. International Journal of Cast Metals Research, 1999, 12(1): 35-40.
[10]Baake E, Nacke B, Bernier F, et al. Experimental and numerical investigations of the temperature field and melt flow in the induction furnace with cold crucible [J]. COMPEL - The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 2003, 22(1), 88-97.
[11]Tetsui T, Ono S. Endurance and composition and microstructure effects on endurance of TiAl used in turbochargers [J]. Intermetallics, 1999, 7: 689-697.
[12]Guo J J, Liu Y, Su Y Q, et al. Evaporation behavior of aluminum during the cold crucible induction skull melting of titanium aluminum alloys [J]. Metallurgical and Materials Transactions B, 2000, 31B(4): P837-844.
[13]Su Y Q, Guo J J, Jia J, et al. Composition control of a TiAl melt during the induction skull melting (ISM) process [J]. Journal of Alloys and Compounds, 2002, 334: 261-266.
[14]SU Yan-qing, LIU Chang, BI Wei-sheng, et al. Influence of casting processes on shrinkage distribution in TiAl based alloy shaft castings [J]. Special Casting & Nonferrous Alloys, 2002(5): 11-15 .
[15]Negrini F, Fabbri M, Zuccarini M, et al. Electromagnetic control of the meniscus shape during casting in a high frequency magnetic field [J]. Energy Conversion & Management, 2000, 41: 1687-1701.
[16]Bojarevics V V, Pelricleous K. Modeling the dynamics of magnetic semilevitation melting [J]. Metallurgical and Materials Transactions B, 2000, 31B(1): 179-189.
[17]SU Yan-qing, GUO Jing-jie, LIU Gui-zhong, et al. Temperature control of TiAl melt during induction skull melting (ISM) process [J]. Materials Science and Technology, 2001, 17(11): 1434-1440.
[18]Morita A, Fukui H, Tadano H, et al. Alloying titanium and tantalum by cold crucible levitation melting (CCLM) furnace [J]. Materials Science and Engineering, 2000, 280A: 208-213.
[19]Morisue T, Yajima T, Kume T, et al. Analysis of electromagnetic force for shaping the free surface of a molten melt in a cold crucible [J]. IEEE Transactions on Magnetic, 1993, 29(2): 1562-1565.
(Edited by YANG Bing)
Foundation item: Project(50271020; 50395102) supported by the National Natural Science Foundation of China; Project(2002AA305209) supported by Hi-tech Research and Development Program of China
Received date: 2004-06-15; Accepted date: 2004-11-16
Correspondence: SU Yan-qing, Professor, PhD; Tel: +86-451-86418415; Fax: +86-451-86415776; E-mail: suyq@hit.edu.cn