DOI: 10.11817/j.issn.1672-7207.2019.01.005
Ti6Al4V合金粉末高温高压成形过程中粉固界面及其耦合变形研究
季晨昊，郎利辉，黄西娜，孟凡迪，徐文才
(北京航空航天大学 机械工程及自动化学院，北京，100083)
摘要：通过数值模拟和热等静压(HIP)试验，研究Ti6Al4V合金粉末热等静压成形过程中与包套的接触状态，建立热等静压力学模型以及摩擦因数的力学方程，基于数值模拟结果，根据粉末致密化理论就接触模型对摩擦因数、相对密度、相对位移的影响进行分析和讨论。研究结果表明：在热等静压过程中，Shima模型对描述Ti6Al4V合金粉末的致密化过程具有较高精度，圆柱试验件尺寸数值模拟结果与试验结果的相对误差在5%以内；Stick-slip模型对于摩擦因数的变化过程以及相对位移的变化趋势的预测结果与实际一致，摩擦因数稳定值为0.15；Bilinear模型对于相对密度变化趋势的预测结果与实际一致，相对密度误差为1%；采用Stick-slip模型可以准确地预测包套的变形及粉末的致密化过程。
关键词：Ti6Al4V合金；热等静压；数值模拟；接触模型
中图分类号：TF124 文献标志码：A 文章编号：1672-7207(2019)01-0029-09
Research on powder-solid interface and coupling deformation of Ti6Al4V alloy powder during high temperature and high pressure
JI Chenhao, LANG Lihui, HUANG Xina, MENG Fandi, XU Wencai
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100083, China)
Abstract: In order to study the contact state of Ti6Al4V alloy during hot isostatic pressing(HIP), numerical simulations and HIP test were carried out. The mechanical model and mechanical equation considering friction coefficient of HIP was proposed. According to the theory of powder densification, the impact of the contact model on friction coefficient, relative density and relative displacement was discussed based on numerical simulation results. The results show that the Shima model describes the densification process of Ti6Al4V alloy powder with high precision. The cylindrical capsule size error between numerical simulation and experiment is less than 5%. The predicted results of Stick-slip model in the variation trend of coefficient friction and relative displacement are consistent with the actual situation. The predicted results of Bilinear model in the changing trend of relative density are consistent with the actual situation. The coefficient of friction is stable at 0.15. The error of relative density between numerical simulation and experiment is only 1%. The Stick-slip model can accurately predict the deformation of the capsule and the densification process of the powder.
Key words: Ti6Al4V alloy; hot isostatic pressing; numerical simulation; contact model
钛合金具有较高的比强度，同时钛合金的耐热性、耐蚀性、抗弹性良好[1]，广泛应用于航空航天、军事和船舶等领域。传统加工方式对钛合金的加工存在一些问题，如铸造会产生缩孔、缩松，锻造后续机加工周期长等。热等静压作为粉末近净成形的一种有效方法，克服了钛合金传统成形工艺上的不足[2]。热等静压技术是一种在高温、高压条件下通过包套对粉末材料进行直接固结成形的技术。热等静压产品致密度高、力学性能优越，极大提高了材料的利用率，成为钛合金、铝合金等零件成形的最有效方法之一[3]。热等静压过程中，粉末颗粒在压力与温度的共同作用下转变为高度致密化体，正是由于这种转变，粉固界面的接触状态在热等静压过程中的每一步都是不明确的，而且粉末与包套之间的摩擦阻碍了最优致密度的形成。摩擦对于粉末成形过程的理解和分析具有重要的作用。相关研究报告显示，许多粉末制件的最终性能强烈依赖于粉末与壁面的摩擦[4]，而且热等静压件的一些缺陷例如裂纹、包套破裂等的产生与粉固界面的接触状态密切相关。粉末热等静压成形过程是一个高度复杂的非线性化过程[5]，难以通过数值解析方法控形，而采用反复试验的方法不仅费时，而且极大地增加了成本。数值模拟成为研究粉末热等静压成形过程的一种快速、有效的手段。而在数值模拟过程中，粉固界面的接触处理是关键一步，粉固界面接触对严重影响着数值模拟结果，不当的处理严重降低数值模拟的可靠性，失去其指导意义。目前，针对热等静压过程中粉固界面的研究鲜有报道，热等静压过程中包套与粉末的接触受到多方面的影响，这种接触的具体模型也很难从实验中直接得出，王刚[6]认为热等静压过程中2A12合金粉末与包套之间没有相对位移，不必考虑包套与粉末的摩擦；刘国承等[7]采用库仑摩擦模型模拟316L粉末与包套的接触，并得到了近似尺寸；瞿宗宏等[8]采用粘滑摩擦模型处理FGH4097合金粉末与包套之间的接触并得到了准确的成形尺寸及变形趋势，而关于Ti6Al4V合金粉固界面的研究，还没有相关报道。因此，有必要展开对Ti6Al4V粉末与包套之间接触以及摩擦力的研究。本文作者针对Ti6Al4V合金成形开展数值模拟研究工作，建立热等静压力学模型，分析粉固界面的接触状态，研究粉固界面接触状态对热等静压成形过程的影响，对Ti6Al4V合金热等静压包套设计及工艺参数优化具有重要意义。
1 接触模型及材料本构方程
1.1 接触模型
1.1.1 Bilinear接触模型
Bilinear模型是库仑摩擦模型在有限元中的表现形式，库仑摩擦模型是目前塑性成形过程中常用的模型之一[9]，由 COULOMB 在AMONTONS 和 LEONARDO 的基础上，提出“摩擦力与作用在接触面上的正压力成正比，且与相对滑移速度无关”，进一步发展成库仑摩擦模型[10]。
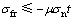(1)
式中：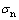
为接触点法向应力；
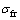为切向应力；
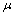为摩擦因数；t为相对滑动速度方向上的切向单位矢量。
当法向力给定后，摩擦力出现阶梯函数状变化，数值模拟计算中引入这种不连续性，往往会导致计算困难，因此，采用1个滑动面来消除这种这种不连续性，Bilinear模型图如图1所示。图1中：ft为剪切力；
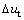为切向位移增量；
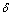为黏性极限距离。
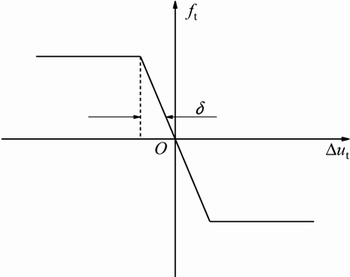
图1 Bilinear模型示意图
Fig. 1 Sketch map of Bilinear friction model
1.1.2 Stick-slip接触模型
Stick-slip接触模型是基于库仑摩擦模型的针对粘滑摩擦状态的修正模型，假设初始状态时处于黏结状态，经过一定切向位移转变为滑动摩擦状态，能够实现黏性摩擦到滑动摩擦的突变，如图2所示。图2中：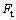
为摩擦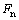力；
为法向力；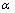
为乘子，一般取1.05；
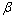为滑动摩擦到黏性摩擦的相对位移过度区域，一般取10-6。
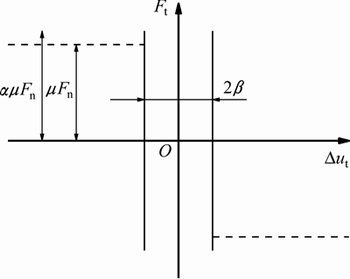
图2 Stick-slip模型示意图
Fig. 2 Sketch map of Stick-slip friction model
1.1.3 Glue模型
Glue接触模型将接触处理为始终黏结状态，在数值模型中表现为接触节点之间固连，没有相对位移产生。
1.2 本构模型
粉末致密化过程实质上是由非连续体转变为连续体的过程，在这个过程中体积不断发生变化。非连续体的变形非常复杂，需要考虑所有颗粒的应力与应变[6]，因此，将粉末看作“连续的多孔材料”，应用连续介质理论描述粉末体。
在经典Von Mises理论基础上，SHIMA等[11]考虑多孔材料相对密度和静水压力的影响，提出Shima屈服模型。
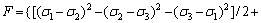
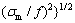(2)
式中：
，
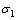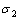和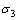
为3个主应力；f为静水压力对屈服的影响程度；
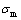为静水压力；F为屈服应力。
本文采用MSC.marc软件对成形过程进行模拟，软件中嵌入的是修正后的Shima模型：
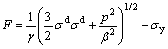(3)
式中：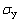
为单轴屈服应力；
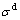为应力偏张量；p为静水压力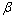；和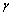
为相对密度的函数，
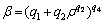(4)
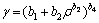(5)
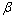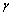单轴压缩试验可获得和与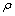
之前的关系数据，进而获得
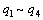和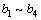
共8个系数的数值。
2 结果与分析
试验采用的Ti6Al4V预合金粉末由陕西海宝特种金属材料有限公司提供，粉末粒径在60~300 μm之内，包套材料为不锈钢。Ti6Al4V的化学成分如表1所示。
热等静压设备为ABB公司的QIH-5热等静压机，最高温度可达2 000 ℃，最高压力为200 MPa。包套材质为301不锈钢，厚度为2 mm。为保证粉末充填密实，充填过程在VSR-200时效振动系统上完成，振动频率为30 Hz，振动时间1 h，振动后粉末振实相对密度为0.65。为充分排出实验件内空气，在500 ℃下进行高温脱气8 h，使得包套内真空度达到10-5 Pa，随后，采用电子束焊密封包套。将已经脱气的包套进行热等静压压制，热等静压温度为920 ℃，压力为120 MPa，升温升压、保温保压、降温降压时间分别为2，3和2 h。
表1 Ti6Al4V合金粉末的化学成分(质量分数)
Table1 Chemical composition of Ti6Al4V aluminum alloy powders %
Ti6Al4V合金粉末试件为轴对称圆柱试件，所以选取模型的1/8为计算单元，利用大型有限元软件MSC.marc进行模拟计算，并将粉末试件相对密度的模拟计算结果与试验结果进行对比，结果如图3所示。
试验结果如图3(a)所示。在热等静压过程中，尽管包套外表面都处在等静压载荷作用下，但由于包套对压力具有屏蔽效应[12]，包套内部粉末则处在不等载荷的作用下，这也是试验件内部产生相对密度梯度的原因。这种屏蔽效应在包套和顶部直壁所组成的“L”状结构处尤为明显，因此，该区域相对密度较低。其他区域粉末收缩比较明显，致密化程度较高[13]。
由图3可以看出：Bilinear模型与Stick-slip模型得到的坯料变形规律与HIP试验结果高度相符，Glue模型对坯料边角处变形的预测结果与试验结果存在一定差距。在热等静压过程中，随着压力与温度上升，粉末体收缩，包套产生相应变形。采用Glue模型时，粉末与包套之间处于一种黏结状态，在伴随包套发生变形的同时，由于这种黏结效应，粉末产生一定程度的塑性变形；而对于Blinear模型与Stick-slip模型，粉末与包套处于摩擦接触状态，粉末与包套产生一定程度的相对滑动。Glue模型的这种粉末塑性变形对于外部等静压的阻碍作用远远大于摩擦力的阻碍作用，因此，这种阻碍作用是与包套变形程度直接相关的。在“L”状结构处，包套的变形程度较大，这种阻碍作用尤为明显。在其他区域，包套变形程度较低，阻碍作用较小。这也是3种模型在“L”状区域变形程度差异较大，而轴向与径向尺寸差异较小的主要原因。表2所示为采用3种不同接触模型的热等静压数值模拟结果与试验结果的对比。
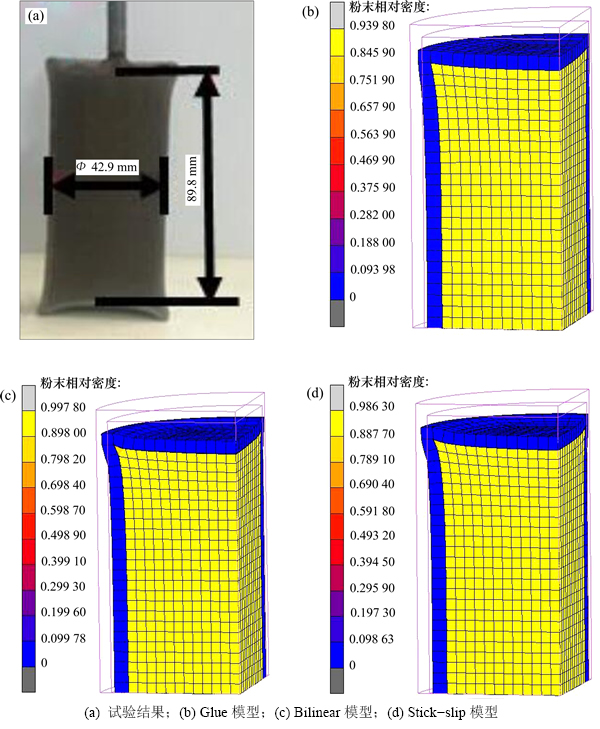
图3 相对密度试验及模拟结果图
Fig. 3 Test and simulation results of relative density
表2 参数模拟结果与试验结果的对比
Table 2 Comparison between simulation results and test result of parameters
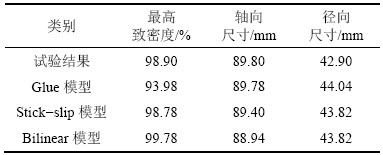
由表2可知：参数数值模拟结果和试验数据高度一致，最大相对误差不超过5%，在工程允许得误差范围之内，说明数值模拟在预测Ti6Al4V合金粉末热等静压致密化过程方面具有一定的指导意义。
2.1 粉固界面的接触理论分析
目前，还没有针对热等静压过程中粉固界面的接触理论研究，而针对粉末压实过程中粉固界面的接触研究较多，可采用压制过程的理论分析模型计算摩擦力[14]，而对于圆柱粉末热等静压件，由于包套外部受到等静压作用，而且在热等静压后，包套径向尺寸收缩仅为10%，因此，在粉末压制圆柱模型侧曲面施加等同于顶部平面的压力，这种修改后的力学状态等同于热等静压圆柱模型1/2结构的力学状态。由于热等静压圆柱件侧曲面整体上收缩程度基本保持一致，而平面将会出现中心凹陷等不均匀收缩，因此，这种理论应用仅局限于简单圆柱模型。可将圆柱粉末单向压实理论引入热等静压并针对热等静压受力、变形的特点进行修正补充。
圆柱粉末件的简化模型及受力状态如图4所示。图4中：Q为粉末体横截面积；h为1/2粉末体高度；p为热等静压的压强。从距离上表面z处取一厚度为dz薄层进行受力分析。由于圆柱体表面受到相等压力，圆柱体粉末与包套的接触状态关于中心面对称，因此，取1/2圆柱体进行研究。
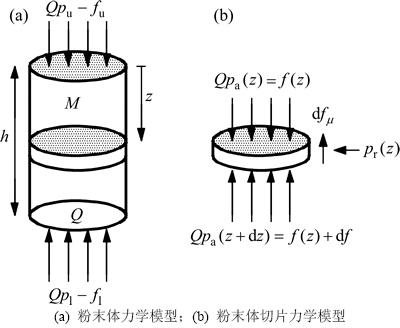
图4 粉末体受力示意图
Fig. 4 Force diagram of powder body
在热等静压过程中，粉体受力平衡。上表面所受到的压应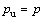力
，压力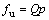
，因此，薄层上表面的轴向实际致密化力为
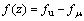(6)
式中：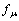
为包套与粉末之间的摩擦力。
轴向实际致密化力的增量为
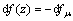(7)
摩擦力正比于径向压力，
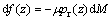(8)
式中：M为圆柱体的包络面面积。
考虑径向应力与轴向应力的比值，令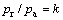
，代入式(8)得
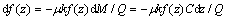(9)
式中：C为圆柱体在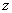
处的周长，由
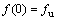，对式(9)进行积分得：
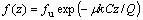(10)
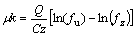(11)
k为径向压力与轴向压力的比值，它是材料和几何的相关参数。对于纯弹性圆柱体，进行轴向加载时，径向会产生膨胀，根据胡克定律有
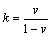(12)
但是，弹性变形不是热等静压过程中粉末致密化的主要机制，因此，由式(12)得到的固定值k不适用于热等静压。
粉末致密化过程是一个高度非线性化的过程，由于塑形变形是粉末致密化的主要机制，因此，可将塑形数学理论应用于粉末致密化。粉末压制已经采用该理论取得较好的结果[4]。针对粉末压制过程中所得k进行修正，可应用于热等静压过程中。
在粉末压制过程中，粉末在轴向进行压缩时，径向会产生膨胀的趋势，因此，粉末压制过程中的径向力就是抑制这种趋势而产生的力。而对于圆柱体热等静压，其径向尺寸在热等静压前后变化仅为10%，可近似采用粉末压制理论。包套轴向与径向受到相同的压力，粉末径向就受到膨胀产生的力和外部压力的双重作用，因此，可得热等静压过程中的k。
热等静压过程中的k为
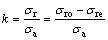(13)
式中：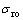
为外部压应力；
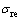为径向膨胀而产生的压应力。
由于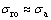
，因此，
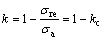(14)
式中：kc为粉末压制过程中的径向力与轴向力的比值。
根据式(14)及粉末压制过程中相关理论[4]，可获得热等静压过程中径向力与轴向力比值随相对密度的变化曲线，如图5所示。
在数值模拟中所给定的摩擦因数往往是一个固定值，为了探究粉固界面的实际摩擦因数，针对Stick-slip与Bilinear模型(Glue模型假设为固联状态，不存在摩擦)的数值模拟结果进行分析，将相关数据代入式(11)，得到摩擦因数随时间变化关系。由于降温降压阶段粉末已达到高度致密化状态，此时的接触为固体金属之间的接触，故只取升温升压阶段及保温保压阶段进行分析，如图6所示。
由图6可以看出：采用2种接触模型数值模拟结果所得实际摩擦因数差异较大；在升温升压阶段，采用Stick-slip模型所得实际摩擦因数具有较大初始值，并且随时间而降低，在4 000 s左右达到最小值，此时，粉末相对密度达0.9，粉末致密化过程基本完成；而采用Bilinear模型所得实际摩擦因数，其初始值较小，随着压力与温度升高而增加并在2 000 s达到最大值，然后出现下降趋势，并在5 000 s后趋于稳定；在保温保压阶段，这2种模型所得的实际摩擦因数基本稳定，采用Stick-slip模型的实际摩擦因数为0.15，采用Bilinear模型的实际摩擦因数为0.10。
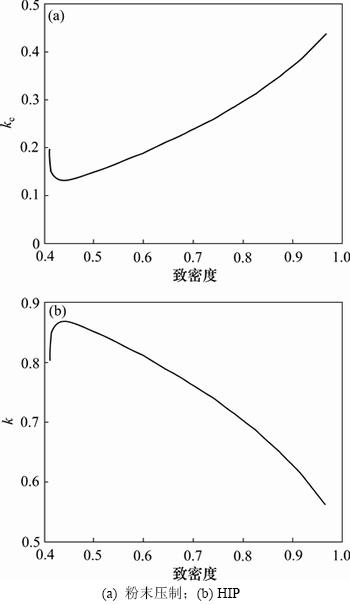
图5 径向力与轴向力比值
Fig. 5 Ratio of radial force to axial force
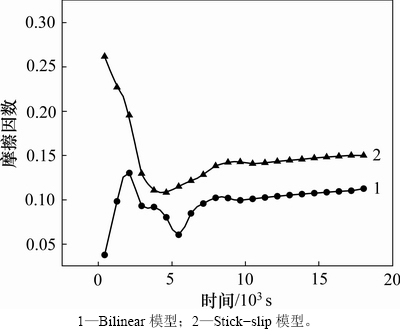
图6 实际摩擦因数
Fig. 6 Actual friction coefficient
粉固界面的摩擦状态是由两者之间的相互作用决定的，这种相互作用主要表现为粉末颗粒变形与滑移，在热等静压过程中是不断发生变化的。在热等静压前，粉末颗粒与包套的实际接触接近于点接触，因此，粉固界面总的真实接触面积非常小，当施加压力后，这些微小的接触区域便承受巨大的应力而发生黏附现象，使得热等静压起始时具有较高的摩擦因数[15]；随着压力的不断增加，粉末颗粒的接触面积不断增大，材料的硬化会产生一个更稳定的接触面[8]，进而粉末与模具之间的接触面上的孔隙逐渐被填平，使得接触面逐渐平滑，从而摩擦因数降低[16]。伴随着相对密度不断提高，粉末由松散颗粒转变为致密体，与包套的接触状态更接近于金属实体的接触，因而，在保温保压阶段摩擦因数趋于1个定值。2个模型在升温升压阶段的结果差异较大，升温升压阶段粉末相对密度较低。而当粉末相对密度较低时，粉末滑移可被看作粉末在靠近包套的边界层中的剪切作用以及在粉固界面上的滑动，这个过程有助于粉末在热等静压早期阶段的颗粒重排，并且对于复杂结构的成形起着重要的作用。因此，综合根据以上分析，Stick-slip接触模型能更好地反映出摩擦因数的变化过程。
2.2 接触模型对相对密度的影响
由表2可以看出3种模型均能实现对整体几何尺寸的预测。对于粉末制品来说，其最终整体成形密度与硬度、疲劳强度、韧性等性能密切相关，而密度分布的均匀性与缺陷、裂纹等因素密切相关，这些因素的存在甚至会导致热等静压件因性能低劣而废弃[16]。因此，在可靠预测几何尺寸的前提下，预测最终密度的准确度显得尤为重要。在预测最高相对密度方面，Stick-slip模型与Bilinear模型均能实现精准预测，而Glue模型预测效果较差。下面选取几个典型位置的相对密度预测进行分析，各节点位置如图7所示。
热等静压一般用于制造轮廓复杂的零件，节点A位于粉末体外沿，位于粉末体外廓急剧变化的部位，能够代表复杂结构部位粉末相对密度的变化趋势；节点B位于粉末体中心位置，能够代表内部粉末相对密度的变化趋势。
节点A和B处相对密度随时间变化的曲线如图8所示。从图8可知：2个位置的相对密度都是呈现上升趋势，但在热等静压初期，相对密度有下降趋势，这是由于随着温度上升，粉末体膨胀而产生的膨胀量大于压力产生的压缩量；随着压力的升高，压缩量越来越大，相对密度逐渐上升。
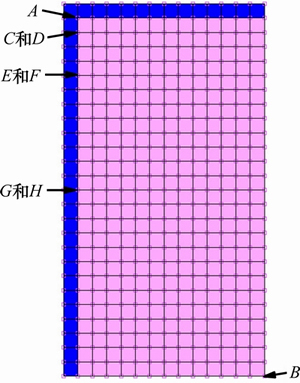
图7 FEM模型的节点位置
Fig. 7 Nodes positions in FEM model
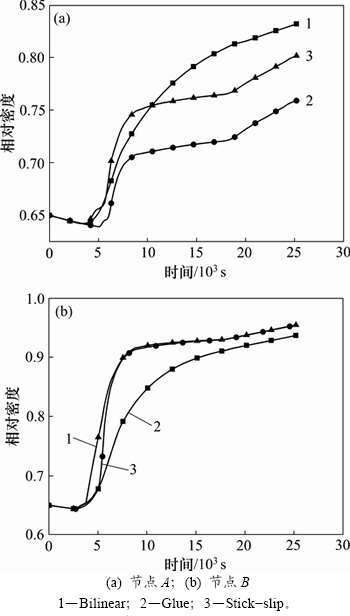
图8 热等静压过程中相对密度变化
Fig. 8 Relative density changes in HIP
热等静压完成后，这3种模型均能准确预测节点B处的相对密度变化趋势以及最终相对密度。而对于节点A处最终相对密度的预测结果，Glue模型仅为0.75，Stick-slip模型为0.80，Bilinear模型为0.83。在节点A区域进行取样，并采用阿基米德排水法[17]测得相对密度为0.88，因为由节点A附近区域的相对密度均比节点A的高，因此，测得值稍高于实际值。材料相对密度决定着材料的静态强度、塑性、动态强度、硬度等各项性能，而在相对密度为0.75时，对照相应实验曲线[18]，平面应力、抗拉强度、伸长率等参数均显著低于正常值，此时，Ti6Al4V合金粉末未完全致密化，这与实际情况是不相符的。热等静压多用于制备轮廓复杂零件，数值模拟对于以节点A为代表的结构急剧变化位置的预测准确性显得尤为重要。由此可见，Glue模型所预测的最终相对密度与实际情况存在较大误差。
2.3 接触模型对粉末体、包套之间相对位移的影响
包套与粉末体的相对位移对于外轮廓的形状变化具有一定影响作用，在热等静压中，存在着包套与坯料的相对位移过大而导致包套破裂的问题，通过对相对位移的预测能在一定程度上避免出现上述情况。包套与粉末体相对位移受到压力、温度、热膨胀系数差异等多方面的影响，由节点C和D，E和F，G和H之间的径向位移差得到相对位移，如图9所示。从图9可知：粉末体外沿的相对位移较大。因此，取节点C和D在3种模型下的数值模拟结果进行分析，如图10所示。
总体来看，Glue模型不能预测相对位移；Stick- slip模型与Bilinear模型的预测结果均呈现上升趋势并最终趋于稳定；在HIP升温升压阶段，Bilinear模型与Stick-slip模型预测的相对位移出现明显上升趋势，粉末的致密化主要发生在这个阶段，相对位移的这种变化趋势主要是粉末致密化的作用结果。在保温保压阶段，相对位移趋于稳定，主要是由于这个阶段发生蠕变，粉末体相对密度变化较小[19]。在降温降压阶段，Stick-slip模型预测的相对位移出现了上升趋势，在降温降压阶段，由于粉末材料与包套材料热膨胀系数不同，当温度下降相同时产生的收缩量不同，从而导致一定相对位移的产生。因此，Glue模型不能预测相对位移，Stick-slip与Bilinear模型预测的最终相对位移基本一致，Stick-slip模型能更好地反映相对位移的具体变化趋势。
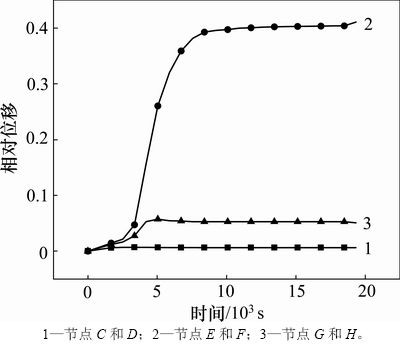
图9 相对位移随时间变化
Fig. 9 Variation of relative displacement with time
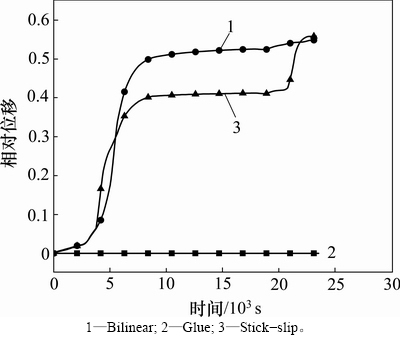
图10 节点C和D相对位移
Fig. 10 Relative displacement between node C and D
3 结论
1) 基于Shima模型的有限元技术在预测Ti6Al4V合金热等静压零件变形以及相对密度方面具有较高的精度，径向尺寸、轴向尺寸、相对密度的相对误差均在5%以内。因此，数值模拟可以为热等静压零件成形提供参考依据，实现精确控形。
2) 粉固界面之间的摩擦因数处于一个复杂变化的过程。初始阶段摩擦因数最大，随着粉末的致密化而逐渐减小，最终趋于1个稳定值。Stick-slip模型能反映出这个变化趋势，初始摩擦因数为0.27，稳定摩擦因数为0.15。
3) Bilinear模型与Stick-slip模型能够准确预测相对密度变化趋势及数值；Glue模型不能预测相对位移，Stick-slip模型能够预测降温降压阶段相对位移的具体变化趋势。
参考文献：
[1] 金和喜, 魏克湘, 李建明, 等. 航空用钛合金研究进展[J]. 中国有色金属学报, 2015, 25(2): 280-292.
JIN Hexi, WEI Kexiang, LI Jiangming, et al. Research development of titanium alloy in aerospace industry[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(2): 280-292.
[2] 郎利辉, 王刚, 布国亮, 等. 钛合金粉末热等静压数值模拟及性能研究[J]. 粉末冶金工业, 2015, 25(3): 1-6.
LANG Lihui, WANG Gang, BU Guoliang, et al. Study of numerical simulation and mechanical properties of hot isostatic pressed titanium alloy powder[J]. Powder Metallurgy Industry, 2015, 25(3): 1-6.
[3] 马福康. 等静压技术[M]. 北京: 冶金工业出版社, 1992: 175-177.
MA Fukang. Isostatic pressing technology[M]. Beijing: Metallurgical Industry Press, 1992: 175-177.
[4] WIKMAN B, SOLIMANNEZHAD N, LARSSON R, et al. Wall friction coefficient estimation through modeling of powder die pressing experiment[J]. Powder Metallurgy, 2000, 43: 132-138.
[5] 王冰, 纪玮, 邓太庆, 等. TA15粉末冶金产品热等静压成形工艺过程的数值模拟[J]. 宇航材料工艺, 2017, 47(4): 19-22.
WANG Bing, JI Wei, DENG Taiqing, et al. Numerical simulation of hot isostatic pressing for TA15 titanium alloy powder product[J]. Aerospace Materials & Technology, 2017, 47(4): 19-22.
[6] 王刚. 轻质高强度材料热等静压成形关键技术及组织性能分析[D]. 北京: 北京航空航天大学机械工程及自动化学院, 2016: 3-5.
WANG Gang. Study on microstructure-property and key technologies of hot isostatic pressing on high strength and light weight materials[D]. Beijing: Beihang University. School of Mechanical Engineering and Automation, 2016: 3-5.
[7] 刘国承, 史玉升, 魏青松, 等. 316L粉末热等静压致密化过程数值模拟[J]. 华中科技大学学报(自然科学版), 2011, 39(10): 23-27.
LIU Guocheng, SHI Yusheng, WEI Qingsong, et al. Numerical simulation of the densification of 316 powder during hot isostatic pressing[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(10):23-27.
[8] 瞿宗宏, 刘建涛, 张国星, 等. FGH4097合金热等静压成形数值模拟[J]. 材料热处理学报, 2017, 7(7): 173-179.
QU Zonghong, LIU Jiantao, ZHANG Guoxing, et al. Numerical simulation of hot isostatic pressing process of FGH4097 superalloy[J]. Transactions of Materials and Heat Treatment, 2017, 7(7): 173-179.
[9] CORA O N. Friction analysis in cold forging[D]. Ankara: Middle East Technical University. Graduate School of Natural and Applied Science, 2004: 5-7.
[10] 孙丹丹, 陈火红. 全新Marc实例教程与常见问题解析[M]. 2版. 北京: 中国水利水电出版社, 2016: 195-200.
SUN Dandan, CHEN Huohong. New Marc instance tutorials and FAQ[M]. 2nd ed. Beijing: China Water & Power Press, 2016: 195-200.
[11] SHIMA S, OYANE M. Plasticity theory for porous metals[J]. Mechanical Science, 1976, 18(6): 285-291.
[12] 郎利辉, 王刚, 黄西娜, 等. 包套在铝合金粉末热等静压成形中的屏蔽效应及其对性能的影响[J]. 中国有色金属学报，2016, 26(2): 261-271.
LANG Lihui, WANG Gang, HUANG Xina, et al. Shielding effect of capsules and its impact on mechanical properties of P/M aluminium alloys fabricated by hot isostatic pressing[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(2): 261-271.
[13] 郎利辉, 续秋玉, 张东星, 等. 钨合金粉末的热等静压数值模拟及验证[J]. 粉末冶金材料科学与工程, 2014, 19(6): 839-846.
LANG Lihui, XU Qiuyu, ZHANG Dongxing, et al. Numerical simulation and verification of tungsten alloy powders during hot isostatic pressing[J]. Materials Science and Engineering of Powder Metallurgy, 2014, 19(6): 839-846.
[14] ERNST E, BARNEKOW D. Pressure, friction and density during axial powder compaction[J]. Metal Powder Report, 1995, 50(1): 1-3.
[15] 孟丽芬, 胡成亮, 赵震. 金属塑性成形中摩擦模型的研究进展[J]. 模具工业, 2014, 40(4): 1-7.
MENG Lifen, HU Chengliang, ZHAO Zhen. Research progress of friction model in metal plastic forming[J]. Die & Mould Industry, 2014, 40(4): 1-7.
[16] 王德广. 金属粉末高致密化成形及其数值模拟研究[D]. 合肥: 合肥工业大学材料科学与工程学院, 2010: 23-36.
WANG Deguang. Research on high densification and numerical simulation of metal powder compaction processes[D]. Hefei: Hefei University of Technology. School of Materials Science and Engineering, 2010: 23-36.
[17] 黄俊, 薛鹏举, 魏青松, 等. TiAl4V合金整体零件的两步热等静压近净成形工艺探究[J]. 中国机械工程, 2015, 26(18): 2539-2544.
HUANG Jun, XUE Pengju, WEI Qingsong, et al. Research on near-net-shaping TiAl4V alloy parts under two-step hot isostatic pressing[J]. China Mechanical Engineering,2015, 26(18): 2539-2544.
[18] 黄培云. 粉末冶金原理[M]. 2版. 北京: 冶金工业出版社, 2017: 377-390.
HUANG Peiyun. Powder metallurgy principle[M]. 2nd ed. Beijing: Metallurgical Industry Press, 2017: 377-390.
[19] 段文. 粉末致密化理论及铝合金材料参数反向建模研究[D]. 北京: 北京航空航天大学机械工程及自动化学院, 2017: 9-12.
DUAN Wen. Powder densification theory and reverse modeling of aluminum alloy[D]. Beijing: Beihang University. School of Mechanical Engineering and Automation, 2017: 9-12.
(编辑 杨幼平)
收稿日期：2018-03-26；修回日期：2018-05-07
基金项目(Foundation item)：国家自然科学基金资助项目(51675029) (Project(51675029) supported by the National Natural Science Foundation of China)
通信作者：郎利辉，博士，教授，从事粉末热等静压研究；E-mail: lang@buaa.edu.cn
