岩石中浅孔爆破特性的数值模拟
李云,刘霁
(湖南城市学院 土木工程学院,湖南 益阳,413000)
摘要:采用某工程现场岩石力学、爆破参数,建立柱状装药、微差爆破数值计算模型,研究岩石中浅孔爆破应力特征和速度变化规律,考虑介质的重力、分段爆破影响。研究结果表明:最大主应力在几何形状变化处最大;有效应力最大值出现在距离爆源最近处;速度计算结果与现场爆破振动速度监测结果相吻合。
关键词:岩石;浅孔爆破;爆破特性;数值模拟
中图分类号:TD235.4 文献标志码:A 文章编号:1672-7207(2012)04-1519-04
Numerical simulation on mechanical properties of shallow-hole blasting in rocks
LI Yun, LIU Ji
(College of Civil Engineering, Hunan City University, Yiyang 413000, China)
Abstract: Using the rock mechanics and blasting parameters in a certain field engineering, the numerical calculation model of cylindrical charge and segmented blasting was built, and the stress features and velocity laws in the shallow-hole blasting were researched. The factors of gravity for the medium and sub-blasting effect were considered.The results show that the effective stresses of geometry shape diversification are maximum, and the maximum principal stresses of the nearest station from the explosion source are maximum.The computation velocities are in good agreement with those obtained by monitoring vibration.
Key words: rocks; shallow-hole blasting; blasting properties; numerical simulation
在岩土工程爆破时,由于成本和环境、设备等因素的限制,不可能对爆破施工中的各个参数全部监测,从而限制了对爆破机理的深入研究。目前,人们对岩石中爆破力学特性进行了大量研究,如浦锡锋等[1]运用BCM模型对岩石中爆炸应力波传播、岩石破碎过程进行了模拟;龚敏等[2]运用FRLAC/ FLAC3D程序动力分析模块研究爆破作用下岩体累积损伤效应及其稳定性;王礼立[3]利用ADINA计算程序对岩体内爆炸应力波能进行计算分析;宇文惠鑫[4]使用ABAQUS/Explicit软件对岩石爆破的动力学行为进行了三维弹塑性碎裂有限元数值模拟;夏祥[5]用离散元软件UDEC计算得到爆破荷载作用下的岩体振动特征和衰减规律等。这些研究大部分集中于对爆破后的效果进行分析,简化了装药结构,数值模拟结果没有得到现场验证,影响了计算结果的可靠性。目前,国内使用较多的爆破模拟程序是LS-DYNA程序,它是1个显示非线性动力分析通用的有限元程序,可以求解各种二维、三维爆炸动力响应问题,其优势在于可以从时间和空间2方面描述爆破力学的特征[6-9]。在此,本文作者利用LS-DYNA程序,按实际工程的柱状、多孔装药模拟岩石中爆破力学的特性分析爆破的 本质。
1 数值计算模型
1.1 岩体力学模型
根据试验现场情况,将岩体本构模型简化成连续介质模型。岩石的应力-应变关系呈现复杂的非线性特征,在达到屈服极限之前将介质近似地视为弹性体,达到屈服极限后视为塑性体,数值模拟采用常用的各向同性-弹塑性材料(即MAT_PLASTIC_ KINEMATIC材料)[10-12],其屈服条件为:
 (1)
(1)
式中: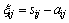 ;
;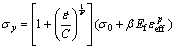 ;sij为柯西应力张量;F和C为输入常数;σ0和β分别为初始屈服应力和硬化参数;
;sij为柯西应力张量;F和C为输入常数;σ0和β分别为初始屈服应力和硬化参数; 为应变率,
为应变率,
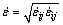 ;Ef为塑性硬化模量,
;Ef为塑性硬化模量,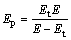 ;E为
;E为
弹性模量;Et为切线模量;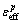 为有效塑性应变。
为有效塑性应变。
本文在DYNA程序中嵌入各向同性—弹塑性材料模型进行分析,所取岩石力学参数来源于现场试验,见表1。
1.2 爆破荷载状态方程
炸药选用岩石乳化炸药,采用专用的考虑爆生气体的爆破荷载模型(炸药状态方程JWL)模拟炸药爆轰过程中压力和比容关系[13-15]:
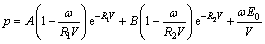 (2)
(2)
式中:p为爆轰产物压力,GPa;A和B为炸药材料相关参数,GPa;R1,R2和ω为炸药材料常系数;V为相对体积;E0为初始化比内能,GPa,其参数见表2。
1.3 浅孔爆破数值模型的建立
爆破孔的布置如图1所示。炸药分3段进行起爆,模型上部模拟实际地形情况进行表层土和岩体的建模,模型单元类型为Solidl64,炮孔直径为2 m,炮孔深为2.2 m,填塞长度为40 cm。在建模过程中,分别对岩石、炸药、表土层和填塞物4种不同材质划分不同网格,计算模型的节点数为196 956,单元数为 179 476,网格模型见图2。模型2中边竖直边界以及底边边界为无反射边界,以减小边界应力波反射的影响,顶面根据实际情况为自然边界,反映爆源周围岩体的实际受力状态。根据试验测量的数据,爆破应力、速度等参数衰减速率很快,模拟的求解时间设置为0.1 s,以便观察爆炸应力波传播的整个运动过程。
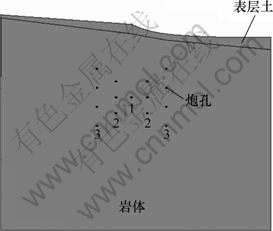
图1 模型正视图
Fig.1 Front view of model
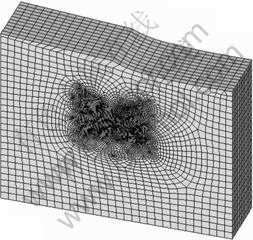
图2 DYNA网格模型
Fig.2 DYNA mesh model
表1 岩石主要参数
Table 1 Parameters of rock used in calculation

表2 乳化炸药材料及其状态方程参数
Table 2 Parameters of emulsion explosive and state equation

2 数值模拟结果分析
微差爆破有利于减小爆破危害,提高炸药的利用效率。以往研究未考虑微差爆破对爆破的影响,该模型按实际爆破段与段之间的微差时间设置为25 ms进行计算,模型同时考虑介质的重力因素影响,爆破后总的应力云图见图3(微差时间t为0.798 ms)和图4(微差时间t为25.400 ms)。
有效应力反映的是岩体内单位面积上固体颗粒承受的平均法向力。最大主应力为正应力和剪应力的矢量和,所以,最大主应力可用来描述结构的实际受力情况。表3所示为不同位置单元有效应力与最大主 应力。

图3 微差时间为0.798 ms时的爆炸应力云图
Fig.3 Stress nephogram of blasting when t=0.798 ms
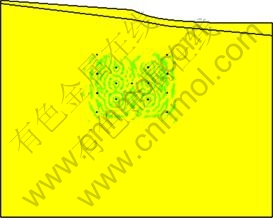
图4 微差时间为25.400 ms时的爆炸应力云图
Fig.4 Stress nephogram of blasting when t=25.400 ms
表3 单元有效应力与最大主应力
Table 2 Parameters of effective stress and maximum principal stress
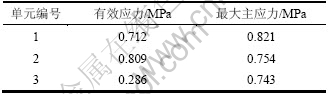
单元1对应斜坡位置质点,单元2对应埋深较浅处节点,单元3对应埋深较深处质点。由于岩石几何形状的突变,引起轻微的应力集中现象,单元1最大主应力最大。有效应力反映了颗粒间作用力,由于单元2距离爆源最近,故其有效应力最大。
3 数值模拟结果检验
目前,现场爆破参数主要是爆破振动速度,本文利用现场爆破振动速度监测结果检验数值模拟结果的正确性。图5所示为地表不同位置速度曲线,节点7040对应埋深较浅位置质点,节点7020对应斜坡处节点,节点7290对应埋深较深处质点。现场对爆破振动监测结果表明:斜坡处速度比埋深深的一侧速度大,埋深较浅的一侧速度最大,数值模拟结果与实际结果相 吻合。
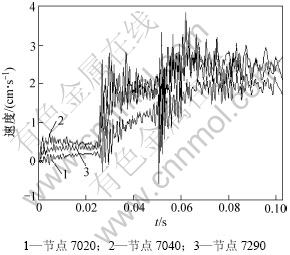
图5 不同位置速度曲线
Fig.5 Velocity curves of different positions
4 结论
(1) 利用现场的爆破参数建立岩石中浅孔爆破数值分析模型,从时间和空间上较好地反映了爆破力学特性。最大主应力在几何形状变化处最大;有效应力最大值出现在距离爆源最近处。
(2) 爆破各应力对岩体的影响随其特性不同而变化,根据数值模拟进行爆破力学特性研究具有其优越性。由速度分布特征对比,数值模拟结果与现场测试结果相吻合。
参考文献:
[1] 浦锡锋, 张海波, 田宙, 等. 岩石中强爆炸动力学过程数值模拟[J]. 岩石力学与工程学报, 2005, 24(1): 405-407.
PU Xi-fang, ZHANG Hai-bo, T1AN Zhou, et al. Numerical simulation of underground explosion in granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 405-407.
[2] 龚敏, 黄毅华, 王德胜, 等. 松软煤层深孔预裂爆破力学特性的数值分析[J]. 岩石力学与工程学报, 2008, 27(8): 1674-1677.
GONG Min,HUANG Yi-ua,WANG De-heng, et al. Numerical simulation on mechanical characteristics of deep-hole preprinting blasting in soft coal bed[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1674-1677.
[3] 王礼立. 爆炸力学数值模拟中本构建模问题的讨论[J]. 爆炸与冲击, 2003, 23(2): 106-108.
WANG Li-li. On constitutive modeling in numerical simulation of explosion mechanics[J]. Explosion and Shock Waves, 2003, 23(2): 106-108.
[4] 宇文惠鑫. 炮孔双介质不耦合装药断裂控制爆破理论研究与数值模拟[D]. 太原: 太原理工大学矿业工程学院, 2006: 47-65.
YUWEN Hui-xin. Numerical simulation and theory study of blasthole fracture controlled blasting with two decoupling interaction charge[D]. Taiyuan: Taiyuan University of Technology. College of Mining Technology, 2006: 47-65.
[5] 夏祥. 爆破荷载作用下岩体振动特征的数值模拟[J]. 岩土力学, 2005, 6(1): 50-54.
XIA Xiang. Udec modeling of vibration characteristics of jointed rock mass under explosion[J]. Rock and Soil Mechanics, 2005, 26(1): 50-54.
[6] 罗伟, 朱传云, 祝启虎. 隧洞光面爆破中炮孔堵塞长度的数值分析[J]. 岩土力学, 2008, 29(9): 2487-2490.
LUO Wei, ZHU Chuan-yun, ZHU Qi-hu. Numerical simulation of stemming length in tunnel smooth blasting[J]. Rock and Soil Mechanics, 2008, 29(9): 2487-2490.
[7] 刘军, 刘汉龙, 张正珺. 爆炸荷载下土石坝动力响应特征的数值模拟[J]. 防灾减灾工程学报, 2010, 30(1): 10-13.
LIU Jun, LIU Han-long, ZHANG Zheng-jun. Numerical simulation of dynamic response of an earth and rock-fill dam to a blast loading[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(1): 10-13.
[8] 边金, 陶连金, 郭军. 浅埋地下结构和土层在动荷载作用下的反应分析[J]. 世界地震工程, 2005, 21(4): 49-52.
BIAN Jin, TAO Lian-jin, GUO Jun. Dynamic response of the underground structure and soil[J]. World Earthquake Engineering, 2005, 21(4): 49-52.
[9] 尚晓江, 苏建宇, 王化锋. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 北京: 中国水利水电出版社, 2008: 10-20.
SHANG Xiao-jiang, SU Jian-yu, WANG Fa-feng. ANSYS/LS-DYNA dynamic analysis methods and projects[M]. Beijing: China Water Power Press, 2008: 10-20.
[10] 王志亮, 郑明新. 基于TCK损伤本构的岩石爆破效应数值模拟[J]. 岩土力学, 2008, 29(1): 230-233.
WANG Zhi-liang, ZHENG Ming-xin. Numerical simulation of effect of rock blasting based on TCK damage constitutive model[J]. Rock and Soil Mechanics, 2008, 29(1): 230-233.
[11] 夏昌敬, 鞠杨, 谢和平. 爆炸波在岩体巷道中传播和能量耗散的数值分析[J]. 弹道学报, 2005, 17(4): 1-4.
XIA Chang-jing, JU Yang, XIE He-ping. Numerical analysis of propagation of explosion wave and energy dissipation in tunnel and surrounding rock mass[J]. Journal of Ballistics, 2005, 17(4): 1-4.
[12] 曲志明, 周心权, 巩伟平. 大爆破爆炸冲击波在破碎岩体间传播的数值模拟研究[J]. 振动与冲击, 2007, 26(12): 60-64.
QU Zhi-ming, ZHOU Xin-quan, GONG Wei-ping. Numerical simulation on shock wave propagation in crushed rocks during interns blasting[J]. Journal of Vibration and Shock, 2007, 26(12): 60-64.
[13] 高富强. 最大水平主应力对巷道围岩稳定性影响的数值分析[J]. 矿业研究与开发, 2008, 28(1): 62-65.
GAO Fu-qiang. Numerical analysis on the influence of maximum horizontal principal stress on surrounding rock stability of roadway[J]. Mining Research and Development, 2008, 28(1): 62-65.
[14] 夏祥, 李俊如, 李海波, 等. 爆破荷载作用下岩体振动特征的数值模拟[J]. 岩土力学, 2005, 26(1): 50-54.
XIA Xiang, LI Jun-ru, LI Hai-bo, et al. Under modeling of vibration characteristics of jointed rock mass under explosion[J]. Rock and Soil Mechanics, 2005, 26(1): 50-54.
[15] Bakhshandeh A H, Mozdianfard M R, Siamaki A. Predicting of blasting vibrations in Sarcheshmeh copper mine by neural network[J]. Safety Science, 2010, 48: 319-325.
(编辑 陈灿华)
收稿日期:2011-05-07;修回日期:2011-07-25
基金项目:湖南省科技计划项目(2011SK3128)
通信作者:李方(1975-),女,湖北孝感人,讲师,从事土木工程智能建筑的教学和研究;电话:13507376571;E-mail:liyunliuji@163.con