Comparison of evolution laws of stress and strain fields in hot rolling of titanium alloy large rings with different sizes

WANG Min^{1, 2}

1. Department of Materials Engineering, Hubei University of Automotive Technology, Shiyan 442002, China;

2. College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China

Received 22 July 2010; accepted 29 March 2011

Abstract: For hot rolling of titanium alloy large rings, evolution laws of stress and strain fields in rings with various sizes were explored and compared based on a reliable coupled thermo-mechanical three-dimensional (3D) finite element (FE) model. The results show that for forming processes of different rings, as 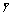(the equivalent distribution ratio of feed amount per revolution of a process) decreases, the final peak Mises stress may transfer from the biting point at the driver roll side to that at the idle roll side, and the final peak equivalent plastic strain may transfer from the outside surface to the inside surface; as 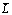(the equivalent deformation zone length of a process) increases, the final peak Mises stress may appear in the middle layer. The final positions of peak Mises stress and equivalent plastic strain are the combined effects of the above two aspects. In the deformation zone of a deformed ring, the surface layers are in the 3D compressive stress state, while the middle layer is in the 1D compressive and 2D tensile stress state or 2D compressive and 1D tensile stress state; the whole ring is in the 1D compressive and 2D tensile strain state.

Key words: titanium alloy; hot rolling of large rings; stress and strain; modeling and simulation; finite element

1 Introduction

The rapidly growing areas of high-tech such as aviation, aerospace and automobile urgently need to study the theory and technology of hot rolling of large rings, since this technology is capable of manufacturing large seamless annular components with high quality, low costs, short cycle and reduced emission. Moreover, research on the process is not only an important subject in the frontier of the advanced plastic forming field, but also an inevitable trend of large ring fabrication technique towards advanced plastic forming technology [1-2].

Large rings are of wide variety, small quantity, long production cycle and high costs relative to small ones, and successful manufacture in one time is pressingly required [3]. However, because few insights have been gained with respect to the evolution laws of crucial field variables such as stress and strain fields in rings during hot rolling of large rings, rings are prone to defecting such as crack and nonuniform microstructure in practice, which seriously affects manufacturing qualified products in one time. Especially, in order to realize light weight, high strength, high heat resistance and corrosion resistance of products, aviation and space industries have an increasing demand for large rings made of hard wrought material such as titanium alloy, which causes defects to be more sensitive to forming conditions and consequently, the above problem becomes more severe. Therefore, an in-depth understanding of the evolution laws of stress and strain fields in rings during hot rolling of large rings is of important significance for predicting defects and improving forming quality of products. However, the process is a highly nonlinear problem characterized by 3D incremental deformation, non- steady state, asymmetry and coupled thermo-mechanical effect, so analytic solution and experiments are unable to obtain stress and strain fields effectively. In contrast, computer modeling and simulation cannot only realize virtual forming, but also offer accurate and comprehensive stress and strain fields, and has became a power tool for plastic forming products development with high quality, low costs, short cycle and novelty [1, 4-5].

Until now, some studies have been conducted regarding stress and/or strain fields in ring rolling. XU et al [6] obtained the strain distribution in a rectangular ring after cold ring rolling by the visioplasticity method. SONG et al [7] investigated stress and strain distributions after hot rolling of an IN718 ring using a coupled thermo-mechanical FE method combined with a plane strain assumption. UTSUNOMIYA et al [8] analyzed the characteristics of stress and strain fields in cold rolling of a steel ring with rectangular section based on a plane strain FE method. WANG et al [9] employed the dynamic explicit software LS-DYNA to simulate hot rolling of steel and titanium alloy profiled rings, and obtained stress and strain distributions in final rings. KIM et al [10] simulated the strain distributions in the deformation zone of an alloy steel ring at a given moment using 3D FE models for hot rolling of profiled large rings. However, these researches are generally only concerned with either stress and strain fields at a certain moment or a specific ring. It appears that there have not been any sufficient analysis and comparison of evolution laws of stress and strain fields in different rings during the whole process. Therefore, taking hot rolling of titanium alloy large rings as object, the present work analyzes and compares evolution laws of stress and strain fields in rings with various sizes using a reliable coupled thermo-mechanical 3D FE model.

2 Related theoretical principle of ring rolling

2.1 Ratio of feed amount per revolution

The ratio of feed amount per revolution at the driver roll side to that at the idle roll side, γ [11], and its equivalent value over the total forming time, 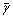 [12], can be calculated by

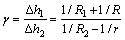                        (1)

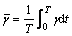                                (2)

where Δh₁ and Δh₂ are the feed amounts per revolution at the driver roll side and at the idle roll side, respectively; R₁ and R₂ are the radii of the driver roll and idle roll, respectively; R and r are the outer and inner radii of the deforming ring, respectively; T is the total forming time; and t is the time.

2.2 Deformation zone length

The deformation zone length, L [12], and its equivalent value over the total forming time, 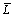, can be obtained by

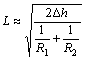                              (3)

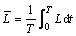                                (4)

where Δh is the feed amount per revolution. The relationship between Δh and forming parameters can be expressed by [11]

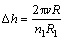                                 (5)

where n₁ is the rotational velocity of the driver roll and v is the feed rate of the idle roll.

3 FE model and simulation conditions

Adopting the FE modeling method for hot ring rolling [4], a coupled thermo-mechanical 3D FE model for hot rolling of Ti-6Al-4V titanium alloy large rings was developed based on ABAQUS/Explicit, as illustrated in Fig. 1. The model has been validated by comparison with experimental results in terms of surface temperature and geometry histories [12]. Based on the model, evolution laws of stress and strain fields in rings with various sizes will be examined and compared. The simulation conditions are summarized in Table 1.

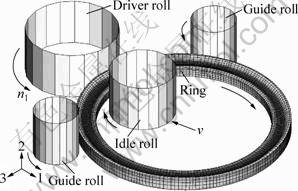
Fig. 1 Coupled thermo-mechanical 3D FE model for hot rolling of titanium alloy large rings

4 Results and discussion

4.1 Stress field

Hot ring rolling pertains to local incremental forming technologies, so the stress in the deformation zone is much greater than that outside the deformation zone. The study focuses on the stress field in the deformation zone. Figure 2 shows contours of Mises stress field in ring 1 at different time. It can be seen from Figs. 2(a) and (b) that at the early stage, the peak stress appears at the biting point at the driver roll side (index A), the stress at the biting point at the idle roll side (index B) is smaller, and the minimum stress exists in the middle layer (index C). With the process progressing, the distance between the two biting points shortens, the peak stress transfers to the biting point at the idle roll side, and the stress in the middle layer becomes larger and larger, as shown in Figs. 2(c) and (d). This variation can be explained as follows. According to Eq. (1), γ decreases monotonely with time, which indicates that the feed amounts per revolution at the driver roll side decreases relative to that at the idle roll side. As a result, the peak stress transfers from the biting point at the driver roll side to that at the idle roll side. On the other hand, for constant v and n₁, Δh increases with time by Eq. (5), so L increases by Eq. (3). Meanwhile, the radial thickness of ring 1 decreases. These two aspects imply that the plastic penetration along the radial direction of the ring is enhanced, and thus the deformation in the middle layer increases, leading to increased stress in the middle layer. It can also be found from Fig. 2 that the peak stress increases (Figs. 2(a) and (b)) and then decreases (Figs. 2(c) and (d)). This is because the plastic penetration of the ring is enhanced on the one hand, on the other hand the heat generation from plastic deformation causes the temperature of the ring to rise, resulting in the deformation resistance of metal decreasing, which is particularly true for titanium alloy owing to low heat conductivity.

Table 1 Simulation conditions

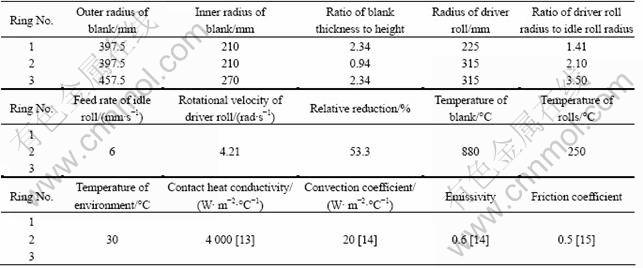
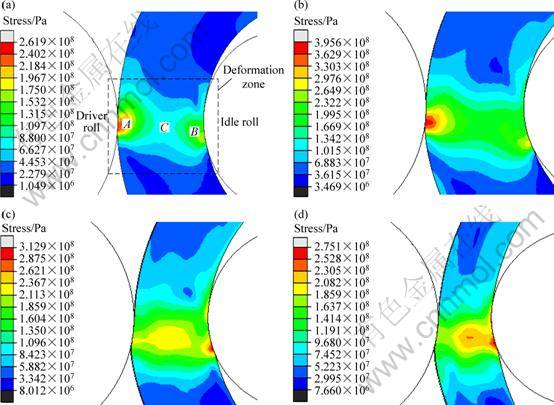
Fig. 2 Contours of Mises stress field in ring 1 at different time: (a) 0.67 s; (b) 1.67 s; (c) 9.67 s; (d) 16.67 s

Contours of Mises stress fields in ring 2 and ring 3 at different time are shown in Fig. 3 and Fig. 4, respectively. From Fig. 3, ring 2 has a similar stress distribution to ring 1(Figs. 3(a) and (c)), but at the later stage, the peak stress transfers from the biting point at the idle roll side to the middle layer(Fig. 3(d)). It is observed from Fig. 4 that at the early stage, both the biting points of ring 3 have larger stress (Figs. 4(a) and (b)), but at the later stage, the middle layer has the peak stress (Figs. 4(c) and (d)). The discrepancy between the three rings may arise from the following two aspects. First, 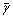 decreases in turn from ring 1 to ring 3 by Eq. (2). This demonstrates that from ring 1 to ring 3, the feed amount at the driver roll side decreases while that at the idle roll side increases, so at the early stage, ring 3 also has large stress at the biting point at the idle roll side, which is different from ring 1 and ring 2. Second,  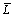increases in turn from ring 1 to ring 3 by Eq. (4), which indicates that the plastic penetration is improved, leading to increased deformation in the middle layer and consequently, ring 2 and ring 3 have the peak stress in the middle layer at the later stage.

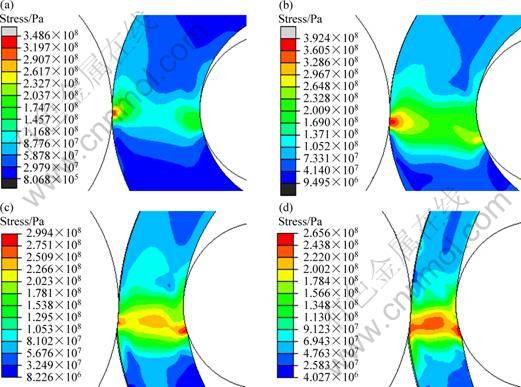
Fig. 3 Contours of Mises stress field in ring 2 at different time: (a) 0.67 s; (b) 1.67 s; (c) 9.67 s; (d) 16.67 s

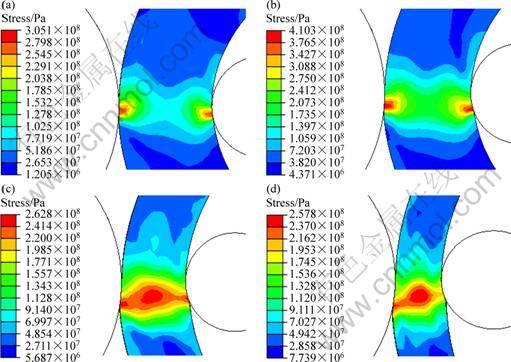
Fig. 4 Contours of Mises stress field in ring 3 at different time: (a) 0.67 s; (b) 1.67 s; (c) 9.67 s; (d) 16.67 s

Mises stress and stress components distributing a long the radial directions of three deformed rings in deformation zones are plotted in Fig. 5, where the horizontal axis x_t represents the distance between a point and the inside surface of a ring along the radial direction of the ring. From Fig. 5(a), the inside layer of ring 1 has a larger Mises stress than the outside and middle layers. The radial stress (S11)is compressive and its absolute value is much greater than the other stress components. The tangential stress (S22) and axial stress (S33) are compressive in surface layers (i.e., inside and outside layers) while are tensile in the middle layer. This is caused by nonuniform deformation, i.e., the surface layers are larger in deformation than the middle layer, which is constrained by the integrity of a ring, so surface layers exert additional tensile stress on the middle layer, while the latter imposes additional compressive stress on the former. The additional stress is superposed on the basic stress created by the external force，which gives rise to the stress state shown in Fig. 5(a). Furthermore, the absolute values of S11, S22 and S33 in surface layers are larger than those in the middle layer. The result is also observed numerically by SONG et al [7] from hot rolling of a small ring and UTSUNOMIYA et al [8] from cold rolling of a small ring. It can also be seen that three shear stress components (S12，S13 and S23) have less absolute values compared with normal stress components. To sum up, the surface layer of ring 1 is in the 3D compressive stress state, while the middle layer is in the 1D compressive and 2D tensile stress state, which implies that crack may form in the middle layer, particularly when hard wrought material is concerned. It is found from Fig. 5(b) that ring 2 is similar in stress distribution to ring 1. The differences between them are that it is the middle layer instead of the inside layer that has larger Mises stress, and S33 is all compressive along the radial direction for ring 2. Thus the middle layer of ring 2 is in the 2D compressive and 1D tensile stress state. Ring 3 also has similar stress distribution to ring 1, as shown in Fig. 5(c). The discrepancy between them is that the middle layer of ring 3 has larger Mises stress.

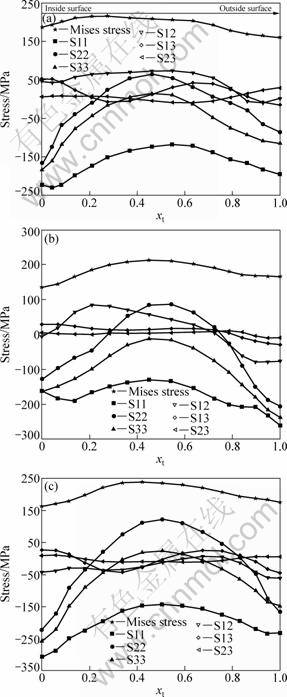
Fig. 5 Mises stress and stress components distributing along radial directions of deformed rings in deformation zones:    (a) Ring 1; (b) Ring 2; (c) Ring 3

4.2 Strain field

Figure 6 shows contours of equivalent plastic strain (PEEQ) field in ring 1 at different time (only the upper half of the ring is shown, the same as below). It is observed from Fig. 6(a) that PEEQ generates in the deformation zone first, with the surface of the outside layer (index A) having peak value and the middle layer (index C) having a minimum value. Then PEEQ propagates along the tangential direction of the ring (Fig. 6(b)) and finally deformation occurs in the whole ring (Figs. 6(c) and (d)). Meanwhile, PEEQ gradually increases and exhibits axisymmetrical distribution after the first revolution of the ring, as shown in Figs. 6(c)  and (d).

Contours of PEEQ fields in ring 2 and ring 3 at different time are illustrated in Fig. 7 and Fig. 8, respectively. Figure 7 indicates that ring 2 has similar PEEQ distribution to ring 1. This PEEQ distribution compares well with that of cold rolled small ring obtained numerically by UTSUNOMIYA et al [8] and that of hot rolled small ring obtained numerically by both XU et al [16] and LIM et al [17]. However, the simulation results for ring 3 are somewhat different: at the later stage, the peak PEEQ of ring 3 transfers from the outside surface to the inside surface (Figs. 8(c) and (d)), which is in agreement with the simulation results of hot rolling of a small ring obtained by SONG et al [7]. The difference between the three rings may depend strongly on the value of . According to Eq. (2), the value of  decreases in turn from ring 1 to ring 3, which indicates that the deformation in the outside layer decreases while that in the inside layer increases, and thus the peak PEEQ of ring 3 takes place in the inside layer instead of the outside layer during most of the forming stage with the exception of the early stage (Fig. 8(a)). The reason for the exception is that γ still has a relative larger value at the early stage.

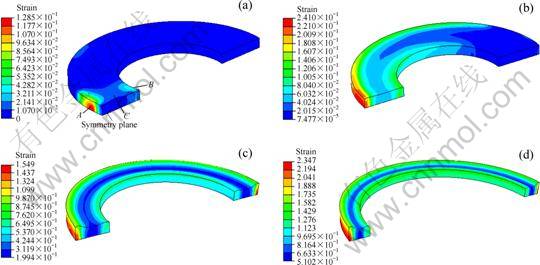
Fig. 6 Contours of PEEQ field in ring 1 at different time: (a) 0.67 s; (b) 1.67 s; (c) 9.67 s; (d) 16.67 s

Fig. 7 Contours of PEEQ field in ring 2 at different time: (a) 0.67 s; (b) 1.33 s; (c) 9.67 s; (d) 16.67 s

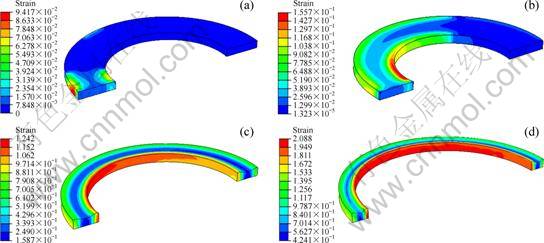
Fig. 8 Contours of PEEQ field in ring 3 at different time: (a) 0.67 s; (b) 1.33 s; (c) 9.67 s; (d) 16.67 s

Figure 9 shows the schematic diagram of locations of characteristic points. Figure 10 shows PEEQ evolution at characteristic points illustrated in Fig. 9. From Fig. 10, PEEQ of all the characteristic points increases like “ladder” with time. This is related to the revolution motion of a ring. That is, PEEQ increases when these points pass through the deformation zone, and maintains unchanged when they revolve out of the deformation zone. It can also be seen that for ring 1 and ring 2, the outside layer (P₃ and P₆) has larger PEEQ than the inside layer (P₁ and P₄), and the PEEQ in the middle layer (P₂ and P₅) is the minimum; for ring 3, the larger PEEQ appears in the inside layer instead of the outside layer.

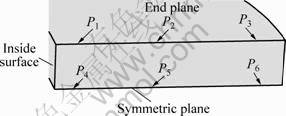
Fig. 9 Schematic diagram of locations of characteristic points on ring

PEEQ and strain components distributing along the radial direction of three deformed rings are plotted in Fig. 11. It is found from Fig. 11(a) that the outside layer of ring 1 has greater PEEQ than the inside and middle layers. The radial strain (P₁₁) is compressive and its absolute value generally is larger than the other components. The tangential strain (P₂₂) and axial strain (P₃₃) are tensile and the former is greater than the latter. In addition, the absolute values of P₁₁ and P₃₃ in the surface layers are larger than those in the middle layer, while that of P₂₂ decreases gradually from the inside layer to the outside layer. Moreover, the absolute values of shear strain P₁₂ and P₁₃ are greater than that of P₂₃ which fluctuates around zero, and all the shear strains exhibit alternate signs along the radial direction. To conclude, the whole ring is in 1D compressive and 2D tensile strain state. From Figs. 11(b) and (c), both ring 2 and ring 3 have similar strain distribution to ring 1, with the exception of the peak PEEQ of ring 3 in the inside layer.

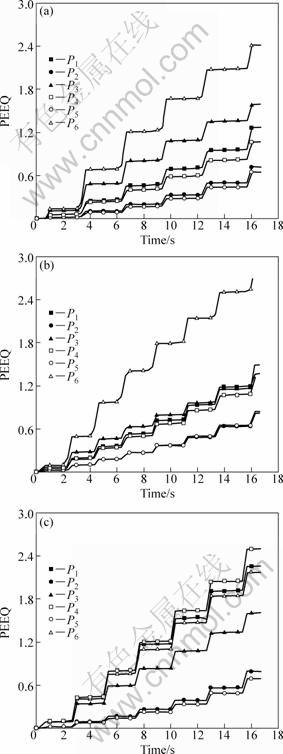
Fig. 10 PEEQ evolution at characteristic points: (a) Ring 1;   (b) Ring 2; (c) Ring 3

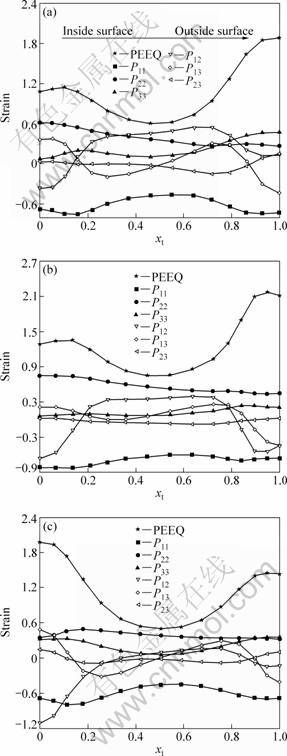
Fig. 11 PEEQ and strain components distributing along radial directions of deformed zones: (a) Ring 1; (b) Ring 2; (c) Ring 3

5 Conclusions

1) For all the rings, the peak Mises stress increases and then decreases, and the equivalent plastic strain field exhibits an axisymmetrical distribution after the first revolution of a ring.

2) For forming processes of different rings, as 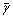 (the equivalent distribution ratio of feed amount per revolution of a process) decreases, the final peak Mises stress may transfer from the biting point at the driver roll side to that at the idle roll side, the final peak equivalent plastic strain may transfer from the outside surface to the inside surface, and the minimum equivalent plastic strain always exists in the middle layer; as  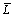(the equivalent deformation zone length of a process) increases, the final peak Mises stress may appear in the middle layer. The final positions of peak Mises stress and equivalent plastic strain are the combined effects of the above two aspects.

3) The absolute values of the stress and strain components along the radial direction of a ring are greater than those along the axial and tangential directions; in the deformation zone, the surface layer of a ring is in the 3D compressive stress state, while the middle layer is in the 1D compressive and 2D tensile stress state or 2D compressive and 1D tensile stress state; the whole ring is in the 1D compressive and 2D tensile strain state.

4) The middle layer of a ring is prone to crack formation, which is particularly true for hard wrought material such as titanium alloy.

References

[1] YANG He, SUN Zhi-chao, ZHAN Mei, GUO Liang-gang, LIU Yu-li, LI Hong-wei, LI Heng, WU Yue-jiang. Advances in control of unequal deformation by locally loading and theories related to precision plastic forming [J]. Journal of Plasticity Engineering, 2008, 15(2): 6-13. (in Chinese)

[2] GROCHE P, FRITSCHE D, TEKKAYA E A, ALWOOD J M. Incremental bulk metal forming [J]. Annals of the CIRP, 2007, 56(2): 635-656.

[3] SUN Mu-rong, HU Li-ping, NI Li-yong. Progress in FEM software technology for large forgings [J]. China Metalforming Equipment & Manufacturing Technology, 2004, (4): 83-86. (in Chinese)

[4] WANG Min, YANG He, SUN Zhi-chao, GUO Liang-gang. Dynamic explicit FE modeling of hot ring rolling process [J]. Transactions of Nonferrous Metals Society of China, 2006, 16(6): 1274-1280.

[5] HU Hong-jun, ZHANG Ding-fei, PAN Fu-sheng. Die structure optimization of equal channel angular extrusion for AZ31 magnesium alloy based on finite element method [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(2): 259-266.

[6] XU Si-guang, LIAN Jia-chuang, YAO Kai-yun, ZHAO Dong-hai, XU Da-cai. Experimental study on strain distribution in ring rolling [J]. Forging and Stamping Technology, 1991(1): 35-39. (in Chinese)

[7] SONG J L, DOWSONA A L, JACOBSA M H, BROOKS J, BEDEN I. Coupled thermo-mechanical finite-element modeling of hot ring rolling process [J]. J Mater Process Tech, 2002, 121: 332-340.

[8] UTSUNOMIYA H, SAITO Y, SHINODA T, TAKASU I. Elastic-plastic finite element analysis of cold ring rolling process[J]. J Mater Process Tech, 2002, 125-126: 613-618.

[9] WANG Z W, ZENG S Q, YANG X H, CHENG C. The key technology and realization of virtual ring rolling[J]. Journal of Materials Processing Technology, 2007, 182(1-3): 374-381.

[10] KIM K H, SUK H G, HUB M Y. Development of the profile ring rolling process for large slewing rings of alloy steels [J]. Journal of Materials Processing Technology, 2007, 187-188: 730-733.

[11] HUA Lin, HANG Xing-gao, ZHU Chun-dong. Theory and technology of ring rolling[J]. Beijing: Mechanical Industry Press, 2001. (in Chinese)

[12] YANG H, WANG M, GUO L G, SUN Z C. 3D coupled thermo-mechanical FE modeling of blank size effects on the uniformity of strain and temperature distributions during hot rolling of titanium alloy large ring[J]. Computational Materials Science, 2008, 44: 611-621.

[13] HU Z M, BROOKS J W, DEAN T A. The interfacial heat transfer coefficient in hot die forging of titanium alloy [J]. Journal of Mechanical Engineering C, 1998, 212(6): 485-496.

[14] LEE R S, LIN H C. Process design based on the deformation mechanism for the non-isothermal forging of Ti-6Al-4V alloy [J]. J Mater Process Tech, 1998, 79: 224-235.

[15] FU Zu-zhu. Non-ferrous metal plate manufacture [J]. Changsha: Central South University Press, 2009. (in Chinese)

[16] XU S G, WEINMAM K J, YANG D Y. Simulation of the hot ring rolling process by using a thermo-coupled three-dimensional rigid-viscoplastic finite element method [J]. J Manufact Sci Eng, 1997, 119: 542-549.

[17] LIM T, PILLINGER I, HARTLEY P. A finite-element simulation of profile ring rolling using a hybrid mesh model [J]. J Mater Process Tech, 1998, 80-81: 99-205.

钛合金大型环件热辗扩成形应力-应变场

演变规律的尺寸效应

王 敏^{1, 2}

1. 湖北汽车工业学院 材料工程系，十堰 442002；

2. 重庆大学 材料科学与工程学院，重庆 400044

摘  要：基于可靠的钛合金大型环件热辗扩成形过程热力耦合三维有限元模型，研究并对比了不同尺寸环件的应力应变场演变规律。结果表明：对于不同尺寸环件的成形过程，当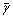（整个成形过程的当量每转进给量分配比）减小时，成形结束时的Mises应力峰值可能从环件的驱动辊侧咬入点转移至芯辊侧咬入点，而等效塑性应变峰值有从环件外表面向内表面转移的可能性；当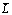（整个成形过程的当量变形区长度）增大时，成形结束时的Mises应力峰值可能出现在中间层。成形结束时Mises应力峰值和等效塑性应变峰值的位置是以上两方面综合作用的结果。在成形环件的变形区，环件表层金属处于三向压缩应力状态，中间层金属处于一向压缩、两向拉伸或者两向压缩、一向拉伸应力状态；整个环件处于一向压缩、两向拉伸应变状态。

关键词：钛合金；大型环件热辗扩；应力-应变；建模仿真；有限元

(Edited by YANG Hua)

Foundation item: Project (51005258) supported by the National Natural Science Foundation of China

Corresponding author: WANG Min; Tel: +86-719-8238783; E-mail: sprit418@mail.nwpu.edu.cn

DOI: 10.1016/S1003-6326(11)60904-7