高强钢绞线网加固RC梁抗剪性能及计算方法

黄华^{1, 2}，刘伯权¹，吴涛¹

(1. 长安大学 建筑工程学院，陕西 西安，710061；

2. 长安大学 旧桥检测与加固技术交通行业重点实验室，陕西 西安，710064)

摘要：对高强不锈钢绞线网-渗透性聚合物砂浆加固的9根矩形钢筋混凝土梁进行试验研究，并采用有限元程序对抗剪加固梁进行数值计算，分析混凝土强度、原梁配箍率、钢绞线用量、固定螺栓的数量和间距、加固方式、剪跨比、二次受力等因素对加固性能的影响。在试验研究和理论分析的基础上，提出抗剪加固承载力计算公式。研究结果表明：该加固工艺能够显著提高混凝土梁的抗剪承载力；多而密的固定螺栓对原梁抗剪承载力造成极大削弱；U形加固与环包加固对抗剪承载力提高程度有一定影响，且破坏模式和钢绞线的利用率有显著区别；持载程度高的梁加固承载力提高幅度低，但修复加固梁效果显著；随混凝土强度和配箍率提高，极限承载力提高。

关键词：高强钢绞线网；加固；抗剪性能；数值分析

中图分类号：TU375.102          文献标志码：A         文章编号：1672-7207(2011)08-2485-08

Shear performance and design methods of strengthened RC beams with high strength steel wire mesh

HUANG Hua^{1, 2}, LIU Bo-quan¹, WU Tao¹

(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;

2. Key Laboratory of Bridge Detection and Reinforcement Technology, Ministry of Communication,

Chang’an University, Xi’an 710064, China)

Abstract: Experiments were conducted to investigate the shear behavior of nine strengthened RC rectangular beams, and the finite element methods were used to analyze the shear performance of strengthened beams. The influence of concrete strength, stirrup ratio, quantity of stainless steel wire, bolts’ amount, bolts’ distance, strengthening mode and shear span ratio, secondary load on the shear performance were discussed. Based on experiments and theory analysis, the design formulae of shear capacity were proposed. The test results show that the rehabilitation greatly increases the beam’s shear load-carrying capacity. Too much and dense bolts badly weaken the shear behavior of beam itself. The influences of the strengthening manners on the load capacity are puny, and the beams’ failure modes and the utilization ratio of stainless steel wire are remarkably different. The increasing range of the beam’s load-carrying capacity is lower if its secondary load is bigger. But the rehabilitation effects of the failure beams are remarkable. With the increase of concrete strength and stirrup ratio, the strengthened beam’s ultimate bearing capacity increases.

Key words: high strength steel wire mesh; reinforcement; shear performance; numerical analysis

近年来，高强不锈钢绞线网-渗透性聚合物砂浆加固技术在国内外得到越来越广泛的使用，比较典型的有北京市方兴宾馆楼板加固工程、中国美术馆加固改造工程以及河北沧州东关大桥加固工程等。对该加固技术的研究主要集中在抗弯加固方面^[1-4]，而对抗剪加固方面所进行的研究较少，各种试验资料相对缺乏，已有研究^[5-6]考虑的影响因素不够全面，加固设计、施工规范尚不完善。在此，本文作者通过9根钢筋混凝土矩形梁的抗剪加固试验和12根钢筋混凝土矩形梁的抗剪加固数值计算，分析加固梁抗剪破坏机理，探讨混凝土强度、钢绞线用量、持载程度、加固方式、配箍率、螺栓的数量和间距、剪跨比等对加固性能的影响，提出相关加固设计计算公式。

1  抗剪加固试验

抗剪加固试验共制作9根钢筋混凝土矩形梁，尺寸及配筋如图1所示。混凝土强度为48.45 MPa；箍筋直径为6 mm，屈服强度为353.63 MPa，极限强度为524.88 MPa；纵筋直径为22 mm，屈服强度为452.63 MPa，极限强度为619.30 MPa；加固用高强钢绞线直径为3.2 mm，极限强度为1 606 MPa。试验梁加固方案如图2所示，编号及分类见表1。表1中：RCBS-1~5号构件为一次受力构件，加固前未加载；RCBS-6~8为二次受力构件，6号和7号分别加载至对比梁极限荷载的48%和58%时，进行持载加固，8号则加载至极限荷载后完全卸载，并进行修复加固。

加固构件剪力-挠度曲线见图3，主要试验结果见表2。由图3及表2可见，加固后各梁的特征荷载均得到了不同程度的提高，梁抗剪加固的效果非常显著；钢绞线固定用膨胀螺栓的数量对加固承载力有明显影响，螺栓过多、间距过小时会对原梁造成较大损伤；持载48%的加固梁与完整加固梁承载力相差不大，但持载程度58%的加固梁承载力提高幅度明显减小；2号环包加固梁承载力提高幅度明显比U形加固梁的提高幅度低；8号环包加固的修复梁屈服承载力提高幅度与U形加固梁的相当，但极限承载力提高幅度较低。

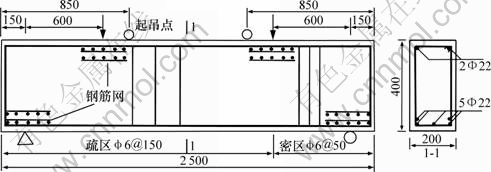
图1  加固梁截面尺寸及配筋(单位：mm)

Fig.1  Profile and reinforcement of cross section

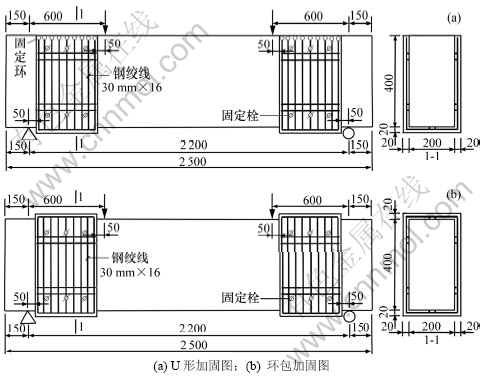
图2  加固示意图(单位：mm)

Fig.2  Strengthening design of specimens

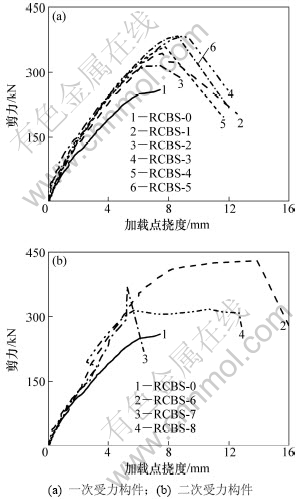
图3  剪力-挠度曲线

Fig.3  Shear capacity-deflection curves

表1  加固试件编号及分类

Table 1 　Number and sort of strengthened beams

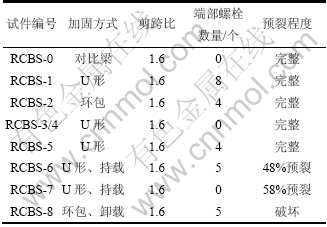
表2  主要试验结果

Table 2  Main test results

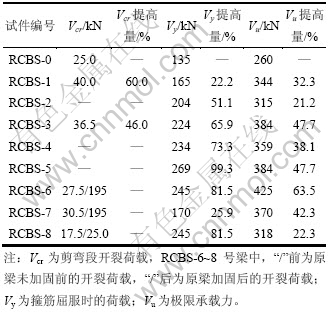
典型的破坏模式如图4所示，构件最终均发生加固层剥离破坏，在剥离的瞬间，荷载全部传递给压区混凝土，构件瞬间剪切破坏而丧失承载力。持载加固梁与完整加固梁相比，前者发生剥离破坏的突然性较后者的更大，脆性破坏更强烈；U形加固梁与环包加固梁相比，前者直接在梁顶产生层间裂缝而发展成剥离，后者沿顶部和底部砂浆层出现水平贯通裂缝，然后发展为剥离。

图4  加固梁破坏形态图

Fig.4  Failure mode of strengthened beam

2  抗剪加固数值分析

2.1  有限元试验验证

基于以上试验，利用有限元程序ANSYS，建立数值模型，分析混凝土强度、配筋率、钢绞线用量、加固方式、剪跨比等对抗剪性能的影响。混凝土采用Soild65单元和Willian-Warnke五参数破坏准则确定，单轴抗压应力-应变曲线采用Hongnestad模型确定；钢筋采用Link8单元和双线性随动强化模型(KINH) 确定，应力-应变曲线采用弹塑性强化模型确定；对于加固层的剥离，则通过文献[7]描述的黏结-滑移本构关系来考虑^[8-11]。

有限元计算与试验所得剪力-挠度对比曲线见图5。图中FEMS-48为有限元计算曲线，RCBS-3~5为试验曲线。其中，有限元计算的极限荷载与试验均值的差值为0.74%，挠度的差值为3.89%，表明有限元计算结论正确，可用于加固梁的参数分析。

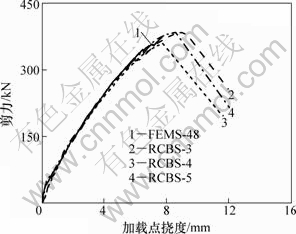
图5  剪力-挠度对比曲线

Fig.5  Shear capacity-deflection contrast curves

2.2  加固梁参数分析

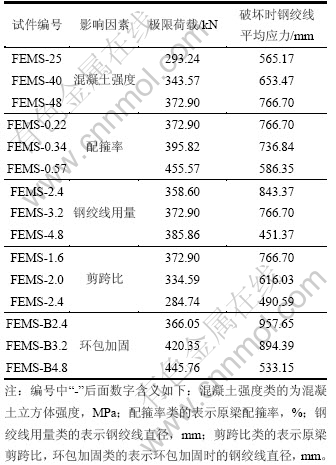
抗剪加固梁参数分析主要考虑以下几种因素：混凝土强度、配箍率、钢绞线用量、剪跨比和加固方式。计算结果见表4。由表4可见：混凝土强度和配箍率对抗剪加固梁受力性能有非常大的影响，随混凝土强度和配箍率提高，极限承载力提高，但钢绞线利用率前者提高而后者降低；无论是U形加固还是环包加固，随钢绞线用量的增加，构件极限承载力均提高，但后者提高幅度要远大于前者的提高幅度；随钢绞线用量增加，其利用率降低，但环包加固的钢绞线利用率较高；随剪跨比增大，主拉应力对破坏的贡献越来越大，抗剪承载力和钢绞线的利用率均逐步降低。

表4  抗剪加固梁数值计算结果

Table 4  Numerical analysis results of shear strengthened beams

3  抗剪加固计算公式

3.1  抗剪加固理论分析

加固后的钢筋混凝土梁抗剪承载力主要成分由下列几部分组成：斜裂缝上端、靠梁顶部未开裂混凝土的抗剪力V_c，沿斜裂缝的混凝土骨料咬合作用V_i，纵筋的横向(销栓)力V_d，箍筋和弯起钢筋的抗剪力V_sv、V_b，加固聚合物砂浆的抗剪力V_m，加固高强钢绞线的抗剪力V_sw等，加固梁斜截面抗变力作用示意图如图6所示。这些抗剪成分的作用和相对比例，在构件的不同受力阶段随裂缝的形成和发展而不断地变化。构件极限状态的抗剪承载力为这几部分的总和：

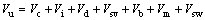      (1)

加固梁的主要抗剪成分所承担的剪力比例，取决于混凝土的强度、腹筋、纵筋、弯起钢筋、聚合物砂浆、高强钢绞线的数量和布置方式等因素，在各受力阶段不断地发生变化。而且荷载的位置(剪跨比)对梁的破坏形态也有很大影响。

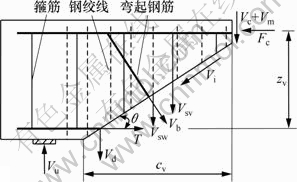
图6  加固梁斜截面抗剪作用

Fig.6  Shear resistance of oblique section of strengthened beam

3.2  加固层抗剪能力计算

高强钢绞线网-聚合物砂浆抗剪加固承载力设计主要需解决加固部分的抗剪承载力。众多对粘贴FRP抗剪加固的研究^[12-14]也是在原梁抗剪承载力基础上，考虑FRP材料对抗剪承载力的贡献。令高强钢绞线  网-聚合物砂浆加固层对抗剪承载力的贡献为：

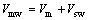               (2)

式中：V_mw为加固层的抗剪承载力；V_m为加固聚合物砂浆的抗剪承载力；V_sw为加固高强钢绞线的抗剪承载力，分别由式(3)和(4)计算。

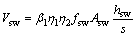            (3)

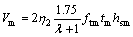             (4)

式中：β₁为加固方式影响系数；η₂为加固体与本体梁之间共同工作系数，U形加固取值为0.9，环包加固在此基础上提高0.1；η₁为钢绞线应力发挥综合系数，由于抗剪加固基本上发生剥离破坏，故其取值与抗弯加固^[15]有所差别。

对加固方式影响系数β₁，根据表4中抗剪加固破坏时高强钢绞线的平均应力，环包加固时，β₁=1.15；U形加固时，β₁=1.0。

对钢绞线应力发挥综合系数η₁，由表4中数据分析可见，其与混凝土立方体抗压强度、钢绞线直径、剪跨比均有联系，而原梁配箍率的影响不大，故此处不考虑其影响。η₁可由下式表示：

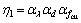               (5)

式中：α_fcu为混凝土立方体抗压强度影响系数；α_d为钢绞线直径影响系数；α_λ为剪跨比影响系数，这些影响因素与应力的关系见图7。图中拟合曲线分别为：

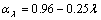 (相关系数为0.999)

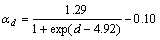 (相关系数为1)

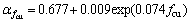 (相关系数为1)

从而可得钢绞线应力发挥综合系数η₁的公式为：

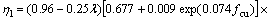
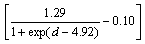
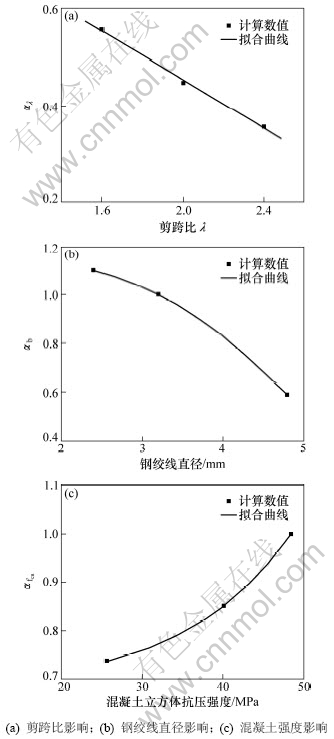
图7  钢绞线应力发挥综合系数影响因素关系

Fig.7  Relationship between stress of stainless steel wire and its influencing factors

聚合物砂浆及高强钢绞线的有效高度h_sm和h_sw取值如图8所示。其中：h_z为加固层顶面至梁顶面的距离；d_z为钢绞线顶端至砂浆层顶面距离；h为梁高；h_f^’为翼缘高度；h₀为钢筋有效高度；t_m为加固层厚度。

对U形加固，由图5(a)可得如下关系：

，

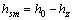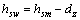
当翼缘高度为0时，T形梁转化为矩形梁，则有h_sm=h₀；当d_z=0时，有h_sm=h_sw=h₀。

对环包加固，由图7(b)可得如下关系：h_sm= h₀+t_m；对于h_sw，与h_sm略有差异，可近似认为h_sw= h_sm。

3.3  加固构件抗剪承载力计算

在式(2)基础上根据现行规范，建立加固构件抗剪承载力计算公式。

对《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62-2004(以下简称《公路桥规》)而言，受弯构件斜截面抗剪承载力计算如下：

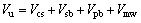          (6)

式中：V_u为构件极限抗剪承载力；V_cs为斜截面内混凝土和箍筋共同的抗剪承载力；V_sb为与斜截面相交的普通弯起钢筋抗剪承载力；V_pb为与斜截面相交的预应力弯起钢筋抗剪承载力；具体计算参见《公路桥规》。

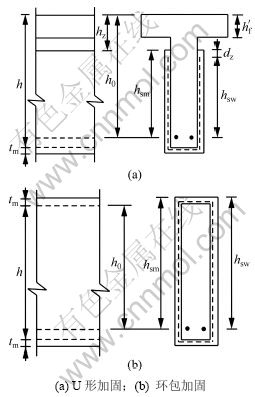
图8  加固层有效高度取值

Fig.8  Value of effective highness of reinforced layer

对于《混凝土结构设计规范》GB 50010-2010(以下简称《混凝土规范》)，受弯构件斜截面抗剪承载力计算如下：

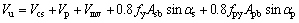(7)

式中：V_p为预加力所提高的构件抗剪承载力；0.8f_yA_sbsinα_s为与斜截面相交的普通弯起钢筋抗剪承载力；0.8f_pyA_pbsinα_p与斜截面相交的预应力弯起钢筋抗剪承载力。具体计算参见《混凝土规范》。

式(2)，(6)和(7)计算值与试验值对比见表5。对V_mw，计算值与试验值和数值试验值比值的均值为0.973，方差为0.108，离散系数为0.111，由此可见：公式计算加固层提供的抗剪承载力是符合实际的，与试验结果较符合，公式计算值偏于安全。式(6)按《公路桥规》计算值与试验值和数值计算值比值的均值为0.719，方差为0.046，离散系数为0.064，由此可见：公式计算加固梁抗剪承载力是符合桥梁实际的，公式计算值偏于安全，试验值是计算值的1.39倍，已具备较高的安全储备。如需达到更高的安全储备，可将共同工作系数η₂取0.7或更低的值。式(7)按《混凝土规范》计算值与试验值和数值计算值比值的均值为0.928，方差为0.039，离散系数为0.042，表明计算值与试验值较符合，公式计算值偏于安全，已具备一定的安全储备。

表5中试验数据涵盖了混凝土强度、原梁配箍率、加固钢绞线用量、持载程度、剪跨比、加固方式等参数对加固的影响。式(6)和(7)具有较好的适应性，可用于各自结构的抗剪加固承载力设计。

此外，对原梁抗剪承载力损伤较为严重的梁抗剪加固承载力计算时，须对原梁的承载力进行折减，此处引入原梁损伤系数η_d，式(6)和(7)变为式(8)和(9)。

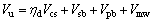          (8)

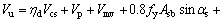
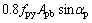              (9)

对于锚固高强钢绞线网的螺栓过多造成的损伤，损伤系数η_d取0.8；对于原梁损伤很大、箍筋已屈服的修复构件如RCBS-8，损伤系数η_d取0.55或者更低的值；没有损伤或损伤很小的构件，损伤系数η_d取1.0。损伤梁加固抗剪承载力试验值与计算值对比见表6。由表6可见：计算结果有较大的安全储备，公式可用于工程设计。

表5  抗剪加固梁计算值与试验值对比

Table 5  Comparison between calculation values and experimental results of shear strengthened beams

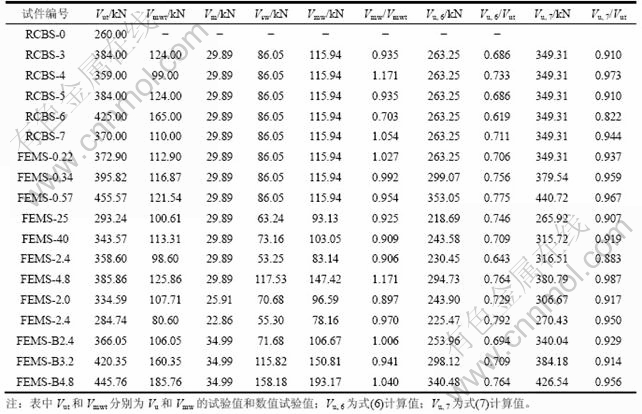
表6  损伤梁抗剪加固计算值与试验值对比

Table 6  Comparison between calculation values and experimental results of shear strengthened damaged beams

4  结论

(1) 高强钢绞线网-聚合物砂浆抗剪加固效果显著，梁抗剪承载能力得到了大幅度提高，裂缝发展得到了有效延迟。

(2) 钢绞线网固定用螺栓数量对抗剪加固承载力有显著影响，螺栓间距过密时，对梁斜截面造成较大损伤，承载力提高幅度比其他梁的提高幅度低1/3~1/2。

(3) 受多个方向的应力复合作用，加固层最终发生剥离，混凝土压碎而破坏。U形加固梁直接在梁顶产生层间裂缝而发展为剥离；环包加固梁沿顶部和底部砂浆层出现水平贯通裂缝，然后发展为剥离；后者延迟了剥离破坏的发生，对改善抗剪加固性能有很大作用。

(4) 持载加固与完整加固梁相比，破坏过程相似，但前者脆性破坏更加明显；且持载程度对抗剪承载力有显著影响，持载程度高，加固承载力提高幅度低，但修复加固梁效果显著。

(5) 混凝土强度和配箍率对抗剪加固梁受力性能有非常大的影响，随混凝土强度和配箍率提高，极限承载力提高，但前者的钢绞线利用率提高而后者    降低。

(6) 无论是U形加固还是环包加固，随钢绞线用量的增加，构件极限承载力提高，而钢绞线利用率降低，且后者承载力提高幅度及钢绞线利用率均要比前者的大。

(7) 在试验研究和理论分析的基础上，提出抗剪加固承载力计算公式，可为工程实际提供参考。

参考文献：

[1] Ong K C G, Paramsivam P, Lim C T E. Flexural strengthening of reinforced concrete beams using ferrocement laminates[J]. Journal of Ferrocement, 1992, 22(4): 331-342.

[2] Paramsivam P, Ong K C G, Lim C T E. Ferrocement laminates for strengthening RC T-beams[J]. Cement & Concrete Composites, 1994, 16(2): 143-152.

[3] 聂建国, 王寒冰, 张天申, 等. 高强不锈钢绞线网-渗透性聚合砂浆抗弯加固的试验研究[J]. 建筑结构学报, 2005, 26(2): 1-9.
NIE Jian-guo, WANG Han-bing, ZHANG Tian-shen, et al. Experimental study on flexural behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures, 2005, 26(2): 1-9.

[4] SHANG Shou-ping, ZENG Ling-hong, PENG Hui. Flexural strengthen of reinforced concrete beam with ferrocement[C]// Proceedings of the 28th Conference on All World in Concrete and Structures. Singapore, 2003: 28-29.

[5] 黄华, 刘伯权, 刘卫铎. 高强钢绞线网-聚合物砂浆抗剪加固梁二次受力试验研究[J]. 工业建筑, 2009, 39(2): 99-102.
HUANG Hua, LIU Bo-quan, LIU Wei-duo. Experimental study of shear behavior of RC beams strengthened with stainless steel wire mesh and polymer mortar under secondary load[J]. Industrial Construction, 2009, 39(2): 99-102.

[6] 聂建国, 蔡奇, 张天申, 等. 高强不锈钢绞线网－渗透性聚合砂浆抗剪加固的试验研究[J]. 建筑结构学报, 2005, 26(2): 10-17.
NIE Jian-guo, CAI Qi, ZHANG Tian-shen, et al. Experimental study on shear behavior of RC beams strengthened with stainless steel wire mesh and permeability polymer mortar[J]. Journal of Building Structures, 2005, 26(2): 1-9.

[7] 黄华. 高强钢绞线网-聚合物砂浆加固钢筋混凝土梁式桥试验研究与机理分析[D]. 西安: 长安大学建筑工程学院, 2008: 63-68.
HUANG Hua. Experimental study and theoretical analysis on strengthening RC girder bridge with steel wire mesh and polymer mortar[D]. Xi’an: Chang’an University. School of Civil Engineering,2008: 63-68.

[8] Padmarajaiah S K, Ramaswamy A. A finite element assessment of flexural strength of prestressed concrete beams with fiber reinforcement[J]. Cement & Concrete Composites, 2002, 24(2): 229-241.

[9] 杨勇, 郭子雄, 聂建国, 等. 型钢混凝土结构ANSYS数值模拟技术研究[J]. 工程力学, 2006, 27(4): 79-85.
YANG Yong, GUO Zi-xiong, NIE Jian-guo, et al. Study on numerical simulation technology of steel reinforced concrete structures using ASNYS[J]. Engineering Mechanics, 2006, 27(4): 79-85.

[10] 杨勇, 赵鸿铁, 薛建阳, 等. 型钢混凝土基准粘结滑移本构关系试验研究[J]. 西安建筑科技大学学报: 自然科学版, 2005, 37(4): 445-449.
YANG Yong, ZHAO Hong-tie, XUE Jian-yang, et al. Experiment study on basic bond-slip constitutive relationship models between shaped-steel and concrete in SRC structures[J]. Journal of Xi’an University of Architecture & Technology: Natural Science Edition, 2005, 37(4): 445-449.

[11] 江见鲸, 陆新征, 叶列平. 钢筋混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005: 44-176.
JIANG Jian-jing, LU Xin-zheng, YE Lie-ping. Finite element analysis of concrete structures[M]. Beijing: Tsinghua University Press, 2005: 44-176.

[12] Arduini M. Parametric study of beams with externally bonded FRP reinforcement[J]. ACI Structure Journal, 1997, 94(5): 465-482.

[13] Chen J F, Teng J G. Shear capacity of FRP strengthened RC beams: fiber reinforced polymer rupture[J]. Journal of Structural Engineering, 2003, 129(5): 615-625.

[14] Chen J F, Teng J G. Shear capacity of FRP strengthened RC beams: FRP debonding[J]. Construction and Building Materials, 2003, 17(1): 27-41.

[15] 黄华, 刘伯权, 邢国华, 等. 高强不锈钢绞线网-渗透性聚合砂浆加固的T型梁桥试验[J]. 中国公路学报, 2007, 20(4): 83-90.
HUANG Hua, LIU Bo-quan, XING Guo-hua, et al. Experiment on RC T-type beam bridge strengthened with high strength stainless steel wire mesh and permeability polymer mortar[J]. China Journal of Highway and Transport, 2007, 20(4): 83-90.

(编辑 赵俊)

收稿日期：2010-09-25；修回日期：2010-12-20

基金项目：高等学校博士点基金资助项目(20090205120008)；中央高校科研专项基金资助项目(CHD2009JC160)；长安大学基础研究专项基金资助项目(2009)

通信作者：黄华(1979-)，男，江苏常州人，博士，讲师，从事结构工程抗震及加固改造研究；电话：029-82337279；E-mail：huanghua23247@163.com