DOI: 10.11817/j.issn.1672-7207.2017.04.018

基于精确再生码的秘密共享方案

宋海龙^{1, 2}，王伟平¹

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；

2. 吉首大学 信息科学与工程学院，湖南 吉首，416000)

摘要：为解决云存储系统中数据安全性问题，利用精确再生码构造一种新的(t，n)门限秘密共享方案。方案由子秘密的分发、原始秘密的恢复和子秘密丢失者的数据重建共3种算法组成。子秘密的分发就是将原始秘密先进行分块，再进行纠删编码，最后按一定的规则将编码后的数据块分发给n个分享者。选取t个分享者提供的数据块，按纠删码的译码算法恢复原始秘密。选取t个以上分享者的数据块，按精确再生码的译码算法重建出子秘密丢失者的数据。研究结果表明：访方案是一种信息论安全的门限体制，与传统的基于Lagrange多项式插值算法的秘密共享方案相比，具有运算复杂性低、节点存储量小、丢失子秘密易再生等优点。

关键词：再生码；纠删码；网络编码；秘密共享；云存储；分布式存储

中图分类号：TP309             文献标志码：A         文章编号：1672-7207(2017)04-0984-06

Secret sharing scheme based on exact regenerating codes

SONG Hailong^{1, 2}, WANG Weiping¹

(1. School of Information Science and Engineering, Central South University, Changsha 410083,China;

2. School of Information Science and Engineering, Jishou University, Jishou 416000, China)

Abstract: In order to solve data security issues in cloud storage system, a new (t, n) threshold secret sharing scheme was constructed based on exact regenerating codes. The scheme was composed of three algorithms which were distribution of share secret, recovery of the original secret and data reconstruction of lost share secrets. Distribution of share secret means that original secret is firstly split into some pieces, then is erasured codes, and finally is distributed to n partners. Choosing data blocks provided by t partners, the original secret can be recovered through some decoding algorithms of erasure coding. Choosing more than t data blocks,the lost data of partner who losts his data can be reconstructed following decoding algorithm of exact regenerating codes. The results show that the scheme is an information theoretical secure threshold system. Compared with the traditional secret sharing scheme based on Lagrange polynomial interpolation algorithm, the scheme has the advantages of lower computation complexity, less nodes storage and easier regeneration of lost share secrets.

Key words: regenerating codes; erasure coding; network coding; secret sharing; cloud storage; distributed storage

秘密共享就是参与者共同享有秘密，单独1人不能得到秘密，只有达到一定门限值的人员共同提供自己的秘密份额，才可以得到完整秘密。利用秘密共享管理秘密，可以防止权力过度集中以致于被滥用。秘密共享也被应用于数据的加密存储或提供冗余保护等领域^[1-4]。自SHAMIR等^[5-6]提出秘密共享概念以来，人们已对其进行了广泛研究^[7-9]。但随着数据量增大，运行效率明显下降。近年来，人们发现利用最大距离可分码即MDS(the maximum distance separable)码^[10]可构建具有节点修复功能的分布式存储系统。按照该算法，将大小为M的数据文件分割编码为n个分片分别进行保存，每个分片大小为M/t，只要获得了其中任意t个分片，即可利用译码算法重建原始数据文件。然而，利用MDS码要先重建原始数据，再重新编码生成失效节点的数据。为解决此问题，DIMAKIS等^[11]根据网络编码(network coding)^[12]的思想提出了再生码(regenerating codes)的概念。利用再生码不但可以重建原始数据文件，而且可以直接或者间接重建失效节点的数据。若原始数据文件是个秘密，则利用再生码就可以构造秘密共享方案。本文介绍秘密共享中的门限方案和再生码的相关背景知识，给出基于精确再生码的秘密共享方案的描述，通过实例给出算法的实现过程，并分析方案的性能。

1  基本概念

1个秘密共享方案一般是由秘密空间K、秘密份额空间S、秘密分发者D、秘密享有者U={u₁，u₂，…，u_n}、访问结构Γ、秘密分发算法和秘密重构算法等构成。Γ为U的子集的集合，即Γ∈2^U。若Γ中的子集是能够计算出秘密k∈K的参与者的子集，则称Γ为访问结构。作为访问结构的特殊情况，Γ={A|A∈U, |A|≥t}称为门限访问结构，t称为门限值。门限访问结构是实现秘密共享的一种比较简单的方案。

1.1  (t，n)门限秘密共享方案

定义1  秘密K以某种方式被分割编码成n份秘密份额(或称为子秘密)并分别发放给n个参与者。n个参与者的集合记为U。若满足下列条件：A是U的授权子集当且仅当|A|≥t；而当A∈U且|A|＜t时，A得不到关于秘密K的任何信息，则称{U，K，A}构成1个(t，n)门限秘密共享方案，t称为门限值。

SHAMIR等^[5]利用Lagrange多项式插值算法给出了一种(t，n)门限秘密共享方案的实现方法。假设K为原始秘密，秘密分发者随机选择1个大素数p，要求p＞n，且p＞K，并构造1个次数为t-1的任意多项式：q(x)=(a_tx^t+a_t-1x^t-1+…+K)modp(其中，a_i为有限域GF(p)中随机选择的系数，它们是秘密的，在分发完共享秘密份额之后就丢弃，素数p须公开)。各个共享秘密份额通过计算该多项式在各个不同点上的值得到k_i=q(x_i)(其中：i=1，…，n；x_i为每个参与者的惟一标识号)。

只要能获得t个共享秘密份额，便可以利用Lagrange插值公式得出 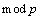，再令x=0即可得原始秘密K=q(0)modp。

上述算法在秘密的分发和恢复过程中要多次用到大整数模幂、模乘运算，运算量大，占用内存空间大，而这在有些环境下(如无线传感器网络、ad hoc网络等，其节点运算和存储能力有限)是无法接受的。随着研究深入，一些方案如基于同余理论的Asmuth-Bloom方案^[13]、基于矩阵乘法的Karnin-Greene-Hellman方案^[14]等被提出，这些方案并没有降低运算复杂度。

1.2  再生码

分布式存储系统的容错策略通常分为基于复制的容错技术和基于纠删码的容错技术共2种^[15]。基于纠删码的容错技术则对多个数据块及其冗余信息进行融合编码，可有效减小存储空间的开销, 但需要一些计算开销。以计算换空间的再生码能有效降低数据修复时的通信开销。下面通过例子说明再生码的原理。

例1  将1个大小为M的文件平均分割成A₁，A₂，B₁和B₂，按图1所示保存到4个节点中(其中“+”表示异或运算)，这就可以构成1个(4，2)再生码。再生码的编码规则比较简单，就是将原始数据分割(本例中分成4块)，确保每个节点中能存储2块，节点1和节点2是存储的原始数据，而节点3和节点4存储的是原始数据块经过异或后的数据，也就是编码后的数据块。

若节点1失效，则可以利用其他3个节点的数据B₂，A₂+B₂和A₁+A₂+B₂进行修复，所以，总的数据通信量为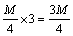。而若采用普通的MDS码，则数据通信量为。可见，采用再生码能节省0.25M的通信量。另一方面，若节点4失效(如图2所示)，则可利用其他3个节点的数据A₁，B₁+B₂和A₂+B₂进行修复，但在节点2处要先将本地的数据块进行异或运算得到B₁+B₂，也就是说，要求节点有一定的网络编码能力。此外，在修复过程中，连接的帮助节点数可以超过k=2，这也与纯粹的(4,2)-MDS码不同。

根据文献[11]的相关论述给出再生码的形式化定义。

定义2  给定1个大小为M的文件，将其进行某种编码后存储到n个节点，每个节点都存储大小为α的数据块。当某个节点失效时，置换节点能从剩余的n-1个节点中连接任意d个节点(t≤d≤n-1)，从每个节点下载大小为β≤α的数据，并通过某种译码算法恢复出失效节点的数据，则称这一模型构成1个参数集为(n，t，d，α，β，γ)的再生码(其中，γ=dβ为用于修复的整个数据下载量，称为修复带宽；d为修复度数；阈值t为能够恢复数据所需要的最小度数)。

图1  失效节点1的修复

Fig. 1  Repairing of failed node 1

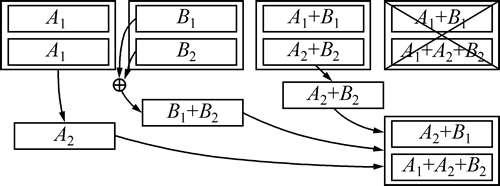
图2  失效节点4的修复

Fig. 2  Repairing of failed node 4

根据再生码的定义可知：只要能够恢复失效节点的数据，便可恢复整个原始数据。利用这一思想就可以构造秘密共享方案。

2  基于精确再生码的秘密共享方案

整个方案分为3个算法，即子秘密的分发、原始秘密的恢复以及失效节点的数据再生。

2.1  子秘密的分发

首先，将大小为M的原始秘密K平均分成f块(这里要求f≤n)，使每个数据块大小为t(若最后1块小于t就以0补齐)，即有M=ft，并记为K=(K⁽¹⁾，K⁽²⁾，…，K^(f))。利用某种(n，t)-MDS码编码算法将每个独立的长度为t的数据块K⁽ⁱ⁾编码成长度为n的向量x⁽ⁱ⁾，即

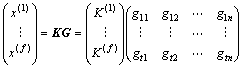    (1)

其中：G为t×n阶的MDS码生成矩阵，是可以公开的，而且要求G的任何一个子方阵都必须是可逆的。此外，还需要计算1个向量和。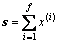

其次，给每个秘密分享者分配惟一的序列号u_i作为其识别号。将长度都为n的向量x⁽¹⁾，…，x^(f)和s按其分量循环分别分发到n个分享者手中。对于第j∈[1，n]个分享者，它得到的秘密份额为(x_j⁽¹⁾，x_j⊕1⁽²⁾，…，x_j⊕(f-1)^(f)， s_j⊕f)(其中，“⊕”表示模n加法)。每个秘密分享者存储的秘密份额如表1所示。

表1  各分享者存储的子秘密

Table 1  Share secrets stored in every partner

2.2  原始秘密的恢复

只要有t个分享者提供其子秘密便可恢复出原始秘密。以x⁽¹⁾为例，它的分量被分别分发给n个分享者，所以，只要有t个秘密份额，就可以根据MDS码的译码算法，求出原始秘密块K⁽¹⁾。若x₁⁽¹⁾，x₂⁽¹⁾，…，x_t⁽¹⁾已知，则据式(1)有，从而有。

由于生成矩阵G是公开的，且它的任何1个子方阵都是可逆的，故有

 (2)

这样就恢复了K⁽¹⁾这个数据块。同理，其他数据块K⁽²⁾，…，K^(f)也可以类似地被重建出来，这样就得到整个原始秘密K=(K⁽¹⁾，K⁽²⁾，…，K^(f))。

2.3  秘密丢失者的数据重建

若某一分享者的子秘密丢失，则不需要由秘密分发者重新进行秘密分发，只要有足够的分享者提供子秘密，便可重建出丢失的子秘密。与秘密恢复不同的是：必要时，秘密丢失者可以从多于t个分享者那里下载数据再生自己的秘密，而总的下载量小于原始秘密的下载量，从而可以节约带宽。

以分享者u₁的子秘密(x₁⁽¹⁾，x₂⁽²⁾，…，x_f^(f)，s_f⊕1)的重建为例。首先进行s_f⊕1重建。根据2.1中的定义， s_f⊕1=x_1⊕f⁽¹⁾+ x_1⊕f ⁽²⁾+…+ x_1⊕f ^(f)，因此，只要到秘密分享者u_f⊕1，u_f，…，u₂那里下载相应数据块再相加即可。其次进行数据块x₁⁽¹⁾的重建。这只要到相应节点下载s₁，x₁⁽²⁾，…，x₁^(f)，便有x₁⁽¹⁾=s₁+ x₁⁽²⁾+…+ x₁^(f)。同理，x₂⁽²⁾，…，x_f^(f)等都可以被重建出来。

以上算法称为基于(n，t，f)再生码的秘密共享方案，它是一种基于精确再生码算法的方案，可以精确恢复出丢失的秘密份额。

2.4  算法复杂度分析

子秘密的编码分发和秘密丢失者的数据重建只需进行矩阵的乘法运算，运算量不是很大。原始秘密的修复算法复杂度主要取决于生成矩阵G的求逆运算，而矩阵的求逆运算代价较高。根据再生码的编码要求，G的任何1个子方阵都必须可逆(否则可能无法恢复秘密)，若G的元素是在有限域GF(2^N)中随机选取，这种矩阵可逆的概率可达99.6%^[16]，所以，理论上可以用来作为再生码的编码矩阵。然而，对于这种一般矩阵，其逆矩阵的计算复杂度还是相当高。为提高效率，在算法的实现中可以采用范德蒙型矩阵作为生成矩阵。FINCK等^[17]利用基本对称函数乘积表算法得到了范德蒙矩阵求逆的固有复杂度为O(nlg²n)。SHAMIR^[5]方案的秘密恢复算法的时间复杂度为O(n²)，所以，本文方案在理论上效率更高。

3  算法的实现

在算法的具体实现中，可将源数据的最小符号看作是有限域GF(2^N)中的元素。由于目前计算机是以8 bit(即1个字节)为信息存储的最小单位，这里不妨取N=8。有限域中元素的加法就是异或运算，乘法运算则需要用到本原多项式。将有限域元素的二进制表示式看作降幂多项式的系数，2个元素相乘就相当于多项式相乘，再对本原多项式求模，所得结果再转化为向量。不妨取本原多项式m(x)=x⁸+x⁴+x³+x²+1作为模多项式，取任何其他8次本原多项式也都可以，对方案的实现无实质性影响。下面举例说明算法的具体实现。

例2  为了简便，不妨假设原始秘密K是4字节长的，其16进制ASCII码表示为K=(3a，5f，b9，e7)，以下利用基于(4，2，2)再生码的秘密共享算法进行处理。因为在进行MDS编码时需要1个2×4的生成矩阵G，这里不妨采用范德蒙矩阵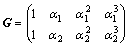，，其中，α_i都是有限域GF(2^N)中的非零元素，且要求α₁≠α₂，如取α₁=45，α₂=2c。范德蒙矩阵的特点是它的任何1个子方阵都是可逆的。

1) 子秘密的分发。首先对K=(K₁⁽¹⁾, K₂⁽¹⁾, K₁⁽²⁾, K₂⁽²⁾)进行MDS码编码，得

     (3)

将以上得到的数据再按顺序进行组合并发放到4个共享者，它们分别得到的子秘密数据如表2所示。

表2  分享者存储的子秘密

Table 2  Share secrets stored in every partner

2) 原始秘密的恢复。只要获得任意2个共享者的子秘密便可恢复原始秘密。例如，若获得u₁和 u₂的数据，则根据方程(1)可得

        (4)

由范德蒙矩阵的性质易知，作为G的子矩阵是可逆的，从而可得

    (5)

同理，可以根据x₂⁽²⁾和x₃⁽²⁾得(K₁⁽²⁾ K₂⁽²⁾)=(b9 e7)，这样就得到了整个原始秘密K=(K₁⁽¹⁾，K₂⁽¹⁾，K₁⁽²⁾，K₂⁽²⁾)=(3a，5f，b9，e7)。

3) 秘密丢失者的数据重建。假如u₁的秘密份额丢失，则可以到其他分享者下载相关数据块进行重建。x₁⁽¹⁾可以通过从u₃下载x₁⁽¹⁾+ x₁⁽²⁾以及从u₄下载x₁⁽²⁾，然后进行运算x₁⁽¹⁾+ x₁⁽²⁾+ x₁⁽²⁾= x₁⁽¹⁾得到；同理，易得x₂⁽²⁾。x₃⁽¹⁾+ x₃⁽²⁾可以通过从u₂下载x₃⁽²⁾和从u₃下载x₃⁽¹⁾再相加得到。

在具体实现中，若处理的文件较大，则可以对文件先进行条带化，使之变成一些大小相同的分块，再对每个分块分别使用本方案进行处理。此外，有限域的选取也可以根据硬件设备机器字的位数合理选取，一般选取较大的有限域可以提高效率。

4  实验与分析

为验证本文方案的可行性，将其与SHAMIR^[5]基于Lagrange多项式插值的门限方案进行对比。实验平台为Intel(R) Core2 Duo 2.20GHz CPU，2GB RAM，Windows XP PC机，Matlab R2014a编译环境。

4.1  效率对比

由于子秘密分发算法都只涉及有限域中矩阵的加法和乘法，对运行时间影响不大，所以，只对比2种方案的秘密恢复算法的效率。

实验：对1个大小为1 920字节的文件、门限值t和分享者数目n变化时2种方案的秘密恢复效率进行对比。

实验中2种方案的运算都是在有限域GF(2¹⁶)上进行的，即每次对2字节的数据块进行操作，在实际应用中可以根据硬件设备情况选择更大的有限域，效率会更高。每一组测试都独立运行20次，取其运行时间的平均值。当分享者数目和门限值变化时，实验结果如图3所示。

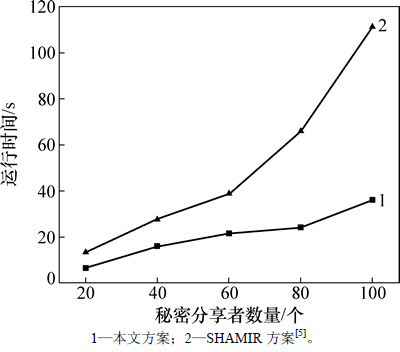
图3  运行时间随门限值及分享者数目的变化情况

Fig. 3  Change of running time with threshold and number of partners

从图3可以看出：在进行秘密恢复时，随着门限值及分享者数目增加，SHAMIR方案^[5]所需时间迅速增大，本文方案所需时间也较快增大。这是因为随着门限值及分享者数目的变大，编解码用到的生成矩阵G的规模也相应变大，在进行秘密恢复时用到的矩阵求逆运算非常耗时。但从实验结果看，本文方案所需时间增长速度比SHAMIR方案^[5]的要少，说明本文方案仍有一定优势。

4.2  安全性分析

再生码是在MDS纠删码^[18]基础上继续进行一定的线性变换而得到的，它仍然满足MDS纠删码的特性，因而可以看作是一种特殊的MDS码，PIEPRZYK等^[19]指出MDS码可以用来构造理想的门限体制。对于本文构造的算法，在此以定理的形式给出其安全性。

定理1  本文构造的基于(n，t，f)再生码的秘密共享算法，它是1个安全的(t，n)门限秘密共享体制。

证明：一方面，只要有t个分享者提供子秘密，就可以恢复出原始秘密K；另一方面，可证明当秘密份额少于t份时，就不能恢复出原始秘密。事实上，通过方程(1)可以看到，由于K⁽¹⁾ ，…，K^(f)是相互独立的，因而其线性变换x₁⁽¹⁾，…，x_f^(f)也是相互独立的。按照给出的再生码算法，每个分享者持有的子秘密来自于x₁⁽¹⁾ ，…，x_f^(f)以及s的不同分量，因而，其每个数据块之间也是相互独立的。这样，要想恢复某个数据块如x₁⁽¹⁾，就只能根据各个分享者提供的x₁⁽¹⁾相关分量来进行运算，这就归结到MDS码的译码问题上。在数据块少于k个情况下，这就相当于解1个方程数少于k的k元一次线性方程组，它具有无穷多个解，其安全性相当于1次一密乱码本加密方式，它在信息论意义上是安全的，所以，不能恢复秘密。证毕。

4.3  子秘密再生性

由于算法是基于再生码的，因而，本方案的1个优点是：在某个分享者的秘密丢失时，可以不必与秘密分发者进行通信；秘密分发者完成秘密分发后就可以丢弃原始秘密，这也有利于秘密的安全性。丢失秘密的分享者只需到另外一些秘密分享者那里下载一定的数据块即可重建自己的子秘密。这一特点可以解决一些环境下分享者秘密丢失的问题，如P2P网络中某失效节点在重新加入系统时的秘密恢复等。

4.4  分享者的数据存储量

对于1个大小为M的秘密文件来说，本方案中每个分享者只需存储f+1的数据量，其中f=[M/t]。而对于SHAMIR方案^[5]，每个分享者都需要存储M数据量，因此，本方案可以节省存储空间。这对于一些存储能力有限的设备(如智能卡、无线传感器网络，移动互联网等)，布署该方案是十分有利的。

5  结论

1) 利用精确再生码构造了一种新的秘密共享方案，并以实例说明了方案中算法的具体实现。方案由子秘密的分发、原始秘密的恢复、子秘密丢失者的数据重建3个过程组成。

2) 与传统秘密共享算法相比，本方案具有安全性高、运算复杂性低、共享者的秘密份额可以再生、节点存储量小等特点。

3) 下一步研究的重点是精确再生码在云存储、无线传感器网络、移动互联网、ad hoc网络以及P2P网络等环境下的应用。

参考文献：

[1] MAO Bo, WU Suzhen, JIANG Hong. Improving storage availability in cloud-of-clouds with hybrid redundant data distribution[C]//Proceedings of the 29th IEEE International Parallel & Distributed Processing Symp(IPDPS’15). Piscataway, NJ: IEEE, 2015: 1-10.

[2] CHEN H C H, HU YUCHONG, LEE P P C, et al. NCCloud:A network-coding-based storage system in a cloud-of-clouds[J]. IEEE Transactions on Computers, 2014, 63(1): 31-44.

[3] 冯登国, 张敏, 张妍, 等. 云计算安全研究[J]. 软件学报, 2011, 22(1): 71-83.

FENG Dengguo, ZHANG Min, ZHANG Yan, et al. Study on cloud computing security[J]. Journal of Software, 2011, 22(1): 71-83.

[4] 冯朝胜, 秦志光, 袁丁. 云数据安全存储技术[J]. 计算机学报, 2015, 38(1): 150-163.

FENG Chaosheng, QIN Zhiguang, YUAN Ding. Techniques of secure storage for cloud data[J]. Chinese Journal of Computers, 2015, 38(1): 150-163.

[5] SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612-613.

[6] BLAKLEY G R. Safeguarding cryptographic keys[C]// Proceedings of AFIPS 1979 National Computer Conference. Monval, USA: AFIPS Press, 1979: 313-317.

[7] BEIMEL A, CHOR B. Secret sharing with public reconstruction[C]//COPPERSMITH D. Advances in Cryptology-CRYPTO ’95, LNCS 963. Berlin: Springer-Verlag, 1995: 353-366.

[8] PIEPRZYK J, ZHANG X M. On cheating immune secret sharing[J]. Discrete Mathematics & Theoretical Computer Science, 2004, 6(2): 253-264.

[9] GUO Y B, MA J F. Proactive secret sharing in synchronous networks with unreliable links[J]. Acta Electronica Sinica, 2004, 32(3): 399-402.

[10] 杨义先. MDS码在保密学中的应用[J]. 北京邮电学院学报, 1988, 11(1): 30-36.

YANG Yixian. The applications of MDS codes in cryptography[J]. Journal of Beijing University of Posts and Telecommunications, 1988, 11(1): 30-36.

[11] DIMAKIS A G, GODFREY P B, WU Y, et al. Network coding for distributed storage systems[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551.

[12] AHLSWEDE R, CAI N, LI S R, et al. Network information flow[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1204-1216.

[13] ASMUTH C, BLOOM J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, 29(3): 208-210.

[14] KARNIN E D, GREENE J W, HELLAN M E. On sharing secret systems[J]. IEEE Transactions on Information Theory, 1983, 29(3): 35-41.

[15] 王意洁, 孙伟东, 周松, 等. 云计算环境下的分布存储关键技术[J]. 软件学报, 2012, 23(4): 962-986.

WANG Yijie, SUN Weidong, ZHOU Song, et al. Key technologies of distributed storage for cloud computing[J]. Journal of Software, 2012, 23(4): 962-986.

[16] CHOU P A, WU Y, JAIN K. Practical network coding[C]//Proceedings of 41st Annual Allerton Conference on Information Control and Computing. Monticello, USA: Springer-Verlag, 2003: 214-218.

[17] FINCK T, HEINIG G, ROST K. An inversion formula and fast algorithm for Cauchy-Vandermonde matrices[J]. Linear Algebra and Its Applications, 1993, 183(1): 179-191.

[18] 王新梅, 肖国镇. 纠错码—原理与方法[M]. 修订版. 西安: 西安电子科技大学出版社, 2001: 178-179.

WANG Xinmei, XIAO Guozhen. Error correction codes-principle and method[M]. Revised ed. Xi’an: Xian University of Electronic Science and Technology Press, 2001: 178-179.

[19] PIEPRZYK J, ZHANG Xianmo. Ideal threshold schemes from MDS codes[C]//Proceedings of the 5th International Conference on Information Security and Cryptology. Berlin: Springer-Verlag, 2003: 253-263.

(编辑  陈灿华)

收稿日期：2016-06-20；修回日期：2016-08-26

基金项目(Foundation item)：国家自然科学基金资助项目(61173169, 61363037)；湖南省教育厅科研资助项目(13C755)(Projects (61173169, 61363037) supported by the National Natural Science Foundation of China;Project (13C755) supported by the Science Foundation of Education Department of Hunan Province)

通信作者：王伟平，博士，教授，从事网络编码、匿名通信等研究；E-mail：wpwang@csu.edu.cn