不同装置下点源球体的近似解与精确解对比
汤井田,原源
(中南大学 地球科学与信息物理学院,有色金属成矿预测教育部重点实验室,湖南 长沙,410083)
摘要:针对利用简单加倍的方法求解点源球体解析解的局限性,采用双球坐标系,通过镜像法求解点源下球体的精确解,将其与简单加倍求得的近似解进行对比,给出了简单加倍方法的适用条件,从而在实际中能够更准确地使用简单加倍的方法。研究结果表明:对于二极装置,当球心埋深h≤1.5r0时,利用简单加倍方法求得的近似解与精确解的误差已达到10%以上;对于中梯装置,当球心埋深h≤1.7r0时,二者的误差达到10%;二极装置的视电阻率曲线随着极距AM的增加会出现反向异常的现象,且极距越大,反向异常越明显。
关键词:点源;球体;视电阻率;反异常;电阻率法
中图分类号:P631.39 文献标志码:A 文章编号:1672-7207(2012)03-1057-08
Comparison of approximate solution and exact solution of buried sphere model at point source with different arrays
TANG Jing-tian, YUAN Yuan
(Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,
School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Abstract: In order to overcome the limitation of general method for the problem of a buried sphere with point source, based on bispheroid coordinate system, the exact solution was solved by image method. Through comparing the exact solution with approximate solution, the using condition of approximate solution was achieved and the general method could be better used in practice. The results show that the error between exact solution and approximate solution is more than 10% when the depth of sphere is less than 1.5r0 and being measured with pole-pole array. The error is more than 10% when the depth of sphere is less than 1.7r0 and being measured with schlumberger array. With the increase of electrode distance, the phenomenon of reversed anomaly appears in apparent resistivity curves of pole-pole array and the bigger the electrode distance is, the more obvious the phenomenon is.
Key words: point source; sphere; apparent resistivity; false anomaly; resistivity method
均匀半空间中点源下球体的精确解最初是由Webb[1]于1931年提出的,文中给出了电位三级近似的解析解;van Nostrand等[2]讨论了温纳装置下,点源球体的视电阻率异常随着球心埋深的变化规律;Dieter[3]通过面积分求得球体上感应电荷产生的电位,最终给出了视电阻率异常和极化率异常规律;Lipskaya等[4-6]推导了大地坐标系下的电位公式;Snyder等[7]讨论了点源不同埋深对视电阻率异常的影响;Singh等[8]针对球体电阻率为0 ?·m这一情况,利用点源多次镜像进行求解;朴化荣等[9]对该问题的严格解析解进行了理论计算并得到联剖装置下的视电阻率异常曲线。这些讨论主要从精度上进行了电位的求解及视电阻率异常计算,公式推导都非常复杂,且前人的讨论均在球心埋深h≥1.5r0(r0为球半径)的情况下进行的,对于埋深更浅的情况没有深入的研究。在实际中,更多的希望采用简单加倍的方法,以最小的代价来得到满足需要的结果,这就要对近似解和精确进行对比分析,得到简单加倍方法的适用条件。本文作者从点源球体精确解的公式推导出发,通过对比分析得到使用近似解时所必须满足的临界条件。此外,国内外很多学者利用该模型进行了数值计算[10-17],得到相对准确的结果,尽管如此,本文作者利用解析法求得该问题的精确解对于其他数值方法的进一步研究提供了一定的基础。
1 公式推导
利用解析法求解稳定电流场的电位是通过边界条件求解与实际问题相应的拉普拉斯方程。利用简单加倍求解该问题的近似解在电法教材中均有详细的公式推导,这里不再赘述。本文主要推导了利用镜像法求解精确解的过程。
图1所示为均匀半空间点源场中导电球体模型结构示意图。点源位于A处,电流强度为I,测点为M,点源与球心和测点的距离分别为D和R,球心与测点的距离为r,球心埋深为h0,球体电阻率为ρ1,半空间电阻率为ρ2。对于S系,点电流源A的直角坐标为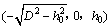 ,球坐标为
,球坐标为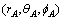 ,其中rA=D,θA=arcos(h0/D),
,其中rA=D,θA=arcos(h0/D),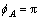 。任意点M(x, y, z)的镜像点为M′(x, y, 2h0-z)。S系中的球坐标为
。任意点M(x, y, z)的镜像点为M′(x, y, 2h0-z)。S系中的球坐标为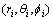 ,S′系中的球坐标为
,S′系中的球坐标为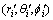 。
。
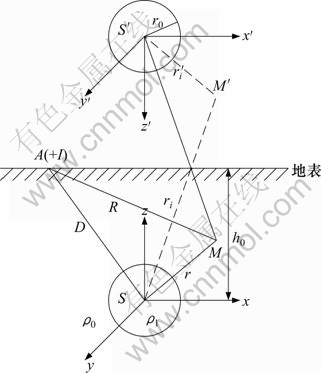
图1 均匀半空间点源场中导电球体模型结构示意图
Fig.1 Model sketch of buried sphere in homogeneous half-space
球外和球内的电位表达式为:
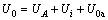 (1a)
(1a)
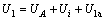 (1b)
(1b)
其中:Ui为镜像球S′产生的电位,点源A产生的电位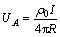 ,U0a和U1a分别为球内和球外的异常电位。
,U0a和U1a分别为球内和球外的异常电位。
球面S处有如下边界条件:
(1) r→∞,U0=0
(2) r→0,U1有限
(3) r=r0,U0=U1
(4) 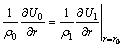
电位满足拉普拉斯方程:
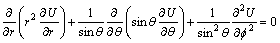 (2)
(2)
通过分离变量法求得电位的通解形式为:
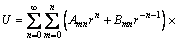
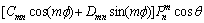 (3)
(3)
根据边界条件(1)和(2)得:
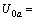
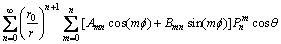 (4a)
(4a)
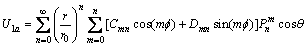 (4b)
(4b)
利用勒让德函数的加法公式
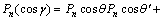
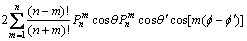 (5)
(5)
初次电位UA的表达式变换为:
(1) 当r<D时
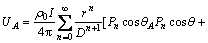
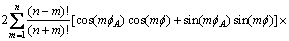
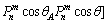 (6a)
(6a)
(2) 当r>D时
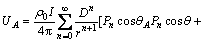
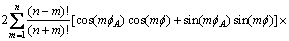
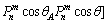 (6b)
(6b)
球S′ 在M点产生的电位Ui等于球S在对称点M′产生的电位。即
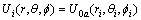 (7)
(7)
将式(7)代入式(4a)得

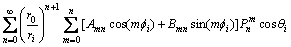 (8)
(8)
上式中的坐标是以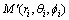 表示,由于S系中
表示,由于S系中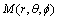 与S′系中
与S′系中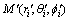 在数值上相等,因此,将
在数值上相等,因此,将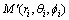 坐标变换为
坐标变换为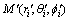 即得
即得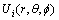 的表达式。
的表达式。
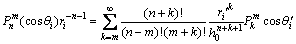 (9)
(9)
 (10)
(10)
将式(9)和式(10)代入式(8)并转化为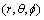 得
得
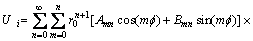
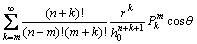 (11)
(11)
交换式(11)中n, k得
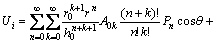
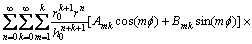
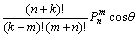 (12)
(12)
整理得:
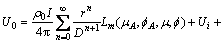
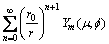 (13a)
(13a)
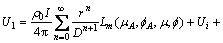
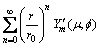 (13b)
(13b)
其中
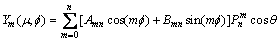 (14a)
(14a)
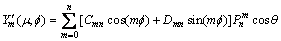 (14b)
(14b)
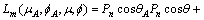
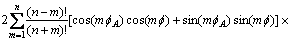
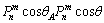 (15)
(15)
将边界条件(3)代入式(13a)和(13b)得:
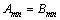 ,
,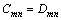
再利用边界条件(4),比较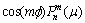 以及
以及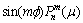 的系数得:
的系数得:
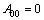 ,
, (16)
(16)
其中,
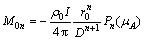 (17)
(17)
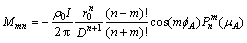 (18)
(18)
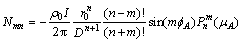 (19)
(19)
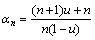 (20)
(20)
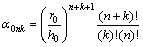 (21)
(21)
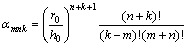 (22)
(22)
式(22)中的m,n和k值为:
当m=0时,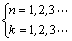
当m=1, 2, 3, …时,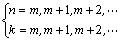
通过求解式(16)即得系数Amn和Bmn,代入式(13a)和(13b)即得空间任意一点的电位。
2 模型计算
2.1 收敛性分析
不论是用简单加倍求解近似解还是用镜像法求解精确解,最终电位都是无穷级数和的形式,为确定迭代次数,首先进行了收敛性分析。
表1所示为近似解的级数收敛性误差。从表1可看出:当模型参数一定,球心正上方处N阶和N+1阶的视电阻率绝对误差随阶数的增加逐渐减小;当求解阶数一定时,视电阻率差值随球心埋深的增加而减小,当h=1.3 m时,采用双精度求得的结果为0。由此,后文中对于简单加倍的求解级数均取N=50即可满足精度要求。
表1 近似解的级数收敛性误差表
Table 1 Error estimates for convergence of approximate solution

图2所示为球心埋深h=1.1 m时精确解的级数收敛性误差。其模型参数如下:背景电阻率为1 ?·m;球体电阻率为0.1 ?·m;球心埋深h为1.1 m;球半径r0为1 m;极距AM取0.5 m。从图2可看出:视电阻率级数随着N的增加逐渐趋于一稳定值,N=5和N=8的曲线已接近重合,因此,本文在对精确解进行求解时均取级数N=8。
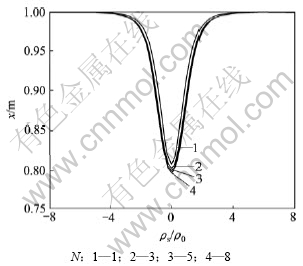
图2 精确解的级数收敛性误差
Fig.2 Error estimates for convergence of exact solution
2.2 二极装置下的视电阻率曲线
图3所示为二极装置下的地电模型结构示意图。模型参数如下:测区范围为-7~7 m;点距为0.25 m;二极装置的极距AM分别取0.5,1.0,1.5,2.0和2.5 m;球半径r0为1.0 m;球体与围岩电阻率之比分别取0.05,0.2和0.5;球心埋深h为1.1,1.5和2.0 m。视电阻率曲线如图4所示,从图4可看出:二极装置下点源球体(低阻球)的视电阻率均处于1以下,其曲线总体呈现先减小后增加的趋势,球心正上方的视电阻率取得极值。从附图中的每一幅视电阻率曲线(如图4(a)所示)可看出:视电阻率异常幅值随着极距AM的增大而增大,增大到一定程度后开始出现反异常的现象[18],而且反异常会随着极距的加大而更加明显,由此得到在实际中使用二极装置时,极距AM应小于球心埋深与球半径之比,否则会出现反异常的现象,影响资料的准确解释;由横向对比可知(如图4(a)~(c)所示):视电阻率异常的幅值会随着球心埋深的增加而减小;由纵向对比可知(如图4(a),4(d)和4(g)所示):视电阻率曲线的幅值会随着球体电阻率与围岩电阻率之比的增加而减小(注:对高阻球体而言这个规律刚好相反,即视电阻率曲线的幅值会随着球体与围岩电阻率之比的增加而增大)。
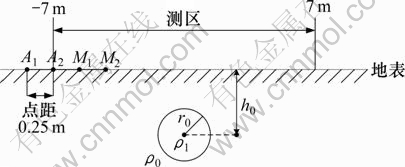
图3 二极装置下地电模型结构示意图
Fig.3 Sketch of geoelectricity model with pole-pole array
2.3 中梯装置下近似解与精确解的视电阻率曲线 对比
图5所示为中梯装置下的地电模型结构示意图。模型参数为:供电电极AB=50 m;测区范围为-7~7 m;点距为0.25 m;测量电极距MN分别取0.5,1.0,1.5,2.0和2.5 m;球半径r0=1.0 m;球体与围岩电阻率之比为0.05;球心埋深h=1.1 m。利用简单加倍求得的近似解与精确解的视电阻率曲线如图6所示。
从图6可看出:在给定的模型参数下,近似解和精确解的视电阻率曲线形态类似,均在球心正上方出现极小值,而在球体两侧出现极大值,但是近似解的异常幅值远大于精确解,且其在球心正上方的极小值小于0,而视电阻率不可能为负值,这显然说明了简单加倍的方法在球心埋深较浅时出现了严重的误差。
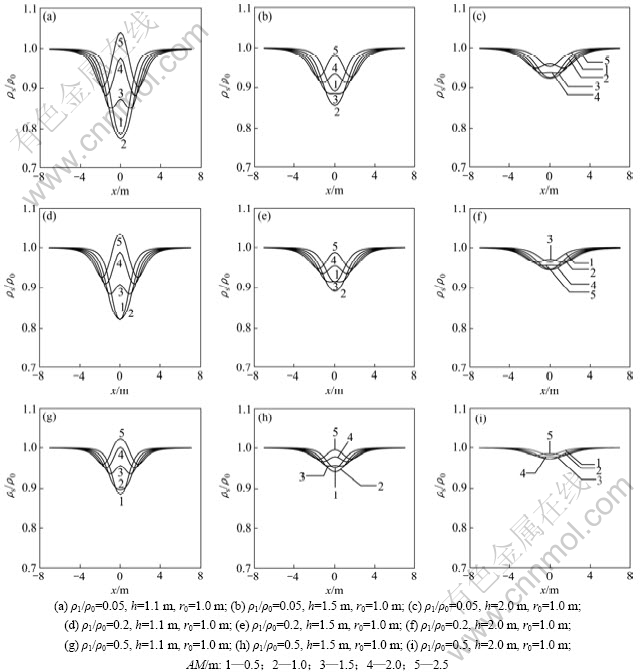
图4 二极装置下不同模型视电阻率曲线对比
Fig.4 Comparison of apparent resistivity curves for different models (pole-pole array)

图5 中梯装置下地电模型结构示意图
Fig.5 Sketch of geoelectricity model with schlumberger array
2.4 近似解与精确解的误差分析
对确定近似解的适用条件,本文进一步对近似解与精确解进行误差分析,通过定量计算得到临界深度。
图7所示为二极装置下近似解与精确解随球心埋深产生的误差分布。采用的模型是:电阻率之比ρ1/ρ0=0.1,球心埋深h=1.1,1.2,1.3,…,2.0 m,极距AM为0.5 m,球半径r0为1 m。从图7可看出:球心埋深对近似解与精确解的误差有很大影响,随着球心埋深变浅,二者的相对误差逐渐增大,当球心埋深为1.1 m时,二者在球心上方的相对误差已达到67.34%;当球心埋深为1.5 m时,相对误差为12.55%,此时可认为简单加倍的方法失效(本文认为近似解与精确解的相对误差超过10%时,简单加倍的方法失效);再者,从图7也可看出:误差的产生主要集中在球心上方附近,离球体越远处的误差就越小。
图8所示为中梯装置下近似解与精确解随球心埋深产生的误差分布图。采用的模型是:电阻率之比ρ1/ρ0=0.1,球心埋深h=1.1,1.2,1.3,…,2.0 m,极距MN=0.5 m,球半径r0=1 m。从图8可看出:球心埋深对近似解与精确解的误差会有很大影响,随着球心埋深变浅,二者的相对误差逐渐增大,当球心埋深为1.1 m时,二者在球心上方的相对误差已达到1.07(原因是中梯装置下简单加倍求得的视电阻率在球心上方是负值);当球心埋深为1.7 m时,二者在球心上方的相对误差为10.69%,此时可认为简单加倍的方法失效。再者,误差的产生主要集中在球心上方附近,从球心向两侧,相对误差呈现减小增大再减小的趋势。
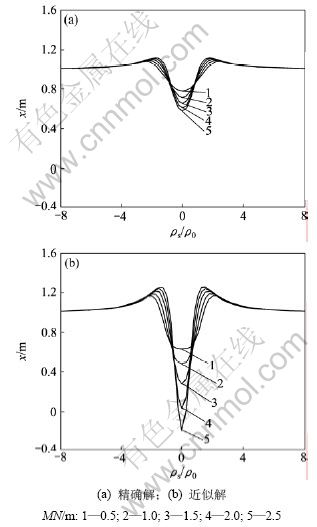
图6 中梯装置下近似解和精确解的视电阻率曲线对比
Fig.6 Comparison between apparent resistivity curves of approximate solution and exact solution with schlumberger array
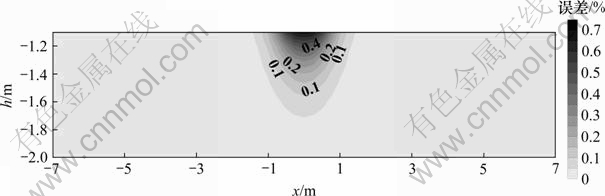
图7 二极装置下近似解与精确解随球心埋深产生的误差分布
Fig.7 Distribution map of apparent resistivity error calculated by pole-pole and changed with depth of sphere
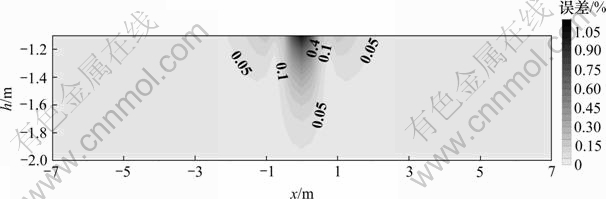
图8 中梯装置下近似解与精确解随球心埋深产生的误差分布
Fig.8 Distribution map of apparent resistivity error calculated by schlumberger array changed with depth of sphere
3 水槽试验
为进一步确定二极装置产生的反异常现象,本文进行了水槽试验。水槽试验示意图如图9所示。水槽尺寸(长×宽×高)为3.6 m×4.0 m×2.0 m,测区范围为-70~70 cm,点距为5 cm,石墨球的半径为10 cm,球顶埋深分别为3,5和10 cm,极距AM分别为10,14,20和30 cm。
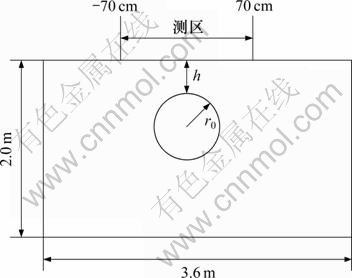
图9 水槽试验示意图
Fig.9 Sketch map of flume experiment
在上述模型参数下,采用二极装置测量得到的视电阻率曲线如图10所示。水槽试验结果表明:二极装置在大极距下确实会产生反异常,而且随着极距的增加,反异常也更加明显;反异常的产生也与球体埋深有关,在相同的测量条件下,球心埋深越浅越容易出现反异常。
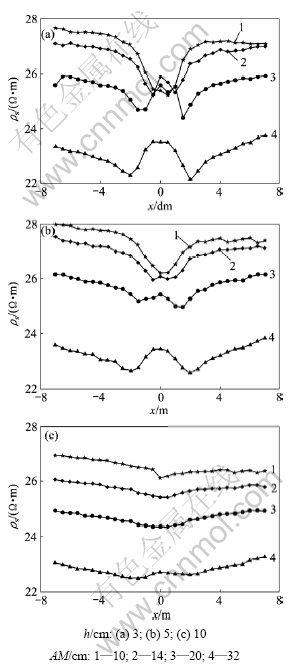
图10 不同球顶埋深及极距下的水槽试验结果
Fig.10 Flume experiment with different top depth of sphere and different space of electrode AM
4 结论
(1) 在模型参数一定的情况下,二极装置的视电阻率曲线随着极距AM的增加会出现反向异常的现象,极距越大,这种反向异常也就越明显。此外,反向异常的出现也与球心埋深有关,球心埋深越浅,反向异常也就越明显,从水槽试验中也可发现该规律。
(2) 中梯装置下,当球心埋深h=1.1r0时,简单加倍求得近似解的视电阻率在球心上方出现负值。该现象说明简单加倍的方法在球心埋深较浅时会出现很大的误差。
(3) 从误差分析结果得出:在二极装置下,当球心埋深h≤1.5r0时,近似解与精确解的误差已达到10%以上;而在中梯装置下,当球心埋深h≤1.7r0时,二者的误差达到10%。因此,在实际情况中,当球心埋深在临界深度以内时不可采用简单加倍的方法进行近似计算。
参考文献:
[1] Webb J H. Potential due to a buried sphere[J]. Physical Review, 1931, 37: 292-302.
[2] van Nostrand R G. Limitations on resistivity methods as inferred from buried sphere problem[J]. Geophysics, 1953, 20: 423-433.
[3] Dieter K. IP and resistivity type curves for three-dimensional bodies[J]. Geophysics, 1969, 34(4): 615-632.
[4] Lipskaya N V. The disturbance of electrical fields by spherical inhomogeneities(method of dipolar coordinates)[J]. Acad Nauk SSSR Izv Ser Geog Igeofiz, 1949, 13(2): 335-347.
[5] Merkel R H, Alexander S S. Resistivity analysis for models of a sphere in a half-space with buried current sources[J]. Geophysical Prospecting, 1971, 19(4): 640-651.
[6] Large D B. Electrical potential near a spherical body in a conducting half-space[J]. Geophysics, 1971, 36(4): 763-767.
[7] Snyder D D, Merkel R M. Analytic models for the interpretation of electrical surveys using buried current electrodes[J]. Geophysics, 1973, 38(3): 513-529.
[8] Singh S K, Espindola J M. Apparent resistivity of a perfectly conducting sphere buried in a half-space[J]. Geophysics, 1976, 41(4): 742-751.
[9] 朴化荣, 曲增芳, 李晓波. 点电源场中埋没球的正演及数值计算—电法勘探文集[M]. 北京: 地质出版社, 1986: 65-75.
PIAO Hua-rong, QU Zeng-fang, LI Xiao-bo. The forward modeling and numerical calculation of a buried sphere in a point source[M]. Beijing: Geological Publishing House, 1986: 65-75.
[10] 徐淳宁. 常用场源激励下椭球体电阻率的数值计算[J]. 长春理工大学学报, 2008, 31(3): 144-146.
XU Fu-ning. The numerical calculation of the apparent resistivity curve of ellipsoid under normal field source[J]. Journal of Changchun University of Science and Technology, 2008, 31(3): 144-146.
[11] LI Yu-guo. Three-dimensional DC resistivity forward modeling using finite elements in comparison with finite-difference solutions[J]. Geophys J Int, 2002, 151: 924-934.
[12] 徐世浙. 复杂地电条件下点源三维电阻率模拟的新方法[J]. 物化探计算技术, 1991, 13(1): 13-20.
XU Shi-zhe. A new method for modeling the resistivity surveys with point source on 3-D arbitrary nonhomogeneous geoeletrical section[J]. Geophysical and Geochemical Exploration, 1991, 13(1): 13-20.
[13] 熊彬. 复杂条件下直流电阻率异常三维数值模拟研究[J]. 地质与勘探, 2003, 39(4): 60-64.
XIONG Bin. 3-D numerical simulation study of DC resistivity anomaly under complicated terrain[J]. Geology and and Prospecting, 2003, 39(4): 60-64.
[14] 徐世浙. 电阻率法中求解异常电位的有限单元法[J]. 地球物理学报, 1994, 37(1): 511-515.
XU Shi-zhe. The finite element method for solving anomalous potential for resistivity surveys[J]. Chinese journal of Geophysics, 1994, 37(1): 511-515.
[15] 乔中林. 直流电法三维正演多重网格算法研究[D]. 北京: 中国地质大学地球物理与信息技术学院, 2007: 30-33.
QIAO Zhong-lin. Study of 3-D forward of DC resistivity method using Multi-grid method[D]. Beijing: China University of Geosciences. School of Geophysics and Information Technology, 2007: 30-33.
[16] Lee T. An integral equation and its solution for some two- and three-Dimensional problems in resistivity and induced polarization[J]. Geophys J R Astr Soc, 1975, 42(1): 81-95.
[17] 徐世浙. 水平地形三维电场的边界单元法[J]. 物化探计算技术, 1984, 6(3): 53-60.
XU Shi-zhe. The boundary method for solving tile three dimensional electric field under the conditions of horizontal ground[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1984, 6(3): 53-60.
[18] 冯兵, 张兴安, 李有青. 高密度电法中的“异常扩展效应”及归位计算方法[J]. 物探与化探, 2004, 28(4): 349-351.
FENG Bing, ZHANG Xing-an, LI You-qing. The anomaly spreading effect in high density electric method and the technique for return-to-the-original-position calculation[J]. Geophysical and Geochemical Exploration, 2004, 28(4): 349-351.
(编辑 陈爱华)
收稿日期:2011-04-12;修回日期:2011-07-06
基金项目:国家自然科学基金资助项目(40874072)
通信作者:原源(1989-),女,山西运城人,硕士,从事三维直流电阻率有限元正反演研究;电话:13657400521;E-mail: yuanyuan.2126@yahoo.com.cn