DOI: 10.11817/j.issn.1672-7207.2015.07.018
基于窄带电力噪声干扰的OFDM分组检测算法
谷志茹,刘宏立,陈炳权,谭周文
(湖南大学 电气与信息工程学院,湖南 长沙,410082)
摘要:针对电力噪声和正交频分复用(orthogonal frequency division multiplexing,OFDM)信号的特点,为提高检测的准确度同时减少数据冗余,基于含噪信号本元分析,分解干净信号和电力噪声特征向量,根据噪声和信号空间能量的不同,利用本元滤波的方法检测数据分组的起点。在电力噪声和基于G3方案的OFDM模型下,通过对经典延时相关检测算法和本元滤波检测算法进行性能评测比较,结果显示在不同信噪比下,本元滤波检测算法对接收信号的起点检测更准确,相应系统的误码率得到降低。
关键词:电力线通信;正交频分复用;本元分析
中图分类号:TM73 文献标志码:A 文章编号:1672-7207(2015)07-2510-07
Packet detection algorithm of OFDM with narrow-band power line noise interference
GU Zhiru, LIU Hongli, CHEN Bingquan, TAN Zhouwen
(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)
Abstract: Considering the characteristics of power line noise and orthogonal frequency division multiplexing (OFDM) signal, a principal component analysis (PCA) was proposed for improving the accuracy of detection. This algorithm decomposes noisy signal into its principal components along the axes of a vector space of clean speech. To obtain the packet detection, the principle component filter was used. Through the evaluation to classic delay-and-correlate algorithm and the principle component filter algorithm for packet detection were compared. The results show that the principle component filter algorithm is more accurate for the OFDM signal detection, therefore, the algorithm can decrease the bit error rate (BER) of the system effectively.
key words: power line communication; orthogonal frequency division multiplexing; principal component analysis
转变当前电网成为一种交互式(需求/响应)的智能电网,能够改进现有电能传输的有效性、安全性和可靠性。作为构建智能电网的基础,先进计量体系(advanced metering infrastructure,AMI)[1]保证用户实时监测和修正网络,这就要求电网的控制中心和所管理的每个表计具有高速的双向通信能力。基于电力信道的通信技术,在与传递电能同一路径的线路上确定通信链路,传递信息,不需要重新铺设专用的通信通路,投入少,且电力线通信不会像有线的方式那样被密集的建筑物所阻挡,从而减少安装和维护费用,是智能电网(smart grid)[2]建设的主要通信方式。在长期单载波电力线通信技术(power line communication, PLC)长期垄断电力线通信技术市场,最近,窄带高速OFDM电力线载波通信技术在AMI系统中引起重视,如IEEE1901.2和ITU-T G.hnem这2个标准[3-4]着重于OFDM电力载波通信技术的规范。PRIME(powerline intelligent metering evolution)和G3-PLC[5]是2种非标准的表计和集中器间窄带OFDM电力载波技术解决方案,工作在10~95 kHz窄带,提供高的通信速率、鲁棒的通信模式,这些是智能电网双向通信的关键。由于电力线最初设计是用来在50~60 Hz频率范围传输电能,一方面作为信息传输媒介进行数据或语音传输的通信通路,电力线具有负荷情况复杂、信号衰减大,信道容量小等不足,并存在背景噪声、随机脉冲噪声、与工频同步的谐波噪声等;另一方面,OFDM技术提供高的通信速率和复杂的纠检错算法,要求大数据量传输。因此,对于适用于扩频-频率键控(the spread frequency-shift keying, S-FSK)技术的工频过零点同步方式[6]并不适用于OFDM技术。研究者多采用插入前导序列方法进行符号同步。Cooper[7]提出用一种二进制单极性伪随机序列作为前导序列,在频域产生且相位固定。前导序列符号同步是利用其周期延时相关性来检测数据分组的起点,在高斯白噪声的环境下,该算法可以较好地实现分组检测,但在非高斯的电力噪声干扰下,判决变量Mn由于受到信道中较大随机噪声的影响而超过预先设定的门限值,从而产生误判。为此,本文作者分析电力环境实际测量的噪声,建立10~95 kHz窄带,包括背景噪声和脉冲噪声[8]的非高斯分布噪声模型。基于此噪声,针对OFDM数据特点,应用本元成分分析,分解噪声和信号特征值和特征矢量,并利用本元滤波确定数据的起点,与经典相关检测算法进行评测。
1 噪声模型
分组同步是找寻数据分组起始的近似估算,是接收机工作的第1步。由于OFDM发射机和接收机工作非同步性,在数据分组到来前附加有额外的噪声;在数据分组结束后,又有一定的噪声,接收数据本身是数据与噪声的叠加。
在频率为 10~95 kHz的窄带,背景噪声的功率密度随着频率的增高而减小,如图1所示。所以,在较低频率传输数据时,受到低信噪比(signal to noise ratio, SNR)的限制;脉冲噪声主要包括同步和异步脉冲,能够产生较高能量,并且其周期可能超过几个符号。基于电力线信道模型[9],可以得到如下接收信号:
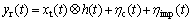 (1)
(1)
其中: 为接收信号;
为接收信号; 为发送信号;
为发送信号; 为多径衰落信道传输函数,本文按照Zimmerman模型建立[10];
为多径衰落信道传输函数,本文按照Zimmerman模型建立[10]; 为背景噪声;
为背景噪声; 为脉冲噪声。为得到有效的电力噪声模型,选湖南大学13舍实验楼作为测试点,对第7楼配电箱A相分时段对连续噪声进行测量记录,根据用电负荷不同,分成3个时段进行测量:
为脉冲噪声。为得到有效的电力噪声模型,选湖南大学13舍实验楼作为测试点,对第7楼配电箱A相分时段对连续噪声进行测量记录,根据用电负荷不同,分成3个时段进行测量:
轻量噪声时段,00:00—06:00;
中量噪声时段,12:00—13:00;
重量噪声时段,14:00—17:00。
测量总时长为6 361 min,约106 h,其中脉冲利用峰值检测器检出。
图1所示为背景噪声功率谱密度经平滑处理后的结果,其具有低通特性,所以,背景噪声的时域模型 可以由加性高斯白噪声(additive white Gaussian noise, AWGN)
可以由加性高斯白噪声(additive white Gaussian noise, AWGN) 通过升余弦滚降滤波器而得到。
通过升余弦滚降滤波器而得到。 的功率谱密度为n0,通过测试数据统计和中心极限定律分析,n0近似服从高斯分布:n0~N(-21.5, 2.0),其中N表示高斯分布函数。
的功率谱密度为n0,通过测试数据统计和中心极限定律分析,n0近似服从高斯分布:n0~N(-21.5, 2.0),其中N表示高斯分布函数。

图1 平滑后的背景噪声
Fig. 1 Background noise after being smoothed
图2所示为实测脉冲噪声的时域波形。显然,每个脉冲可由3个特性参数即包络av、宽度tw和间隔td描述,其脉冲函数表述如下[11]:
 (2)
(2)
其中:N为脉冲总数;t a,i为脉冲噪声的到达时间,由脉冲的宽度和间隔决定。
 (3)
(3)
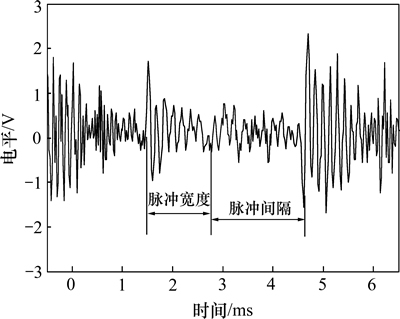
图2 脉冲噪声
Fig. 2 Impulsive noise
由图3可知:脉冲噪声具有指数衰减的正弦波振荡特性。基于式(2)和(3),特性参数tw,td,av和脉冲的总数N完全确定了脉冲噪声的时域波形。对于周期性脉冲,时间参数的确定比较直观;对于异步脉冲,这些参数是服从一定分布律的随机变量,由时域测量数据的统计分析得到。
为确定脉冲的参数,取观察时长为1 s,定义在此时间内脉冲的总数/1 s为冲激率rimp,脉冲的总时长/1 s为干扰率dr,得到测量数据的统计值见表1。
表1 测量数据的冲激率和干扰率
Table 1 Impulse rate and disturbance ratio of measurement

rimp和dr可以用下式表达:
 (4)
(4)
式中:NA和NP分别为异步脉冲和周期脉冲的个数。结合式(4),可以通过脉冲的来源和数量对表1所示结果进行解释。在重噪声时段,因为是工作时段,供电电源以同步于工频电压主频的速度持续动作,所以,大量短时宽的周期脉冲占主导,既使脉冲的平均个数达到161个,但所占时间仍然不足总时长的2%;在轻量噪声时段,实验楼内没有大量的用电设备,这时会存在开关的瞬态过程,所以,大部分是异步脉冲,周期脉冲可以忽略。在由“轻量噪声时段”进入“重量噪声时段”,周期性脉冲迅速增加。因为测量是在同一点位置进行的,所以,3组时段异步脉冲的个数保持不变。基于此NA,NP和周期脉冲的宽度tw_p可以推导如下:
 (5)
(5)
式中: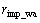 和
和 分别为轻量噪声组冲激率和干扰率的统计平均值,在表1中可以查表得到。异步脉冲噪声的特性参数tw,td和av的测量统计,其变化趋势近似指数分布,所以,用分段马氏链[6]描述。
分别为轻量噪声组冲激率和干扰率的统计平均值,在表1中可以查表得到。异步脉冲噪声的特性参数tw,td和av的测量统计,其变化趋势近似指数分布,所以,用分段马氏链[6]描述。
2 基于OFDM的分组检测算法
比较现有适合AMI应用的两大OFDM电力载波方案G3-PLC和PRIME[12],OFDM工作均在CENELEC A(10~95 kHz)频段。基带有3种映射方式即DBPSK,DQPSK和D8PSK,但G3比PRIME多1种鲁棒的映射方式,以适应恶劣的电力环境,所以,选择G3-PLC的物理层作为OFDM系统模型。
2.1 OFDM信号
G3-PLC符号的N个子载波由K个数据子载波和N-K个空子载波组成,数据子载波共有36个,分布于35.9~90.6 kHz的频率范围内,其中,经过基带映射前的符号均为实数。经过基带映射后的符号有同相分量和正交分量,令 表示频域第m个符号的第k个子载波,其映射公式如下:
表示频域第m个符号的第k个子载波,其映射公式如下:
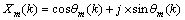 (6)
(6)
 根据3种映射方式的星座图确定。对第m个OFDM符号的发送信号,通过对式(5)进行离散傅里叶逆变换得到
根据3种映射方式的星座图确定。对第m个OFDM符号的发送信号,通过对式(5)进行离散傅里叶逆变换得到
 (7)
(7)
其中: 表示第m个OFDM符号的第n个时域信号;
表示第m个OFDM符号的第n个时域信号; 表示第k个数据子载波。在信号的开始增加30点循环前缀(cyclic prefix, CP)。OFDM的第m个通过电力信道的符号可以表示为
表示第k个数据子载波。在信号的开始增加30点循环前缀(cyclic prefix, CP)。OFDM的第m个通过电力信道的符号可以表示为
 (8)
(8)
式中: 表示长度为L的信道传输函数;
表示长度为L的信道传输函数; 为脉冲噪声的离散值;
为脉冲噪声的离散值;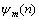 为背景噪声的离散值。由于发送和接收不同步,接收机首先接收到
为背景噪声的离散值。由于发送和接收不同步,接收机首先接收到 点采样噪声,分组检测的目的即确定
点采样噪声,分组检测的目的即确定 。当检测误差在CP保护间隔的允许范围内,除了零频外,其他子载波定时偏差会导致接收码元的相位旋转,可由信道估计的频域均衡来修正。
。当检测误差在CP保护间隔的允许范围内,除了零频外,其他子载波定时偏差会导致接收码元的相位旋转,可由信道估计的频域均衡来修正。
2.2 经典分组检测算法
传统应用于电力线载波通信的分组检测算法[9]利用前导符号的周期性实现延时相关。假定噪声为不相关的高斯白噪声,算法按如下公式实现:
 (9)
(9)
式中:Cn为接收信号 的延迟相关;Pn为接收信号
的延迟相关;Pn为接收信号 的能量;Mn为延迟相关算法的判决变量。当计算延迟相关的2个滑动窗进入数据分组的前导序列时,Mn会出现峰值。在其他时间,由于噪声的非相关性,Mn比较小。所以,设定判决门限Thd,当Mn>Thd时利用第1点出现的峰值来判断数据分组的到来。在高斯白噪声的环境下,延迟相关算法可以较好地实现分组检测,但在非高斯的电力噪声干扰下,判决变量Mn由于受到信道中较大随机噪声的影响而超过预先设定的门限值,从而错误地判断有分组到来。为了降低误判率,必须对经典分组检测算法进行改进。
的能量;Mn为延迟相关算法的判决变量。当计算延迟相关的2个滑动窗进入数据分组的前导序列时,Mn会出现峰值。在其他时间,由于噪声的非相关性,Mn比较小。所以,设定判决门限Thd,当Mn>Thd时利用第1点出现的峰值来判断数据分组的到来。在高斯白噪声的环境下,延迟相关算法可以较好地实现分组检测,但在非高斯的电力噪声干扰下,判决变量Mn由于受到信道中较大随机噪声的影响而超过预先设定的门限值,从而错误地判断有分组到来。为了降低误判率,必须对经典分组检测算法进行改进。
2.3 基于本元滤波的分组检测算法
电力噪声可以看成是背景噪声和脉冲噪声的叠加,这是2种具有不同分布特性的噪声。在数据分组检测前,首先对非平稳脉冲噪声使用无记忆非线性技术(限幅、消隐)[13-14]进行滤波,以克服脉冲噪声对分组检测的影响,然后,利用本元滤波[15-16]的方法检测数据分组的起点。
OFDM时域信号根据式(6)和(7)写为

 (10)
(10)
因OFDM输入数据是零均值随机变量,所以,经基带映射后其实部和虚部仍为零均值随机变量。IFFT变换因子 可以看成K维复基矢量:
可以看成K维复基矢量:

所以,OFDM信号满足线性模型: [14],其秩为K。脉冲噪声滤波后,剩余脉冲噪声平稳分布于门限附近,其分布可近似为背景噪声。假设信道均衡理想,
[14],其秩为K。脉冲噪声滤波后,剩余脉冲噪声平稳分布于门限附近,其分布可近似为背景噪声。假设信道均衡理想,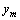 可以表示为
可以表示为
 (11)
(11)
式(11)表示每个符号取N个数据点,在 ≤
≤ 之前进入接收机的都是噪声。显然,OFDM信号和背景噪声满足各态历经性。因OFDM信号线性模型的秩为K,所以,构造
之前进入接收机的都是噪声。显然,OFDM信号和背景噪声满足各态历经性。因OFDM信号线性模型的秩为K,所以,构造 Hankel矩阵
Hankel矩阵 [17]。
[17]。
 (12)
(12)
其中:N=K+W-1。
每帧接收信号的自相关矩阵表示如下:
 (13)
(13)
其中: ;Q和
;Q和 分别为其特征矢量和特征值矩阵。令q1, q2, …, qK是相应特征值λ1, λ2, …, λK的特征矢量,则Q可以表示为
分别为其特征矢量和特征值矩阵。令q1, q2, …, qK是相应特征值λ1, λ2, …, λK的特征矢量,则Q可以表示为
 (14)
(14)
由于噪声和干净的OFDM信号是不相关的,所以,沿着每个特征矢量方向的含噪信号能量等于干净信号能量与噪声能量的和:
 (15)
(15)
式中: 为接收信号特征矩阵;
为接收信号特征矩阵; 干净信号特征值矩阵;
干净信号特征值矩阵;  为噪声信号特征值矩阵。
为噪声信号特征值矩阵。
投影至第i个特征矢量的含噪信号平均能量表示如下:
 (16)
(16)
其中:0≤ ≤1,为平滑因子;
≤1,为平滑因子; 为前一特征矢量投影能量;
为前一特征矢量投影能量; 为当前特征矢量投影能量。这是一种子空间能量跟踪方法[18],每个符号的本元能量为
为当前特征矢量投影能量。这是一种子空间能量跟踪方法[18],每个符号的本元能量为
 (17)
(17)
则本元滤波可以设计如下:
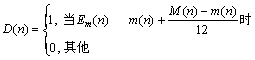 (18)
(18)
其中:

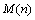 和
和 分别为最大和最小滤波能量;
分别为最大和最小滤波能量; 为滤波器的平滑因子;D(n)为分组同步检测值,1为数据分组到来,0为噪声,默认为0。
为滤波器的平滑因子;D(n)为分组同步检测值,1为数据分组到来,0为噪声,默认为0。
3 算法评测
在MATLAB环境下,按照G3-PLC标准产生前导数据,并按照电力噪声模型产生噪声信号,在分组起点Pstart=1 000和n0=-30~-10 dB的噪声功率下,前导数据和噪声信号组合成为接收信号共100个数据分组,分别评测经典算法和新算法的性能。新算法参数及初始值设置如下:
 ,
, ,
,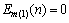
图3所示为n0为-30 dB和-10 dB条件下经典算法和新算法的分组检测起点,其中黑色实线代表真实的数据分组起点,即Pstart=1 000,实线代表新算法所检测起点值,虚线代表经典算法所检测起点值。从图6可以看出:在-10 dB电力环境中,新算法的检测结果的最大检测值为1 257,最小检测值为812;而经典算法的最大检测值为1 570,最小检测值为317,均比新算法的检测结果距离真值较大。所以,新算法与经典算法相比,其检测结果更加收敛于真实分组起点Pstart。这是因为经典算法根据延迟相关的能量变化来检测分组的起点,并设置判决门限,所以,在电力噪声比较低的情况下,其判决误差较大,结果较发散;而新算法利用本元分解及空间能量跟踪滤波的方法来检测数据分组的起点,提高了算法检测的准确性。同时,从图6中可知-30 dB电力噪声功率下的检测结果比-10 dB的检测结果收敛,这同样说明了新算法对不同干扰环境的适应性。
表2所示为2种电力噪声功率下对检测误差分析结果。其均方误差ERMS[19]的计算式为
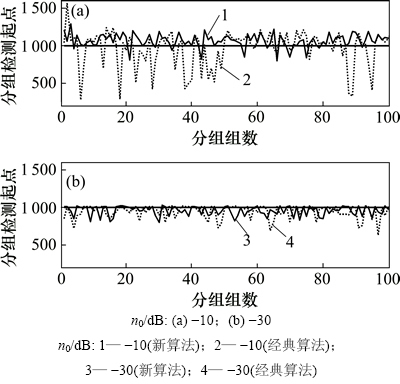
图3 2种算法检测起点比较
Fig. 3 Results comparison of two algorithms
 (19)
(19)
其中:Dv为检测值;Rv为真值。在-10 dB时,新算法的均方误差为14.55,而经典算法为43.34,经典算法的均方误差比新算法的均方误差高3倍多;在-30 dB时,新算法的均方误差为6.73,而经典算法的为21.93,同样经典算法的均方误差比新算法的均方误差也高3倍多:所以,在相同的电力噪声功率下,新算法的均方误差比经典算法的均方误差小很多,这说明新算法对数据分组起点的检测比经典算法的检测准确性高。
表2 新算法及经典算法检测误差比较
Table 2 Comparison of mean square error of two algorithms

假定相应频率的信道增益 ,G3-PLC信号的平均功率一致,表示为
,G3-PLC信号的平均功率一致,表示为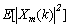 。窄带电力噪声的平均功率主要由背景噪声功率决定,背景噪声模型由功率谱密度为n0的AWGN,通过升余弦低通滤波器得到,由此得到接收端的含噪信号信噪比RSN为[20]
。窄带电力噪声的平均功率主要由背景噪声功率决定,背景噪声模型由功率谱密度为n0的AWGN,通过升余弦低通滤波器得到,由此得到接收端的含噪信号信噪比RSN为[20]
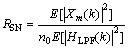 (20)
(20)
其中: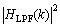 为升余弦低通滤波器的增益值。图4所示为RSN为-6~6 dB时,2种算法100个数据分组的检测起点Pstart均值比较。从图4可见:在-6 dB时,新算法的Pstart均值为979,而经典算法为967,经典算法的均值比新算法的大;在6 dB时,新算法的Pstart均值为994,而经典算法的均值为981,同样经典算法比新算法的均值高。所以,多个数据分组检测起点Pstart求平均后,检测结果更逼近真实起点,并且新算法比经典算法更准确,在低信噪比环境中依然适用。图5所示为2种检测算法在G3-PLC系统中的误码率RBE比较结果。
为升余弦低通滤波器的增益值。图4所示为RSN为-6~6 dB时,2种算法100个数据分组的检测起点Pstart均值比较。从图4可见:在-6 dB时,新算法的Pstart均值为979,而经典算法为967,经典算法的均值比新算法的大;在6 dB时,新算法的Pstart均值为994,而经典算法的均值为981,同样经典算法比新算法的均值高。所以,多个数据分组检测起点Pstart求平均后,检测结果更逼近真实起点,并且新算法比经典算法更准确,在低信噪比环境中依然适用。图5所示为2种检测算法在G3-PLC系统中的误码率RBE比较结果。

图4 2种算法检测起点均值比较
Fig. 4 Average value comparison of two algorithms
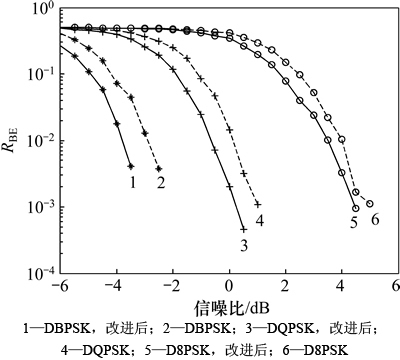
图5 2种算法的误码率RBE比较
Fig. 5 RBE comparison of two algorithms
当RSN为-6~6 dB时,对G3-PLC的3种基带映射方式进行性能评价,如图5所示。其中,实线为OFDM接收机的输出数据与原始数据比较得到的RBE曲线,输出数据是由本文算法的数据进行G3相关解调译码处理得到的;虚线为经典算法数据进行G3相应处理得到的输出数据与原始数据比较得到的误码率RBE曲线。从图5可以看出:新算法检测数据的RBE明显比经典算法检测的高。例如对于DBPSK映射方式,新算法检测后在RSN为-3 dB时,其误码率RBE为0,而经典检测算法在-2 dB左右才为0,性能提高了1 dB。
4 结论
1) 利用限幅非线性技术来减轻脉冲噪声的影响,应用本元分析和滤波方法检测数据分组的起点。
2) 为评测算法的性能,基于G3-PLC方案的物理层,建立OFDM系统的发射机和接收机,根据实际测量电力噪声的统计分析,提出基于随机分布的特性参数所描述的噪声模型。
3) 算法的检测结果和均方误差表明,本文所提出的算法改善了分组检测的性能。
参考文献:
[1] Mark S T. A aynergistic approach to implement demand response, asset management and service reliability using smart metering, AMI and MDM systems[C]// The 2009 IEEE PES General Meeting Advance Program of Technical Sessions and Committee Meetings. Alberta, Canada, 2009: 1-4.
[2] Fang X, Misra S, Xue G, et al. Smart grid-the new and improved power grid: A survey[J]. IEEE Communication Surveys Tutorials. 2012, 14(4): 944-980.
[3] IEEE 1901.2, IEEE Standard for low-frequency (less than 500 kHz) narrowband power line communications for smart grid applications[S].
[4] ITU-T G.9960, TU-T G.9961 transceivers for smart grid applications: advanced metering infrastructure, energy management in the home and electric vehicles[S].
[5] Javier M, Sadot A, Rodriguez-Morcillo C. Performance evaluation of two narrowband PLC systems: PRIME and G3[J]. Computer Standards & Interfaces, 2013, 36(1): 198-208.
[6] IEC 61334-5-1, Distribution automation using distribution line carrier systems Part 5-1: Lower layer profiles-The spread frequency shift keying (S-FSK) profile[S].
[7] Cooper D. Low-data-rate narrow-band power-line communication on the European domestic mains: Symbol timing estimation[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 111-118.
[8] Gotz M, Rapp M, Dostert K. Power line channel characteristics and their effect on communication system design[J]. IEEE Communications Magazine, 2004, 42(4): 78-86.
[9] Andreadou N, Pavlidou F N. Modeling the noise on the OFDM power-line communication system[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 150-157.
[10] Zimmermann M, Dostert K. A multipath model for the power line channel[J]. IEEE Transactions on Communications, 2002, 50(4): 555-559.
[11] Zimmermann M, Dostert K. Analysis and modeling of impulsive noise in broad-band powerline communications[J]. IEEE Transactions on Electromagnetic Compatibility, 2002, 44(1): 249-258.
[12] Javier M, Sadot A, Rodriguez-Morcillo C. Performance evaluation of two narrowband PLC systems: PRIME and G3[J]. Computer Standards & Interfaces, 2013, 36(1): 198-208.
[13] 何世彪, 王杰强, 韩彥净, 等. OFDM低压电力线通信系统的符号同步及其FPGA实现[J]. 电子技术应用, 2012, 38(4): 94-97.
HE Shibiao, WANG Jieqiang, HAN Yanjing, et al. Symbol synchronization for low-voltage on OFDM and its power line communication system based FPGA implementation[J]. Application of Electronic Technique, 2012, 38(4): 94-97.
[14] Korki M, Hosseinzadeh N. Performance evaluation of a narrowband power line communication for smart grid with noise reduction technique[J]. IEEE Transactions on Consumer Electronics, 2011, 57(4): 1598-1606.
[15] Kim Y, J Nam Bae, J Young Kim. Performance of power line communication systems with noise reduction scheme for smart grid applications[J]. IEEE Transactions Consumer Electronics, 2011, 57(1): 46-52.
[16] Amin H, S Sid-Ahmed, Douglas. Speech enhancement using PCA and variance of the reconstruction error in distributed speech recognition[C]// ASRU IEEE workshop on Digital Object Identifier. Kyoto, 2007: 19-23.
[17] Adda S, Abderrahmane A, Sid-Ahmed S. MCRA noise estimation for KLT-VRE-based speech enhancement[J]. International Journal of Advanced Manufacturing Technology, 2013, 16(3): 333-339.
[18] Ephraim Y, van Trees H L. A signal subspace approach for speech enhancement[J]. IEEE Transactions on Speech Audio Processing, 1995, 3(4): 251-266.
[19] 杨淑平, 易国栋, 袁修贵, 等. 一种基于分块小波的人脸识别算法[J]. 中南大学学报(自然科学版), 2013, 44(5): 1902-1909.
YANG Shuping, YI Guodong, YUAN Xiugui, et al. A face recognition algorithm based on blocking wavelet transforms[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 1902-1909.
[20] 张进, 赵文栋, 彭来献, 等. 相对误差受限的数据流流量测量算法[J]. 计算机科学, 2013, 40(6): 80-83.
ZHANG Jin, ZHAO Wendong, PENG Laixian, et al. Per-flow traffic measurement algorithm with restrained relative error[J]. Computer Science, 2013, 40(6): 80-83.
(编辑 陈灿华)
收稿日期:2014-09-10;修回日期:2014-11-15
基金项目(Foundation item):国家自然科学基金资助项目(61172089);高等学校博士学科专项科研基金资助项目(20120161120012);湖南省科技计划项目(2014WK3001) (Project(61172089) supported by the National Natural Science Foundation of China; Project(20120161120012) supported by the Special Scientific Research Foundation of the Doctoral Program of High University; Project(2014WK3001) supported by Hunan Science and Technology Plan)
通信作者:刘宏立,教授,博士生导师,从事电力通信、无线传感网络研究;E-mail: equilibria@163.com