蓄洪期路基边坡的含水特性
贺炜,付宏渊,严志伟
(长沙理工大学 岩土与隧道工程系,湖南 长沙,410114)
摘要:基于蓄洪区路基边坡在使用期经常受洪水浸泡,对路基边坡含水量的影响进行研究。首先定性分析正常使用期及蓄洪期各种环境的影响,在此基础上,引入Richards方程并根据Galerkin加权残量原理建立非饱和土非稳态流有限元格式,采用Dirichlet条件模拟边坡浸水的常水头条件;然后,引入Fredlund提出的非饱和土土水特征曲线模型及基于该模型导出的非饱和土渗透曲线预测方法,对实际工程土进行计算分析,获得相关计算参数。应用该方法对蓄洪条件下路基边坡的孔压及含水量分布进行计算分析。研究结果表明:蓄洪条件下路基可在较短的时间内达到稳定流状态,在工程设计中有必要考虑含水量变化引起的路基边坡问题。
关键词:路基;非饱和土;含水量;非稳态流;蓄洪
中图分类号:TG111.3 文献标志码:A 文章编号:1672-7207(2012)04-1514-05
Water content distribution in embankment subjected to floodwater
HE Wei, FU Hong-yuan, YAN Zhi-wei
(School of Civil & Architecture, Changsha University of Science & Technology, Changsha 410114, China)
Abstract: Based on the fact that the embankment in floodwater storage district will be influenced by flood frequently, the water content distribution in embankment subjected to floodwater was studied. The effect of circumstance in normal and flood storage period were analyzed firstly. Based on this, the Richards’ equation was introduced, and FEM format for relevant unsteady state flow of unsaturated soil was deduced by Galerkin’s weighted residual method, and the normal head pressure condition was taken into account by Dirichlet’s theory. Then, the Fredlund’s model of soil water characteristic curve for unsaturated soil, as well as the method to estimate the unsaturated premeability coefficient were introduced to analyze the real soil, and the calculation parameters were obtained. Lastly, the method was applied to analyze embankment subjected to floodwater, and the pore water pressure and water content distributions were obtained. The results indicate that flow in embankment subjected to floodwater can soon reach steady state, and embankment slope unstability caused by water content change should be considered in engineering practice.
Key words: embankment; unsaturated soil; water content; unsteady state flow; floodwater storage
随着国家西部大开发战略、中部崛起战略的实施和交通事业的飞速发展,交通路线经常经过湖区洪灾易发地段,为了使洪峰顺利通过,这些地区常借用河道周边区域蓄洪,起到缓冲的作用。如湖南省汉寿县省道S205津武线仓儿总渡口处有较大区域在洪涝季节预备作为蓄洪区,届时该区域的公路路基将受到洪水的浸泡。长时间受到洪水的浸泡可能引起2个问题:一是路基发生非饱和渗流,有渗流力作用于路基边坡;二是路基及其下地基浸水后抗剪强度降低。这2个因素均有可能降低路基的稳定性[1-2]。徐光明等[3]通过模拟短期雨水入渗及长期入渗条件对边坡进行了离心机试验,结果表明:长期入渗条件将使浅层土体强度显著降低,临界坡高明显减小。由此可见,研究蓄洪条件引起的路基边坡问题十分必要。由蓄洪条件引起的路基边坡问题是典型的非饱和土问题,对于工程采用土体含水量间接分析其特性是有效手段[4-5]。在此,本文作者拟采用非饱和土非稳态流分析方法对洪水浸泡条件下路基边坡及地基含水量变化规律进行研究。
1 蓄洪区环境对路基边坡的影响
蓄洪区路基边坡填筑完成后,路基填料均处于最佳含水量状态,在水头梯度的作用下,地下水位以上的路基与地基土各点孔隙水压力水头逐渐与地下水位平衡(如图1(a)所示)。在蒸腾作用的影响下,地表孔压进一步下降,为地下水逸出提供了源动力。通常,在正常使用期也有降雨发生,其雨水会以地表流量的形式渗入地表,超过地基土渗透系数的流量以地表径流的形式由路基排水系统排出,保持地表处水头为0[6]。
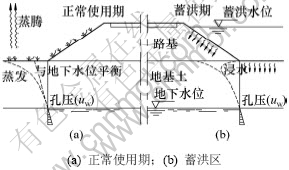
图1 蓄洪区路基边坡环境影响示意图
Fig.1 Schematic map of embankment in district storage floodwater
水头差是土体内部发生渗流的直接原因,若地表排水不畅,则可能引起地表处水头差不为0,且地基土较长时间处于地表渗入状态,对路基稳定性不利。而在蓄洪期,洪水的来临与消退往往经历较长时间,这意味着路基可能在汛期受到洪水的浸泡(如图1(b)所示)。在较长一段时间内,地表水头均大于0,这对路基稳定性很不利。由于地基土应力状态的改变,其含水量将发生变化[6],导致地基土变软,抗剪强度下降。可能影响地基土含水量变化规律的因素如下。
(1) 土体应力状态。土体单元所受的应力状态是导致含水量变化的根本原因,但对其进行分析十分困难。通常认为,土体单元上作用的基质吸力是引起含水量变化的主要因素[7]。
(2) 土水特征曲线的斜率。土水特征曲线在描述非饱和土工程性质起着非常重要的作用[8-10],土水特征曲线的斜率是将基质吸力与土体含水量联系起来的特征参数。
(3) 作用时间。对于非稳态流,作用时间是土体含水量变化的关键因素,但当渗流达到稳态条件后,土体含水量不再改变,与作用时间无关。
此外,水头差是引起非饱和土渗流的决定性因素,但对于土体含水量的改变,水头差并不是直接因素。例如,对于稳态流,水头差依然将引起土体渗流,但土体内部各点含水量保持不变。鉴于蓄洪区特点,本文着重探讨作用时间的影响。
2 基本方程与土性参数
2.1 控制微分方程
与非稳态流相比,稳态流符合达西定律,与饱和土理论一致,所不同的是土体渗透系数除与孔隙比、土体级配有关之外,还受到土体中基质吸力的影响[5]。而对于非稳态流,应力状态(基质吸力为主要因素)会改变土体含水量,土体中渗流状态会随着时间发生改变。目前,对土体非稳态流的研究多基于经典的Richards方程进行。二维非饱和土单元的控制方程 为[8]:
 (1)
(1)
式中:h为总水头;kx为x方向土体渗透系数;ky为y方向土体渗透系数;mw为土水特征曲线斜率;γw为水的重度。
其有限元格式可根据Galerkin加权残量原理,由三角形单元的面积和边界表面积分得到,其表达式为:
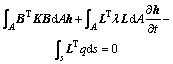 (2)
(2)
式中:A为土体单元面积;B为面积坐标的导数矩阵,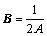
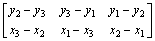 ;K为单元内土体渗透系数张量,
;K为单元内土体渗透系数张量, ;h为作用在单元各节
;h为作用在单元各节
点上的总水头,h=[h1 h2 h3]T;λ=mwγw,mw在某一时间段可认为是常数;L为单元内各点面积坐标,q为单元外部垂直于单元边界方向的水流速率;s为单元周长。
L=[L1 L2 L3];
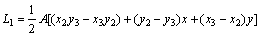 ;
;
 ;
;
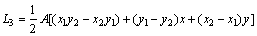 。
。
结合Dirichlet条件规定边界节点处水头,即得到可考虑洪水浸泡作用的非稳态渗流有限元解法。
2.2 土性参数分析方法
由式(1)可知:对非稳态渗流问题进行分析,需先确定土体的土水特征曲线及饱和-非饱和渗透系数曲线。国内外许多学者对其进行了研究,如:Pham等[9-11]提出土水特征曲线预测模型;Fredlund等[12]提出基于土水特征曲线的土体非饱和渗透系数预测方法,其预测模型可写为:
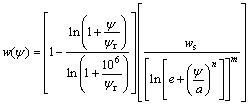 (3)
(3)
式中:w为非饱和土体含水量;ws饱和状态土体含水量;ψ为土体吸力;ψr为残余含水量对应的土体吸力;a,n和m为土水特征曲线的形状系数,其中,a与土体进气点有关,n和m与土水特征曲线斜率有关。以文献[13]中的土水特征曲线实测数据为例,用上述方法进行分析,结果如图2所示。
由图2可得拟合相关系数为0.97,由此可知:Fredlund, Xing模型用于预测水土特征曲线效果较好,但由实测曲线后段与拟合曲线的后段下降趋势稍有不同。可见:要使计算结果精确,样本范围需要覆盖整个可能发生的吸力区间。

图2 水土特征曲线拟合曲线
Fig.2 Fitting curve and measured SWCC
基于土水特征曲线与Mualem提出的预测理论,Fredlund等[11]建立了预测非饱和土渗透系数方程:
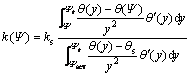 (4)
(4)
式中:ks为饱和时土的渗透系数;y为积分变量,对应于图3中的横坐标;Ψaev为土体进气点吸力;θ′(y)为水土特征曲线的导数,其物理意义为图3所示的水土特征曲线的斜率。
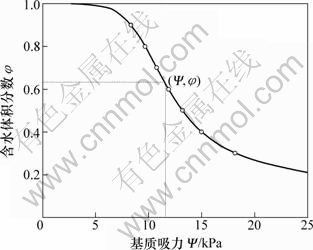
图3 水土特征曲线
Fig.3 Soil-water characteristic curve
大量研究表明,该模型可较好地反映非饱和土渗透特性。由于文献[14]并未给出相应渗透系数实测值,本文未对该模型进行验证。
3 路基含水量变化规律的有限元 分析
取路基尺寸如图4所示。假定蓄洪水位与路基顶面一致,采用文献[12]中所述土类进行分析,饱和时渗透系数取10-7 cm/s[15],结合Fredlund非饱和渗透系数预测方法及文献[13]中计算结果综合确定非饱和渗透曲线。
采用本文所述有限元方法分析蓄洪条件下公路路基含水量随蓄洪时间的变化规律,计算结果如图5和图6所示。未蓄洪前假定路基达到稳定状态,由于在稳定状态路基中无渗流发生,因此,截面各点总水头相等,土体孔压为负值。而蓄洪时,土体表面受到常水头作用,水在边坡内部发生非稳态渗流,改变土体内部孔压分布与含水量分布。由图5与图6可知:蓄洪条件下土体含水量的影响深度可达3~4 m,但对深部土体基本无影响。
提取距边坡坡顶3 m处截面数据,得孔压与土体饱和度随深度与蓄洪时间的变化关系如图7与图8所示。由图7与图8可知:蓄洪期达到稳定后计算截面地表总水头为原负孔压水头加洪水引起的水头,蓄洪时间为40 d与90 d时孔压及饱和度基本相同,说明蓄洪时间不用太长,路基边坡即可达到稳态流状态;此外,孔压先高于原稳定态孔压线,在深度2~4 m之间与稳定态孔压线相比略低。这是由于边坡表面的常水头分布改变了边坡表层孔压原有的分布形式,使边坡沿坡面方向一定深度范围内孔压略减小,如图5(b)所示。

图4 蓄洪条件下路基分析模型示
Fig.4 Sketch map of embankment when storaging floodwater

图5 路基边坡孔压分布图
Fig.5 Pore-water pressure distribution in embankment

图6 路基边坡体积含水量分布
Fig.6 Water content distribution in embankment
从图8可见:表层土饱和度改变不大,但这一改变量与表层孔压有关,越靠近边坡坡趾的点表层土饱和度越大,该例中坡址表层土已达到最大饱和度;越靠近边坡下部,土体的软化效应越明显,这对边坡稳定性十分不利。而浅层地基受到洪水浸泡作用含水量变化较大,亦有可能发生浅层滑动。因此,洪水消退后需注意防止边坡的整体与浅层滑动。
本文未考虑正常使用期的蒸腾作用影响,因此,初始状态的孔压场略高,若计入其影响,蓄洪对边坡及地基含水量的影响将增大,有必要对其进行进一步研究。
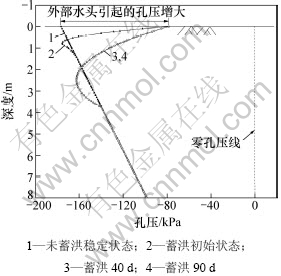
图7 计算截面孔压随蓄洪时间的变化
Fig.7 Variation of pore water pressure with time
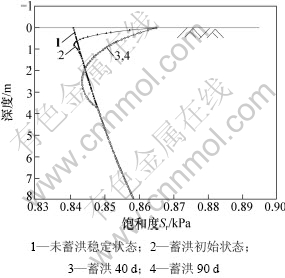
图8 计算截面饱和度随蓄洪时间的变化
Fig.8 Variation of saturated degree with time
4 结论
(1) 蓄洪条件下路基边坡可在较短的时间(40 d之内)基本达到稳态流条件,这意味着边坡含水量的改变将在较短时间内完成。因此,在蓄洪区路基边坡设计时,不应认为汛期较短而不考虑浸水的影响。
(2) 蓄洪条件下路基表层以下3~4 m含水量变化较明显,洪水消退后应注意防止边坡的浅层滑动。
(3) 边坡表层土的最终饱和度与其所处的位置有关,位置越低,最终饱和度越大,这不利于边坡整体稳定。
参考文献:
[1] Collins B D, Dobroslav Znidarcic. Stability analysis of rainfall induced landslides[J]. Journal of Geotechnical Engineering, ASCE, 2004, 130(4): 362-272.
[2] Schmertmann J H. Estimating slope stability reduction due to rain infiltration mounding[J]. Journal of Geotechnical Engineering, ASCE, 2006, 132(9): 1219-1228.
[3] 徐光明, 王国利, 顾行文. 雨水入渗与膨胀性边坡稳定性试验研究[J]. 岩土工程学报, 2006, 28(2): 270-273.
XU Guang-ming, WANG Guo-li, GU Xing-wen. Centrifuge modeling for instability of excavated slope in expansive soil due to water infiltration[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 270-273.
[4] 沈珠江. 非饱和土力学实用化之路探索[J]. 岩土工程学报, 2006, 28(2): 256-259.
SHEN Zhu-jiang. Exploitation of practical use of unsaturated soil mechanics[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 256-259.
[5] 贺炜, 陈永贵, 王泓华. 基于正态分布的土水特征曲线独立域滞后模型研究[J]. 长沙理工大学学报: 自然科学版, 2009, 6(2): 28-32.
HE Wei, CHEN Yong-gui, WANG Hong-hua. Independent domain hysteretic model for SWCC by introducing normal distribution function[J]. Journal of Changsha University of Science & Technology: Natural Science, 2009, 6(2): 28-32.
[6] Charles W W Ng, Pang Y W. Influence of stress state on Soil-Water characteristics and slope stability[J]. Journal of Geotechnical Engineering, ASCE, 2000, 126(2): 157-166.
[7] Fredlund D.G., Rahardjo H. Soil mechanics for unsaturated soils[M]. New York: John Wiley & Sons, 1993: 1-20.
[8] Lam L, Fredlund D G, Barbour S L. Transient seepage model for saturated-unsaturated soil systems: A geotechnical engineering approach[J]. Canadian Geotechnical Journal, 1987, 24(4), 565-580.
[9] Pham H Q, Fredlund D G, Barbour S L. A Study of hysteresis models for soil-water characteristic curves[J]. Canadian Geotechnical Journal, 2005, 42(6): 1548-1568.
[10] Nimmo J R. Semi-empirical model of soil water hysteresis[J]. Soil Science Society of American Journal, 1992, 56: 1723-1730.
[11] Fredlund D G, Xing A. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532.
[12] Fredlund D G, Xing A, Huang S Y. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve”[J]. Canadian Geotechnical Journal, 1994, 31(4): 533-546.
[13] 叶为民, 钱丽鑫, 白云. 由土-水特征曲线预测上海非饱和软土渗透系数[J]. 岩土工程学报, 2005, 27(11): 1262-1265.
YE Wei-min, QIAN Li-xin, BAI Yun. Predicting coefficient of permeability from soil-water characteristic curve for Shanghai soft soil[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1262-1265.
[14] 叶为民, 白云, 金麒. 上海软土土水特征的室内试验研究[J]. 岩土工程学报, 2006, 28(2): 260-263.
YE Wei-min, BAI Yun, JIN Qi. Lab experimental study on soil-water characteristics of Shanghai soft clay[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 260-263.
[15] 钱家欢, 殷宗泽. 土工原理与计算[M]. 2版. 北京: 中国水利水电出版社, 1995: 109-111.
QIAN Jia-huan, YIN Zong-ze. Principal and calculation of soil mechanics[M]. 2nd ed. Beijing: China Waterpower Press, 1995: 109-111.
(编辑 陈灿华)
收稿日期:2011-05-27;修回日期:2011-08-10
基金项目:国家自然科学基金资助项目(50908024);西部交通建设科技项目(2009318000048);湖南省交通科技项目(200904)
通信作者:贺炜(1982-),男,湖南株洲人,博士,副教授,从事岩土工程防灾减灾、非饱和土理论与应用、深基础工程研究;电话:0731-85258698;E-mail:heweicslg@yahoo.com.cn