DOI: 10.11817/j.issn.1672-7207.2020.02.025
能源桩全生命周期热响应半径简化计算方法
王哲1,刘耶军1,张正威2,翁凯文1,郑秀玲2,许四法1
(1. 浙江工业大学 建筑工程学院,浙江 杭州,310014;
2. 浙江农林大学 风景园林与建筑学院,浙江 杭州,311300)
摘要:根据工程中群桩埋管换热器状况,采用叠加原理计算群桩埋管的桩壁温度,定义能源桩埋管换热器的热响应半径为周围其他桩引起的过余温度影响系数≤5%时相邻桩中心线之间的垂直距离;在大量计算分析的基础上,采用最小二乘法拟合出单工况荷载作用下能源桩埋管换热器热响应半径计算公式;考虑到实际能源桩工程系统运行时每延米换热功率是关于时间的函数,建立动态负荷作用下能源桩三维传热数值模型,分析不同荷载分布形式、峰值负荷、运行时间以及全生命周期对能源桩热响应半径的影响。研究结果表明:在单桩、单排桩、双排桩和多排桩布置状况下,本文拟合公式的热响应半径计算结果与无限长线热源模型解析解之间的最大相对误差分别为4.62%,4.45%,3.77%和3.32%,说明该方法具有较高的计算精度,符合工程要求;荷载分布形式以及峰值负荷仅影响桩周岩土体中过余温度及其梯度,桩周岩土体热扩散系数及运行时间影响温度传递范围;根据工程中最常见的多排桩布置方式,得到不同桩径和不同岩土体热扩散系数条件下能源桩热响应半径随时间的变化关系,可为工程应用提供参考。
关键词:热响应半径;计算模型;能源桩;数值模拟;传热特性
中图分类号:U443.15 文献标志码:A
文章编号:1672-7207(2020)02-0514-09
Simplified calculation method of thermal response radius of energy pile in its whole life cycle
WANG Zhe1, LIU Yejun1, ZHANG Zhengwei2, WENG Kaiwen1, ZHENG Xiuling2, XU Sifa1
(1. School of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China;
2. School of Landscape Architecture, Zhejiang Agriculture and Forestry University, Hangzhou 311300, China)
Abstract: According to the condition of pile-group buried heat exchanger in engineering, the temperature of pile-group buried heat exchanger was calculated by superposition principle, and the thermal response radius of pile-based buried heat exchanger was defined as the vertical distance between center lines of adjacent piles when the excess temperature influence coefficient caused by other piles was less than or egual to 5%. On the basis of a large number of calculation and analysis, the calculation formula for thermal response radius of energy pile buried heat exchanger was fitted using the least squares method under working condition of single load response. In view of the actual energy pile, per linear meter heat power of engineering system in running time was a function of time, energy piles three-dimensional heat transfer numerical model was set up under the action of dynamic load, and the the influences of different load distribution forms, peak load, running time and the whole life cycle on the thermal response radius of energy pile were analyzed. The results show that in cases of single pile, single row, double row piles and pile arrangement, the maximum relative error between thermal response radii obtained from the proposed formula and analytical solution of infinite long heat source model are 4.62%, 4.45%, 3.77% and 3.32%, respectively. The method has higher accuracy and can meet the demands of engineering. The load distribution form and size of the peak load only affect the excess temperature and gradient in the surrounding rock mass, while pile rock and soil body heat diffusion coefficient and temperature area are influenced by operation time. According to the most common arrangement of multi-row piles in practice, the relationship between thermal response radius of energy piles with time under different pile diameters and different thermal diffusivity of rock-soil mass is plotted, which provides reference for the engineering application.
Key words: thermal response radius; calculation model; energy pile; numerical simulation; heat transfer characteristics
随着能源压力的增加,能源桩技术迅速发展。能源桩是将热交换管预先埋置在建筑桩基础中,并通过管内循环流体与浅层地热能进行热交换。与传统的地源热泵技术相比,具有占地空间小、不需要额外的钻孔费用等优点,因而,在实际工程中逐渐得到广泛应用。鉴于传统能源桩传热特性问题,国内外学者提出了多种地下换热器传热解析模型[1-6],然而,如何根据现场地质条件确定能源桩埋管换热器间距一直是困扰工程师的主要问题之一。目前,有关能源桩埋管换热器热响应半径的研究较少,且考虑到我国幅员辽阔,不同热工分区的岩土体热物性参数、系统规模程度和使用方式也会有较大差异,因此,常常给工程设计带来非常大的不确定性。国内外关于地下换热器布置间距取值的相关规范也很不相同,例如瑞典为10 m,奥地利为2.5 m[7],中国“地源热泵系统工程技术规范”[8]中布置间距取值为3~6 m,但都没有给出相应的计算方法。HART等[9]在研究单孔埋管地下换热器传热特性时,根据远场边界处岩土体温度等于初始温度这一条件计算出远场边界热响应半径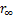 。对于工程中常用的群管换热器,因为岩土体温度随着远离热源呈指数衰减,所以,根据
。对于工程中常用的群管换热器,因为岩土体温度随着远离热源呈指数衰减,所以,根据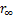 布置来安排钻孔将会浪费大量的场地。SIGNORELLI等[10]通过算例计算得出竖直埋管地下换热器热响应半径约为15 m。王艳等[11]采用数值仿真软件对竖直埋管换热器热响应半径的影响因素进行了模拟分析,但也没给出相应的结论或计算方法。王美燕等[12]提出了一种运用量纲—参数曲线的竖直埋管换热器热响应半径计算方法,但该方法要对建筑物冷热负荷平衡问题进行研究,对工程应用有一定的难度。李晓星等[13]提出了一种地源热泵地下换热器热响应半径计算方法,但所研究的钻孔孔径在100~200 mm之间,不太适合计算大孔径能源桩埋管换热器的热响应半径。张正威等[14]在不考虑钻孔孔径影响的基础上提出了地源热泵埋管换热器热响应半径简化计算方法,该方法考虑了岩土体的热物性参数、地源热泵系统的运行时间以及现场钻孔布置方式等的影响,但也仅适用于传统地源热泵系统的运行方式。综上所述,人们对现有的能源桩埋管换热器热响应半径研究较少,缺乏实际的工程应用依据,大多局限在地源热泵竖直埋管换热器热响应半径的研究。赵石娆等[15]的研究表明,竖直埋管换热器的轴向长度比径向长度差几个数量级,现有传热解析模型在能源桩和地源热泵系统使用时间内温度场计算结果没有明显差异。为此,本文作者采用比较简单的无限长线热源传热解析模型,在不考虑热—力相互耦合作用下[16-18],分析桩周岩土体过余温度场的分布特征,在大量计算和分析的基础上,利用最小二乘法拟合出单工况荷载作用下能源桩热响应半径计算公式。通过数值模拟方法研究变负荷作用对能源桩热响应半径的影响,并提出能源桩全生命周期热响应半径简化计算方法。
布置来安排钻孔将会浪费大量的场地。SIGNORELLI等[10]通过算例计算得出竖直埋管地下换热器热响应半径约为15 m。王艳等[11]采用数值仿真软件对竖直埋管换热器热响应半径的影响因素进行了模拟分析,但也没给出相应的结论或计算方法。王美燕等[12]提出了一种运用量纲—参数曲线的竖直埋管换热器热响应半径计算方法,但该方法要对建筑物冷热负荷平衡问题进行研究,对工程应用有一定的难度。李晓星等[13]提出了一种地源热泵地下换热器热响应半径计算方法,但所研究的钻孔孔径在100~200 mm之间,不太适合计算大孔径能源桩埋管换热器的热响应半径。张正威等[14]在不考虑钻孔孔径影响的基础上提出了地源热泵埋管换热器热响应半径简化计算方法,该方法考虑了岩土体的热物性参数、地源热泵系统的运行时间以及现场钻孔布置方式等的影响,但也仅适用于传统地源热泵系统的运行方式。综上所述,人们对现有的能源桩埋管换热器热响应半径研究较少,缺乏实际的工程应用依据,大多局限在地源热泵竖直埋管换热器热响应半径的研究。赵石娆等[15]的研究表明,竖直埋管换热器的轴向长度比径向长度差几个数量级,现有传热解析模型在能源桩和地源热泵系统使用时间内温度场计算结果没有明显差异。为此,本文作者采用比较简单的无限长线热源传热解析模型,在不考虑热—力相互耦合作用下[16-18],分析桩周岩土体过余温度场的分布特征,在大量计算和分析的基础上,利用最小二乘法拟合出单工况荷载作用下能源桩热响应半径计算公式。通过数值模拟方法研究变负荷作用对能源桩热响应半径的影响,并提出能源桩全生命周期热响应半径简化计算方法。
1 长时间作用下能源桩传热特性
国内外许多学者对竖直埋管地下换热器的传热特性进行了研究,并提出了多种传热解析模型,一般可分为线热源模型、面热源模型和体热源模型。假设地下岩土的导热系数为1.2 W/(m·K),热扩散系数为10-6 m2/s,能源桩每延米放热功率为50 W/m,桩径为0.6 m,桩长为30 m。图1所示为不同解析模型桩壁处过余温度随时间的变化。从图1可以看出:长时间作用下几种代表性解析模型的计算结果差异很小。为此,本文采用相对简单的无限长线热源模型[1]:
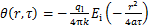 (1)
(1)
式中: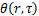 为过余温度,
为过余温度,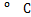 ;
;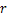 为圆柱坐标系中的径向坐标,
为圆柱坐标系中的径向坐标,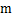 ;
;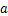 为地下岩土体的热扩散系数,
为地下岩土体的热扩散系数,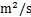 ;
;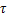 为时间,
为时间,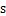 ;
;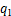 为每延米换热功率,
为每延米换热功率,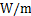 ;
;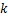 为岩土体的导热系数,
为岩土体的导热系数,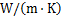 ;
;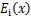 为指数积分函数。
为指数积分函数。
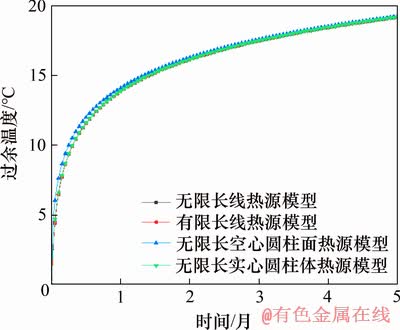
图1 不同解析模型中过余温度计算结果对比
Fig. 1 Comparison of excess temperature calculation results of different analytical models
图2所示为不同计算时间下能源桩桩周岩土体过余温度的径向分布图。从图2可以看出:桩壁的过余温度是最大的,并且远离桩壁呈指数衰减;随着时间的增加,过余温度持续传递到周围的岩土体中,过余温度逐渐增加,热响应半径也随之增大。
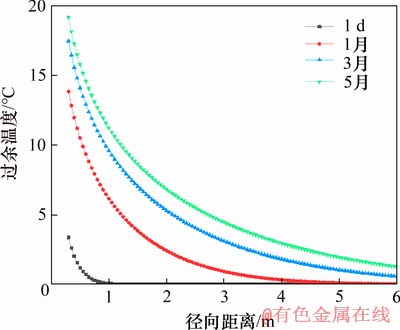
图2 过余温度沿径向分布
Fig. 2 Excess temperature distribution in radial direction
2 单工况荷载作用下热响应半径
2.1 群桩埋管换热器桩壁过余温度计算
在实际能源桩系统工程中,能源桩埋管换热器通常由多个桩组成,布置方式主要有3种类型:单排桩、双排桩、多排桩(3排及3排以上)等间距布置。在多排布置方式下,桩编号为1,2,3,…,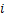 ,…,
,…,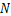 。
。
地下岩土体假定为均匀、各向同性材料,热传导过程在均匀介质中是线性的,根据叠加原理,编号为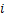 的桩桩壁过余温度可按下式计算[13]:
的桩桩壁过余温度可按下式计算[13]:
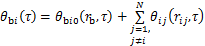
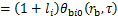
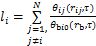 (2)
(2)
式中: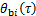 为第
为第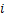 个桩桩壁过余温度,℃;
个桩桩壁过余温度,℃;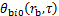 为第
为第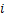 个桩自身引起的桩壁过余温度,℃;
个桩自身引起的桩壁过余温度,℃;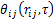 为第
为第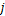 个桩引起的第
个桩引起的第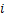 个桩桩壁附加过余温度,℃;
个桩桩壁附加过余温度,℃;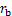 为桩半径,
为桩半径,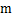 ;
;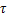 为时间,
为时间,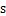 ;
;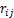 为第
为第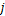 个桩至第
个桩至第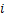 个桩的距离,
个桩的距离,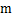 ;
;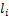 为第
为第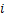 个桩周围其他桩对第
个桩周围其他桩对第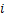 个桩的过余温度影响系数。
个桩的过余温度影响系数。
2.2 热响应半径定义
埋在地下岩土层中的能源桩埋管换热器会对整个岩土层的温度产生影响。对于单个能源桩,所产生的岩土体过余温度随离桩壁距离的增加而呈指数衰减,当衰减至足够小且在能源桩设计中可以忽略不计时,其对应的距离便是能源桩埋管换热器的热响应半径。对于群桩埋管换热器,还需要考虑其他能源桩所引起的温度场的影响。在能源桩的整个系统运行时间内,当周围其他桩引起的过余温度影响系数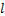 ≤5%时,工程上相邻桩之间的热干扰可以忽略不计,此时,相邻能源桩中心线之间的垂直距离便可作为能源桩埋管换热器的热响应半径。一般在距离计算桩2倍桩距外的其他桩对计算桩的附加过余温度影响系数很小,因此,对3排以上多排桩可按3排计算其热响应半径[13]。
≤5%时,工程上相邻桩之间的热干扰可以忽略不计,此时,相邻能源桩中心线之间的垂直距离便可作为能源桩埋管换热器的热响应半径。一般在距离计算桩2倍桩距外的其他桩对计算桩的附加过余温度影响系数很小,因此,对3排以上多排桩可按3排计算其热响应半径[13]。
2.3 热响应半径计算方法
参考文献[8],岩土热扩散系取0.5×10-6~1.6×10-6 m2/s,假设能源桩系统处于冷热负荷平衡状态,计算时间可按单一制冷或者制热工况取1~5月,桩基直径按工程常规取0.4~1.2 m。确定能源桩的热响应半径应该考虑岩土体内垂直于能源桩轴线方向的热响应最大区域,此时可忽略地表的影响。根据无限长线热源模型(见式(1)),分别计算不同桩径、不同岩土热扩散系数和不同运行时间下能源桩埋管换热器的热响应半径,见图3。经拟合得:
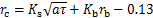 (3)
(3)
式中: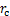 为热响应半径,
为热响应半径,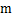 。
。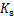 和
和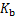 分别为岩土介质和桩半径修正系数,当桩为单桩时,
分别为岩土介质和桩半径修正系数,当桩为单桩时,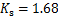 ,
,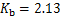 ;当桩单排布置时,
;当桩单排布置时,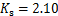 ,
,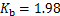 ;当桩双排布置时,
;当桩双排布置时,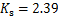 ,
,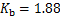 ;当桩多排布置时,
;当桩多排布置时,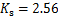 ,
,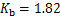 。
。
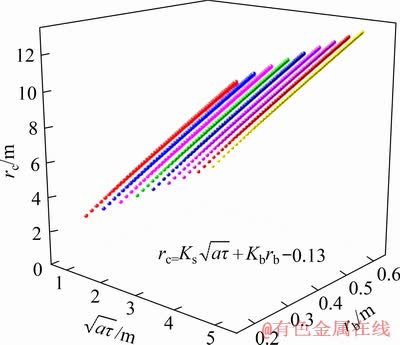
图3 不同条件下热响应半径
Fig. 3 Thermal response radii at different conditions
2.4 计算结果与分析
表1所示为单桩,单排桩、双排桩和多排桩布置状况下,拟合公式(3)中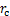 计算结果与式(1)解析解的对比。从表1可以看出,拟合公式的计算结果与解析解之间最大相对误差分别为4.62%,4.45%,3.77%和3.32%,结果表明拟合公式(3)具有较高的计算精度,符合工程要求。
计算结果与式(1)解析解的对比。从表1可以看出,拟合公式的计算结果与解析解之间最大相对误差分别为4.62%,4.45%,3.77%和3.32%,结果表明拟合公式(3)具有较高的计算精度,符合工程要求。
3 热响应半径影响因素分析
3.1 建筑负荷模型
本文利用浙江农林大学衣锦校区学术交流中心作为建筑模拟对象,该建筑南北朝向,建筑面积为418 m2,运用到能源桩系统的客房首层8间,二层5间,空调面积为162.79 m2,层高3.6 m。用DeST负荷软件来模拟夏热冬冷地区典型城市杭州1 a的逐时冷热负荷,建筑围护结构参数按照规范[19]所给出的不同热工分区限值来设置。杭州采暖运行期定于每年11月15日至次年3月15日,空调运行期为每年05-15—09-15。图4所示为杭州某建筑1 a逐时冷热负荷的模拟结果。
在进行动态负荷作用下能源桩系统设计时,根据建筑物冷热负荷峰值与所在地建议的能源桩每延米取放热量计算最大桩数;由DeST负荷软件模拟得出的建筑全年动态逐时冷热负荷和热泵机组的Ccop(制冷性能系数)和Hcop(制热性能系数)可计算出地下岩土体需要承受的逐时冷热负荷;将上述二者结合可以获得每个能源桩需要承担的逐时冷热负荷。
3.2 数值模型
由于现有解析模型假设热源每延米换热功率是恒定的,而实际工程项目中能源桩每延米换热功率是关于时间的函数,为了能准确研究动态负荷作用下的热响应半径,本文利用COMSOL Multiphysics有限元软件建立数值模型进行计算分析。
3.2.1 几何模型建立与材料属性赋予
单桩内建立1根U型管。U型管在桩中,桩和模拟范围内的岩土体可看成是圆柱体。模型的几何参数参考规范[8]给出的范围,U型管内径取25 mm,外径为32 mm,埋深为30 m,支管间距为180 mm,桩径为600 mm;岩土体模拟半径根据文献[13]中的模型的计算时间和岩土体的热扩散系数取6 m。U型管为聚乙烯管,管内的换热液为水,热物性参数如表2所示。
表1 热响应半径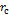 计算结果与式(1)解析解对比
计算结果与式(1)解析解对比
Table 1 Comparison of 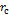 obtained from of the fitting formula and analytical solution of equation (1)
obtained from of the fitting formula and analytical solution of equation (1)
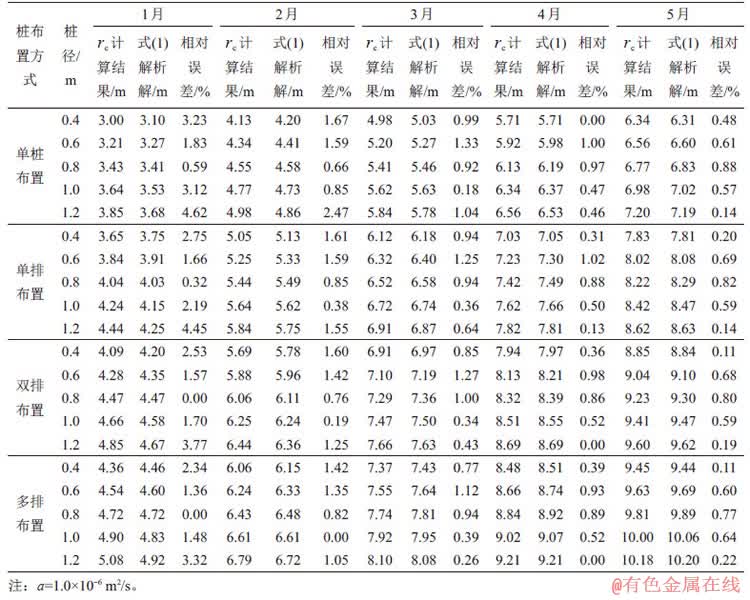
表2 热物性参数
Table 2 Thermophysical parameters
3.2.2 边界条件和初始条件
一般来说,地表以下5 m的岩土体温度全年基本不变,虽有波动,但这段距离占桩长的比例很小,因此,将岩土体最远边界处和底部设定为岩土体远边界恒温条件;岩土体表面暂不考虑外界四季温度变化所带来的影响,也设置为恒温边界条件;根据埋管内径,U型管入口流速设定为0.6 m/s。假定能源桩以每延米50 W/m的恒定功率放热;岩土体和管内水的初始温度为17.3 ℃。
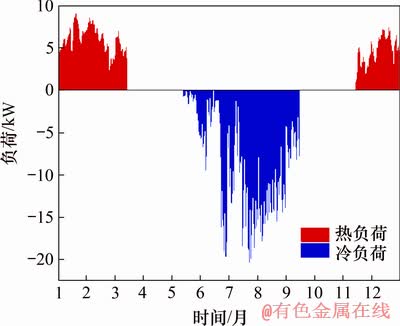
图4 杭州某建筑1 a逐时冷热负荷模拟结果
Fig. 4 Simulation results of hourly cooling and heating load of a building in Hangzhou during one year
3.2.3 网格划分与求解计算
网格划分时对U型管周围进行了详细划分,特别是在入口和出口处,岩土体由里到外网格密度由密到疏,网格划分如图5所示。划分网格时,选取3种不同网格单元数(138 855,252 751和572 249个)计算的过余温度相对误差在5%之内,满足精度要求,因此,选择第1种网格单元数进行划分以节约计算成本。使用时间步长为1 h的瞬态求解器求解模型。
3.2.4 模型验证
为了验证所建三维数值模型的正确性,对比无限长线热源传热解析模型,每延米放热功率统一取50 W/m,计算时间为3月,岩土体的热物性参数与表2中的保持一致。过余温度数值模型与解析模型计算结果对比如图6所示。由图6可知:过余温度数值模型的计算结果和解析模型趋势基本一致,验证了本文三维数值模型建立的正确性。
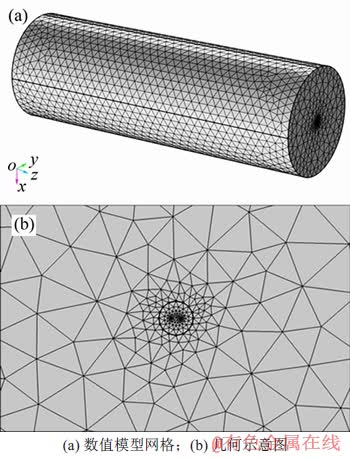
图5 数值模型网格与几何示意图
Fig. 5 Mesh and geometry diagrams of numerical model
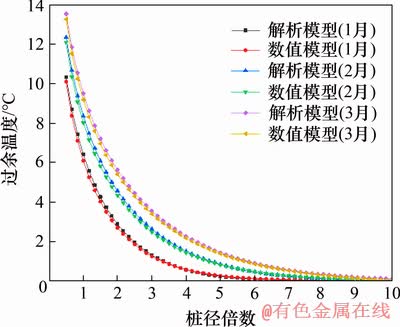
图6 数值模型与解析模型中过余温度计算结果对比
Fig. 6 Comparison of calculation results of excess temperature between the numerical model and the analytical model
3.3 影响因素分析
能源桩的运行工况往往是周期性的,在1个周期内存在制热运行期、制冷运行期以及间歇期,运行期内负荷随时间变化且存在1个峰值负荷,间歇期没有负荷作用。为此,本文分别研究不同荷载分布、不同峰值负荷、不同运行期以及全生命周期对热响应半径的影响。
3.3.1 荷载分布的影响
负荷采用3.1节中的计算结果。采用恒温法[20]计算得到杭州地区的能源桩每延米换热功率约为50 W/m;热泵机组的额定工况Hcop取4.5;制热工况运行时间为4月,从每年11月15日到次年的3月15日。随时间变化的负荷也可简化成矩形负荷,负荷峰一致,见图7。
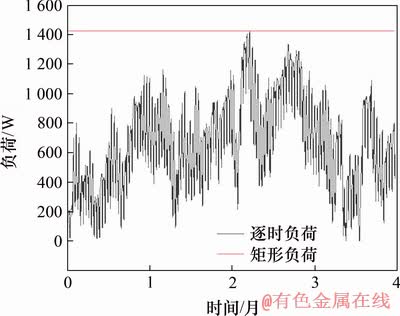
图7 不同荷载分布形式
Fig. 7 Different load distributions
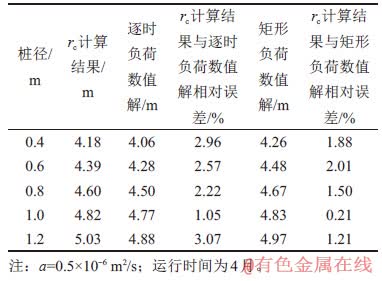
表3所示为运行时间为4月时热响应半径rc计算结果(见式(3))与2种荷载分布下rc数值解对比。从表3可以看出:由本文拟合公式所得rc计算结果与2种荷载下rc数值解的最大相对误差分别为3.07%和2.01%,表明相同作用时间内不同荷载分布的变化对热响应半径的影响较小,在实际工程中可将逐时负荷简化成矩形负荷来计算。
3.3.2 峰值负荷的影响
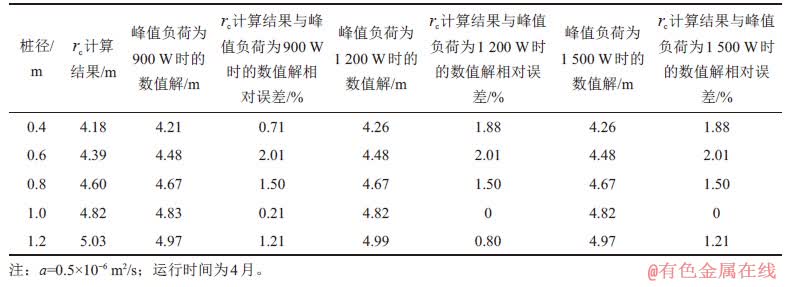
取峰值负荷分别为900,1 200和1 500 W,当运行时间为4月时本文rc计算结果(见式(3))与不同峰值负荷下数值解对比如表4所示。从表4可以看出:本文拟合公式rc计算结果与3种峰值负荷数值解的最大相对误差均为2.01%,表明不同峰值负荷对能源桩热响应半径影响很小。
表3 热响应半径计算结果与不同荷载分布下数值解对比
Table 3 Comparison of calculation results and numerical solutions of thermal response radius with different load distributions
3.3.3 运行期的影响
取运行期分别为3月、4月和5月,当峰值负荷为1 200 W时本文rc计算结果(见式(3))与不同运行期数值解对比如表5所示。从表5可以看出:拟合公式中rc计算结果与3种不同运行期数值解的最大相对误差分别为2.67%,2.01%和2.02%,表明运行期时间越长,能源桩热响应半径越大。
表4 热响应半径计算结果与不同峰值负荷下数值解对比
Table 4 Comparison of calculation results and numerical solutions of thermal response radius with different peak loads
3.3.4 全生命周期的影响
在能源桩埋管换热器实际运行中,通常是由加热和冷却2种过程组成的。假定荷载分布为矩形负荷,峰值负荷为1 500 W,制冷制热运行期为4月,间歇期为2月,运行30 a。
能源桩全生命周期内冷热负荷的总量可以相互抵消,计算时可取冷热负荷运行时最大热响应半径。在能源桩30 a运行周期内,桩壁处最大温升为11.62 ℃,最大热响应半径为4.76 m。在相同工况下,式(3)热响应半径计算结果为4.59 m,两者相对误差为3.57 %,表明在计算整个生命周期内的热响应半径时,拟合计算公式(3)仍具有较高的计算精度。
4 能源桩全生命周期热响应半径简化计算方法
为便于工程应用,取实际工程中应用最多的多排桩布置方式,计算时间为5月。分别计算不同桩径和不同岩土体热扩散系数条件下能源桩热响应半径随时间的变化关系,见图8。图中虚线表示的是“地源热泵系统工程技术规范”[8]中所推荐的钻孔间距范围。从图8可以看出:能源桩埋管换热器的热响应半径随着桩周岩土体热扩散系数的增大而增大,随系统运行时间的增加而增大,随能源桩桩径的增大而增大。从图8还可以看出:若能源桩在热扩散系数为0.5 10-6 m2/s的岩土体中运行时,按单一工况运行4月,能源桩热响应半径便超过了地源热泵规范所推荐的上限值。因此,在设计能源桩间距时,不能简单采取地源热泵规范所给的值,还需根据实际现场地质条件、运行时间以及桩径来选取。
10-6 m2/s的岩土体中运行时,按单一工况运行4月,能源桩热响应半径便超过了地源热泵规范所推荐的上限值。因此,在设计能源桩间距时,不能简单采取地源热泵规范所给的值,还需根据实际现场地质条件、运行时间以及桩径来选取。
表5 不同运行期热响应半径计算结果与数值解对比
Table 5 Comparison of calculation results and numerical solutions of thermal response radius at different operating periods
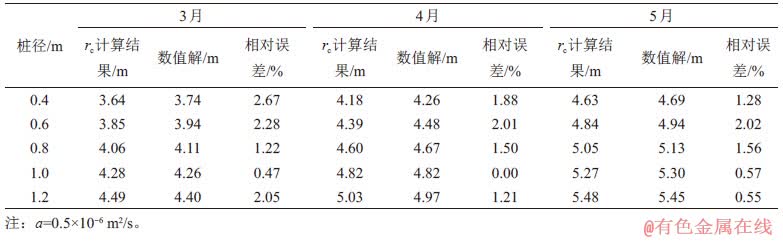
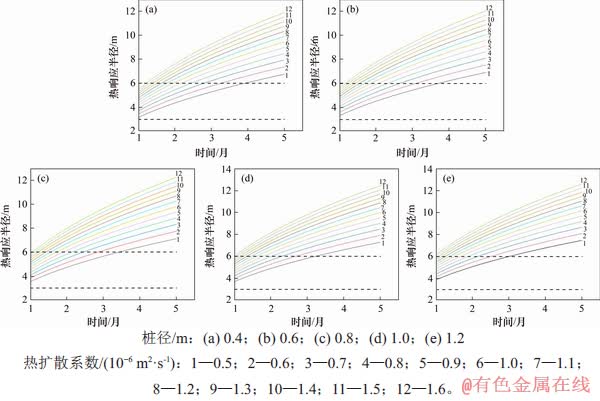
图8 能源桩不同桩径、不同热扩散系数下的热响应半径
Fig. 8 Thermal response radius of energy piles with different pile diameters and thermal diffusivities
5 结论
1) 岩土体中的过余温度在桩壁处最大,随着与桩壁距离的增加而迅速衰减,随时间的增加而增大。
2) 在单桩、单排桩、双排桩和多排桩布置情况下,本文拟合公式的热响应半径计算结果与无限长线热源模型解析解之间的最大相对误差分别为4.62%,4.45%,3.77%和3.32%,表明该方法具有较高的计算精度,符合工程要求。
3) 荷载分布形式以及峰值负荷只影响岩土体内过余温度及其梯度;岩土体热扩散系数及运行时间影响温度传递区域;全生命周期内冷热负荷的总量可以相互抵消,最大热响应半径计算可按单工况荷载作用下热响应半径计算方法。
4) 选取工程中应用最多的多排桩布置形式,绘制了不同桩径和不同岩土体热扩散系数条件下能源桩热响应半径随时间的变化关系,为工程应用提供参考。
参考文献:
[1] CARSLAW H S, JAEGER J C. Conduction of heat in solids[M]. Oxford,UK: Claremore Press, 1947, 78-88.
[2] INGERSOLL L R, PLASS H J. Theory of the ground pipe heat source for the heat pump[J]. Heating Piping and Air Conditioning, 1948, 6(1): 119-122.
[3] ZENG H Y, DIAO N R, FANG Z H. A finite line-source model for boreholes in geothermal heat exchangers[J]. Heat Transfer Asian Research, 2002, 31(7): 558-567.
[4] MEI V C, EMERSON C J. New approach for analysis of ground-coil design for applied heat pump systems[J]. ASHRAE Trans(United States), 1985, 91(2): 1216-1224.
[5] 张正威, 王美燕. 基于内外场合算的垂直埋管换热器传热模型[J].工程力学, 2014, 31(6): 269-274.
ZHANG Zhengwei, WANG Meiyan. Unified heat transfer model of vertical U-tube heat exchangers for ground source heat pump system[J]. Engineering Mechanics, 2014, 31(6): 269-274.
[6] 陈忠购, 张正威. 分层渗流地层中竖直地埋管的换热计算模型[J].太阳能学报, 2013, 34(5): 831-838.
CHEN Zhonggou, ZHANG Zhengwei. Analysis model for vertical borehole heat exchanger considering the layer-characteristics of soil and seepage[J]. Acta Energiae Solaris Sinica, 2013, 34(5): 831-838.
[7] HAEHNLEIN S, BAYER P, BLUM P. International legal status of the use of shallow geothermal energy[J]. Renewable and Sustainable Energy Reviews, 2010, 14: 2611-2625.
[8] GB 50366—2009. 地源热泵系统工程技术规范[S].
GB 50366—2009. Technical code for ground-source heat pump system[S].
[9] HART D P, COUVILLION R. Earth Coupled Heat Transfer[M]. Dublin, USA: Publication of the National Water Well Association, 1986: 35-48.
[10] SIGNORELLI S, KOHL T, RYBACH L. Sustainability of production from borehole heat exchanger fields[C]// Proceeding of the 29th Workshop on Geothermal Reservoir Engineering. California: Stanford University, 2004: 358-361.
[11] 王艳, 刁乃仁, 王京. U型管地热换热器热作用半径的数值模拟[J]. 建筑热能通风空调, 2011, 30(3): 46-49.
WANG Yan, DIAO Nairen, WANG Jing. Numerical simulation on thermal influencing radius of U-tube ground heat exchange[J]. Building Energy & Environment, 2011, 30(3): 46-49.
[12] 王美燕,张正威. 竖直地埋管换热器热作用半径的估算方法[J]. 浙江大学学报(工学版), 2013, 47(12): 2153-2159.
WANG Meiyan, ZHANG Zhengwei. Method for estimating thermal effect radius of vertical borehole heat exchangers[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(12): 2153-2159.
[13] 李晓星, 胡夏闽,张正威. 竖直埋管换热器热响应半径计算方法[J]. 农业工程学报, 2015, 31(17): 248-253.
LI Xiaoxing, HU Xiamin, ZHANG Zhengwei. The calculation method of the thermal response radius for vertical borehole heat exchangers[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(17): 248-253.
[14] 张正威, 赵石娆, 李晓星. 竖直埋管换热器热响应半径简化计算方法[J]. 太阳能学报, 2016, 37(9): 2338-2343.
ZHANG Zhengwei. ZHAO Shirao, LI Xiaoxing. The simplified calculation method of the thermal response radius for vertical borehole heat exchangers[J]. Acta Energiae Solaris Sinica, 2016, 37(9): 2338-2343.
[15] 赵石娆,张正威. 竖直地埋管换热器钻孔外换热解析模型研究现状[J]. 暖通空调, 2014, 44(1): 115-120.
ZHAO Shirao, ZHANG Zhengwei. A review of the analytical models for vertical borehole heat exchangers[J]. Journal of HV& AV, 2014, 44(1): 115-120.
[16] SENEVIRATNE H N, CARTER J P, AIREY D W, et al. A review of models for predicting the hermomechanical behavior of softclays[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(10): 715-733.
[17] ZOMMERMAN R W. Coupling in poroelasticity and thermoelasticity[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1): 79-87.
[18] BLOND E, SCHMITT N, HILD F. Response of saturated porous media to cyclic thermal loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(11): 883-904.
[19] GB 50189—2015. 公共建筑节能设计标准[S].
GB 50189—2015. Design standards for energy efficiency of public buildings[S].
[20] JGJ/T438—2018. 桩基地热能利用技术标准[S].
JGJ/T438—2018. Technical standard for utilization of geothermal energy through piles[S].
(编辑 伍锦花)
收稿日期: 2019 -05 -18; 修回日期: 2019 -07 -18
基金项目(Foundation item):国家自然科学基金资助项目(51778585) (Project(51778585) supported by the National Natural Science Foundation of China)
通信作者:许四法,博士,教授,从事基础工程和环境岩土工程等研究;E-mail: xusifa@zjut.edu.cn