J. Cent. South Univ. (2016) 23: 1740-1753

DOI: 10.1007/s11771-016-3228-4

Application of hybrid robust three-axis attitude control approach to overactuated spacecraft—A quaternion based model

A. H. Mazinan

Department of Control Engineering, Faculty of Electrical Engineering, South Tehran Branch,

Islamic Azad University (IAU), No. 209, North Iranshahr St., P.O. Box 11365/4435, Tehran, Iran

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: A novel hybrid robust three-axis attitude control approach, namely HRTAC, is considered along with the well-known developments in the area of space systems, since there is a consensus among the related experts that the new insights may be taken into account as decision points to outperform the available materials. It is to note that the traditional control approaches may generally be upgraded, as long as a number of modifications are made with respect to state-of-the-art, in order to propose high-precision outcomes. Regarding the investigated issues, the robust sliding mode finite-time control approach is first designed to handle three-axis angular rates in the inner control loop, which consists of the pulse width pulse frequency modulations in line with the control allocation scheme and the system dynamics. The main subject to employ these modulations that is realizing in association with the control allocation scheme is to be able to handle a class of overactuated systems, in particular. The proportional derivative based linear quadratic regulator approach is then designed to handle three-axis rotational angles in the outer control loop, which consists of the system kinematics that is correspondingly concentrated to deal with the quaternion based model. The utilization of the linear and its nonlinear terms, simultaneously, are taken into real consideration as the research motivation, while the performance results are of the significance as the improved version in comparison with the recent investigated outcomes. Subsequently, there is a stability analysis to verify and guarantee the closed loop system performance in coping with the whole of nominal referenced commands. At the end, the effectiveness of the approach considered here is highlighted in line with a number of potential recent benchmarks.

Key words: three-axis angular rates and rotations; sliding mode finite-time control approach; proportional derivative based linear quadratic regulator approach; dynamics and kinematics of overactuated spacecraft

1 Introduction

The attitude finite-time control scheme plays a significant role in the overall performance of the spacecraft. Up to now, the control approaches are improved, as long as a number of modifications can be made with respect to state-of-the-art. In the same way, the control scheme proposed here is realized based on a new hybrid control approach, which is now working in association with linear and nonlinear approaches. Based on the matter presented here, a PDLQR approach under optimum coefficients is employed to act as the linear control to deal with the quaternion vector, since a SMFC approach is also employed to act as the nonlinear control to deal with the whole of angular rates of the spacecraft. The present three-axis angular rates of the spacecraft is in fact first dealt with in the inner closed loop control, while the corresponding rotation angles in association with quaternion vector are then dealt with in the outer closed loop control. The inner closed loop of the proposed control approach is realized based on PWPF modulator to handle a number of on-off thrusters. In order to use an increased number of these on-off thrusters, CA technique is realized to provide overall performance of the spacecraft, in an accurate manner. The main idea behind the proposed approach is to deal with the quaternion vector to avoid presenting singularity of the rotation angles.

During the past decades, a number of efficient and applicable studies on the spacecraft attitude control have been carried out. JIN et al [1] proposed robust decentralized attitude coordination control of spacecraft formation, where BUSTAN et al [2] proposed in robust fault-tolerant tracking control design for spacecraft under control input saturation [1-2]. LU et al [3] proposed a design of control approach for rigid spacecraft attitude tracking with actuator saturation, since PUKDEBOON and ZINOBER [4] suggested an optimal sliding mode controllers for attitude tracking of spacecraft via Lyapunov function. MAZINAN et al [5] presented full quaternion based finite-time cascade attitude control approach via pulse modulation synthesis for a spacecraft. Moreover, Lyapunov-based three-axis attitude intelligence-based control approach with its application to unmanned aerial vehicle, spacecraft maneuvers control subject to propellant engine modes, three-axis detumbling mode control approach, high-precision full quaternion based finite-time cascade attitude control strategy and finally high-precision three-axis detumbling along with pointing attitude control strategy for a class of complicated space systems are a number of investigations presented by MAZINAN [6-10]. YEH [11] presented an approach to sliding-mode adaptive attitude controller design with its application to spacecrafts with thrusters, while JIN et al [12] suggested time-varying sliding mode attitude tracking control approach in rigid spacecraft. A self-tuning PID control approach to three-axis stabilization in the area of a spacecraft with unknown parameters was suggested by MORADI [13], while time-varying sliding mode controls in the area of rigid spacecraft attitude tracking was presented by JIN et al [14] and also adaptive sliding mode control with its application to six-DOF relative motion of spacecraft under input constraint was given by WU et al [15]. Furthermore, adaptive backstepping fault-tolerant control for flexible spacecraft under unknown bounded disturbances as well as actuator failures was presented by JIANG et al [16] and realization of attitude control of spacecraft was presented by BUTYRIN et al [17], as long as HU and ZHANG [18] suggested finite-time coordinated tracking control of spacecraft formation without velocity measurements.

FRESK and NIKOLAKOPOULOS [19] suggested full quaternion based attitude control for a quadrotor system. In this research, the closed loop control is designed based upon the quaternion, since its quaternion commands are dealt with, in an appropriate manner, to guarantee the control approach performance. SABATINI et al [20] proposed a method for delay compensation in the area of attitude control of flexible spacecraft. In this research, the strategy to compensate for delays is elaborated by means of a free floating platform, replicating the spacecraft attitude dynamics. The platform is equipped with thrusters through the on–off modulation of the linear quadratic regulator control law. A prediction of the state can be made through the mathematical model of the system in line with the rigid and elastic measurements enable, since the control is evaluated to make the predicted state relevant to a delayed time. ZHENG and SONG [21] suggested autonomous attitude coordinated control for a spacecraft. Three controllers including autonomous attitude coordinated control approach, a robust adaptive attitude coordinated control approach and finally a filtered robust adaptive attitude coordinated control approach are all realized to overcome the case in different situations of input constraints, model uncertainties, and external disturbances.

YANG et al [22] proposed nonlinear attitude tracking control for spacecraft.They have tried to deal with the attitude tracking control for spacecraft formation with communication delays. In this way, the sliding mode control in line with adaptive attitude synchronization control is realized. Afterwards, a non-smooth feedback function is used, since a class of nonlinear control approaches are designed for the attitude tracking of spacecraft. HUO et al [23] suggested finite-time fault tolerant attitude stabilization control for rigid spacecraft. In this work, a sliding mode control scheme is proposed to solve the problem of attitude stabilization for a rigid spacecraft. There is a precise reconstruction with zero observer error in finite-time, since the reconstructed information is acquired to synthesize a nonsingular terminal sliding mode attitude control approach together with the system states. In Ref. [24], an attitude synchronization control for a class of flexible spacecrafts is proposed to deal with the problem of attitude synchronization for a class of flexible spacecrafts. Using the backstepping realization in association with the neighbor-based design rule, a distributed attitude control law is suggested. It is shown that the attitude synchronization could asymptotically be achieved, while the induced vibrations are suppressed under the proposed control law, simultaneously.

SONG et al [25] realized finite-time control for nonlinear spacecraft attitude via terminal sliding mode approach. In their research, a terminal sliding mode control approach with double closed loops is suggested to deal with spacecraft attitude control problem. These laws are included in the inner and the outer closed loops control. The strategy is proposed by using Lyaponov’s concept to ensure the occurrence of the finite-time sliding motion. LU and XIA [26] dealt with an adaptive attitude tracking control for rigid spacecraft with finite-time convergence. In this research work, the attitude tracking control problem with finite-time is addressed for rigid spacecraft with external disturbances and inertia uncertainties. As reported there, a fast nonsingular terminal sliding mode surface is designed without any constraint. The proposed control laws is organized in line with an adaptive control architecture, as chattering-free. YANG et al [27] reviewed spacecraft attitude determination and control using quaternion based methods. In this review, the present quaternion based methods are first discussed for spacecraft attitude determination and control. In the mentioned control system, some reduced quaternion models using vector component of the quaternion in the state space models are considered. Afterwards, some methods with the features including analytic solution of the LQR and also the reduced disturbance effect with stable nonlinear spacecraft system were presented. ZOU and KUMAR [28] presented an adaptive fuzzy fault-tolerant attitude control of spacecraft. They investigate the attitude control of spacecraft, since unknown mass moment of inertia matrix, external disturbances, actuator failures, and input constraints are all existed. In this presentation, a robust adaptive control approach is proposed via fuzzy logic in association with backstepping approach. There is a unit quaternion to describe the attitude of spacecraft for global representation. It should be noted that the uncertainty can be estimated through a fuzzy logic system, while an adaptive mechanism is derived. There are a number of quaternion feedback control laws to be applied to spacecraft. In order to present this literature’s survey in the concise form, the proceeding investigated results are all given briefly. MOUSAVI et al [29] presented a setup of hardware-in-the-loop in the area of attitude control through cold gas thrusters, while WIE and BARBA [30] presented a new method in quaternion feedback with its application to spacecraft with large angle maneuvers. HU et al [31] realized robust attitude control for spacecraft under assigned velocity and control constraints, while CAI and HUANG [32] dealt with the leader-following attitude control of multiple rigid spacecraft systems. Hereinafter, KUO and WU [33] presented in the area of attitude dynamics and control of miniature spacecraft via pseudo-wheels, once ZHANG et al [34] gave the attitude control of rigid spacecraft with disturbance generated by time varying exo-systems.

Regarding the control allocation research, JOHANSEN et al [35] presented a survey to address this issue. With this purpose, the subject of control allocation suggests the advantage of a modular design, as long as the high-level motion control algorithm is designed, since there are no detailed knowledge about the effectors and actuators. The objective of their research is to survey control allocation approaches, which are motivated by the wide range of applications that have expanded in the aerospace and maritime industries [35]. ZACCARIAN [36] has proposed dynamic allocation for input redundant control systems. It is proposed to address control systems under redundant actuators, where the concepts of weak and strong input redundancy are characterized. Based on the matter reported there, a dynamic augmentation is given to a control scheme which performs the plant input allocation. The proposed approach is developed for redundant plants and extended to the case of magnitude saturation and rate saturation. SERVIDIA [37] dealt with control allocation for gimbaled/fixed thrusters. There are some overactuated control systems, which are using a control distribution law between the controller and the actuators. The configuration of actuators are designed to operate after a single point of failure, for system optimization and decentralization objectives. In this research, the thruster configuration is realized in the fixed, single-gimbal and finally double-gimbal thruster cases. It is shown that the minimum number of thrusters could be obtained, since a specific control allocation is offered via a nonlinear programming approach [37-40]. As are obvious, the whole of above-referenced research in association with other related ones are all tried to address some efficient methods to deal with this complicated system. In the same way, the proposed control approach has now made another new effort, while its main differences w. r. t. these methods are given in the approach’s structure and the corresponding results. It can be noted that the motivation of the present article is to realize a hybrid control approach through linear and nonlinear terms realization, in a simultaneous manner, as long as the investigated outcomes are noticeably improved the recent results in the area of overactuated spacecraft modeling and control.

2 Proposed HRTAC approach

The schematic diagram of the proposed HRTAC approach is first illustrated in Fig. 1. The control method is organized based upon two closed loops including the inner and the outer closed loops. The responsibility of the inner loop is to deal with ω_μ; μ=x, y, z, while the responsibility of the outer closed loop is to deal with q_s. Due to the fact that the measurement of the angular rates, in a real application, are somehow faster than the quaternion vector or the angular rotations, the control performance is reasonably upgraded and guaranteed with respect to the corresponding traditional single closed loop systems. As are obvious here, the inner loop consists of 1) SMFC approach, 2) PWPF modulator, 3) CA scheme and finally 4) dynamics of the spacecraft. Hereinafter, the outer closed loop consists of the 1) PDLQR approach and 2) kinematics of the spacecraft, which is obviously organized in line with the quaternion equations. In this approach, the q_ref is dealt with in the proposed HRTAC approach, as the referenced input commends, since the q_s is the controlled quaternion vector output. In fact, the approach proposed here is a full quaternion based attitude control scheme, which has to be realized in association with the Euler angles to the quaternion vector converter sub-system and also the quaternion vector to the Euler angles converter sub-system, in order to deal with the rotational angles, in a constructive manner, by generating q_ref as the translated input commands. In the same way, the q_s is converted to the tracked Euler angles as the control system output. Both converter sub-systems are now obscured, for simplicity, in the below schematic diagram.

Fig. 1 Schematic diagram of proposed HRTAC approach

2.1 Spacecraft model

2.1.1 Attitude dynamic equation

The attitude dynamic equation is organized based on the following torque formula:

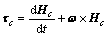                           (1)

Now, by addressing the three-axis angular rates, the three-axis control torque s of the spacecraft are realized as

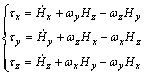                     (2)

By addressing three-axis angular momentum and moments of inertial in μ direction, the attitude dynamic equations are easily resulted by

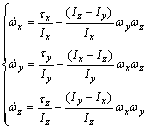                     (3)

Finally, by assuming “×” as cross product, the results can briefly be presented as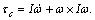

2.1.2 Attitude kinematics equation

The spacecraft model can be represented through the attitude kinematic and dynamics equations. Regarding the first one equation, it is now given using various attitude parameters such as Rodrigues, Euler angles, quaternion and others, since the representation via quaternion is more applicable. It should be noted that the quaternion is truly able to deal with non-singularity, while it is free from the trigonometric component. All in all, this representation is taken into consideration, as an appropriate candidate, to present the attitude behavior of a spacecraft. With this purpose, the q_s can first be presented in details as

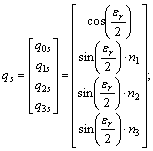
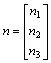            (4)

where q_is (i=1, 2, 3, 4) has the real and three imaginary elements and also the conditions ||q_s||=1 must be satisfied. Now, the relations between ω_x, ω_y, ω_z and the q_is can be presented by

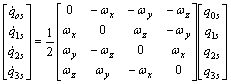         (5)

And the relations between f, θ, ψ and the q_is are now also given by

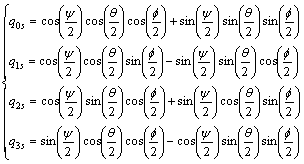 (6)

where the Euler angles can easily be calculated as

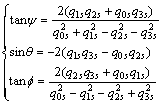                   (7)

2.2 Hybrid control scheme realization in line with PWPF and CA

2.2.1 PWPF realization

Various modulation methods have been used to relate the level of required torque, the width and the frequency of pulses via the PMS, due to the fact that reaction control approaches do not possess the linear relationship between the input to the control approach and its output torque. To shape the nonlinear output of on-off thrusters into linear request output, a number of thruster control methods can be exploited. The most frequently used method is now known as PWPF modulator. Others like Schmitt trigger control, pseudo rate modulator, integrated pulse frequency modulator and pulse width modulator can also be used, in order to shape the output of on-off thrusters. The PWPF modulator is here realized due to its advantages over other types of modulators. It is shown in Fig. 2 that the PWPF modulator is consists of a first order lag filter along with a Schmitt trigger inside a negative feedback loop. Generally, the PWPF introduces discontinuous and nonlinear control actions which may result in the worse control performance, but if they operate in pseudo linear range, the thrusters will act as continuous effectors [38-40].

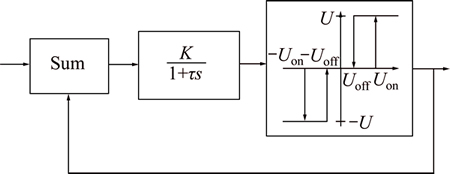
Fig. 2 Schematic diagram of PWPF

There are the parameters of the PWPF modulator, as shown in the present schematic diagram. The static characteristics parameters of the PWPF modulator are now tabulated in Table 1. The whole of parameters are taken into account in the process of modulator design. A consideration is performed to find the relationships between the static characteristics of the PWPF modulator in line with its parameters selection.

A thorough analysis of the PWPF parameters is considered by Krovel. There are some investigated results, as tabulated in Table 2, which can be used for initial parameters setting.

2.2.2 CA scheme realization

The realization of the CA scheme is to command on distribution logic, as an algorithm, whose function is to select specific thrusters and calculate their firing durations. It is to realize force and torque commands, which are derived from the control system of the spacecraft. This scheme is briefly given as

v_s(t)=Bu_s(t)                                  (8)

The advantage of the CA scheme is to deal with a number of actuators, separately and efficiently.In order to realize the CA scheme, a pseudo inverse matrix needs to be calculated. With this purpose, τ_x, τ_y and τ_z in association with T_i (i=1, 2, …, n) can be presented by the following

                                (9)

or there is

Table 1 Static characteristics parameters of PWPF modulator and its formula

Table 2 Recommended parameters of PWPF modulator

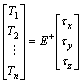                              (10)

Now, by supposing the number of thrusters to be eight, the following present matrices could be resulted.

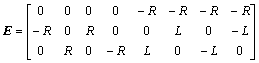    (11)

And there is

          (12)

The parameters R and L are highly variable with respect to the configuration of the thrusters in the spacecraft. It means that the results in the area of the CA scheme are directly based on the positions of thrusters. In such a case, the relation between E and E⁺ can easily be presented through E⁺=E^T(EE^T)^-1, as well. Now, the three-axis control torques in line with T_i (i=1, 2, …, 8) could clearly be calculated as

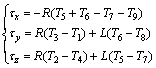                   (13)

It is apparent that the CA scheme may not be useful, since a number of on-off thrusters are employed. Due to the fact that T_i (i=1, 2, …, n) presented in Eq. (10), are in need of binary information, a relay, namely f_on/off has to be realized. 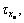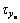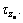In one such case, the generation of binary information for the whole of on-off thrusters are truly guaranteed, although the τ_x, τ_y and τ_z may be updated to and The relation of the thrusts in the three axes and its efficient ones can be presented by

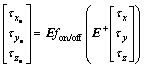                     (14)

It should be noted that the ε in the f_on/off could be optimized, in order to present the efficient thrusts in association with the corresponding ones.

2.2.3 Control approaches realizations

1）Three-axis PDLQR approach

The three-axis PDLQR approach is designed to handle the q_s, while the q_c is appeared in the outer control loop. The control coefficients should be acquired via LQR method to optimize its performance index. Here, the approach is realized through u_i=τ_i/I_i (i=1, 2, 3) along with the standard linear state space system to reach the

same performance index bywhile 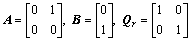and R_r=1/c² are taken, respectively. The PDLQR control effort; 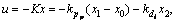is calculated to optimize the aforementioned performance index. Now, by supposing 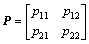as positive definite matrix, the Riccati equation, namely, A^*P+PA-PBR^-1B^*P+Q_r=0 can easily be dealt with to calculate the K_lqr= 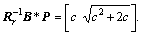Subsequently, the coefficients regarding the PDLQR approach are investigated through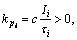 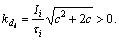Finally, the control efforts of the PDLQR approach are realized based upon the quaternion errors in association with the angular rates in the three axes by

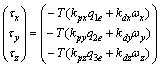                  (15)

By using 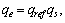its expanded form can be written by

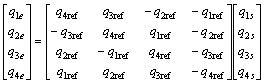   (16)

In one such case, the T_i (i=1, 2, …, 8) are the same for all the thrusters and also the conditions ||q_ref||=1 must be satisfied.

2) SMFC approach

Regarding the SMFC approach, it is first assumed that the measurements of both the spacecraft attitude and the angular rates are now available. Consider a nonlinear multi-input multi-output system of the form:

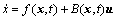                         (17)

where x[x₁ x₂ … x_n]^T and u[u₁ u₂ … u_m]^T are defined. Moreover, the condition |f(x,t)-f |≤F has to be satisfied. The uncertainties on the B can now be written in the multiplicative form B=I+△B. Let us consider e=x-x_d,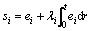and the stability condition; for each state, to realize the control

approach regarding the nonlinear system. It can be translated to find a control law for the vector u that verifies the aforementioned stability condition. Accordingly, it is easily possible to realize the control effort in the form of

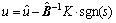                         (18)

where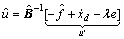and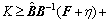 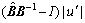are investigated. Now, the parametric uncertainties of spacecraft’s moments of inertia can be presented as

                                (19)

Afterwards, the △ can be acquired in the following form

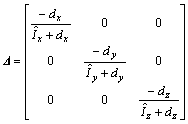              (20)

As is obvious, the upper bound of the f can be defined through F. By assuming Eq. (20), the results can finally be expressed by

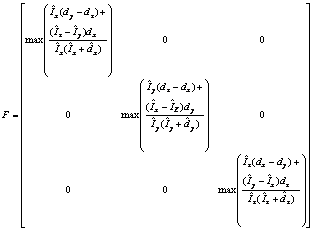 (21)

3) Stability analysis

Regarding the stability analysis in the proposed approach, at first, it should be noted that this is now organized and proved for the outer closed loop, as long as the inner closed loop has to be stable. It is possible, due to the fact that the process of designing the SMFC is considered, while the PWPF and the CA are taken into account in line with the spacecraft model. In fact, the present SMFC is realized to deal with a generalized model of the spacecraft, including the original model as well as its additive ones. Moreover, the uncertainties are known in the process of realizing the inner loop. Therefore, it is reasonable to focus on the outer loop, in order to illustrate the stability. It may be shown that the inner loop can be unstable, provided that some information regarding the realization of the SMFC may be missing. In this case, the present stability analysis needs to be generalized by assuming the unstable inner loop, as the corresponding disturbance, in the outer closed loop, which is here ignored to present. With this purpose, the Lyapunov function can first be written in accordance with the spacecraft quaternion vector, the referenced quaternion vector and also the angular rates in the three axes, in the outer closed loop, via

  (22)

where for simplicity, k_pu=k_p>0; μ=x, y, z is first assumed, although the present stability analysis is easy to prove for any values of k_pμ. The derivative of the present Lyapunov function is resulted by

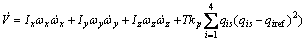 (23)

It is easy to rewrite the aforementioned derivative of the present Lyapunov function, in order to illustrate that the closed-loop control system is now stable, while the proposed control approach can be applied to the spacecraft, i.e.

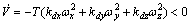              (24)

where 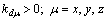has to be assumed.

3 Numerical simulations

The numerical simulations are conducted to verify the performance of the proposed control approach. In the predefined mission, it has to be able to track the commanded inputs. The nominal values of the spacecraft’s moments of inertia and also the PWPF parameters during the mission are all tabulated in Table 3.

By choosing c=5.0, T_i=1.0 N (i=1, 2, …, 8), R= 0.65 m and L=1 m, the coefficients of the PDLQR approach are designed, as tabulated in Table 4.

Figure 3 illustates the control efforts of the PDLQR approach in the three axes in the span of the simulation time.

And the errors of the present PDLQR approach are depicted in the there axes in Fig. 4. As are easily obvious, there are to be about zero in a finite time.

Table 3 Nominal spacecraft’s moments of inertia and PWPF parameters

Table 4 Coefficients of PDLQR approach realized in proposed approach

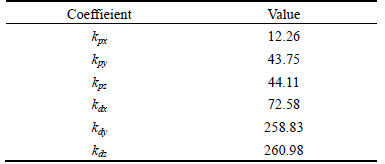
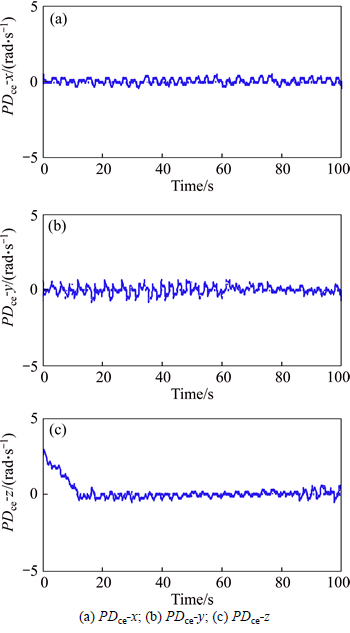
Fig. 3 Control effort regarding PDLQR approach in three axes:

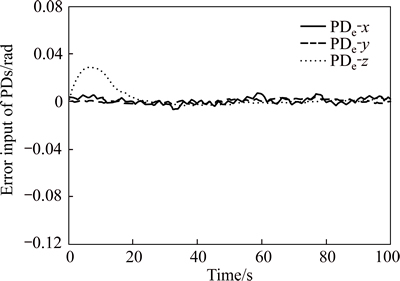
Fig. 4 Errors regarding PD approach in three axes

The SMFC control efforts in the three axes including SMFC_ce-x, SMFC_ce-y and SMFC_ce-z are all illustrated in Fig. 5, respectively.

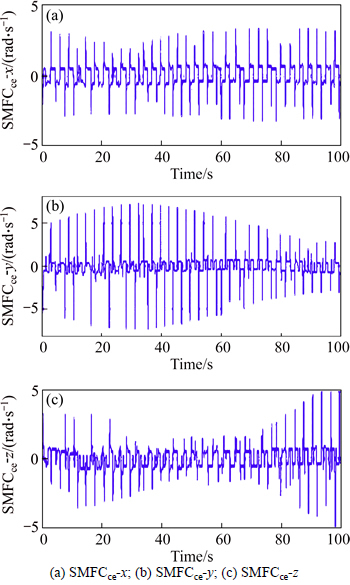
Fig. 5 Control effort regarding SMFC approach in three axes:

Moreover, the SMFC surfaces in the three axes including SMFC_surf-x, SMFC_surf-y and SMFC_surf-z are all illustrated in Fig. 6, respectively.

The PWPF modulator results in the three axes including PWPF_out-x, PWPF_out-y and PWPF_out-z are all now presented in Fig. 7, respectively. As are now obvious, there are three modulated pulses, which their amplitudes are all restricted as -1 and 1.

Afterwards, the control torques in the three axes including control torque-x, control torque-y and control torque-z are all shown in Fig. 8, respectively.

Now, by using eight on-off thrusters in the approach proposed here, based on the CA scheme outcomes, the inputs of them, i.e. T_i=u_i (i=1, 2, …, 8) are all depicted in Figs. 9(a)-(b). Due to the fact that these on-off thrusters should be dealt with through the present illustrated signals, they are now taken as 0 and +1. Moreover, Figs. 10(a)-(b) illustrate the number of thruster’s triggers, in order to reach the consumable energy, in general. It aims us to see the applicability of each one of the thrusters in the period of simulation time.

The angular rates in the three axes in the inner closed loop are all illustrated in Fig. 11, respectively. The results indicate that the proposed control approach is truly able to deal with these angular rates, since the commands are abruptly varying with respect to time.

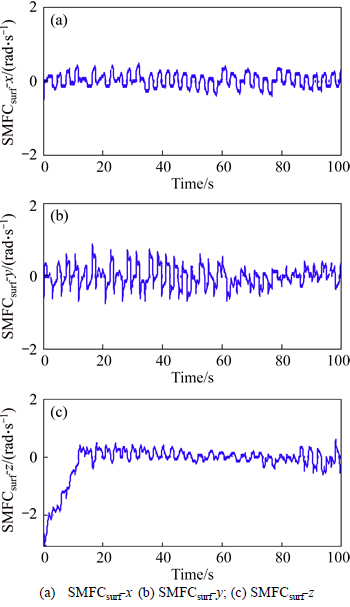
Fig. 6 SMFC surfaces in three axes:

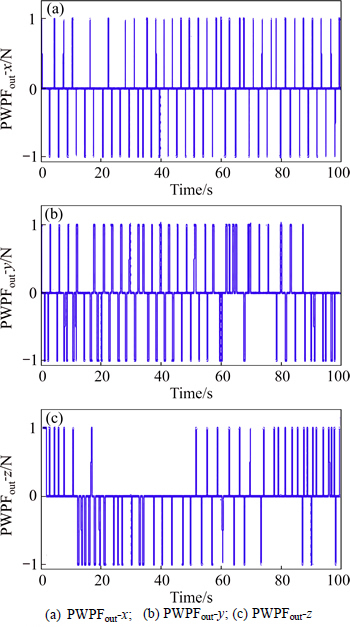
Fig. 7 PWPF modulator results in three axes:

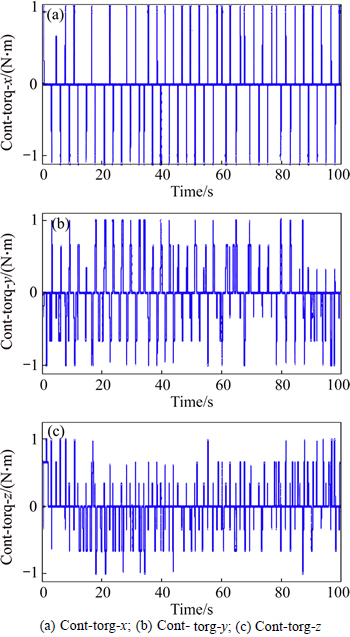
Fig. 8 Control torques in three axes:

The quaternion vector in the outer closed loop are all illustrated in Fig. 12, respectively. The results indicate that the proposed control approach can track these corresponding commands, which are suddenly varying with respect to time.

Subsequently, the Euler angles in the three axes including φ, θ, ψ in degree are all tracked, in the appropriate manners, with respect to the corresponding commands, i.e. φ_c, θ_c, ψ_c, as shown in Fig. 13. It should be noted that the information regarding this figure is the same as Fig. 12. Here, the initial values for commands and the spacecraft including φ₀=φ_c0=0°, θ₀=θ_c0=20° and ψ₀=ψ_c0=60° are first taken as the same in the present experiment. The investigation results indicate the appropriate outcomes are apparently acquired by varying the commands in the three axes in the span of simulation time.

In order to consider the performance of the proposed approach more, the further experiment is now carried out by changing the initial values of the spacecraft to be zeros, i.e. φ₀=θ₀=ψ₀=0°in the three axes, while the initial values of the commands are taken as φ_c0=0°; θ_c0=20° and ψ_c0=60°, as shown in Fig. 14, as the experiment 2. Moreover, the simulations are run one more time, in the experiment 3, by changing the initial values of the spacecraft to be φ₀=22°, θ₀=-40°and ψ₀=0° in the three axes, while the corresponding initial values of the commands are taken as φ_c0=0°; θ_c0=20° and ψ_c0=60°, as shown in Fig. 15.

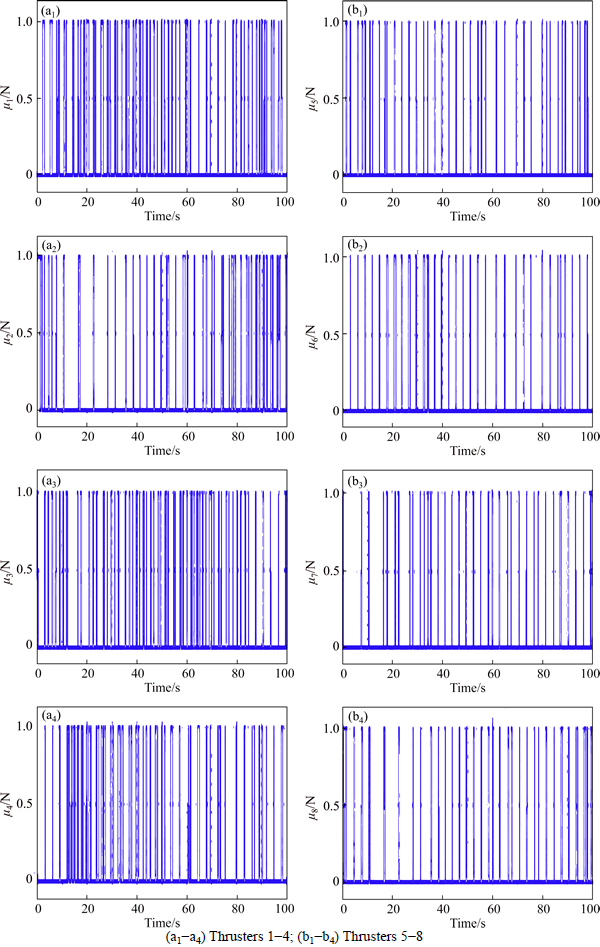
Fig. 9 On-off thruster’s inputs:

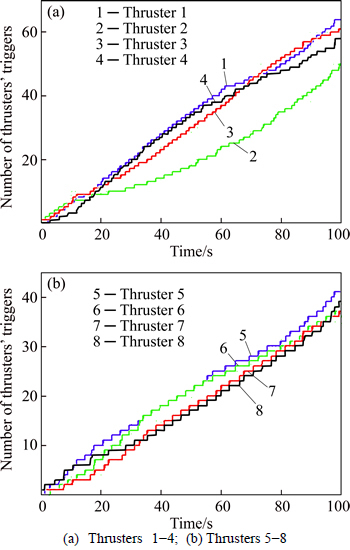
Fig. 10 Number of thruster’s triggers:

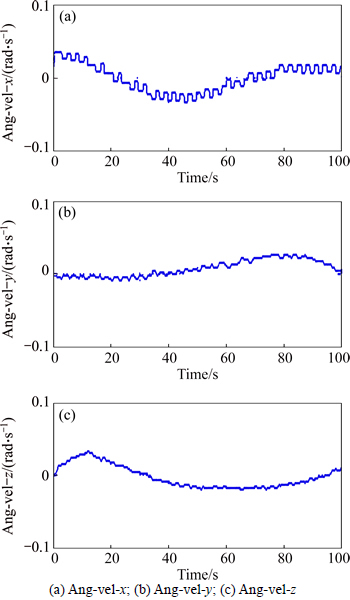
Fig. 11 Angular rates in three axes in inner closed loop:

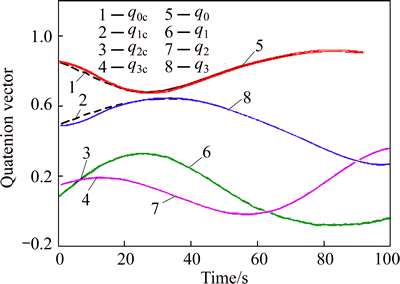
Fig. 12 Quaternion vector in outer closed control loop with respected to corresponding commands

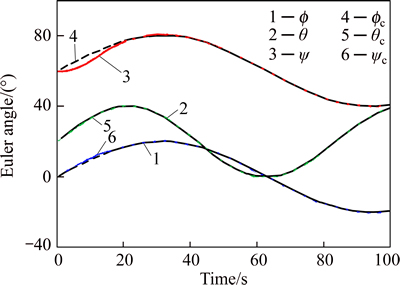
Fig. 13 Euler angles tracking with respected to corresponding commands via proposed approach (Experiment 1)

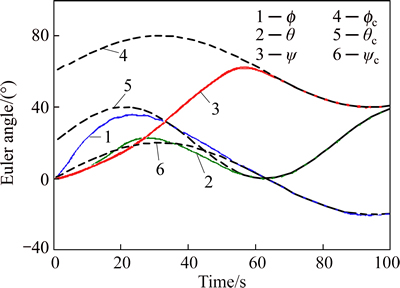
Fig. 14 Euler angles tracking with respected to corresponding commands via proposed approach (Experiment 2)

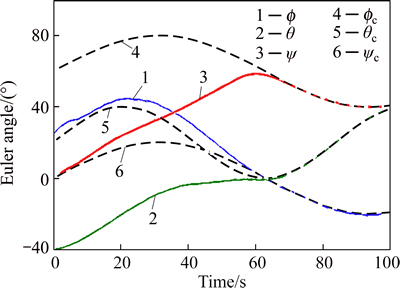
Fig. 15 Euler angles tracking with respected to corresponding commands via proposed approach (Experiment 3)

To consider the results, investigated in the proposed approach, the traditional PD approach with the same coefficients of the PDLQR approach is realized and simulated to compare as a benchmark, shown in Fig. 16. As are now clear, the results indicate that referenced commands are somehow tracked with the errors.

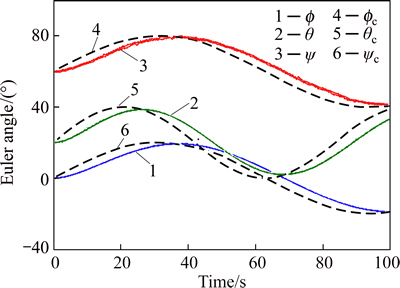
Fig. 16 Euler angles tracking with respected to corresponding commands via PD benchmark (Approach-3)

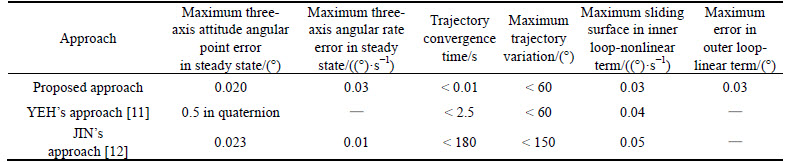
Also, in order to consider the results more, two references, published in the recent years, are now chosen to compare as other benchmarks. With this purpose, the Yeh approach is to realize two nonlinear attitude controllers, including the sliding mode attitude tracking controller in association with the sliding mode adaptive attitude tracking controller in the area of spacecraft with thrusters, in order to follow the predetermined trajectory in space through the spacecraft’s attitude control. Hereinafter, the Yongqiang approach is to realize a number of types of time-varying sliding mode attitude control tracking approach in a rigid spacecraft under known or measurable desired attitude trajectory. These research organization are somehow comparable with respect to the present research work. There are the following criteria to be considered in Table 5 including 1) maximum three-axis attitude angular points errors in steady state, 2) maximum three-axis angular rates errors in steady state, 3) trajectory convergence time, 4) maximum trajectory variations, 5) maximum sliding surface in the inner closed loop; nonlinear term, and finally 6) maximum errors in the outer closed loop; linear term, which are all important to evaluate the approach performances w.r.t. the corresponding benchmarks. As a deduction matter, the results indicate that the proposed approach is now well behaved in line with both benchmarks regarding the items 1) and 5), although the Yongqiang approach is also well behaved regarding the item 2) w. r. t. two present considerable approach and finally the Yeh approach is somehow well behaved regarding item 5) w. r. t. the Yongqiang approach, as well.

4 Conclusions

A new quaternion based three-axis attitude finite- time control approach is proposed. The control idea presented here is realized based on a new hybrid linear-nonlinear control approaches in the inner and the outer closed loops. In this case, the PDLQR approach is realized in the outer closed loop as the linear control to cope with the quaternion vector in line with the corresponding rotation angles of the spacecraft, as long as the SMFC approach is also realized in the inner closed loop, as the nonlinear control to cope with the angular rates of the same spacecraft. It is shown that the inner closed loop of the proposed control approach is organized in line with the PWPF to deal with a number of on-off thrusters, as system actuators, of overactuated spacecraft. An increased number of the present on-off thrusters is possible through CA scheme, in order to provide overall performance of the present overactuated spacecraft, in a constructive manner.

Acknowledgments

The corresponding author would like to express the best and the warmest regards to the respected Editors of “Journal of Central South University”, Springer Publisher, as well as the whole of respected potential anonymous reviewers, for suggesting their impressive, constructive, desirable and technical comments on the present investigation in all rounds of processing. Moreover, Dr. Mazinan sincerely appreciates the Islamic Azad University (IAU), South Tehran Branch, Tehran, Iran for sufficient supports in the process of research investigation and organization that is carried out under contract “entitled “control allocation under constraints via pseudo inverse matrix for a set of actuators in complicated systems”with Research Department. At last, special thanks to Mrs. Maryam Aghaei Sarchali, Miss Mohadeseh Mazinan and also Mr. Mohammad Mazinan for the efficient assistance and patience, in the procedure of realizing the present outcomes.

Table 5 Proposed approach performance verification w.r.t. corresponding benchmarks

Nomenclature

f, θ, ψ

Euler angles of spacecraft

f₀, θ₀, ψ₀

Initial values for commanded Euler angles of the spacecraft

f_c, θ_c, ψ_c

Commanded Euler angles

f_c0, θ_c0, ψ_c0

Initial values for commanded Euler angles

q_s

Spacecraft quaternion vector containing q_is; i=1, 2, 3, 4

q_ref

Referenced quaternion matrix containing q_ijref; i=1, 2, 3, 4

q_e

Quaternion vector error containing q_ie; i=1, 2, 3, 4

q_c

Quaternion vector command containing q_ic; i=1, 2, 3, 4

K_pw

PWPF gain

τ_pw

PWPF constant time

U_on

PWPF switch on

H

PWPF hysteresis

U_off

PWPF switch off

f_on/off

On-off relay

u_s

Real control regarding the CA

v_s

Virtual control regarding the CA

B_s

Constant matrix regarding the CA

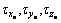
Three-axis efficient thrusts

τ_c

Control torque vector

T_i

ith thruster’s level

S_i

Sliding surface at ith instant of time

n_i

ith eigenvector of rotation

x

State vector

u

System inputs

A

State matrix

B

Input matrix

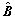
Nominal value regarding B

Q_r

Diagonal matrix regarding the performance index

R_r

Positive scalar coefficient regarding the performance index

R

Thruster’s arm radius

L

Thruster’s length

K

Diagonal matrixes containing k_i; i=1, …, n

K_lqr

LQR gain

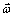
Angular rates vector in the body coordinate

ω

Angular rates vector

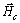
Angular momentum vector in the body coordinate

H_μ

Three-axis angular momentum of the spacecraft in the μ direction

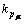
Three-axis proportional gain of the PDLQR approach in the μ direction

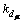
Three-axis derivative gain of the PDLQR approach in the μ direction

d_μ

Three-axis variation of moments of inertia in the μ direction

ω_μ

Three-axis angular rates of the spacecraft in the μ direction

τ_μ

Three-axis control torque of the spacecraft in the μ direction

I_μ

Three-axis moment of inertial of the spacecraft in the μ direction

I

Moments of inertial matrix

△

Additive uncertainty matrix

V

Lyapunov function

F

Known function

F

Bounded function regarding F

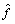
Estimated nonlinear or time-varying function

η

Diagonal matrixes containing η_i; i=1, …, n

e

Tracking error vector

ε_r

Angle of rotation

ε

On-off relay hysteresis

List of Acronyms

HRTAC

Hybrid robust three-axis attitude finite- time control

PDLQR

PD based LQR

PWPF

Pulse-width pulse-frequency

PMS

Pulse modulation synthesis

SMFC

Sliding mode finite-time control

CA

Control allocation

References

[1] JIN Er-dong, JIANG Xiao-lei, SUN Zhao-wei. Robust decentralized attitude coordination control of spacecraft formation [J]. Systems & Control Letters, 2008, 57(7): 567-577.

[2] BUSTAN D, PARIZ N, SANI S K H. Robust fault-tolerant tracking control design for spacecraft under control input saturation [J]. ISA Transactions, 2014, 53(4): 1073-1080.

[3] LU Kun-feng, XIA Yuan-qing, FU Meng-yin. Controller design for rigid spacecraft attitude tracking with actuator saturation [J]. Information Sciences, 2013, 220: 343-366.

[4] PUKDEBOON C, ZINOBER A S I. Control Lyapunov function optimal sliding mode controllers for attitude tracking of spacecraft [J]. Journal of the Franklin Institute, 2012, 349(2): 456-475.

[5] MAZINAN A H, PASAND M, SOLTANI B. Full quaternion based finite-time cascade attitude control approach via pulse modulation synthesis for a spacecraft [J]. ISA Transactions, 2015, 58: 567-585.

[6] MAZINA N. A Lyapunov-based three-axis attitude intelligent control approach for unmanned aerial vehicle [J]. Journal of Central South University, 2015.

[7] MAZINAN A H. On spacecraft maneuvers control subject to propellant engine modes [J]. ISA Transactions, Elsevier Publisher, 2015, 58: 222-236.

[8] MAZINAN A H, KHALAJI A R. TADC: A new three-axis detumbling mode control approach [J]. International Journal of Dynamics and Control, 2015: 1-10.

[9] MAZINAN A H. High-precision full quaternion based finite-time cascade attitude control strategy considering a class of overactuated space systems [J]. Human-centric Computing and Information Sciences, 2015: 1-14.

[10] MAZINAN A H. High-precision three-axis detumbling and pointing attitude control strategy for a class of complicated space systems [J]. International Journal of Dynamics and Control, 2015: 1-22.

[11] YEH F K. Sliding-mode adaptive attitude controller design for spacecrafts with thrusters [J]. IET Control Theory and Applications, 2010, 4(7): 1254-1264.

[12] JIN Yong-qiang, LIU Xiang-dong, QIU Wei, HOU Chao-zhen. Time-varying sliding mode controls in rigid spacecraft attitude tracking [J]. Chinese Journal of Aeronautics, 2008, 21: 352-360.

[13] MORADI M. Self-tuning PID controller to three-axis stabilization of a satellite with unknown parameters [J]. International Journal of Nonlinear Mechanics, 2013, 49: 50–56.

[14] JIN Yong-qiang, LIU Xiang-dong, QIU Wei, HOU Chao-zhen. Time-varying sliding mode controls in rigid spacecraft attitude tracking [J]. Chinese Journal of Aeronautics, 2008, 21(4): 352-360.

[15] WU Jin-jie, LIU Kun, HAN Da-peng. Adaptive sliding mode control for six-DOF relative motion of spacecraft with input constraint [J]. Acta Astronautica, 2013, 87: 64-76.

[16] JIANG Ye, HU Qing-lei, MA Guang-fu. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures [J]. ISA Transactions, 2010, 49(1): 57-69.

[17] BUTYRIN S A, MAKAROV V P, MUKUMOV R R, SOMOV Y E, VASSILYEV S N. An expert system for design of spacecraft attitude control systems [J]. Artificial Intelligence in Engineering, 1997, 11(1): 49-59.

[18] HU Qing-lei, ZHANG Jian. Relative position finite-time coordinated tracking control of spacecraft formation without velocity measurements [J]. ISA Transactions, 2014, 54: 60-74.

[19] FRESK E. NIKOLAKOPOULOS G. Full quaternion based attitude control for a quadrotor [C]// European Control Conference (ECC), 2013: 3864-3869.

[20] SABATINI M, PALMERINI G B, LEONANGELI N, GASBARRI P. Analysis and experiments for delay compensation in attitude control of flexible spacecraft [J]. Acta Astronautica, 2014, 104(1): 276-292.

[21] ZHENG Zhong, SONG Shen-min. Autonomous attitude coordinated control for spacecraft formation with input constraint, model uncertainties, and external disturbances [J]. Chinese Journal of Aeronautics, 2014, 27(3): 602-612.

[22] YANG Hong-jiu, YOU Xiu, XIA Yuan-qing, LIU Zhi-xin. Nonlinear attitude tracking control for spacecraft formation with multiple delays [J]. Advances in Space Research, 2014, 54(4): 759-769.

[23] HUO Xing, HU Qing-lei, XIAO Bing. Finite-time fault tolerant attitude stabilization control for rigid spacecraft [J]. ISA Transactions, 2014, 23(2): 241-250.

[24] DU Hai-bo, LI Shi-hua. Attitude synchronization control for a group of flexible spacecraft [J]. Automatica, 2014, 50(2): 646-651.

[25] SONG Zhan-kui, LI Hong-xing, SUN Kai-biao. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique [J]. ISA Transactions, 2014, 53(1): 117-124.

[26] LU Kun-feng, XIA Yuan-qing. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence [J]. Automatica, 2013, 49(12): 3591-3599.

[27] YANG Y. Spacecraft attitude determination and control: Quaternion based method [J]. Annual Reviews in Control, 2012, 36(2): 198-219.

[28] ZOU An-min, dev KUMAR K. Adaptive fuzzy fault-tolerant attitude control of spacecraft [J]. Control Engineering Practice, 2011, 19(1): 10-21.

[29] MOUSAVI F, ROSHANIAN J, EMAMI M R. Hardware-in-the-loop simulation for attitude control of a suborbital module using cold gas thrusters [J]. Modares Mechnicl Engineering, 2014, 14(10): 177-186.

[30] WIE B, BARBA P M. Quatenion feedback for spacecraft large angle maneuvers [J]. Journal of Guidance, 1985, 8: 360-365.

[31] HU Qing-lei, LI Bo, ZHANG You-min. Robust attitude control design for spacecraft under assigned velocity and control constraints [J]. ISA Transactions, 2013, 52(4): 480-493.

[32] CAI He, HUANG Jie. The leader-following attitude control of multiple rigid spacecraft systems [J]. Automatica, 2014, 50(4): 1109-1115.

[33] KUO Yong-lin, WU Tsung-liang. Open-loop and closed-loop attitude dynamics and controls of miniature spacecraft using pseudowheels [J]. Computers & Mathematics with Applications, 2012, 64(5): 1282-1290.

[34] ZHANG Xu-xi, LIU Xian-ping, ZHU Qi-dan. Attitude control of rigid spacecraft with disturbance generated by time varying exosystems [J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(7): 2423-2434.

[35] JOHANSEN TOR A, FOSSEN THOR I. Control allocation—A survey [J]. Automatica, 2013, 49(5): 1087-1103.

[36] ZACCARIAN L. Dynamic allocation for input redundant control systems [J]. Automatica, 2009. 45(6): 1431-1438.

[37] SERVIDIA P A. Control allocation for gimballed/fixed thrusters [J]. Acta Astronautica, 2010, 66(3/4): 587-594.

[38] VADALI S R. Variable-structure control of spacecraft large-angle maneuvers [J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 235-239.

[39] JIE Geng, SHENG Yong-zhi, LIU Xiang-dong. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system [J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976.

[40] T D. Optimal tuning of PWPF modulator for attitude control [D]. Moscow: Eng. Cybern 2005.

(Edited by DENG Lü-xiang)

Received date: 2015-05-04; Accepted date: 2015-09-22

Corresponding author: A. H. Mazinan; Tel: +98-21-33722831-5x3211; E-mails: mazinan@azad.ac.ir, ahmazinan@gmail.com, ah_mazinan@yahoo.com