DOI： 10.11817/j.issn.1672-7207.2019.12.013

单轴压缩条件下平行双裂隙演化机理的颗粒流分析

李勇^{1, 2},蔡卫兵^{1, 2},朱维申¹,董振兴^{1, 2},张强勇^{1, 3}

（1. 山东大学 岩土与结构工程研究中心，山东 济南，250061；

2. 山东大学 齐鲁交通学院，山东 济南，250061；

3. 山东大学 土建与水利学院，山东 济南，250061）

摘要:基于离散元理论，研究含平行双裂隙的水泥砂浆试件在不同裂隙倾角和单轴压缩下裂纹萌生、扩展、搭接及贯通机理，并从应力场和位移场的角度分析裂纹扩展演化规律。研究结果表明：当裂隙倾角=30°时，翼裂纹在最大应力降的作用下沿着垂直裂隙平面方向扩展至一定长度后将保持较长时间不变，直到次生裂纹大量出现后，裂隙外侧的翼裂纹才会在最大拉应力的作用下沿着最大加载方向继续扩展；在萌生初期，次生裂纹的出现会削弱了裂隙尖端的压应力集中效应，同时抑制裂隙内侧翼裂纹的扩展，最大拉应力集中在裂隙之间导致次生裂纹一般都是瞬时成片出现，且形成的裂纹的宽度远大于翼裂纹的宽度；翼裂纹主要是由颗粒之间的相对拉伸或直接拉伸产生；次生裂纹SC-1以拉裂纹的形式优先出现在裂隙尖端R1和R2之间，随着轴向应力增加，SC-1处萌生的新裂纹为拉剪复合型裂纹。

关键词:裂纹扩展；离散元；应力场；位移场

中图分类号:TU45    文献标志码:A     文章编号:1672-7207（2019）12-3035-11

Particle flow analysis of parallel double crack evolution under uniaxial compression

LI　Yong^{1, 2}, CAI　Weibing^{1, 2}, ZHU　Weishen¹, DONG　Zhenxing^{1, 2}, ZHANG　Qiangyong^{1, 3}

(1. Geotechnical & Structural Engineering Research Center, Shandong University, Jinan 250061, China；

2. School of Qilu Transportation, Shandong University, Jinan 250061, China；

3. School of Civil Engineering, Shandong University, Jinan 250061, China)

Abstract: The mechanism of crack initiation, propagation, and overlap in cement mortar specimens with parallel double pre-existing flaws under different fracture dip angles and uniaxial compression was investigated based on the discrete element theory. Stress field and displacement field were employed to analyze the evolution of crack propagation. The results show that when the crack inclination angle reaches 30°, the wing crack remains unchanged for a long time until the secondary crack occurs after propagating under the maximum stress drop along the vertical crack plane direction, and the wing crack on the outer side of the crack continues to expand along the maximum loading direction under the action of maximum tensile stress; At the early stage of initiation, the occurrence of secondary cracks weakens the compressive stress concentration at the crack tip and inhibits the crack propagation inside the flaw. Before the secondary crack initiation, the tensile stress is relatively large in a region between the fractures. Therefore, the secondary cracks are generally instantaneously formed, and the width of the crack formed is much larger than the width of the wing crack. The maximum tensile stress concentrated between the cracks contributes to the appearance of secondary crack with instant and much wider than that of the wing crack. Wing cracks are mainly initiated by relative or direct stretching between particles. Secondary crack SC-1 preferentially appears between crack tips R1 and R2 as tensile cracks and transforms into tensile-shear composite crack with the increasing axial stress.

Key words: crack propagation; discrete element; stress field; displacement field

裂隙岩体作为一种复杂的工程地质体，是采矿、水电、铁路、地下空间等重大工程中经常遇到的重要施工对象之一，在高地应力作用下，裂纹之间相互搭接、贯通会造成岩体损伤甚至破坏，最终往往威胁到工程建设的稳定和安全，因此，深入研究裂纹扩展演化规律具有重要的理论价值和工程意义。为了了解不同天然材料和类岩石材料裂纹扩展规律，国内外学者开展了大量物理实验研究。BOBET等^[1-2]在试件开裂过程中观察到拉伸裂纹、混合张拉剪切裂纹和剪切裂纹，研究了翼裂纹和次生裂纹的起裂和扩展机制，总结了裂纹扩展演化规律。ZHAO等^[3]研究了含2条平行闭合裂隙的类岩石材料在单轴压缩条件下裂纹扩展演化和应力应变规律，分析了裂隙倾角对裂隙尖端应变浓度的影响。张晋勋等^[4]研究了平行双裂隙在三轴压缩条件下裂纹搭接贯通模式，分析了裂隙产状对岩体力学性质和破裂模式的影响。黄彦华等^[5]通过对含断续双裂隙的类岩石材料进行三轴压缩试验，分析了裂隙倾角对岩样强度及变形破坏特征的影响。由于数值方法的快速性和方便性，数值模拟已广泛应用于研究材料变形破坏机理。与有限元分析相比，由CUNDALL^[6]提出的离散单元法不考虑复杂的本构关系，不仅能够有效分析裂纹扩展过程和解释物理实验中观察到的裂纹类型，还能从细观力学的角度深入阐述裂纹的扩展机制和贯通模式，其中，基于离散单元法建立的平行黏结模型已经广泛应用于岩石破坏分析中。YANG等^[7-8]采用颗粒流模拟砂岩在单轴压缩下的力学特征，深入探讨了岩石裂纹扩展演化机理及细观力学响应机制。袁康等^[9]基于颗粒流方法对岩石在压缩荷载作用下内部颗粒的宏细观力学响应进行研究，得到岩石压缩破坏过程中颗粒旋转弧度颗粒间接触力、颗粒竖向位移以及细观裂纹的演化过程。胡训健等^[10]采用Flat-Joint模型模拟了含2条断续裂隙试件的直接拉伸试验，分析了裂隙倾角和岩桥倾角对抗拉强度和裂纹扩展的影响。PENG等^[11]基于PFC-GBM模拟研究了晶粒粒径-粒度比对材料变形强度、微裂纹行为和诱发微裂纹形态的影响。研究结果^[12-17]表明，颗粒流适用于岩石断裂和大变形分析的研究，有助于了解裂纹扩展规律和裂纹细观演化机制。岩体的破坏过程是一个由微裂纹萌生到局部破坏再到大规模破坏的过程，在加载过程中，岩石颗粒的受力状态和位移模式决定裂纹的类型和扩展方向。ZHANG等^[18-19]基于颗粒流的数值方法研究裂纹附近应力场和位移场的变化规律，有效分析了不同类型裂纹的萌生机理。虽然前人已采用PFC程序对裂纹扩展进行了深入研究，但是从细观力学的角度分析裂纹扩展的研究较少，而且已有研究主要针对裂纹扩展的整体描述，不能细致分析裂纹扩展演化规律。在此，本文作者采用PFC程序模拟含预制平行双裂隙的水泥砂浆试件在单轴压缩条件下裂纹扩展演化规律，通过布置测量圆来定量监测裂纹扩展过程中裂隙尖端应力场的变化，同时通过分析颗粒的位移场和最大主应力方向细致研究裂纹在不同加载阶段的性质和形成机理。

1 室内试验

1.1　试件制备及试验方法

采用水泥砂浆作为类岩石材料进行室内单轴压缩试验，其原料42.5R普通硅酸盐水泥、石英砂和水的质量比为1:2.34:1.35，为保持水泥砂浆的和易性，在制备试件时添加了少量的减水剂。水泥砂浆材料测试参数如表1所示，物理力学性能与砂岩等典型岩石材料接近，其拉压强度比接近1:10，属于高脆性材料，因此可作为类岩石材料来研究裂纹扩展演化规律。

表1　水泥砂浆材料与砂岩的物理力学参数对比

Table 1　Comparison of physical and mechanical parameters between cement mortar materials and sandstone

试验采用的水泥砂浆试件长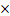宽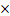高为7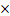0 mm40 mm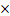140 mm。在搅拌水泥砂浆之前将2片宽厚为12.0 mm1.2 mm的薄铁片固定在模具中，并在薄铁片表面涂上少许环氧树脂，待水泥砂浆材料在模具中成形养护24 h后，再将薄铁片全部拔出，从而形成二维平行贯穿裂隙。水泥砂浆试件和预制平行双裂隙的尺寸示意图如图1所示，其中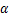，为预制裂隙与水平方向的夹角。

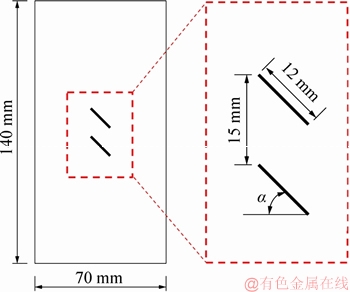
图1　水泥砂浆试件与预制平行双裂隙尺寸示意图

Fig. 1　Schematic diagram of cement mortar specimen and pre-existing double flaw size

为研究裂隙倾角对岩体力学性质和破坏过程的影响，裂隙倾角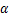取为30°，45°和60°，平行预制裂隙间距为15 mm，布置在试件的中心区域。每个裂隙倾角制备6个水泥砂浆试件(共计18个试件)，取试验数据平均值进行分析。

1.2　细观参数校核

水泥砂浆试件数值模型的颗粒接触采用平行黏结模型，当轴向应力降到峰值应力的50%时停止加载。ZHANG等^[20]研究了在单轴加载下加载速率对试件开裂和破坏模式的影响，为确保数值模型在加载过程中保持静态平衡，数值模型位移加载速率取为0.08 m/s。在PFC中，通过对标准试件进行室内压缩试验来校核细观参数至关重要，试件宏观力学性质由颗粒之间细观参数决定。黏聚力和内摩擦角影响试件的破坏模式和微裂纹的类型，颗粒之间的摩擦因数对试件的起裂应力、峰值应力以及弹性模量等重要参数的影响较小^[21-23]。在已有研究基础上，结合水泥砂浆材料的特性，通过试错法不断调整细观参数使数值模拟得出的基本力学参数与完整标准试件的物理实验基本一致，由于水泥砂浆属于脆性材料，因此需进一步微调黏聚力和内摩擦角，使数值模拟得到的试件破坏模式与室内试验的接近，破坏模式对比图如图2所示，最终力学参数和细观参数分别如表2和表3所示，其中，表2中数值模拟参数为最终得到的宏观力学参数，与数值模拟采用的细观参数不同。

由图2可知，水泥砂浆试件整体破坏主要是次生裂纹大量生成并迅速贯通形成的剪切带所致，当裂隙倾角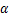为45°时，试件整体破坏时剪切破坏带的轨迹与30°和60°的相反，但是平行双裂隙外侧尖端翼裂纹的扩展方向依然没变。

图3所示为单轴加载下室内实验和数值模拟的应力应变曲线对比图。由图3可知，不同裂隙倾角下，室内试验得到的峰值强度与数值模拟的结果相差不大，在弹性阶段，室内试验与数值模拟的压缩模量基本一致。可见，PFC标定的细观参数较为合理。值得注意的是，由于水泥砂浆材料在试件成型过程中会产生一定的缺陷，在加载的初始阶段，应力-应变曲线会出现非线性阶段，而在PFC中，模拟获得的应力-应变曲线无法体现初始压密阶段，因此，室内试验的峰值应变要大于数值模拟的峰值应变，在进行细观参数校核时，只需对弹性阶段的应变量和弹性模量进行校核。在图3中，应力-应变曲线出现了应力降^[24]，对于数值模拟曲线，主要是在加载作用下次生微裂纹开始大量生成，并且相互搭接贯通，逐渐开始形成宏观裂纹所致；对于室内试验曲线，主要是在试件初始压密阶段的微裂纹闭合所致。此外，随着裂隙倾角增加，数值模拟的峰值强度逐渐增加，分别为46.55，49.56和57.66 MPa。然而，传统理论认为含45°结构面岩体的峰值强度最小，这是由于本文采用的预制裂隙尺寸相对较小，裂隙倾角在低角度时对峰值强度的影响比高角度时的小，以及试件在浇筑的过程中存在不可避免的误差所致。

图2　室内试验与数值模拟破坏模式对比图

Fig. 2　Comparison of failure mode between laboratory experiment and numerical simulation

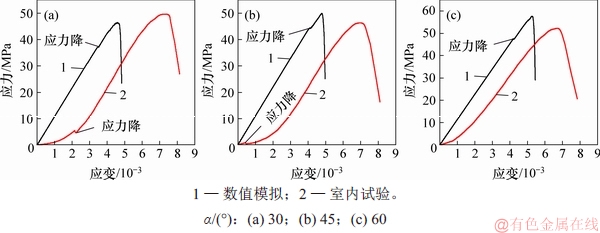
图3　单轴加载下室内试验与数值模拟应力-应变对比

Fig. 3　Comparison diagram of stress and strain between laboratory test and numerical simulation under uniaxial loading

表2　完整水泥砂浆试件物理实验与数值模拟物理力学参数对比

Table 2　Comparison of physical and mechanical parameters between complete cement mortar specimens and numerical simulation

表3　数值模型的细观参数

Table 3　Microscopic parameters of numerical model

2 数值模拟结果分析

将预制裂隙尖端首次起裂并沿加载方向扩展的裂纹称为翼裂纹，翼裂纹产生之后萌生的裂纹称为次生裂纹，在PFC数值模拟中，只能通过颗粒接触断裂时的应力状态来区分张拉微裂纹和剪切微裂纹，为进一步细化分类，通过比较颗粒接触发生断裂时承受的荷载与黏聚力将剪切微裂纹细分为拉剪微裂纹和压剪微裂纹。以裂隙倾角α为30°时为例，研究裂纹扩展演化规律。

2.1　裂纹扩展机制

应力场对于分析岩石材料的裂纹演化机理至关重要，然而基于离散元理论开发的PFC不能直接获取应力场，因此，需要通过设置应力圆^[25]来监测试样在加载过程中应力场变化，再将得到的数据导入处理软件来生成应力云图。测量圆布置图如图4所示，其中，L1，R1，L2和R2表示裂隙尖端，应力圆半径取为1 mm，每个应力圆中包含的颗粒数为15~20个。

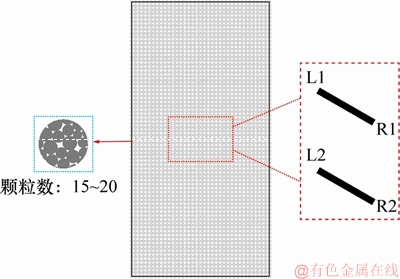
图4　测量圆布置示意图

Fig. 4　Schematic diagram of measuring circle layout

图5所示为应力与微裂纹数目随应变变化曲线图，其中点a，b，c，d和e对应的应力分别为31.52，37.35，45.2，46.55和36.48 MPa。由图5可知，微裂纹增长可分为张拉微裂纹萌生阶段(ab)、微裂纹稳定扩展阶段(bd)和微裂纹快速增长阶段(de)。微裂纹在a点萌生后增长缓慢，直到轴向应力加载至峰值点附近，微裂纹才会大规模扩展，试样进入全面破坏阶段，其微裂纹增长速度随应变近似呈指数关系增加。

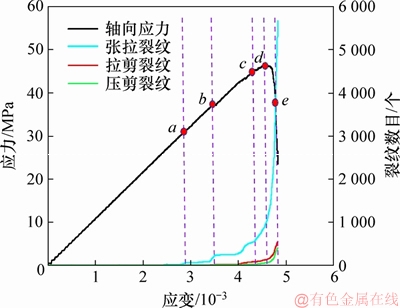
图5　=30°时应力与微裂纹数目随应变变化曲线

Fig. 5　Curve diagram of stress and number of micro-cracks with strain change at =30°

由于试样的最终破坏模式受多因素影响，只选取a，b，c和d 4个加载点进行应力场和位移场分析。图6和图7所示分别为裂纹扩展演化和最大主应力演化示意图，图6中WC和SC分别为翼裂纹和次生裂纹，带箭头的虚线代表裂纹的扩展方向，图7中细实线为拉应力和压应力的分界线，应力云图中，拉应力为正，压应力为负。

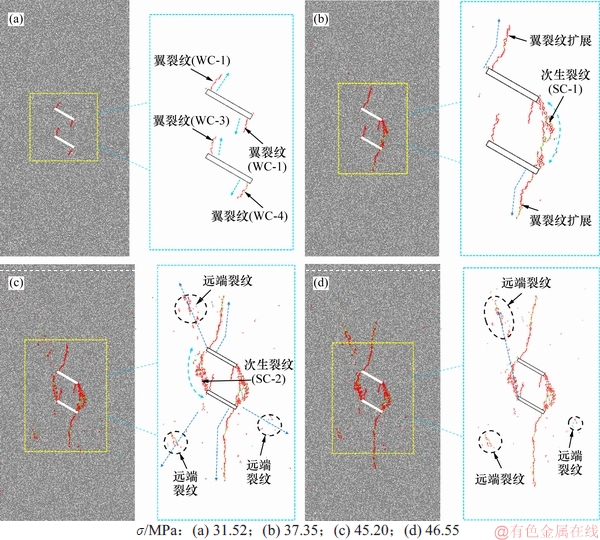
图6　单轴加载下裂纹扩展演化图

Fig. 6　Evolution of crack propagation under uniaxial loading

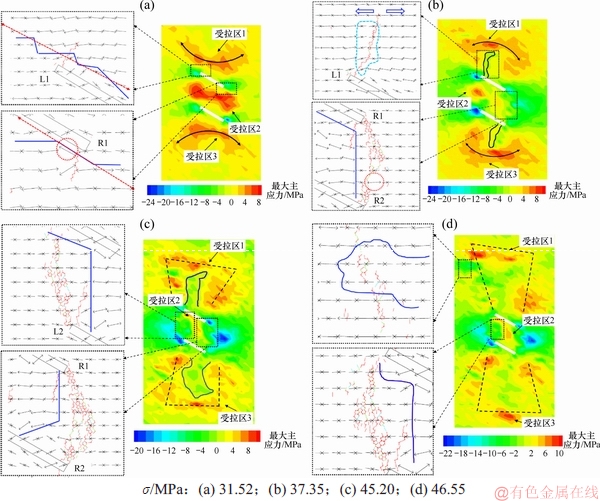
图7　最大主应力演化示意图

Fig. 7　Schematic diagram of maximum principal stress evolution

为研究方便，将试样中心上方和下方的裂隙分别记为CK-1和CK-2。由图6(a)可知，当轴向应力加载至a点(31.52 MPa)时，翼裂纹WC-1，WC-2，WC-3和WC-4萌生在预制裂隙的尖端，裂纹初始扩展方向与预制裂隙平面基本垂直，其中WC-1和WC-4的扩展长度较长，大致与裂隙长轴相等。由图7(a)可知，平行预制裂隙之间的受拉区2呈哑铃状分布，其主应力最大；根据拉应力的分布状态将其分为受拉区1，2和3，CK-1正上方的受拉区1呈凹形分布，CK-2正下方的受拉区3凸形分布，而预制裂隙尖端附近均为受压区，尤其是裂隙R2端周围压应力最大，达到了24 MPa，压应力集中效应最明显。由最大主应力矢量场分析可知，翼裂纹WC-1和WC-2的扩展方向正好与拉应力和压应力的交界面垂直，说明初始翼裂纹是沿着最大的应力降方向扩展。

由图6(b)可知，轴向应力加载至b点(37.35 MPa)时，次生裂纹SC-1出现在预制裂隙R1和R2之间，最终通过不断搭接以弧线的形式连通裂隙R1和R2端，此时，翼裂纹WC-1和WC-4继续扩展，但扩展方向由垂直于裂隙平面变为沿最大加载方向扩展。由图7(b)可知，由于SC-1的出现使受拉区2的拉力得到了释放，靠近裂隙R1和R2端的部分受拉区2转变为受压区，同时，R1和R2端的压应力也得到了释放，然而L1和L2端的压应力集中效应却加强了；由于翼裂纹的继续扩展使 CK-1正上方的受拉区1和CK-2正下方的受拉区3中的部分拉应力释放，出现沿裂纹轨迹的压应力区，使得CK-1正上方的受拉区变为凹形分布，CK-2正下方的受拉区3为凸形分布。由图7(b)还可知：WC-1的下半部分受压状态，从而限制了翼裂纹沿宽度方向扩展，因此，翼裂纹的宽度非常窄，WC-1的上半部分为受拉状态，最大拉应力与最大加载方向垂直，从而使翼裂纹沿最大加载方向扩展，同时，SC-1的出现使WC-2所在的区域变为受压状态，进一步限制了WC-2向裂隙内侧扩展。靠近R2端出现了小部分的受拉区域，可以预测SC-1将在此区域继续扩展。

当轴向应力加载至c点(45.2 MPa)时，结合图6(c)和图7(c)可知，次生裂纹SC-2出现在预制裂隙L1和L2之间，同样以弧线的形式连通L1和L2端，此时裂纹扩展模式与室内试验结果(见图8)基本一致，进一步说明数值模型的合理性。

图8　室内试验结果

Fig. 8　Results of laboratory tests

沿试样45°方向出现了少量的远端微裂纹，WC-1和WC-4继续沿着最大加载方向稳定扩展。SC-2的出现使受拉区2部分区域的拉力再次得到了释放，从而使其扩展路径区域变为受压状态，同时SC-1附近出现了压应力集中的现象，因此，SC-1新萌生的裂纹是在压应力作用下产生的；WC-1和WC-4的扩展再次使受拉区1和3的分布形态发生变化，新裂纹扩展区域的均为受压状态。

由图6(d)和图7(d)可知，随着应变继续增长，轴向应力加载至峰值d点(46.55 MPa)，试样进入全面脆性破坏阶段，次生裂纹SC-2沿45°方向将朝着试样左上方迅速扩展，同时远端的微裂纹继续萌生使原先的拉力场转变为压力场，同时，靠近预制裂隙的受拉区1和3中的拉应力由于翼裂纹的扩展进一步消散，转变为受压区。

图9所示为最大切应力云图。可见，在整个加载的过程中，虽然最大剪应力从26 MPa增加到44 MPa，但其分布并未发生较大的变化，低剪应力主要集中在平行裂隙之间以及CK-1上三角和CK-2下三角区域，高剪应力影响着主要集中在预制裂隙的两侧和裂隙尖端45°方向，影响次生裂纹扩展和最终破坏模式。随着轴向应力增加，低剪应力区域沿着WC-1和WC-4的轨迹上下扩展，高剪应力区域随着次生裂纹的出现缩小的现象。

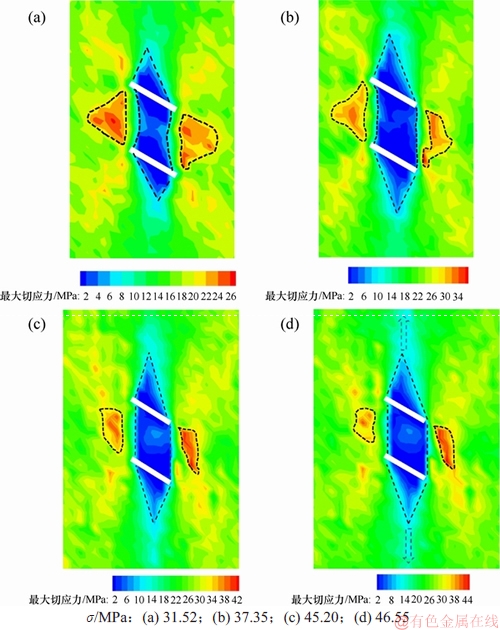
图9　最大切应力演化示意图

Fig. 9　Schematic diagram of maximum shear stress evolution

由数值模型可知，翼裂纹在萌生初期产生的微裂纹数目较少，形成的裂纹宽度较窄，在室内试验中一般无法直接观察到，只有当预制裂隙的R1和R2之间的次生裂纹出现时，应力应变曲线才会出现应力降。翼裂纹在裂隙尖端萌生扩展后将保持较长一段时间不变，颗粒之间的能量不断积聚，直到萌生次生裂纹才释放能量，同时导致平行双裂隙外侧L1和R2端的翼裂纹沿着最大加载方向继续扩展。与翼裂纹在较低轴向应力下萌生不同，次生裂纹一般在峰值前出现，于是试样在轴向应力峰值前积聚的能量过多，平行双裂隙之间的拉应力区域呈“哑铃状”分布，大片区域的拉应力较大，因此次生裂纹一般都是瞬时成片出现，且形成的裂纹的宽度远大于翼裂纹的宽度。次生裂纹的出现导致大片区域的拉应力释放，同时导致相邻附近的压应力场发生变化，从而使次生裂纹继续向裂隙尖端扩展。由于次生出现区域的剪应力和拉压应力都较大，故此时产生的裂纹类型极其复杂，包含张拉微裂纹、拉剪微裂纹和压剪微裂纹。

2.2　位移场演化分析

在颗粒接触发生断裂的过程中，颗粒的位移和运动趋势在一定程度上决定了裂纹的扩展规律和类型，裂纹的不断演化过程在本质上就是颗粒位移的演化过程，因此本文根据裂纹两侧颗粒的位移和相对运动趋势将颗粒的位移场分为类型Ⅰ，Ⅱ，Ⅲ和Ⅳ，具体示意图如图10所示，类型Ⅰ为裂纹两侧颗粒位移水平分量方向相反，竖直分量方向一致，并且位移竖直分量相差不大甚至为0，颗粒的相对运动趋势受位移水平分量控制；类型Ⅱ为裂纹两侧颗粒位移方向相同，数值相差不大，此时颗粒之间的运动趋势在一定程度上抑制了裂纹的萌生扩展；类型Ⅲ为裂纹两侧颗粒位移水平分量和竖直分量方向相同，但大小不同；类型Ⅳ为裂纹两侧颗粒位移方向相反。

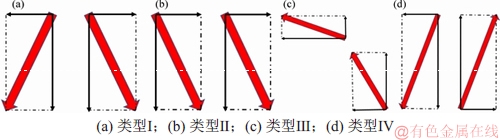
图10　不同类型的颗粒位移场示意图

Fig. 10　Schematic diagram of displacement field for different types of particles

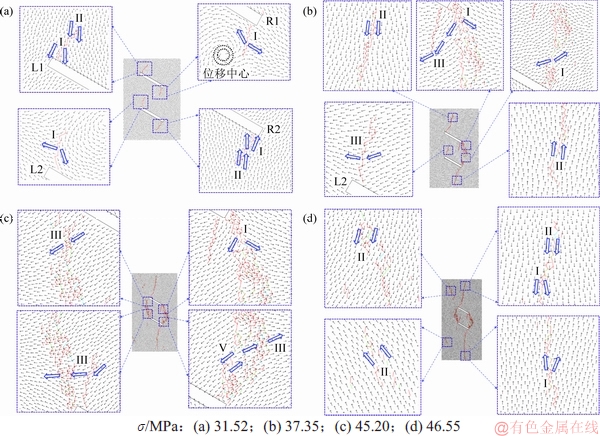
图11　不同加载阶段颗粒位移示意图

Fig.11　Schematic diagram of particle displacement at different loading stages

不同加载阶段颗粒位移示意图如图11所示，其中，小箭头表示颗粒速度，粗箭头表示裂纹附近颗粒的相对运动趋势。裂纹的萌生扩展会导致颗粒的位移场发生显著变化，颗粒之间的相对运动趋势决定着裂纹扩展演化规律。当轴向应力加载至a点(31.52 MPa)时，裂隙尖端萌生翼裂纹，预制裂隙内侧的R1和L2端裂纹两侧的位移类型均为Ⅰ，裂纹两侧区域颗粒的位移方向是反向的，说明此时产生的裂纹为张拉裂纹；预制裂隙外侧的L1和R2端裂纹两侧的位移类型较为复杂，靠近裂隙尖端的位移类型为Ⅰ，远离裂隙尖端的位移类型为Ⅱ，裂纹两侧颗粒的位移方向一致，此部分裂纹是由颗粒之间的相对张拉形成的。当轴向应力加载至b点(37.35 MPa)时，次生裂纹SC-1优先出现在裂隙的右侧，这是由于颗粒大小的随机分布导致在加载过程中试样的位移中心(见图11(a)虚线圆圈)向裂隙右侧偏移，此时SC-1两侧颗粒的位移类型为Ⅰ，说明次生裂纹在初始阶段仍然为张拉裂纹，同时继续扩张的翼裂纹WC-1和WC-4两侧颗粒的位移类型仍然为Ⅱ；L1和R2端裂纹两侧的位移类型演变为Ⅲ，裂纹两侧颗粒水平分量一致，WC-2和WC-3处于压剪状态，在一定程度上抑制了其扩展。

当轴向应力加载至c点(45.20 MPa)时，次生裂纹SC-2两侧的位移类型均为Ⅲ，说明此时萌生的裂纹为拉剪复合型裂纹，同时SC-1继续萌生扩展，使得靠近R2端的裂纹两侧颗粒的位移类型演变为Ⅲ和Ⅴ，新萌生的裂纹为拉剪复合裂纹和剪切裂隙裂纹。随着轴向应力加载至峰值d点(46.55 MPa)，WC-1和WC-2端的翼裂纹继续扩展，其中靠近裂隙的WC-1两侧颗粒的位移类型为Ⅰ，远离裂隙尖端的位移类型为Ⅱ，而WC-1两侧颗粒的位移类型又变为Ⅰ，同时，在远离裂隙区域萌生了远端微裂纹，其位移类型均为Ⅱ，说明此时萌生的微裂纹为拉剪复合裂纹。

3 结论

1) 翼裂纹在最大应力降的作用下沿着垂直裂隙平面方向扩展至一定长度后将保持较长时间不变，直到裂隙尖端R1和R2之间的次生裂纹大量出现后，裂隙外侧的翼裂纹才会在最大拉应力的作用下沿着最大加载方向继续扩展，导致了拉应力区1和3的应力状态发生改变。

2) 次生裂纹包含张拉微裂纹、拉剪微裂纹和压剪微裂纹，次生裂纹萌生时呈现出数量多，时间短的特点，并使WC-2和WC-3处于压剪状态，抑制了其进一步扩展，然而在萌生初期，次生裂纹的出现反而削弱了裂隙尖端的压应力集中效应，从而使次生裂纹继续朝裂隙尖端扩展。在次生裂纹萌生前，裂隙之间的拉应力区域呈“哑铃状”分布，相当一片区域的拉应力较大，因此，次生裂纹一般是瞬时成片出现，且形成的裂纹的宽度远大于翼裂纹的宽度。

3) 在整个加载的过程中，最大剪应力随着轴向应变增加而增加，但其分布并未发生较大的变化，低剪应力主要集中在平行裂隙之间以及CK-1上三角和CK-2下三角区域，高剪应力主要集中在预制裂隙的两侧。

4) 翼裂纹主要是由颗粒之间的相对拉伸或直接拉伸产生，说明翼裂纹为张拉裂纹；次生裂纹萌生机理较为复杂，在萌生初期，由于试样位移中心靠近裂隙的右侧，故SC-1以拉裂纹的形式优先出现在R1和R2之间，随着轴向应力增加，SC-1继续扩展，但萌生的新裂纹却是拉剪复合型裂纹。

参考文献：

[1] BOBET A, EINSTEIN H H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(7): 863-888.

[2] BOBET A. The initiation of secondary cracks in compression[J]. Engineering Fracture Mechanics, 2000, 66(2): 187-219.

[3] ZHAO Y, ZHANG L, WANG W, et al. Cracking and stress-strain behavior of rock-like material containing two flaws under uniaxial compression[J]. Rock Mechanics and Rock Engineering, 2016, 49(7): 2665-2687.

[4] 张晋勋, 杨昊, 单仁亮, 等. 冻结条件下平行双裂隙岩体力学特性试验研究[J]. 岩土力学, 2017, 38(12): 3573-3580, 3589.

ZHANG Jinxun, YANG Hao, SHAN Renliang, et al. Experimental study on mechanical characteristics of two parallel fractured rock under frozen condition[J]. Rock and Soil Mechanics, 2017, 38(12): 3573-3580, 3589.

[5] 黄彦华, 杨圣奇, 鞠杨, 等. 断续裂隙类岩石材料三轴压缩力学特性试验研究[J]. 岩土工程学报, 2016, 38(7): 1212-1220.

HUANG Yanhua, YANG Shengqi, JU Yang, et al. Experimental study on mechanical behavior of rock-like materials containing pre-existing intermittent fissures under triaxial compression[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1212-1220.

[6] CUNDALL P A, STRACK O. A discrete numerical-model for granular assemblies[J]. Geotechnique,1979, 29(1): 47-65.

[7] YANG S, HUANG Y, RANJITH P G, et al. Discrete element modeling on the crack evolution behavior of brittle sandstone containing three fissures under uniaxial compression[J]. Acta Mechanica Sinica, 2015, 31(6): 871-889.

[8] YANG S, TIAN W, HUANG Y, et al. Experimental and discrete element modeling on cracking behavior of sandstone containing a single oval flaw under uniaxial compression[J]. Engineering Fracture Mechanics,2018, 194: 154-174.

[9] 袁康,蒋宇静,李亿民,等.基于颗粒离散元法岩石压缩过程破裂机制宏细观研究[J].中南大学学报(自然科学版),2016,47(3):913-922.

YUAN Kang, JIANG Yujing, LI Yimin, et al. Macro-micro mechanical research on failure mechanism of rock subjected to compression loading based on DEM[J]. Journal of Central South University(Science and Technology), 2016,47(3):913-922.

[10] 胡训健, 卞康, 李鹏程, 等. 含2条断续裂隙试件直接拉伸下的颗粒流模拟[J]. 地质科技情报, 2018, 37(3): 242-247.

HU Xunjian, BIAN Kang, LI Pengcheng, et al. Particle flow analysis of rock with two non-persistent flaw in direct tension[J]. Geological Science and Technology Information, 2018, 37(3): 242-247.

[11] PENG J, WONG L N Y, TEH C I. Effects of grain size-to-particle size ratio on micro-cracking behavior using a bonded-particle grain-based model[J]. International Journal of Rock Mechanics and Mining Sciences. 2017, 100: 207-217.

[12] XIA M, ZHOU K. Particle simulation of the failure process of brittle rock under triaxial compression[J]. International Journal of Minerals Metallurgy and Materials, 2010, 17(5): 507-513.

[13] FAN X, KULATILAKE P H S W, CHEN X, et al. Crack initiation stress and strain of jointed rock containing multi-cracks under uniaxial compressive loading: a particle flow code approach[J]. Journal of Central South University, 2015;22(2):638–645.

[14] 张社荣, 孙博, 王超, 等. 双轴压缩试验下岩石裂纹扩展的离散元分析[J]. 岩石力学与工程学报, 2013,32(S2):3083-3091.

ZHANG Sherong, SUN Bo, WANG Chao, et al. Discrete element analysis of crack propagation in rocks under biaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3083-3091.

[15] 杨庆, 刘元俊. 岩石类材料裂纹扩展贯通的颗粒流模拟[J]. 岩石力学与工程学报, 2012,31(S1): 3123-3129.

YANG Qing, LIU Yuanjun. Simulations of crack propagation in rock-like materials using particle flow code[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3123-3129.

[16] 黄彦华，杨圣奇. 非共面双裂隙红砂岩宏细观力学行为颗粒流模拟[J]. 岩石力学与工程学报, 2014, 33(8): 1644-1653.

HUANG Yanhua, YANG Shengqi. Particle flow simulation of macro- and meso-mechanical behavior of red sandstone containing two pre-existing non-coplanar fissures[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1644-1653.

[17] 邓清海, 巩林贤, 马凤山, 等. 基于颗粒流的直切槽式巴西圆盘裂纹扩展分析[J]. 工程地质学报, 2017, 25(2)：402-409.

DENG Qinghai, GONG Linxian, MA Fengxian, et al. Analysis of crack propagation of crack straight through brazilian disc using particle flow code[J]. Journal of Engineering Geology, 2017, 25(2)：402-409.

[18] ZHANG X P, WONG L N Y. Cracking processes in rock-like material containing a single flaw under uniaxial compression: A numerical study based on parallel bonded-particle model approach[J]. Rock Mechanics and Rock Engineering, 2011, 44(S1): 711-737.

[19] ZHANG X, WONG L N Y. Crack initiation, propagation and coalescence in rock-like material containing two flaws: a numerical study based on bonded-particle model approach[J]. Rock Mechanics and Rock Engineering, 2013, 46(5): 1001-1021.

[20] ZHANG X P, WONG L N Y. Loading rate effects on cracking behavior of flaw-contained specimens under uniaxial compression[J]. International Journal of Fracture, 2013, 180(1): 93-110.

[21] WONG L N Y, EINSTEIN H H. Systematic evaluation of cracking behavior in specimens containing single flaws under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 239-249.

[22] YOON J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871-889.

[23] CHO N, MARTIN C D, SEGO D C. A clumped particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997-1010.

[24] YANG Shengqi, LIU Xiangru, JING Hongwen. Experimental investigation on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 63: 82-92.

[25] Itasca Consulting Group Inc. Users' manual for particle flow code(PFC), version 5.0[R].Minneapolis:Itasca Consulting Group Inc, 2014: 6-30.

(编辑 赵俊)

收稿日期： 2019 -03 -01; 修回日期： 2009 -05 -20

基金项目(Foundation item)：国家自然科学基金资助项目(51879149，51779134，51579142)，山东省泰山学者工程项目(2017) (Projects(51879149，51779134，51579142) supported by the National Natural Science Foundation of China; Project(2017) supported by Taishan Scholars Program of Shandong Province)

通信作者：李勇，副教授，从事岩石力学的物理模拟与数值模拟研究；E-mail: yongli@sdu.edu.cn