挠性航天器快速机动输出反馈控制
唐强,王岩,陈兴林
(哈尔滨工业大学 航天学院,黑龙江 哈尔滨,150001)
摘要:研究挠性航天器在执行快速机动任务时的姿态控制问题。针对既要满足快速性,又要抑制航天器挠性附件振动的要求,提出一种具有普遍性意义的基于无源性的输出反馈控制方法。并采用Lyapunov方法从理论上分析和证明了闭环系统的渐近稳定性。最后针对地观测卫星进行大角度快速机动进行了仿真验证。研究结果表明:所设计的方法不仅能够有效地抑制挠性振动,而且满足快速机动的要求。
关键词:挠性航天器;快速机动;输出反馈;无源性
中图分类号:V448.2 文献标志码:A 文章编号:1672-7207(2011)S1-0309-05
Fast maneuver output feedback control for flexible spacecraft
TANG Qiang, WANG Yan, CHEN Xing-lin
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
Abstract: The output feedback control problem for flexible spacecraft fast maneuver was investigated. A more general passivity-based control law was proposed to meet the requirements of rapidity and vibration suppression. Then the Lyapunov method was used to analysis and proves asymptotic stability of the closed loop system. Simulation results of earth observation satellite during large angle rapid maneuvering show the effectiveness of the proposed control schemes.
Key words: flexible spacecraft; fast maneuver; output feedback; passivity
随着航天技术日新月异的发展,航天器的空间结构日趋复杂,并且广泛采用轻质结构,使得航天器主体上的挠性附件越来越多。由于其本身具有质量小、挠性大、阻尼弱的特点,易激起低频、非线性、大幅度的振动,且与航天器主体的姿态运动耦合,严重影响航天器姿态控制系统的正常工作,因此,对航天器的机动性和姿态控制精度提出了更高的要求。对地观测卫星就属于典型的复杂的大型空间结构,承载着大型载荷、大面积的帆板、大量液体燃料和多个运动部件。由于观测的需要,要求卫星经常性的俯仰机动和侧摆机动,此时星上的挠性附件对卫星大角度快速机动和快速稳定产生严重的影响,因此,在姿态控制器设计时必须考虑如太阳帆板和天线等挠性部件的振动。可见,研究挠性航天器快速稳定问题具有重要的工程价值和理论意义。国内外对挠性航天器姿态控制问题进行了广泛研究。Gavallo等[1]应用H无穷鲁棒控制方法解决挠性结构在参数不确定情况下的振动问题。Fei[2]分别采用最小二乘自适应控制和自适应变结构控制来抑制挠性梁的振动。Gennaro[3]利用无源性方法设计了四元数反馈渐近稳定控制器,解决了挠性航天器的姿态跟踪问题。Zheng等[4]根据最优控制理论,设计了时变LQR控制器实现了三轴稳定挠性航天器的姿态控制。Gennaro[5]研究了干扰情况下挠性航天器姿态的非线性控制问题。Dharne等[6]通过自适应控制和输入成型相结合的方法,成功应用于振动频率不确定情况下的挠性航天器的大角度机动。在此,本文作者针对挠性航天器进行大角度机动时的快速稳定问题,提出一种具有普遍性意义的无源性输出反馈控制方法,提高了控制器选择的多样性和针对性。首先描述了挠性航天器动力学方程,采用四元数描述系统的运动学方程,设计了一种基于姿态四元数和角速度反馈的全局渐近稳定控制律,并采用Lyapunov方法证明了系统的全局收敛性。最后通过数字仿真验证了该方法的理论正确性和实用性。
1 挠性航天器数学模型
考虑由刚体和挠性附件组成的航天器系统,其动力学方程为[3]
 (1a)
(1a)
 (1b)
(1b)
式中: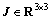 ,为挠性航天器的转动惯量矩阵;
,为挠性航天器的转动惯量矩阵; 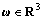 ,为挠性航天器在本体坐标系下相对惯性坐标系的姿态角速度;
,为挠性航天器在本体坐标系下相对惯性坐标系的姿态角速度;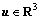 ,为挠性航天器控制力矩,对于向量
,为挠性航天器控制力矩,对于向量 ,
,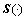 为向量积矩阵:
为向量积矩阵:
 (2)
(2)
η为广义模态坐标,δ为刚挠耦合系数矩阵,C和K分别为阻尼和刚度矩阵,ξ为挠性附件振动阻尼比,ωni为挠性附件振动模态频率。
 ,
,
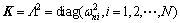 。
。
令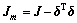 ,表示挠性航天器主体部分的转动惯量矩阵,
,表示挠性航天器主体部分的转动惯量矩阵,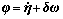 表示挠性体部分的速度,那么,挠性航天器的动力学模型可以进一步简化为:
表示挠性体部分的速度,那么,挠性航天器的动力学模型可以进一步简化为:
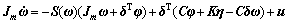 (3a)
(3a)
 (3b)
(3b)
为了避免姿态角出现奇异值,本文采用四元数 描述系统的运动学方程[7]:
描述系统的运动学方程[7]:
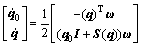 (4)
(4)
其中四元数满足条件 。
。
2 输出反馈控制律设计
为了满足系统大角度机动时快速稳定的要求,根据无源性控制器设计准则,受文献[8]的启发提出如下控制器:
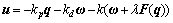 (5)
(5)
定理 1 针对式(3)和(4)所描述的挠性航天器系统,存在常数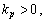
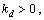
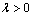 ,若采用式(5)所示的控制器能够保证闭环系统的全局渐近稳定性,并有如下结论成立:
,若采用式(5)所示的控制器能够保证闭环系统的全局渐近稳定性,并有如下结论成立:
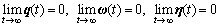
证明:
根据系统特性选取Lyapunov函数:
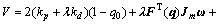
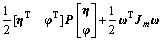
式中:F(q)是q的函数,并且满足如下条件: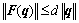 即
即 。
。
转动惯量Jm满足不等式:
 ,其中σmax和σmin分别表示矩阵的最大和最小奇异值。因此,V可以简化为:
,其中σmax和σmin分别表示矩阵的最大和最小奇异值。因此,V可以简化为:
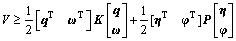
式中: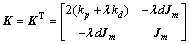
矩阵P是下面方程的解:
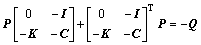
其中: ,根据Schur补定理,当λ取足够小的时候可以保证矩阵K的正定性。
,根据Schur补定理,当λ取足够小的时候可以保证矩阵K的正定性。
为了方便化简令 。沿着系统(式(3))解的轨迹,V对时间求导可得:
。沿着系统(式(3))解的轨迹,V对时间求导可得:
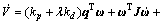
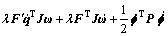 (6)
(6)
将式(3)代入式(6)可得:
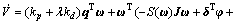
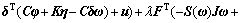
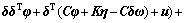
 (7)
(7)
进一步将式(5)代入式(7)可得:
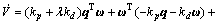
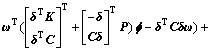
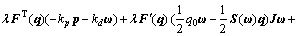
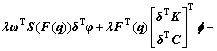
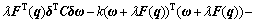
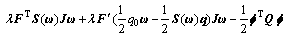
令 ,并且引入辅助变量v:
,并且引入辅助变量v:
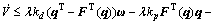
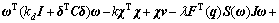
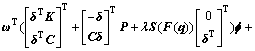
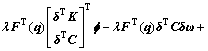
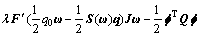
假设函数F(q)满足如下条件:在定义区间内,F′(q)连续有界,即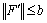 ,
, ,而且
,而且 ,
,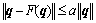 ,
, ,
, ,
,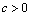 ,
, ,ω满足条件
,ω满足条件 。
。 进一步简化为:
进一步简化为:
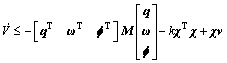 (8)
(8)
其中:
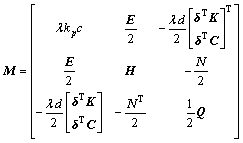
式中:
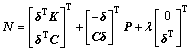
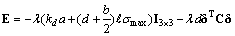
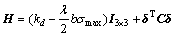
因此,只要选取合适的λ,kp和kd,就能够保证矩阵M的正定性。由式(8)可知: ,表明从输入v到输出χ的闭环系统是无源的。根据系统无源性与渐近稳定性的关系可以得知:当
,表明从输入v到输出χ的闭环系统是无源的。根据系统无源性与渐近稳定性的关系可以得知:当 时,有
时,有 ,
, ,
, ,所以,闭环系统是渐近稳定的。从上面的证明可以看出函数F(q)只要满足以下的条件:
,所以,闭环系统是渐近稳定的。从上面的证明可以看出函数F(q)只要满足以下的条件:
(1) F(q)连续可导并且 ;
;
(2) F(q)的导数连续并且有界。
就可以保证系统的渐近稳定性,由于这样的函数很多,可以根据实际控制系统的需要来选择合适的函数,比如与最优控制理论相结合(时间最短,收敛速度最快等)来选择函数,因此,给控制器的设计提供更多的选择。根据一般性的原则可以选取F(q)=q,考虑到系统快速机动和快速稳定的要求本文采用双曲正切函数F(q)=tanh(βq)(β>0)。
3 仿真算例
本文将所设计的控制器用于对地观测卫星的大角度快速机动的仿真验证。主要参数选取为[9]:
 ,
,
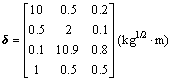
模型中采用四阶挠性模态,其中,
 ,
,
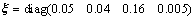 。
。
控制参数选取kp=2 000,kd=6 000,λ=5,β=20。 为挠性航天器初始姿态。挠性航天器初始姿态角速度
为挠性航天器初始姿态。挠性航天器初始姿态角速度 ,仿真中执行机构采用10 N·m的控制力矩陀螺,采样时间为0.01 s,仿真时间为60 s。仿真结果如图1~5所示。
,仿真中执行机构采用10 N·m的控制力矩陀螺,采样时间为0.01 s,仿真时间为60 s。仿真结果如图1~5所示。
从图1和图2可以看出:角速度和姿态四元数快速收敛于平衡点。图4表明姿态角准确平滑的执行了机动指令。图5表明模态振动得到了有效抑制。综上所述,本文所提出的控制器能有效保证挠性航天器快速机动时,达到姿态控制快速性和稳定性期望的要求。
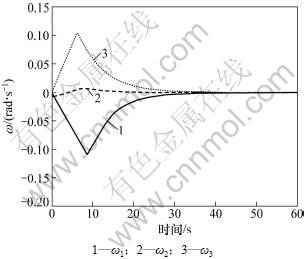
图1 角速度ω响应曲线
Fig.1 Response curves of angular rate
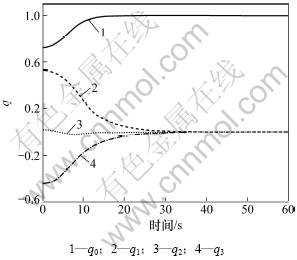
图2 四元数Q变化曲线
Fig.2 Response curves of unit-quaternion
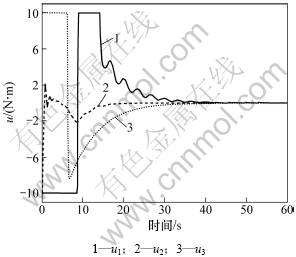
图3 控制量变化曲线
Fig.3 Profile curves of control law
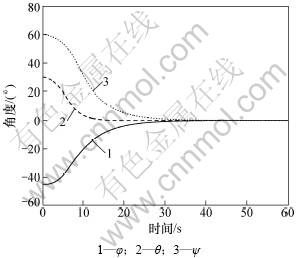
图4 姿态角变化曲线
Fig.4 Response curves of angle
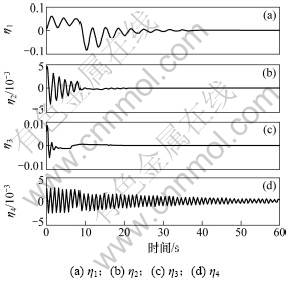
图5 振动模态η变化曲线
Fig.5 Response curves of vibration mode
4 结论
本文针对挠性航天器大角度机动的姿态控制问题,提出了一种具有普遍性意义的基于无源性的控制方法。该方法通过姿态四元数和姿态角速度来实现输出反馈控制,同时采用姿态四元数的非线性函数来提高系统的快速收敛性。由于非线性函数选择的多样性,提高了控制器设计的选择余地,因此,能够更好地适应系统本身的特性。此外,该方法还具有结构简单,易于实现的特点。仿真结果验证了控制器理论设计的正确性和方法的可行性。
参考文献:
[1] Cavallo A, de Maria G, Natale C. Robust control of flexible structures stable bandpass controllers[J]. Automatica, 2008, 44(5): 1251-1260.
[2] Fei J. Adaptive sliding mode vibration control schemes for flexible structure system[C]//The 46th IEEE Conference on Decision and Control, 2007. New Orleans, Louisiana: IEEE, 2007: 1332-1337.
[3] di Gennaro D. Passive attitude control of flexible spacecraft from quaternion measurements[J]. Journal of Optimization Theory and Applications, 2003, 116(1): 41-60.
[4] Zheng J H, Banks S P, Alleyne H. Optimal attitude control for three-axis stabilized flexible spacecraft[J]. Acta Astronautica, 2005, 56(5): 519-528.
[5] di Gennaro S. Tracking control using attitude measurements for flexible spacecraft in presence of disturbances[C]//The 43rd IEEE Conference on Decision and Control 2004. Paradise Island, Bahamas: IEEE, 2004: 2123-2128.
[6] Dharne A, Jayasuriya S. Robust adaptive control of residual vibration in point-to-point motion of flexible bodies[J]. Journal of Vibration and Control, 2007, 13(7): 951-968.
[7] Shuter M D. A survey of attitude representations[J]. Journal of the Astronautical Sciences, 1993, 41(4): 439-517.
[8] Horri N, Palmer P, Roberts M. Optimal satellite attitude control: A geometric approach[C]//Aerospace Conference 2009. Big Sky, Montana: IEEE, 2009: 1-11.
[9] di Gennaro S. Adaptive robust tracking for flexible spacecraft in presence of disturbances[J]. Journal of Optimization Theory and Applications, 1998, 98(3): 545-568.
(编辑 杨幼平)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金重点资助项目(60535010)
通信作者:唐强(1981-),男,四川营山人,博士研究生,从事姿态控制、精密伺服控制研究;电话:15811248380;E-mail:plutut@126.com