常功率平面热源法测试耐火材料热物性的研究
周孑民,朱再兴,谢东江,李浩,陈伟,张永星
(中南大学 能源科学与工程学院,湖南 长沙,410083)
摘要:在对常功率平面热源法基本原理深入分析的基础上,根据其在第二类边界条件下半无限大物体一维导热的数学模型,研制一套低导热系数材料的热物性测量装置,并结合相关文献通过数值计算获得高斯误差补函数一次积分较为精确的解。设计的测试系统采用数据采集卡DUT5000,利用VB编程技术对温度进行实时采集及处理,测定8种耐火砖和陶瓷纤维的导热系数和导温系数。研究结果表明,本研究所设计的测试系统所得导热系数和导温系数与文献中的结果相对误差不超过6%,具有结构简单、操作方便、测试时间短、精度较高等特点。
关键词:导热系数;导温系数;常功率平面热源法;误差分析;数值计算
中图分类号:O551.3 文献标志码:A 文章编号:1672-7207(2011)05-1467-06
Thermal physical property of refractory material measured by plane heat source method with constant heat rate
ZHOU Jie-min, ZHU Zai-xing, XIE Dong-jiang, LI Hao, CHEN Wei, ZHANG Yong-xing
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Based on the principle of constant heat rate source method and one-dimensional conduction mathematic model for semi-infinite object built under the second boundary condition, a set of device for measuring materials with low thermal conductivity was developed and precise analytical solution was obtained by numeric calculation in related references. The DUT5000 data acquisition card and VB software were used to conduct real-time data acquisition and data processing. The thermal diffusivity and thermal conductivity of eight kinds of firebricks and ceramic fibers were tested. The results show that the relative errors between experimental results and results from references are evaluated to be within 6%. The testing system has the characteristic of simple structure, easy operation, short testing time and high precision.
Key words: thermal conductivity; thermal diffusivity; plane heat source method with constant heat rate; error analysis; numeric calculation
随着能源问题的突出和能源科学的发展,热物性学的研究越来越受到重视,热物性学中物质热物性参数的确定也就显得尤为重要。常功率平面热源法作为一种经典的热物性测试方法,具有测试时间短、测试原理简单等优点[1-2]。常功率平面热源法于20世纪70年代由天津大学物理工程系提出,王补宣等[3]对测试误差的控制进行了研究,将常功率平面热源法的累积误差(包括方法误差、仪器误差和测量误差)控制在6%以内。崔萍等[4]对传统的常功率平面热源法进行了研究,建立了改进的数学模型,提出了新的数据处理方法。本文作者根据常功率平面热源法的原理,利用现代先进的数据采集及计算机技术[5-6],自行设计了一套低导热系数材料的导温系数、导热系数测量装置,对耐火材料和保温材料的导热系数进行测量。
1 理论分析
常功率平面热源法所依据的半无限大物体一维导热的数学模型及坐标如图1所示。
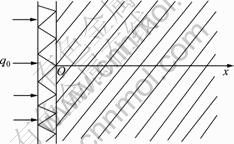
图1 数学模型及坐标
Fig.1 Mathematical model and coordinate
在初始温度ti分布均匀的半无限大物体的表面(x=0)上,受均匀分布的平面热源作用,热流密度为q0,在常物性假设条件下,距表面x处,τ时刻的温升 为[7-8]:
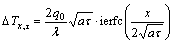 (1)
(1)
式中: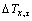 为温升,
为温升,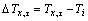 ,K;
,K;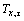 为τ时刻的温度,K;q0为热流密度,W?m-2;λ为导热系数,W?(m?K)-1;a为导温系数,m2?s-1;τ为时间,s;ierfc( )为高斯误差补函数的一次积分。
为τ时刻的温度,K;q0为热流密度,W?m-2;λ为导热系数,W?(m?K)-1;a为导温系数,m2?s-1;τ为时间,s;ierfc( )为高斯误差补函数的一次积分。
当τ=τ0,x=0时,
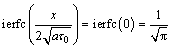
则
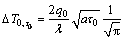 (2)
(2)
当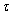 =
=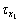 ,x=x1时,
,x=x1时,
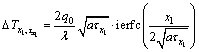 (3)
(3)
用式(3)除以式(2)可得
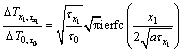 (4)
(4)
若令
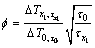 (5)
(5)
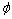 是在实验中可以测出来的量,由它可以求出以下值:
是在实验中可以测出来的量,由它可以求出以下值:
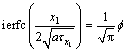 (6)
(6)
若能根据式(6)求出自变量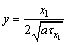 ,则平均温度
,则平均温度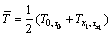 的导温系数为:
的导温系数为:
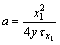 (7)
(7)
将式(7)代入式(2),即可求出试材的导热系数λ:
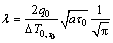 (8)
(8)
以往常用的方法是测出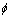 ,根据式(6)查表确定自变量
,根据式(6)查表确定自变量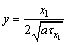 ,本文则根据参考文献[9]介绍的方法采用数值计算确定其值。
,本文则根据参考文献[9]介绍的方法采用数值计算确定其值。
根据参考文献[9]:
 (9)
(9)
式中:erfc( )为高斯误差补函数。
将式(9)代入式(6)可得:
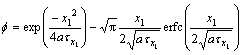 (10)
(10)
令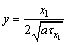 ,则
,则
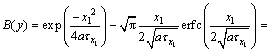
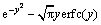 (11)
(11)
式中:
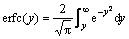 (12)
(12)
将式(12)代入式(11)得:
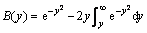 (13)
(13)
显然,B(y)即为测定的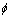 。将得到的
。将得到的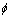 代入式(13),并写成:
代入式(13),并写成:
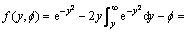
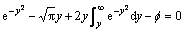 (14)
(14)
运用Newton迭代法计算y,则有
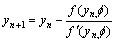 ;n=0, 1, 2, … (15)
;n=0, 1, 2, … (15)
式中:n为迭代次数。将指数函数作级数展开:
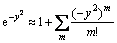 (16)
(16)
取其前m项,经积分得:
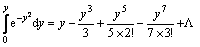 (17)
(17)
同时,对这个积分式进行一次微分,有:
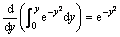 (18)
(18)
因此,利用式(16),(17)及(18)可计算函数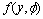 和该函数对y的一阶导数
和该函数对y的一阶导数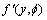 。将
。将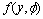 和
和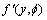 代入式(15),经化简整理,利用VB来编程计算可以算出y或y2。增加取项数m和迭代次数n,可以按需要提高计算的准确度。
代入式(15),经化简整理,利用VB来编程计算可以算出y或y2。增加取项数m和迭代次数n,可以按需要提高计算的准确度。
2 测试装置
测试装置如图2所示,从下至上的3个热电偶所处的位置分别为测温点1,2和3。若试样的长和宽各为其厚度的8~10倍,加热器的功率恒定,热容量可
忽略,并且试样无内热源,则试样Ⅰ可看作是“大平壁”[10-11]。由加热器通电加热时,试样Ⅰ的2个表面中央区域都在整个升温过程中保持等温面。随着加热时间的延长,τ>0,试样紧挨加热器的部分首先开始升温,并逐步向远离加热其的两边延伸,直到τ= 时,试样Ⅱ的上表面和试样Ⅲ下表面也将开始升 温。在0<τ<
时,试样Ⅱ的上表面和试样Ⅲ下表面也将开始升 温。在0<τ< 期间,试样Ⅰ和Ⅱ迭接在一起,试样Ⅰ和Ⅱ以及试样Ⅲ将表现为2个事实上的半无限大物体。由于试样Ⅰ加上试样Ⅱ的厚度与试样Ⅲ的厚度相等,因此,加热器也将均等地向两侧供热,从而解决了加热热流密度难确定的问题。
期间,试样Ⅰ和Ⅱ迭接在一起,试样Ⅰ和Ⅱ以及试样Ⅲ将表现为2个事实上的半无限大物体。由于试样Ⅰ加上试样Ⅱ的厚度与试样Ⅲ的厚度相等,因此,加热器也将均等地向两侧供热,从而解决了加热热流密度难确定的问题。
分别对黏土和石棉设置保温层和不设保温层2种情况进行测试,验证试样四周对流散热对测试结果的影响,保温材料为石棉,保温层厚6 cm;对硅藻土耐火砖和灰砂砖在不同热流密度下进行测试;对硅砖、黏土砖、硅藻土耐火砖等8种材料进行非稳态法(常功率平面热源法)和稳态法(平板法)测试。由于本实验的试样具有低导热系数的特点,而且试样很薄,成为长和宽各为其厚度的8~10倍的无限大平板,从而能在试样中产生一个均匀的一维热流[12-13],经过足够长的加热时间后,当测温点1和2的温度不再上升时,便满足了平板法的测试条件,故可利用本装置根据平板法的测试原理测试材料的导热系数。这也是本研究的一个特点:利用本装置能同时实现常功率平面热源法和平板法对材料的导热系数进行测试,兼顾了常功率平面热源法和平板法的优点。
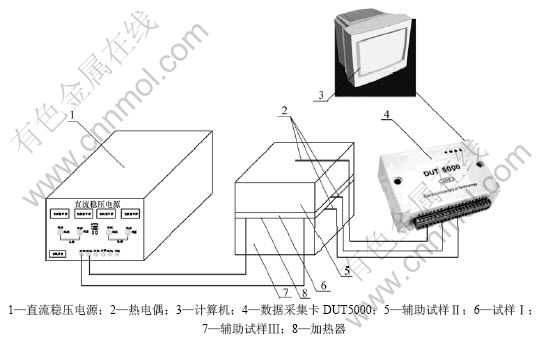
图2 测试系统装置简图
Fig.2 Diagram of testing system
3 试验结果分析
3.1 试样四周散热对测试结果的影响
图3所示为保温层对黏土升温曲线的影响,图4所示为保温层对石棉升温曲线的影响,表1所示为试样四周设置保温层和不设保温层时所测导热系数。从图3、图4和表1可以看出,一方面,在试样四周设置保温层和不设保温层时,黏土和石棉的测温点1和2的升温曲线均较吻合,温度随时间的变化趋势可以认为是一致的;另一方面,试样四周不设保温层时测
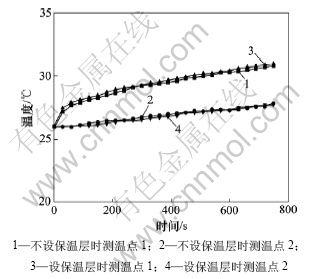
图3 保温层对黏土升温曲线的影响
Fig.3 Influence of insulation layer on temperature change curves for clay

图4 保温层对石棉升温曲线的影响
Fig.4 Influence of insulation layer on temperature change curves for asbestos
表1 试样四周设置保温层和不设保温层时所测导热系数的比较
Table 1 Comparison of measuring thermal conductivity with and without insulation layer set around specimen
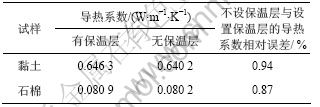
得的导热系数与设置保温层时测得的导热系数相对误差不超过1.0%,故在精度要求不是很高时,可以认为这2种情况下测得的导热系数差别很小,加与不加保温层对实验结果影响非常小。从而说明了当试样的长和宽都为其厚度的8~10倍时,试样中的导热属于一维非稳态导热,试样四周的对流散热可以忽略。因此,试验时,没有必要在试样的四周设置保温层,达到简化了实验装置的目的。
3.2 热流密度对测试结果的影响
图5和图6所示分别为硅藻土耐火砖在热流密度为191.8和378.8 W/m2及灰砂砖在热流密度为99.8和197.3 W/m2的测试曲线。从图5和6可以看出:加热器通电后的初始阶段,测温点1的温度迅速升高,此时,测温点2的温度几乎没有变化,曲线平稳,这是因为热量还未传递到试样Ⅰ的上表面。约100 s后,测温点1的温度持续上升,测温点2的温度也出现较大的上升趋势;在测试结束前的最后阶段,测温点1和测温点2的温度上升比较缓慢。整个测试过程中,测温点1 的温度始终高于测温点2 的温度。结合图5 和
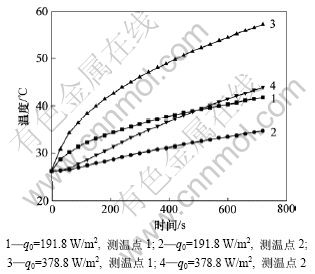
图5 硅藻土耐火砖在不同热流密度下的升温曲线
Fig.5 Temperature change curves for diatomite firebrick under different heat fluxes
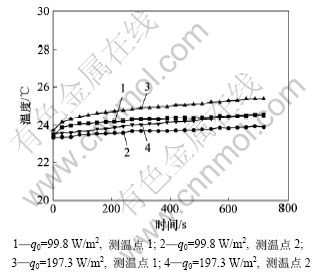
图6 灰砂砖在不同热流密度下的升温曲线
Fig.6 Temperature change curves for lime-sand brick under different heat flux
图6还可以看出:当加热热流密度增大时,温度上升的速率也增大;加热热流密度越大,温度上升得越快。
3.3 不同材料实验分析
图7所示为硅砖和石棉在热流密度均为162.7 W/m2的升温曲线。从图7可以看出,加热后石棉的测温点1的温度迅速上升,一段时间后测温点2的温度也开始上升,约300 s后,石棉的测温点2的温度比硅砖的测温点1的温度还高,石棉测温点1和2的温差大;而硅砖的测温点1和2的温度在整个加热过程中均上升得比较缓慢,并且两者的温差比较小,由表2可以看出:石棉的导热系数为0.080 2 W/(m?K),硅砖的导热系数为1.051 0 W/(m?K),石棉的导热系数比硅砖的要小得多,因此,在相同的热流密度下,导热系
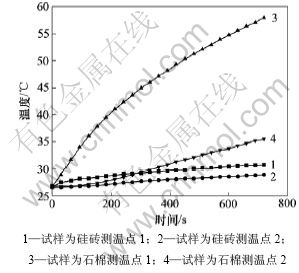
图7 不同材料的升温曲线的比较
Fig.7 Comparison of temperature change curves for different materials
数小的材料其温度上升得快。这是因为由式(8)可得: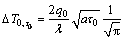 ,当热流密度q0和τ0一定时,试样中某点的温升与导热系数成反比,故材料的导热系数越小,温升越大,温度上升得越快;反之,导热系数越大,温升越小,温度上升得越慢。本装置只适合对低导热系数的材料(如保温材料和耐火材料等)进行测量。
,当热流密度q0和τ0一定时,试样中某点的温升与导热系数成反比,故材料的导热系数越小,温升越大,温度上升得越快;反之,导热系数越大,温升越小,温度上升得越慢。本装置只适合对低导热系数的材料(如保温材料和耐火材料等)进行测量。
3.4 多种材料综合误差
试验对硅砖、黏土保温砖、硅藻土耐火砖等8种材料分别进行了3组常功率平面热源法实验和1组平板法实验,其测试结果和文献值的比较见表2。 由于不知道文献值是在何种条件下测出的,而稳态法测得
表2 8种材料测试结果综合分析
Table 2 Comprehensive analysis of experimental results of eight materials
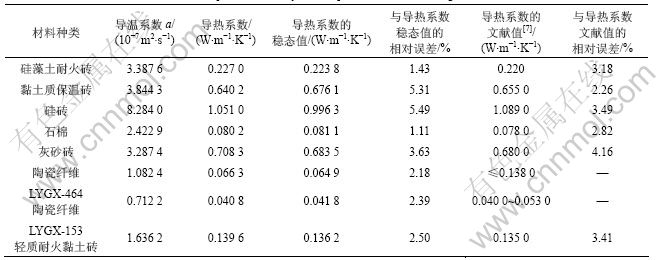
的材料的导热系数要比非稳态法测得的准确些[14],因此,有必要将测得的结果和稳态法得到的结果进行 比较。
4 结论
(1) 试样边缘散热对测试结果影响比较小,可以忽略试样四周的散热,其导热模型属一维导热问题(只在试样的厚度方向有热量的传递,长、宽方向均无热量的传递)。因此,测试导热系数较低的材料时没有必要在试样边缘设置绝热保护层,这使测试系统更加 简单。
(2) 本测试系统既具有常功率平面热源法测试周期短且能同时测出材料导温系数和导热系数的优点,又具有平板法测试准确度高、误差小的优点。
(3) 当材料的导热系数大到一定值后,用本实验装置测试时,其温度上升很慢,温差非常小。本装置只适合对低导热系数的材料进行测量;测试的8种低导热系数材料的导温系数和导热系数与文献参考值及稳态法测得值较吻合,相对误差在6%以内。因此,该测试方法用于测试导热系数较低的材料时,所得导热系数具有较高的测试精度。
参考文献:
[1] 王补宣, 任泽霖, 方肇洪. 利用双平板导热仪测定导热系数的测试技术和误差分析[J]. 工程热物理学报, 1982, 3(1): 1-2.
WANG Bu-xuan, REN Ze-lin, FANG Zhao-hong. Measuring technology and error analysis on the measurement of thermal conductivity using two-plane thermal conductivity instrument[J]. Journal of Engineering Thermophysics, 1982, 3(1): 1-2.
[2] Fukuyo K. Finite analytic method based on power series expansion for unsteady heat conduction problems[J]. Numerical Heat Transfer, 2004, 45(4): 369-384.
[3] 王补宣, 韩礼钟, 王维城, 等. 同时测定绝热材料α和λ的常功率平面热源法[J]. 工程热物理学报, 1980, 1(1): 80-87.
WANG Bu-xuan, HAN Li-zhong, WANG Wei-cheng, et al. A plane heat source method for simultaneous measurement of the thermal diffusivity α and conductibity λ of insulating materials with constant heat rate[J]. Journal of Engineering Thermophysics, 1980, 1(1): 80-87.
[4] 崔萍, 方肇洪. 改进的常功率平面热源法[J]. 山东建筑工程学院学报, 2001, 16(2): 48-52.
CUI Ping, FANG Zhao-hong. Improvement on the plane-source method with constant heating rate on the boundary[J]. Journal of Shandong Institute of Architecture and Engineering, 2001, 16(2): 48-52.
[5] 禹国强, 刘安伟, 张国君, 等. 恒功率平面热源法智能热物理参数测试系统[J]. 仪器仪表学报, 2000, 21(1): 98-103.
Yu Guo-qiang, Liu An-wei, Zhang Guo-jun, et al. An intelligent measuring system for thermal physical properties by plane heat source method with constant heat rate[J]. Chinese Journal of Scientific Instrument, 2000, 21(1): 98-103.
[6] 王长宏, 周孑民, Lamvik M, 等. 周期热流法测定金属材料热物性的实验及数值研究[J]. 长沙电力学院学报:自然科学版, 2005, 20(3): 1-2.
WANG Chang-hong, ZHOU Jie-min, Lamvik M, et al. Numerical and experimental study on the measurement of thermophysical property of metals using periodic heating method[J]. Journal of Changsha University of Electric Power: Natural Science, 2005, 20(3): 1-2.
[7] 陈则韶, 葛新石, 顾毓沁. 量热技术和热物性测定[M]. 合肥: 中国科学技术大学出版社, 1990: 87-99.
CHEN Ze-shao, GE Xin-shi, GU Yu-qin. Calorimetric technology and measurement of thermophysical property[M]. Hefei: University of Science and Technology of China Press, 1990: 87-99.
[8] 涂颉, 章熙明, 李汉炎, 等. 热工实验基础[M]. 北京: 高等教育出版社, 1986: 267-324.
TU Xie, ZHANG Xi-ming, LI Han-yan, et al. Experiment foundation of thermodynamic[M]. Beijing: Higher Education Press, 1986: 267-324.
[9] 陈昭栋, 舒维芬, 邝向军. 热导率瞬态测量的数据处理[J]. 物理实验, 2000, 20(3): 6-8.
CHEN Zhao-dong, SHU Wei-fen, KUANG Xiang-jun. The data processingof transient measurement of thermal conductivity[J]. Physics Experimentation, 2000, 20(3): 6-8.
[10] Kakac S, Yener Y. Heat conduction[M]. Washington: Hemisphere Publishing Corporation, 1986: 109-302.
[11] 薛正华. 周期热流法测定金属及合金导热系数的研究[D]. 长沙: 中南大学能源科学与工程学院, 2004: 1-2.
XUE Zheng-hua. Study on the measurement of thermal conductivity of metals and alloys using periodic heating method[D]. Changsha: Central South University. School of Energy Science and Engineering, 2004: 1-2.
[12] 陈昭栋. 平面热源法瞬态测量材料热物性的研究[J]. 电子科技大学学报, 2004, 33(5): 551-554.
CHEN Zhao-dong, Investigation of transient measurement thermal physics properties by plain thermal source method[J]. Journal of University of Electronic Science and Technology of China, 2004, 33(5): 551-554.
[13] Incropera F P, DeWitt D P. Introduction to heat transfer[M]. New York: John Wiley & Sons, 1996: 212-236.
[14] 陈昭栋, 舒维芬, 陈丕, 等. 在瞬态自动测量仪上用脉冲法测量材料的热物理系数[J].物理实验, 2002, 22(10): 3-5.
CHEN Zhao-dong, SHU Wei-fen, CHEN Pi, et al. Thermal physics coefficient measurement by pulse method with transient automatic measurement apparatus[J]. Physics Experimentation, 2002, 22(10): 3-5.
(编辑 赵俊)
收稿日期:2010-01-14;修回日期:2010-04-20
基金项目:国家自然科学基金资助项目(50876116)
通信作者:周孑民(1948-),男,山东济南人,教授,博士生导师,从事热物性测试及热工设备系统仿真与优化的研究;电话:13974870895;E-mail: jmzhou@csu.edu.cn