DOI：10.19476/j.ysxb.1004.0609.2018.04.11

Inconel625高温合金J-C本构建模

刘二亮，邢宏伟，王明明，徐志超，赵  娜

(哈尔滨理工大学 机械动力工程学院，哈尔滨 150080)

摘  要：为了研究Inconel625高温合金在较高温度和应变率变化范围内的热变形行为，采用CSS电子万能试验机和分离式霍普金森压杆试验装置对Inconel625高温合金进行准静态试验和霍普金森压杆试验，在温度为20~800 ℃、应变率为0.001~8000 s^-1范围内得到Inconel625高温合金的真实应力—应变曲线。结果表明：随着温度的升高，Inconel625高温合金的流动应力与屈服应力并不单一地随应变率增大而增大，同一温度条件下，随着应变率的增加，Inconel625高温合金的真实应力先增大后减小(分界线是应变率为6000 s^-1)；同一应变率条件下，Inconel625高温合金的真实应力随着温度的升高而减小。基于Johnson-Cook模型对其真实应力-应变曲线进行拟合分析，经过计算得到模型的预测值与实验值的相关性和绝对误差，并进一步改进Inconel625高温合金的Johnson-Cook本构模型，使模型能够更好地反映Inconel625高温合金在较高温度和应变率变化范围内的热变形规律。

关键词：Inconel 625高温合金；Johnson-Cook本构模型；应变；热变形

文章编号：1004-0609(2018)-04-0732-10　　     中图分类号：TG501.1　　     文献标志码：A

Inconel625高温合金是一种典型的镍基变形高温合金，该合金中的Cr、Mo、Nb含量高，固溶强化作用强烈，以其高强度、高韧性以及优良的抗疲劳性能被广泛应用于石油、造船、核电工业、航空航天和化工等行业^[1-4]。由于Inconel625高温合金在切削过程中不易散热，极易产生热量堆积，使刀具磨损严重，切削加工性能差。因此，研究其切削热变形规律具有十分重要的意义。

本构方程作为研究切削过程中材料热变形规律的一个重要的数学模型，能够表征材料的塑性流变特征，有效地预测材料的稳态流动应力，为切削过程有限元仿真提供理论依据。目前，国内外学者对材料的本构方程进行了大量的研究。研究人员在应变率为3×10^-4~1 s^-1、温度为950~1150 ℃范围内对Ni-Cr-Co基高温合金进行了热压缩试验，得到了材料的双曲正弦本构模型^[5-7]。魏洪亮等^[8]利用准静态拉伸、对称循环和非对称循环试验研究高温合金GH4169的本构关系，使用非线性优化算法修正了该材料的Choboche本构模型^[9-12]。研究人员开发了一种高温霍杆试验装置^[13-14]，对Ti6Al4V合金从室温到1000 ℃，应变率1400 s^-1范围内的压缩试验，通过试验结果得出了Ti6Al4V合金的修正的Johnson-Cook本构方程，修正后的Johnson-Cook本构方程更适合表达该钛合金的再结晶温度附近的动态行为^[15-16]。李淼泉等^[17]应用模糊神经网络的方法，引用Z-H参数，建立了高温合金GH4169在应变率为0.1~50 s^-1和温度为1203~1323 K范围内的Arrhenius本构模型。宋迎东等^[18]对粉末高温合金FGH95的黏-塑性力学行为进行了研究，并以此为基础建立了粉末高温合金的Bonder-Partom统一弹-黏塑性本构模型。研究人员对Inconel625高温合金在高温段的热变形行为也做了相关研究，并归纳出了该合金在高温段变形的Arrhenius型本构方程^[19-22]。此外，俞秋景等^[23]对Inconel625高温合金在高温、低应变率条件下的热变形行为做了研究，归纳出了该合金在这种条件下的Johnson-Cook本构模型。然而，上述研究大多局限于较窄的温度范围和较低的应变率条件下^[24-25]，而切削是在一个高温和应变率变化十分复杂的环境下进行的过程，因此上述模型不能够有效描述材料在切削过程中的热变形行为。Johnson-Cook本构模型以其参数简单、准确率高以及更加接近切削实际的特点被广泛应用于切削有限元仿真中^[26-27]。因此，建立一种在高温以及应变率变化较大范围的Inconel625高温合金的Johnson-Cook本构模型十分必要。

为了解决上述问题，本文作者在不同温度范围和应变率条件下对Inconel625高温合金进行准静态压缩试验和霍普金森压杆试验，分析其热变形规律，建立Inconel625高温合金的Johnson-Cook本构模型，分析其应力应变关系，计算模型的相关度和绝对误差，并在此基础上对模型做进一步修正，使其能够更加准确地反映Inconel625高温合金在较高温度和应变率变化范围内的热变形行为。

1  试验

1.1  试验材料及试样制备

本试验所用材料为锻态Inconel625高温合金棒材，其化学成分见表1。试验分两阶段：第一阶段为Inconel625高温合金的准静态压缩试验，第二阶段为Inconel625高温合金的霍普金森压杆试验。准静态压缩试验采用d 5 mm×5 mm的圆柱形试样，除几何尺寸要求外，还要有较好的平行度和垂直度，均保持在0.01 mm左右，表面粗糙度为1.6 mm。霍普金森压杆试验在两套压杆装置上进行，采用圆柱形试样，试样规格分别为d 5 mm×5mm、d 4 mm×4 mm、d 2 mm× 2 mm，试样的加工精度和加工方式与准静态压缩试验相同。

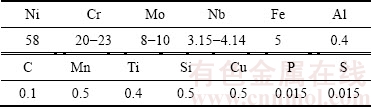
表1  Inconel625高温合金的化学成分

Table 1  Chemical composition of Inconel625 alloy (mass fraction, %)

1.2  试验方法

在CSS电子万能试验机上进行的准静态压缩试验，试验条件为室温(20 ℃)，选取应变速率为0.001 s^-1，压缩速率为0.3 mm/min。试验采用d 5 mm×5 mm试样，为减小试验误差，试验重复进行3次。

在霍普金森压杆试验装置上进行的动态力学性能试验，设计试验温度为20~800 ℃，应变率为1500~ 8000 s^-1。试验采用d 5 mm×5 mm，d 4 mm×4 mm和d 2 mm×2 mm 3种试样，其中d 5 mm×5 mm，d 4 mm×4 mm的试样用于低应变率条件下，用直径为13 mm的撞击杆、入射杆和透射杆进行试验；d 2 mm×2 mm的试样用于高应变率条件下，用直径为5 mm的撞击杆、入射杆和透射杆进行试验。为减小试验误差，每组试验重复进行3次。具体试验方案如表2所列。

表2  霍普金森压杆试验方案

Table 2  Project of split Hopkinson pressure bar experiment

2  结果及分析

2.1  准静态压缩试验

材料的真实应力-应变之间的关系能直接反映出材料流动应力与变形条件之间的关系，同时也是材料内部组织性能变化的宏观表现。从材料的真实应力-应变曲线上可以看出，材料在变形过程中是否发生动态再结晶，当真实应力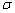随真实应变的增加而增加时，材料发生加工硬化。

Inconel625高温合金的准静态压缩试验真实应 力-应变曲线如图1所示，从图1中可以看出，材料的真实应力随应变的增加而增加，在准静态载荷压缩状态下材料没有明显的屈服阶段，也没有产生动态再结晶，但有明显的加工硬化产生，这是由于金属材料在形成塑性变形时，金属晶格发生了弹性畸变，这就阻碍了金属内部的滑移。畸变越严重，则塑性变形产生越困难、变形抗力越大。随着变形程度增加，晶格的畸变也随之增大导致滑移带产生较严重的弯曲，这使得金属变形抗力变得更大，出现加工硬化。

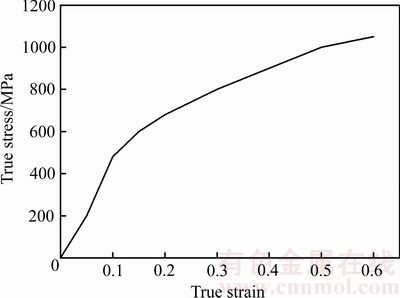
图1  准静态压缩真实应力-应变曲线

Fig. 1  Curve of true stress-strain obtained by quasi-static compression experiment

图2  Inconel625高温合金在同一温度不同应变率下的真实应力-应变曲线

Fig. 2  True stress-strain curves of Inconel625 alloy at same temperature and different strain rates

2.2  霍普金森压杆试验

图2所示为Inconel625高温合金在20，200，400，600，800 ℃时不同应变率下的真应力-应变曲线。图2(a)所示为常温下霍普金森压杆试验在不同应变率下的真实应力-应变曲线，由图2可知在弹性段，Inconel625高温合金的流动应力与屈服应力先随着应变率的增大而增大，当应变率达到3500 s^-1时流动应力与屈服应力随着应变率的增大反而出现下降现象，说明该材料产生了显著的应变率敏感效应，是一种应变率敏感材料。在进入到塑性段后，应力随着应变的增大而增大，并基本呈线性趋势。比较图2(a)~(e)可知，在相同温度不同应变率条件下，材料的应变硬化率(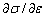)基本相同。随着动态压缩温度的升高，Inconel625高温合金的流动应力与屈服应力并不是单一的随应变率的增大而增大，这与现阶段流动应力随应变率增大而增大的趋势理论不完全吻合^[25-26]。在温度达到800 ℃时，材料的流动应力和屈服应力均随着应变率的增大而减小，这是由于在高速冲击载荷作用下，金属密度增大，并在材料内部形成缺陷，进而使材料表现出应变率强化效应和应变强化效应，但这两种效应并不是无限增长的，当其达到饱和状态时，高温会促使材料再结晶，将内部缺陷自行减小。

从图2中可以看出，不同应变率条件下Inconel625高温合金的真实应力-应变曲线进入稳态流变阶段的起始应变值会随着试验条件的变化而变化，但是大部分曲线在真实应变超过0.05后会进入稳态流变阶段。为研究高温合金IN625对温度的敏感性，本文作者选取各曲线在真应变为0.05~0.15范围内的一段作为构造本构方程的数据来源。

图3所示为材料在不同温度条件下应变率分别为1500、3500、6000、8000 s^-1时的真实应力-应变曲线。由图3可知，在相同应变率条件下材料的应变硬化率随温度的升高而降低，在高应变率下，Inconel625高温合金具有显著的温度敏感性，且材料的塑性流动应力和屈服应力随温度的升高而逐渐减小，存在明显的温度软化效应。综合分析可以得出，Inconel625高温合金是一种应变率敏感、温度敏感材料，在高温、高应变率条件下，材料的塑性变形过程存在应变硬化效应、应变率硬化效应及温度软化效应的耦合作用，从而决定了该材料真应力-应变曲线的变化趋势。

3  本构模型的建立

3.1  原始的Johnson-Cook本构模型

假设材料应力符合屈服准则和各项同性应变硬化准则，则屈服极限为^[28-30]

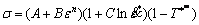             (1)

式中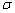：为材料的屈服极限；为材料的等效塑性应变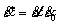；为无量纲的塑性应变率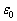；为参考应变率；n为应变硬化指数；C为应变率敏感系数；m为温度软化指数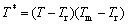；，其中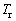是参考温度，为材料的熔点温度。

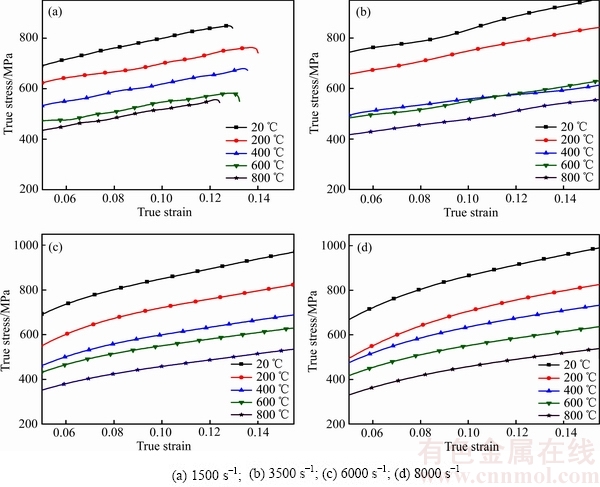
图3  Inconel625高温合金在同一应变率不同温度下的真实应力-应变曲线

Fig. 3  True stress-strain curves of Inconel625 alloy at same strain rate and different temperatures

原始Johnson-Cook本构模型的基本形式如式(1)所示，其中包含3个部分，共A、B、n、C、m 5个材料参数。在确定模型各参数时分别考虑各因素对流动 应力的影响，首先忽略应变率效应及温度软化效应，相当于式(1)等式右边的后两项为1，因此，式(1)可变为

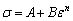                                (2)

式中：A为参考温度(T_r=20 ℃)、参考应变率(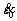=0.001 s^-1)条件下的初始屈服应力，可直接由图2中准静态压缩试验的真实应力-应变曲线中读取A=490 MPa，然后取强化段数据，将式(2)转化为式(3)的形式，此式可看做斜率为n，截距为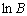的直线，将强化段数据进行拟合可得到：n=1.097，B=1283.4 MPa。

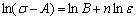                       (3)

为了得到应变率强化系数C，取室温高应变率下的数据，即取应变率为1500、3500、6000、8000 s^-1，应变为0.1时所对应的应力进行拟合。由于在室温下取值，所以此时温度项为1，式(2)可变为：

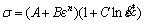                     (4)

将式(4)两边都除以，可得：

                       (5)

式(5)可看做是斜率为C，截距为1的直线，经数据拟合得出C=0.027。

为了进一步确定温度软化系数m，取相同应变率不同温度条件下的压缩数据，对不同温度下材料的应力值进行拟合。按照上述方法将式(2)转换成一条双对数坐标上的直线：

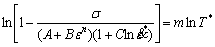          (6)

由于材料在产生塑性变形过程中会产生一定的热量，使材料发生温度软化效应，降低材料的流动应力，因此，材料在求解温度软化系数m时要考虑塑性变形所引起的材料温度的升高即绝热温升的影响。

材料在发生塑性变形时所做的功有很大一部分转化成了热量，如式(7)所示：

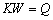                                   (7)

式中：W为材料在动态冲击下塑性变形所做的功；Q为变形时所转化的热量；k为转化系数；W和Q又可经过一系列变换，经过推导得出温度增量的表达式(8)，如下式所示：

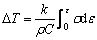                             (8)

式中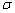：为真实应力；为真实应变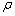；为材料密度；C为当前温度下材料的比热容，C值由经验值获得，根据KHAN等^[25]的研究成果，k取0.9，即塑性变形过程中所做的功有90%转化为热量。因此塑性变形过程中的材料的温度T必须在原始温度T₀的基础上考虑温度增量，即

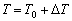                                (9)

Inconel625高温合金的熔点温度为1290~1350 ℃，计算时取材料的熔点温度T_m=1320 ℃，因此，考虑绝热温升的影响并将数据拟合可得到m=0.49。

通过以上分析及计算可得Inconel625高温合金的原始Johnson-Cook本构模型为

    (10)

Inconel625高温合金的原始Johnson-Cook本构模型参数见表3。

表3  Inconel625高温合金的原始Johnson-Cook本构模型参数

Table 3  Original Johnson-Cook model parameters of Inconel625 alloy

3.2  分析与改进

3.2.1  原始Johnson-Cook本构模型的拟合结果分析

根据表3作出图4，即流变应力预测值与试验值的比较。一般情况下，需要流变应力的预测值与试验值越接近越好，因此需要对预测结果与试验结果从符合程度上进行分析说明。相关系数(相关度)就是一个常用的统计数据的方法，它一般用来表示计算值与试验值的符合程度。其数学表达式为^[29]

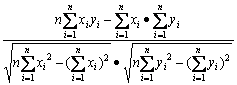          (11)

式中：n为观测点总数；x_i为试验测得的流动应力；y_i为模型的预测值；和分别为x_i和y_i平均值。但是，如果只用相关系数来表示计算结果的好坏，这是片面的。相关系数越高，可能数据的符合程度越好，但是并不是绝对的，因此，还需要引入绝对误差来表示计算结果和试验值的偏离程度。绝对误差可以表示为

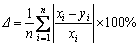                     (12)

图4中图例ED表示试验数据，PJC表示拟合数据。图4(a)~(d)分别表示了应变速率为1500、3500、6000、8000 s^-1下的真实应力-应变曲线的拟合值与试验值，能够明显看出，模型在20、200、400 ℃时拟合曲线与试验曲线差别不大，而在600和800 ℃下曲线拟合的误差较大。尽管拟合曲线与试验曲线较为吻合，但依然存在10%左右的平均误差。

图5所示为原始Johnson-Cook本构模型模拟应力与试验应力的离散程度，即相关情况。图5中黑色的直线代表相关度为1(100%)，落在上面的点代表了模拟值与试验值完全一致，直线上方的点模拟值大于试验值，直线下方的点模拟值小于试验值，不同颜色的点表示在不同应变率条件下的数据。Inconel625高温合金的流动应力的原始Johnson-Cook本构模型计算值与试验值的相关度仅为0.901。在图5中试验平均值曲线与拟合平均值曲线的符合程度对比，其绝对误差为10.13%。

由图4和5可知，原始Johnson-Cook本构模型不能够准确描述Inconel625高温合金在切削过程中的流变行为，原因在于原始Johnson-Cook本构模型是建立在诸多前提假设条件之下的。

原始Johnson-Cook本构模型认为应变硬化与应变硬化速率以及加热软化效应这3个因素是相互独立、互不干扰的，事实上对于Inconel625高温合金，应变硬化系数C是随着温度和应变的变化而变化的。为了更加准确地描述Inconel625高温合金的流变行为，必须考虑这三者之间的关系，以及这三者对流动应力的交互作用。

3.2.2  对原始Johnson-Cook本构模型的改进

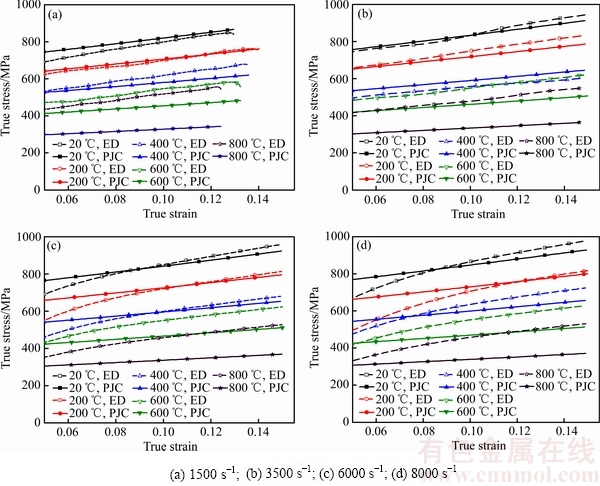
图4  Inconel625高温合金原始的Johnson-Cook本构模型计算值与试验值的比较

Fig. 4  Comparison of Inconel625 alloy of experimental value and the predicted value of original Johnson-Cook model

图5  原始Johnson-Cook本构模型预测值和试验值的相关度

Fig. 5  Correlation between experimental and predicted flow stress of original Johnson-Cook model

通过图1可知，Inconel625高温合金在大部分切削条件下的真应力-真应变曲线在进入稳态流变后呈现平稳延伸的特点。在试验中曲线却呈现出持续上升的趋势，这表明Inconel625高温合金在这些条件下变形时应变硬化作用强于动态再结晶的软化作用，流变应力随应变增大而不断增大。由图4和5可以看出，模拟值与试验值存在较大差距，这表明原始JC模型不能很好地表达出Inconel625高温合金在车削过程中的动态特性。针对上述问题，对原始Johnson-Cook本构模型进行了改进。观察式(1)可知，第1乘项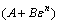对式子的拟合结果起主导作用，决定了应力的大概分布范围。后面2个乘项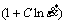和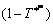分别在参考温度点和参考应变速率时为1，因此，当温度为参考温度、应变速率为参考应变速率时，这两项不影响计算结果，但这两项会在温度和应变速率偏离参考点时发挥对流动应力计算结果的调整作用。因温度和应变速率的改变而引起的应力变化即由这两项反映出来。应变速率硬化系数C和加热软化指数m决定了调整的幅度。在原始模型中，参数C是作为一个常数引进的，而实际上参数C并非是一个常数，是随着温度和应变速率而变化的。因此参数C必须修改为一个随温度和应变速率变化的量。选用幂函数修改参数C为

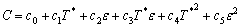      (13)

式中：c₀~c₅为待定的系数。

修改后的Johnson-Cook本构模型各参数的求解过程如下。首先令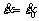。此时中间乘项，解出B、n、m 3个参数，再用全试验范围的数据解出c₀~c₅。改进后的Johnson-Cook本构模型参数拟合结果如表4和5所列。根据表4和5的参数，计算出流动应力值，并与实际结果做比较，其结果如图6所示。

表4  改进后的Johnson-Cook本构模型参数B、n、m的值

Table 4  Values of B, n, m of modified Johnson-Cook model

表5  改进后的Johnson-Cook本构模型参数C的系数

Table 5  Coefficients of parameter C of modified Johnson- Cook model

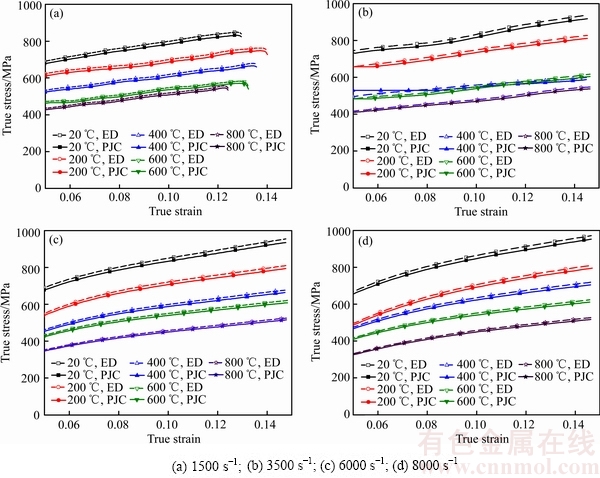
图6  Inconel625高温合金改进的Johnson-Cook本构模型计算值与试验值的比较

Fig. 6  Comparison of Inconel625 alloy of experimental value and predicted value of modified Johnson-Cook model

图7所示为改进后的模型预测值与试验值的相关度。从图7中能够看到绝大多数点都在直线的下方，这是由于选取的应变率硬化系数C的多项式函数对温度带来的影响计算偏小造成的。然而，经过改进后JC模型的相关系数和绝对误差都有显著改善，说明改进后的模型能够很好地表达出Inconel625高温合金在高速车削过程中的高温热变形行为。

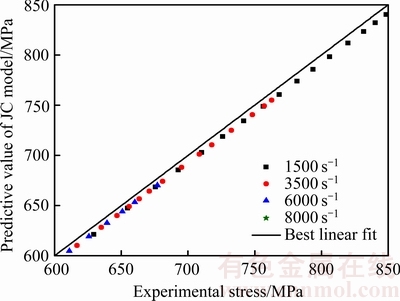
图7改进的Johnson-Cook本构模型预测值和试验值相关度

Fig.7 Correlation coefficient between modified Johnson-Cook model and experiment data over entire range

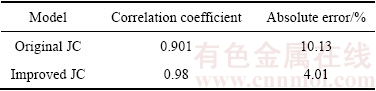
由表6可知，改进后模型的相关系数是0.98，比原始模型高；改进后模型的绝对误差为4.01%，比原始模型低。改进后的模型能够更好地表征Inconel625高温合金的高温热变形行为。

表6  两种本构模型的相关度和绝对误差

Table 6  Correlation coefficient and absolute error of two models

4  结论

1) 通过对Inconel625高温合金在温度为20~800 ℃，应变率为0.001~8000 s^-1的范围内进行试验，得到了材料在常温低应变率及高温高应变率下的真实应 力-应变关系。试验结果表明：随着温度的升高，Inconel625高温合金的流动应力与屈服应力并不单一随应变与应变率的增大而增大，同一温度、不同应变率条件下，随着应变率的增加，真实应力减小；同一应变率、不同温度条件下，随着温度而升高，真实应力减小。

2) 利用准静态压缩试验和霍普金森压杆试验得到的数据，建立Inconel625高温合金在较高应变率和温度范围的原始Johnson-Cook本构模型，并通过温度与应变率对参数C的影响规律对原始Johnson-Cook本构模型进行了改进，提高了模型的相关度(由0.901提高到0.98)，并降低了模型的绝对误差(由10.13%降低到4.01%)，进一步提高了模型对不同温度与不同应变速率的符合程度，更好地描述在较高温度和应变率变化范围的Inconel625高温合金的热变形行为。

REFERENCES

[1] CHOUDHURY I A, EL-BARADIE M A. Machinability assessment of inconel 718 by factorial design of experiment coupled with response surface methodology[J]. Journal of Materials Processing Technology, 1999, 95(1/3): 30-39.

[2] SETTINERI L, FAGA M G, LERGA B. Properties and performances of innovative coated tools for turning inconel[J]. International Journal of Machine Tools & Manufacture, 2008, 48(7/8): 815-823.

[3] THAKUR D G, RAMAMOORTHY B, VIJAYARAGHAVAN L. A study on the parameters in high-speed turning of superalloy Inconel 718[J]. Materials and Manufacturing Processes, 2009: 244.

[4] 张慧萍, 李振加, 刘二亮, 魏国梁. 高速切削切屑折断界限变化规律[J]. 机械工程学报, 2008, 44(5): 124-130.

ZHANG Hui-ping, LI Zhen-jia, LIU Er-liang, WEI Guo-liang. Change regulation of chip breaking limit in high speed cutting[J]. Journal of Mechanical Engineering, 2008, 44(5): 124-130.

[5] WU Kai, LIU Guo-quan, HU Ben-fu, LI Feng, ZHANG Yi-wen, TAO Yu, LIU Jian-tao. Hot compressive deformation behavior of a new hot isostatically pressed Ni-Cr-Co based powder metallurgy superalloy[J]. Materials & Design, 2011, 32(4): 1872-1879.

[6] DENG Jian-xin, LIU Li-li. Failure mechanisms of particle and SiC whisker reinforced Al₂O₃ ceramic tools when machining nickel-based alloys[J]. International Journal of Machine Tools and Manufacture, 2005, 45: 1393-1401.

[7] FEYZI T, SAFAVI S M. Improving machinability of Inconel 718 with a new hybrid machining technique[J]. The International Journal of Advanced Manufacturing Technology, 2013: 66(5/8): 1025-1030.

[8] 魏洪亮, 杨晓光, 于慧臣. GH4169合金高温力学行为本构建模及参数识别[J]. 材料工程, 2005(4): 42-45.

WEI Hong-liang, YANG Xiao-guang, YU Hui-chen. Constitutive modeling and parameter identification of mechanical behavior of GH4169 alloy at elevated temperature[J]. Material Engineering, 2005(4): 42-45.

[9] 李川平. Ti6Al4V钛合金动态本构模型与高速切削有限元模拟研究[D]. 兰州: 兰州理工大学, 2011.

LI Chuan-ping. Dynamic constitutive model of Ti6Al4V titanium alloy and finite element simulation of high speed cutting[D]. Lanzhou: Lanzhou University of Technology, 2011.

[10] 王敏杰, 谷丽瑶. 高速切削过程绝热剪切局部化断裂判据[J]. 机械工程学报, 2013, 49(1): 156-163.

WANG Min-jie, GU Li-yao. Fracture criterion of adiabatic shear localization in high speed machining[J]. Journal of Mechanical Engineering, 2013, 49(1): 156-163.

[11] 杨奇彪, 刘战强, 曹成铭, 杜 劲. 高温合金高速切削锯齿形切屑应变与应变率研究[J]. 农业机械学报, 2011, 42(2): 225-228.

YANG Qi-biao, LIU Zhan-qiang, CAO Cheng-ming, DU Jin. Study on saw chip strain and strain rate in high speed alloy cutting[J]. Journal of Agricultural Machinery, 2011, 42(2): 225-228.

[12] BARDI F, CABIBBO M, EVANGELISTA E. An analysis of hot deformation of an Al-Cu-Mg alloy produced by powder metallurgy[J]. Materials Science & Engineering A, 2003: 3391.

[13] 陈 刚, 陈忠富, 陶俊林, 牛 伟, 张青平, 黄西成. 45钢动态塑性本构参量与验证[J]. 爆炸与冲击, 2005(5): 69-74.

CHEN Gang, CHEN Zhong-fu, TAO Jun-lin, NIU Wei, ZHANG Qing-ping, HUANG Xi-cheng. Dynamic plastic constitutive parameters and verification of 45 steel[J]. Explosion and Shock, 2005(5): 69-74.

[14] LIU G, CHEN M, SHEN Z. Experimental studies on machinability of six kinds of nickel-based superalloys[J]. J Machining and Machinability of Materials, 2006(3): 287-300.

[15] 曹自洋, 何 宁, 李 亮, 朱文明. 高速切削钛合金Ti6Al4V切屑的形成及其数值模拟[J]. 中国机械工程, 2008, 20: 2450-2454.

CAO Zi-yang, HE Ning, LI Liang, ZHU Wen-ming. Formation and numerical simulation of Ti6Al4V chip in high speed cutting titanium alloy[J]. China Mechanical Engineering, 2008, 20: 2450-2454.

[16] HOU Q Y, WANG J T. A modified Johnson-Cook constitutive model for Mg-Gd-Y alloy extended to a wide range of temperatures[J]. Computational Materials Science, 2010, 50(1): 147-152.

[17] 李淼泉, 姚晓燕, 罗 皎, 林莺莺, 苏少博, 王海荣. 镍基高温合金GH4169高温变形流动应力模型研究[J]. 金属学报, 2007(9): 937-942.

LI Miao-quan, YAO Xiao-yan, LUO Jiao, LIN Ying-ying, SU Shao-bo, WANG Hai-rong. Study on high temperature deformation flow stress model of nickel base superalloy GH4169[J]. Journal of Metals, 2007(9): 937-942.

[18] 宋迎东, 高德平, 杨治国. 粉末高温合金粘塑性试验评定与本构模型参数估计[J]. 航空学报, 2002(2): 162-165.

SONG Ying-dong, GAO De-ping, YANG Zhi-guo. Evaluation of viscoplastic test and parameter estimation of constitutive model for powder superalloy[J]. Journal of Aeronautics, 2002(2): 162-165.

[19] 闫士彩, 程 明, 张士宏, 张海燕, 张伟红, 张立文. Inconel625合金的高温高速热变形行为[J]. 材料研究学报, 2010, 24(3): 239-244.

YAN Shi-cai, CHENG Ming, ZHANG Shi-hong, ZHANG Hai-yan, ZHANG Wei-hong, ZHANG Li-wen. High temperature and high speed thermal deformation behavior of Inconel625 alloy[J]. Journal of Materials Research, 2010, 24(3): 239-244.

[20] 丰建朋, 张麦仓, 罗子健, 郭 灵, 张 华. 应用神经网络表征变形高温合金的本构关系[J]. 锻压技术, 1998(1): 31-35.

FENG Jian-peng, ZHANG Mai-cang, LUO Zi-jian, GUO Ling, ZHANG Hua. Characterization of deformation superalloys by neural networks[J]. Forging and Stamping Technology, 1998(1): 31-35.

[21] 段春争, 王肇喜, 李红华. 高速切削锯齿形切屑形成过程的有限元模拟[J]. 哈尔滨工程大学学报, 2014(2): 226-232.

DUAN Chun-zheng, WANG Zhao-xi, LI Hong-hua. Finite element simulation of serrated chip formation during high speed cutting[J]. Journal of Harbin Engineering University, 2014(2): 226-232.

[22] 严宏志, 龚黎军. 20CrMo材料本构模型及其有限元模拟[J]. 中南大学学报(自然科学版), 2012, 43(11): 4268-4273.

YAN Hong-zhi, GONG Li-jun. 20CrMo material constitutive model and its finite element simulation[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4268-4273.

[23] 俞秋景, 刘军和, 张伟红, 于连旭, 刘 芳, 孙文儒, 胡壮麟. Inconel 625合金Johnson-Cook本构模型的一种改进[J]. 稀有金属材料与工程, 2013(8): 3-6.

YU Qiu-jing, LIU Jun-he, ZHANG Wei-hong, YU Lian-xu, LIU Fang, SUN Wen-ru, HU Zhuang-lin. An improvement of Johnson-Cook constitutive model for Inconel 625 alloy[J]. Rare Metal Materials and Engineering, 2013(8): 3-6.

[24] 黄西成, 胡文军. Johnson-Cook本构参数的确定方法[C]// 中国力学学会爆炸力学实验技术专业组. 第六届全国爆炸力学实验技术学术会议论文集. 安徽: 中国力学学会爆炸力学实验技术专业组, 2010: 308-315.

HUANG Xi-cheng, HU Wen-jun. Determination method of constitutive parameters of Johnson-Cook[C]// Proceedings of the Sixth National Symposium on Explosive Mechanics Experiment of China Mechanics Association. Anhui Province: Chinese Academy of Mechanics Explosion Mechanics Experiment Technology Specialty Group, 2010: 308-315.

[25] KHAN A S, SUH Y S, KAZMI R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys[J]. International Journal of Plasticity, 2004, 20(12): 2233-2248.

[26] 鲁世红. 高速切削锯齿形切屑的实验研究与本构建模[D]. 南京: 南京航空航天大学, 2009.

LU Shi-hong. Experimental study and constitutive modeling of serrated chip for high speed cutting[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[27] 鲁世红, 何 宁. H13淬硬钢高应变速率动态性能的实验与本构模型研究[J]. 中国机械工程, 2008, 19: 2382-2385.

LU Shi-hong, HE Ning. The transmission rate of the dynamic performance experiment and study on constitutive model[J]. China Mechanical Engineering, 2008, 19: 2382-2385.

[28] HOLCKA M, LEEMET T, SHROT A. Characterization and numerical modeling of high strain rate mechanical behavior of Ti-15-3 alloy for machining simulations[J]. Materials Science and Engineering A, 2012, 550: 350-357.

[29] 常列珍, 潘玉田, 张治民, 薛 勇. 一种调质50SiMnVB钢Johnson-Cook本构模型的建立[J]. 兵器材料科学与工程, 2010(4): 68-72.

CHANG Lie-zhen, PAN Yu-tian, ZHANG Zhi-min, XUE Yong. Establishment of a Johnson-Cook constitutive model for quenched and tempered 50SiMnVB steel[J]. Ordnance Material Science and Engineering, 2010(4): 68-72.

[30] RULE W K, JONES S E. A revised form for the Johnson-Cook strength model[J]. International Journal of Impact Engineering, 1998, 21(8): 609-624.

J-C constitutive modeling of high temperature alloys Inconel625

LIU Er-liang, XING Hong-wei, WANG Ming-ming, XU Zhi-chao, ZHAO Na

(School of Mechanical Engineering, Harbin University of Science and Technology, Harbin 150080, China)

Abstract: In order to study the thermal deformation behavior of Inconel625 superalloy at high temperature and strain rate range, the quasi-static test and Hopkinson pressure bar test of Inconel625 superalloy were carried out by using CSS electronic universal testing machine and split type pressure bar test device. The true stress-strain curves of Inconel625 superalloy were obtained in the range of 20-800 ℃ centigrade and strain rate of 0.001-8000 s^-1. The experimental results show that the low stress and yield stress of Inconel625 superalloy do not increase with the increase of strain rate. Under the same temperature, the true stress of Inconel625 superalloy increases first and then decreases with the increase of strain rate (the dividing line is strain rate of 6000 s^-1). While under the same strain rate, the true stress of Inconel625 superalloy decreases with the increase of temperature. Based on the Johnson-Cook model, the true stress-strain curves are fitted and analyzed. The correlation coefficient and the absolute error between the predicted value and the experimental value are obtained by calculation. By improving the Johnson-Cook constitutive model of Inconel625 superalloy, the model can be used to characterize the themal deformation of Inconel625 superalloy at high temperature and strain rate range.

Key words: Inconel625 superalloy; Johnson-Cook constitutive model; strain; thermal deformation

Foundation item: Project (51475126) supported by the National Natural Science Foundation of China

Received date: 2017-01-18; Accepted date: 2017-07-26

Corresponding author: LIU Er-liang; Tel: +86-13946050530；E-mail: elliu@163.com

(编辑  王  超)

基金项目：国家自然科学基金资助项目(51475126)

收稿日期：2017-01-18；修订日期：2017-07-26

通信作者： 刘二亮，副教授，博士；电话：13946050530；E-mail: elliu@163.com