DOI：10.19476/j.ysxb.1004.0609.2018.10.24

充填体孔隙结构与中观参数跨尺度关联特征

胡建华，蒋  权，任启帆，丁啸天

(中南大学 资源与安全工程学院，长沙 410083)

摘  要：充填体的孔隙结构特征对充填材料的力学性质直接产生影响，是充填体多尺度力学研究的基础。以体视学、分形理论为基础，利用充填体孔隙结构SEM图像，通过最大类间方差法、盒维数法计算其微观孔隙结构分形维数，获得充填材料孔隙结构定量表征，分析充填体分形维数与单轴抗压强度、含水率、孔隙度等中观参数的相关性，探究SEM像定量分析与充填体中观参数的跨尺度关联关系。结果表明：石粉水泥全尾胶结充填体微观孔隙结构分形维数可以表征孔隙结构的复杂程度；孔隙结构的分形维数与充填体的中观参数间具有一定的关系，其中与单轴抗压强度存在负相关性，与含水率存在正相关性；建立孔隙结构特征分形维数与单轴抗压强度、含水率的关联曲线，获得关联特征值的均方差，分形维数与单轴抗压强度和含水率的均方差值分别为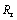=-0.638和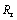=0.604。

关键词：充填体；分形维数；孔隙结构；相关性

文章编号：1004-0609(2018)-10-2154-10　　     中图分类号：TD853.34　　     文献标志码：A

尾砂胶结充填采矿中，确定合理的充填体强度成为安全开采的关键，影响充填体强度的细观孔隙结构和分布规律又是充填体强度的控制因素之一。对于尾砂胶结充填体孔隙结构的研究，多集中于SEM微观结构图以及NMR核磁孔隙度测试。国际上，KOOHESTANI等^[1]通过SEM图像对木浆掺料充填体孔隙进行结构及成分上的定性分析；FRIDJONSSON等^[2]以NMR以及压汞实验为基础对充填体孔结构、细观成分进行分析进而对中观单轴抗压强度、渗透率等参数进行解释。国内研究者艾凯明^[3]尝试利用NMR对孔隙变化进行分析，侯永强等^[4]通过NMR实验建立核磁孔隙度与料浆浓度的关系，李鑫等^[5]利用SEM对Aft等充填体水化反应生成物进行了辨识分析。一般而言，对于SEM像的研究分析多以定性分析为主，研究内容为孔径粗略测量、水化产物辨识、成分与结构分析等。张雄等^[6]在对混凝土微观结构进行分析时引入了体视学原理^[7]作为材料截面图定量分析的理论基础，以及将研究对象截面与整体建立相关性的理论基础。由体视学原理，认为通过材料的二维截面可以确定其三维结果，这一理论被广泛应用到材料截面的研究当中，用以证明通过分析SEM、CT像等所得的数据与整个研究对象属性的一致性，由此对于材料二维图像的研究得以加入定量的分析^[8]。在此基础上，将MANDELBROT^[9]提出的分形理论作为研究方法引入，丰富了对于研究对象结构分析的方法。近两年的实验中，田威等^[10]在CT扫描混凝土冻融损伤的实验中引入了分形维数计算；王月香等^[11]计算了天然硅藻土SEM像的分形维数；陆春华等^[12]以分形维数作为锈蚀钢筋表面轮廓的表征依方法；分形维数也应用于人体骨骼结构、天然材料结构的研究^[13-14]。利用分形维数来分析材料的孔隙结构时，一般认为无序性更高的孔隙结构表现出更高的分形维数，充填体孔隙结构的定量分析以此作为理论以及应用的基础。分形维数也可与其他实验参数建立相关性，孙建平等^[15]借由海相页岩SEM像分形维数的分析，建立了分形维数与甲烷吸附力的关系；研究人员在岩土力学等研究中也引入了分形维数，用以进行结构分形维数与其他各项参数的相关性分析^[16-19]。上述实验中，研究对象的分形维数数据基础多由压汞实验、CT扫描及SEM像等获取。对于SEM像，通过一系列的图像识别、处理、计算等操作，其分形维数计算得以实现^[20-22]。实验研究结果表明，岩体、水泥胶结材料等的孔隙结构，在微观尺度上表现出明显的分形特征^[23-24]。

分型理论提升了SEM像数据的挖掘程度，基于该理论对SEM微观孔隙结构图进行定量分析，可以促进SEM与NMR实验结果的研究相关性。然而，目前充填体孔隙结构SEM像的分析多停留于定性层面，对于充填体细观结构与中观参数间的多尺度参数的相关性缺乏研究。本文作者以体视学、分形等理论为基础，以石粉水泥全尾胶结充填体为研究对象，利用最大类间方差法、盒维数法等计算方法，对微观孔隙结构SEM像进行图像处理以及分形维数计算，建立孔隙结构的分形维数与单轴抗压强度、孔隙度和含水率等相关参数的定量分析，探讨研究充填体微观孔隙结构分形维数与各实验数据的相关性，提供一种跨尺度定量研究的新途径。

1  实验

1.1  实验材料

实验以某锡矿老式选矿工艺尾砂A组与新式选矿工艺尾砂B组作为充填骨料，将矿山废弃硅质灰岩通过容积35 L，筒体转速150 r/min的卧式球磨机，加工时间20 min，制成一定粒径范围的石粉用以替代部分水泥，选取长沙新星水泥厂出产强度等级为C30的P·042.5级水泥作为胶结材料。利用荷兰 PANalytical XRF spectrometers对实验原材料主要元素占比进行分析，结果如表1所列。

表1  原材料主要元素含量

Table 1  Primary element ratio

利用英国马尔文仪器有限公司Mastersizer2000，对实验原材料进行激光粒度分析实验，结果如图1所示。

图1  原材料粒度分布

Fig. 1  Particle size distribution of raw materials

1.2  料浆配比设计与研究

实验设计水灰比2.14，灰砂比1:4，控制变量为石粉替代水泥量，设置全水泥A1、B1组作为对照组，每组设置3块试样作为对照以减小误差，试模尺寸为(70.7 mm×70.7 mm×70.7 mm)。依照相同配比设计(15 mm×15 mm×15 mm)试模制作核磁共振实验试块。将尾砂与石粉视作骨料部分，引入不均匀系数C_u=d₆₀/d₁₀与曲率系数C_c=(d₃₀×d₃₀)/(d₆₀×d₁₀)，认为C_u＞10且1＜C_c＜3的骨料为级配良好，同时注意C_u过大则存在粒径缺失。其中d_p为累计占比达到目标比例的粒径值，由内插法公式可得粒径比计算如式(1)所示：

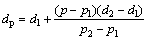                     (1)

式中：d_p为待求粒径；p为目标比例；p₁、p₂为p的相邻已知比例；d₁，d₂为相邻已知比例所对应的粒径。

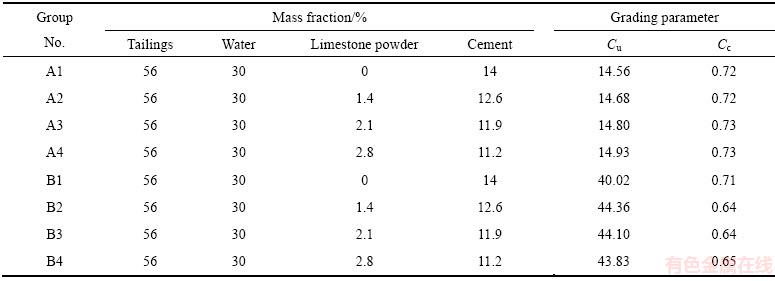
计算各组配比的不均匀系数C_u与曲率系数C_c，料浆中各成分占比及对应的评价参数如表2所列。

1.3  研究方法

以两种工艺尾砂及当地矿山废弃灰岩石粉为骨料，通过设计不同配比与养护时间得到16组石粉水泥全尾胶结充填体试块，开展试验探究充填体孔隙结构分形维数与中观参数相关性。通过单轴压缩仪进行单轴抗压强度实验；通过Ani-MR150岩石磁共振成像分析系统进行核磁共振含水率、孔隙度测试；通过捷克TESCAN MIRA3场发射扫描电镜进行SEM孔结构图像特征分析。通过MATLAB数学软件FRACLAB工具箱对SEM像进行灰度图转化、阈值计算、二值化、分形维数计算，得到各组试样微观孔隙分形维数数据，与强度、含水率、孔隙度等中观参数进行相关性分析，探究各项参数关联度水平。

表2  料浆配比

Table 2  Slurry ratio

2  结果与分析

2.1  强度与孔隙度实验

孔隙学理论拓展了孔隙研究的内容，该理论认为：相比于孔隙率，孔的结构对混凝土中观行为的影响更重要^[25-27]。在相同孔体积量的情况下，孔隙以不同形态、数量进行分布，其分形维数则不同。实验将孔隙结构分形维数作为描述孔隙分布特征的定量表达，充填体微观孔隙结构的分形维数因此可以客观反映其孔隙结构的优劣。对于水泥胶结充填体，其骨料级配、骨料成分、养护时间、生成物结构等因素都会对其分形维数产生影响。通过单轴抗压强度和核磁共振实验获取相关数据如表3所列，其中强度数据选取7 d、28 d强度，核磁共振实验由于7 d龄期试块无法进行保水，对7 d龄期试块运用核磁共振测试其含水率，对28 d龄期试块运用核磁共振测试孔隙度。

2.2  SEM像预处理

2.2.1  SEM像转灰度图

利用MATLAB软件，通过编程对各龄期与配比的充填体试块SEM像进行灰度图转化，计算适当的二值化灰度分割阈值，并进一步进行二值化处理。SEM原图去除底部参数栏后共1024×760=778240个像素点，其色彩接近于灰度图，通过MATLAB函数识别，SEM原图仍为彩色图像，需进行灰度换算将其转化为灰度图，从而进行灰度阈值计算。灰度值(g)共分为256阶(0~255)，对SEM原图使用浮点算法，通过公式g=R×0.3+G×0.59+B×0.11，R为红色值，G为绿色值，B为蓝色值，对图像单个像素点色光三原色逐一进行灰度换算，可得出对应像素点的灰度，利用MATLAB中的rgb2gray函数进行SEM图像-灰度图转化，结果如图2所示。

表3  中观实验数据

Table 3  Meso experimental data

2.2.2  灰度图二值化

图2  SEM转灰度图

Fig. 2  SEM conversion grayscale

图3  最大类间方差法灰度阈值计算流程图

Fig. 3  Flow chart for calculating gray threshold of maximum inter class variance method

最大类间方差法是一种自适应的图像分割阈值确定方法，其流程如图3所示，它按图像的灰度特性，将图像分成背景和目标2部分(对于充填体SEM孔隙结构图像，将灰度高的孔隙结构定义为背景，灰度低的反应产物与骨料定义为目标)，通过遍历灰度图的像素点并进行背景或目标的判定，计算两者与全图平均灰度的方差。以方差的增大为判定标准，当方差最大时的分割为最优解。这一算法可以使得错分概率最  小^[28]。在MATLAB中可以通过函数来调用最大类间方差法，进行图像分割阈值计算。通过调用graythresh函数，将256阶灰度等比例分为[0~1]之间的数值，对SEM灰度图进行分割阈值计算，计算结果如表4所列。

表4  灰度阈值计算结果

Table 4  Results of gray threshold calculation

以灰度分割阈值为基础，对灰度图的单个像素逐一进行二值化，由二值化判断函数：

                       (2)

式中：T为分割阈值，通过MATLAB中2bw二值化函数，将灰度低于或等于分割阈值T的像素点定值为0，即为黑点，将灰度高于T的像素点定值为1，即为白点，得到SEM二值化图像，与灰度图的对比如图4所示。

图4  灰度图—二值化图像对比

Fig. 4  Gray scale–binarized image contrast

2.3  SEM像分形维数计算

对于实际问题，若研究对象无明显的自相似性，通常使用盒维数法对其进行分形维数计算，利用MATLAB中针对分形维数计算的FRACLAB工具箱进行充填体试块SEM像的盒维数测试(SEM图像复杂度较高，需借助软件工具进行计算，以A1-7 d试块SEM像局部取样放大图进行具象化原理说明)，A1-7 d试块SEM局部图像盒维数计算过程如图5所示。

通过设置纵横比以及等分次数X，该工具箱将图片进行[0~X]次等分，在每次等分后，判定单位等分面积内是否存在背景区域(即有0值像素点存在)，将存在背景区域的单位等分面积记为一个“盒”，通过多次分割与计数(见图5(a))，最终得到由等分次数与盒数量构成的2^X-2^Y双指数坐标图(见图5(b))，其拟合直线斜率即为所求分形维数^{[11, 29]}。

部分试块SEM像盒维数测试结果如图6所示，其中X为等分次数，2^-X为单位盒相对于SEM图像的相对边长，2^Y为盒数量。需注意当等分次数X超过一定的值后，将得到趋于相同的盒数量，这是由于图像分辨率的限制。对于本实验的SEM像，盒数量上限为2^19.57，即当选取X＞10后，N数量将趋于不变，因此限制 X=[0~10]，在这一等分尺度内，测试结果展现出明显的分形特征。通过最小二乘法对测试点进行直线拟合，所得到的直线斜率即为该SEM像的盒维数。

通过获取拟合直线的斜率，得到相对应试样SEM微观孔隙结构图的盒维数以及28 d盒维数相对于7 d盒维数的变化情况，如图7所示。

3  分析与讨论

3.1 分形维数特性分析

A-7 d、B-7 d、A-28 d、B-28 d平均分形维数分别为1.789、1.790、1.802、1.803(见图7(a))，经过更长时间养护后，不同尾砂成分的充填体孔隙结构分形维数均有所提升。同时由图7(b)可知，相同尾砂不同配比下，充填体孔隙结构分形维数也以提升为主，表明随着水化反应进行，充填体孔隙结构的无序性提升，结构复杂度更高。原因主要是因为水化反应的C—H—S凝胶结构复杂，随着水化反应进行，C—H—S占比升高，从而孔隙结构的无序性提高导致的分形维数提升。

28 d养护龄期下两组充填体孔隙结构分形维数(见图7(a))较7 d实验结果表现出更高的一致性，其中在28 d试样中，水泥全尾对照组的差别最大，加入石粉后一致性提升，表明随着水化反应的进行，孔隙结构分形维数趋于稳定，且可以通过改变充填配比来影响孔隙结构分形维数。

同龄期下B组维数仅高出A组0.06%(见图7(a))，表明A、B组孔隙结构复杂程度相当，分析两者级配(见表2)，B组骨料不均匀系数C_u远大于10，表明中间粒径存在严重缺失，且曲率系数C_c劣于A组的，从而理论上B组充填体孔隙度将大于A组的，且孔隙分布将也将劣于A组的，表2孔隙度实验数据也与分析一致。

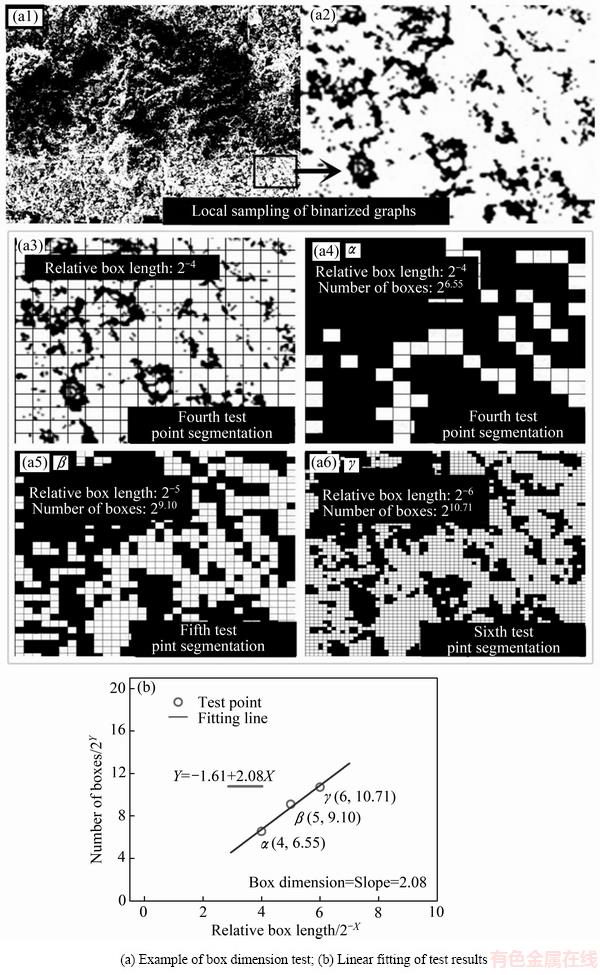
图5  盒维数计算过程

Fig. 5  Box dimension calculation

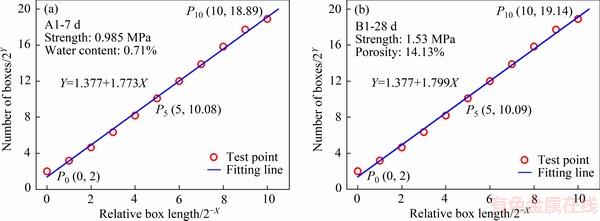
图6  盒维数测试与直线拟合

Fig. 6  Box dimension test and straight line fitting

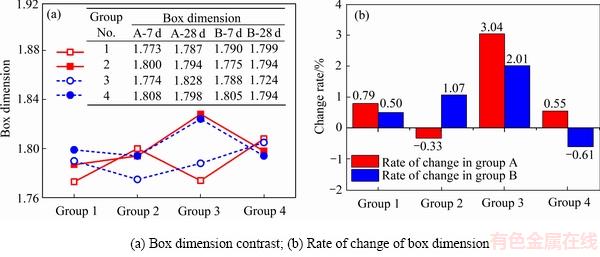
图7  盒维数分析

Fig. 7  Box dimension analysis

进一步分析可知，随着C—H—S凝胶结构的出现，一定程度上导致了不均匀性和曲率系数的影响减少。实验中级配与孔隙度对孔隙结构的影响不明确，因此不能由材料骨料的级配及孔隙度情况推断出孔隙结构的情况。在进行孔隙相关参数分析时，应当将孔隙结构与孔隙度、孔隙分布、级配等参数分开进行讨论^[30]。

3.2  中观实验参数相关性分析

将单轴抗压强度、含水率、孔隙度及分形维数等已知实验数据进行皮尔森积矩相关系数分析，均方差计算结果及直线拟合结果如图8所示。

孔隙结构分形维数与充填体强度表现出强相关性，其方差绝对值||均超过0.6。28 d养护龄期分形维数—强度皮尔森相关系数高于7 d养护龄期，表明维数与强度的相关性随着养护时间的提升有所增强。

7 d养护龄期下维数-强度-含水率相关性(见图8(a)，(b)，(c))：维数-强度、维数-含水率均表现出强相关性，前者为负相关，表明强度的升高会使得分形维数下降，充填体的强度受孔隙结构复杂程度的影响。维数-含水率的正相关表明分形维数的升高会使得含水率提升，孔隙结构复杂度的变化使得孔体表面积产生变化，从而影响了孔隙储水能力。强度-含水率的相关性不明确。

28 d养护龄期下维数-强度-孔隙度相关性(见图8(d)，(e)，(f))：维数-强度相关性保持稳定的强相关性，孔隙度与维数、强度的相关性不稳定，对于孔隙度(见表3)较低的A组，孔隙度与其他两者关系为极强相关性；对于孔隙度较高的B组，其维数-孔隙度、强度-孔隙度相关性不明确，原因在于B组骨料级配(见图1和表2)中间粒径缺失、存在一定量大颗粒尾 砂、不均匀系数过大，对充填体参数产生不利影响，且起主导作用。对于高孔隙度、高级配的尾砂胶结充填体，其参数相关性规律需在后续实验中进行深入研究。

图8  参数跨尺度相关性计算

Fig. 8  Cross scale correlation calculation of parameters

4  结论

1) 通过盒维数的分析方法，获得了石粉水泥全尾充填体孔隙结构SEM图像的分形维数，其数值介于1.773~1.828之间，均值为1.796，其分形维数值表明了石粉水泥全尾充填体具有相对稳定孔隙结构特征，有利于保持充填体的稳定性能。

2) 充填体的分形维数主要表征孔隙结构的复杂程度，在时间跨度上，7 d和28 d的分形维数差异性表现为孔隙结构分形维数随养护时间延长而升高，主要原因在于胶凝材料水化反应的影响，生成的C—   H—S凝胶结构使得充填体微观结构的复杂度提升。

3) 建立了充填体SEM微观孔隙结构分形维数与中观参数单轴抗压强度、孔隙度等的跨尺度关系函数，一定条件下分形维数与充填体强度存在负相关性，其均方差为=-0.638；与孔隙含水率存在正相关性，其均方差分别为=0.604。

REFERENCES

[1] KOOHESTANI B, KOUBAA A, BELEM T, BUSSIERE B, BOUZAHZAH H. Experimental investigation of mechanical and microstructural properties of cemented paste backfill containing maple-wood filler[J]. Construction and Building Materials, 2016, 121: 222-228.

[2] FRIDJONSSON E O, HASAN A, FOURIE A B, JOHNS M L. Pore structure in a gold mine cemented paste backfill[J]. MINERALS ENGINEERING, 2013, 53: 144-151.

[3] 艾凯明. 基于核磁共振的矿山充填料浆水分和孔隙演变研究[D]. 长沙: 中南大学, 2014.

AI Kai-ming. NMR studies of water and pore evolution in mine backfill slurry[D]. Changsha: Central South University, 2014.

[4] 侯永强, 王 磊, 张耀平, 邹雄刚. 孔隙度变化对充填体动载冲击变形的影响[J]. 化工矿物与加工, 2017(8): 60-62.

HOU Yong-qiang,WANG Lei, ZHANG Yao-ping, ZOU Xiong-gang. Influence of porosity variation on dynamic load impact deformation of backfill[J]. Industrial Minerals and Processing, 2017(8): 60-62.

[5] 李 鑫, 王炳文, 游家梁, 侯 阳, 解立赫, 李腾龙. 尾砂胶结充填体力学性能与微观结构研究[J]. 中国矿业, 2016, 25(6): 169-172.

LI Xin,WANG Bing-wen,YOU Jia-liang,YANG Han-wen, HOU Yang,XIE Li-he, LI Teng-long. Study on mechanical properties and microstructure of the cemented tailings backfill[J]. China Mining Magazine, 2016, 25(6): 169-172.

[6] 张 雄, 黄廷皓, 张永娟, 高 辉, 姜 曼. Image-Pro Plus混凝土孔结构图像分析方法[J]. 建筑材料学报, 2015(1): 177-182.

ZHANG Xiong,HUANG Ting-hao,ZHANG Yong-juan,GAO Hui,JIANG Man. Image-pro plus analysis of pore structure of concrete[J]. Journal of Building Materials, 2015(1): 177-182.

[7] SANDAU K. Three-dimensional measurement in microscopy[M]. Garland Science/BIOS Scientific Publishers, 1999: 89-90.

[8] 刘国权, 刘胜新, 黄启今, 钟云龙, 钟 声, 秦湘阁. 金相学和材料显微组织定量分析技术[J]. 中国体视学与图像分析, 2002(4): 248-251.

LIU Guo-quan, LIU Sheng-xin, HUANG Qi-jin, ZHONG Yun-long, ZHONG Sheng, QIN Xiang-ge. Metallography and quantitative analysis techniques of materials microstructure[J]. Chinese Journal of Stereology and Image Analysis, 2002(4): 248-251.

[9] MANDELBROT B. How long is the coast of britain? Statistical self-similarity and fractional dimension[J]. Science, 1967, 156(3775): 636.

[10] 田 威, 韩 女, 张鹏坤. 基于CT技术的混凝土孔隙结构冻融损伤试验[J]. 中南大学学报(自然科学版), 2017(11): 3069-3075.

TIAN Wei, HAN Nü, ZHANG Peng-kun. Experiments on the freeze-thaw damage of concrete porous structure based on CT technique[J]. Journal of Central South University(Science and Technology), 2017(11): 3069-3075.

[11] 王月香, 吉 锋, 顾欢达, 丁建文. 基于SEM图像处理的天然硅藻土分形特征分析[J]. 水利水运工程学报, 2017(5): 96-102.

WANG Yue-xiang, JI Feng, GU Huan-da, DING Jian-wen. Fractal characteristics of natural sedimentary diatomaceous earth based on SEM images[J]. Hydro-Science and Engineering, 2017(5): 96-102.

[12] 陆春华, 杨金木, 延永东, 傅巧瑛. 基于分形理论的锈蚀钢筋表面轮廓分布特征[J]. 江苏大学学报(自然科学版), 2018(1): 102-107.

LU Chun-hua, YANG Jin-mu, YAN Yong-dong, FU Qiao-ying. Surface profile distribution characteristics of corroded steel bar based on fractal theory[J]. Journal of Jiangsu University(Natural Science Edition), 2018(1): 102-107.

[13] LI A, DING W L, HE J, DAI P, YIN S, XIE F. Investigation of the pore structures and fractal characteristics of marine shale reservoirs using NMR experiments and image analyses: A case study of the Lower Cambrian Niutitang Formation in northern Guizhou Province, South China[J]. Marine and Petroleum Geology, 2018, 89(3): 530-540.

[14] MANGANO F, RASPANTI M, MAGHAIREH H, MANGANO C. Scanning electron microscope (SEM) evaluation of the interface between a nanostructured calcium-incorporated dental implant surface and the human bone[J]. Materials, 2017, 10(12): 1438.

[15] 孙建平, 胡英成, 王逢瑚, 韩天香. 基于图像处理的木材断裂面分形分析[J]. 仪器仪表学报, 2013(12): 2818-2823.

SUN Jian-ping, HU Ying-cheng, WANG Feng-hu, HAN Tian-xiang. Fractional analysis of wood fracture surface based on image processing[J]. Chinese Journal of Scientific Instrument, 2013(12): 2818-2823.

[16] ZHOU B, WANG J, WANG H. Three-dimensional sphericity, roundness and fractal dimension of sand particles[J]. GEOTECHNIQUE, 2018, 68(1): 18-30.

[17] 王 欣, 齐 梅, 李武广, 胡永乐, 刘 佳, 赵 凯. 基于分形理论的页岩储层微观孔隙结构评价[J]. 天然气地球科学, 2015(4): 754-759.

WANG Xin, QI Mei, LI Wu-guang, HU Yong-le, LIU Jia, ZHAO Kai. Micro-structure evaluation of shale gas reservoir based on fractal theory[J]. Natural Gas Geoscience, 2015(4): 754-759.

[18] 连会青, 冉 伟, 夏向学. 砂岩微观孔隙分形特征与宏观渗透性能的相关性[J]. 辽宁工程技术大学学报(自然科学版), 2017(6): 624-629.

LIAN Hui-qing,RAN Wei,XIA Xiang-xue. Theoretical research on correlation between microscopic fractal characteristics and macroscopic permmeability of sandstone[J]. Journal of Liaoning Technical University (Natural Science), 2017(6): 624-629.

[19] 刘传孝, 王 龙, 张晓雷, 李茂桐, 周 桐. 石灰岩断口细观复杂程度的分形几何学分析[J]. 重庆交通大学学报(自然科学版), 2017(7): 77-82.

LIU Chuan-xiao, WANG Long, ZHANG Xiao-lei, LI Mao-tong, ZHOU Tong. Fractal geometry analysis on complexity of limestone fracture mesoscale[J]. Journal of Chongqing Jiaotong University(Natural Science), 2017(7): 77-82.

[20] KIM J, CHOI Y C, CHOI S. Fractal characteristics of pore structures in GGBFS-based cement pastes[J]. Applied Surface Science, 2018, 428: 304-314.

[21] MORUZZI R B, de OLIVEIRA A L, DA C F, GREGORY J, CAMPOS L C. Fractal dimension of large aggregates under different flocculation conditions[J]. Science of the Total Environment, 2017, 609: 807-814.

[22] BUSHELL G C, YAN Y D, WOODFIELD D, RAPER J, AMAL R. On techniques for the measurement of the mass fractal dimension of aggregates[J]. Advances in Colloid and Interface Science, 2002, 95(1): 1-50.

[23] ZHU Qing-yong, YANG Wei-bin, YU Huai-zhong. Study on the permeability of red sandstone via image enhancement[J]. Fractals-Complex Geometry Patterns and Scaling in Nature and Society, 2017, 25(6): 1750055.

[24] 刘顺喜, 吴财芳. 比德-三塘盆地煤储层不同尺度孔隙分形特征研究[J]. 煤炭科学技术, 2016(2): 33-38.

LIU Shun-xi,WU Cai-fang. Study on fractal characteristics of different scales pore coal reservoir in Bide-Santang Basin[J]. Coal Science and Technology, 2016(2): 33-38.

[25] 吴中伟. 高性能混凝土-绿色混凝土[J]. 混凝土与水泥制品, 2000(1): 3-6.

WU Zhong-wei. High performance concrete-green concrete[J]. Chinal Concrete and Cement Products, 2000(1): 3-6.

[26] 尹红宇. 混凝土孔结构的分形特征研究[D]. 广西大学, 2006.

YIN Hong-yu. Study the fractal characteristic of concrete’spore structure[D]. Guangxi University, 2006.

[27] 郭剑飞. 混凝土孔结构与强度关系理论研究[D]. 杭州: 浙江大学, 2004.

GUO Jian-fei. The theoretical research of the pore structure and strength of concrete[D]. Hangzhou: Zhejiang University, 2004.

[28] 齐丽娜, 张 博, 王战凯. 最大类间方差法在图像处理中的应用[J]. 无线电工程, 2006(7): 25-26.

QI Li-na, ZHANG Bo, WANG Zhan-kai. Application of the OTSU method in image processing[J]. Radio Engineering of China, 2006(7): 25-26.

[29] Nirupam Sarkar, CHAUDHURI B B. An efficient differential box-counting approach to compute fractal dimension of image[J]. IEEE Transactions on Systems Man & Cybernetics, 1994, 24(1): 115-120.

[30] 孙寅森, 郭少斌. 基于图像分析技术的页岩微观孔隙特征定性及定量表征[J]. 地球科学进展, 2016(7): 751-763.

SUN Yin-sen,GUO Shao-bin. Qualitative and quantitative characterization of shale microscopic pore characteristics based on image analysis technology[J]. Advances in Earth Science, 2016(7): 751-763.

Cross scale correlation characteristics of pore structure and meso parameters of filling body

HU Jian-hua, JIANG Quan, REN Qi-fan, DING Xiao-tian

(College of resources and safety engineering, Central South University, Changsha 410083, China)

Abstract: Pore structure characteristics of filling bodies directly influence the mechanical features of the filling materials, which is the foundation of the multi-scale mechanics study of the filling bodies. On the basis of stereology and fractal theory, filling bodies pore structure SEM images was utilized, OTSU method and box counting method were used to calculate the filling body pore structure fractal dimension. The quantitative characterizations of pore structure of filling materials were obtained to analyze the correlations between fractal dimension and uniaxial compressive strength, moisture content, porosity and other meso parameters of filling bodies. Then the cross scale correlation between SEM quantitative image analysis and meso parameters of filling bodies were analyzed. The results show that the micro pore structure fractal dimension of filling bodies can characterize the complexity of filling body pore structure; a certain relationship exists between the fractal dimension of pore structure and the meso parameters of filling bodies, fractal dimension has a negative correlation with the uniaxial compressive strength, while there is a positive correlation between fractal dimension and water content; the correlation curves between pore structure characteristics fractal dimension and uniaxial compressive strength and water content are established, the association eigenvalue mean variances are obtained, the fractal dimension and uniaxial compressive strength mean square deviations is 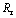=-0.638, while the value of fractal dimension and water content is 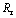=0.604.

Key words: filling body; fractal dimension; pore structure; correlation

Foundation item: Project(41672298) supported by the National Natural Science Foundation of China; Project (2017YFC0602901) supported by the National Key Research and Development Program of China

Received date: 2018-03-28; Accepted date: 2018-05-31

Corresponding author: HU Jian-hua; Tel: +86-13787056402; E-mail: hujh21@csu.edu.cn

(编辑  王  超)

基金项目：国家自然科学基金资助项目(41672298)；国家重点研发计划资助项目(2017YFC0602901)

收稿日期：2018-03-28；修订日期：2018-05-31

通信作者：胡建华，教授，博士；电话：13787056402；E-mail: hujh21@csu.edu.cn