考虑执行机构动态的WMR轨迹跟踪与镇定统一控制

韩光信

(吉林化工学院 信息与控制工程学院，吉林省 吉林市，132022)

摘要：轮式移动机器人的动力源于电机的驱动。研究将执行结构动态考虑在内的非完整轮式移动机器人的轨迹跟踪与镇定统一控制问题，即用一个控制器完成机器人的轨迹跟踪与镇定2种控制任务。基于运动学模型的跟踪控制律，利用李雅普诺夫稳定性理论及Backstepping技术，将运动学控制律推广到动力学模型。进一步将驱动电机的动态考虑在内，通过对跟踪控制律的修正，可以实现镇定控制任务，最后给出典型轨迹跟踪及镇定控制的仿真结果。

关键词：轮式移动机器人；执行机构动态；轨迹跟踪；镇定；统一控制

中图分类号：TP273          文献标志码：A         文章编号：1672-7207(2011)S1-0579-05

Trajectory tracking and stabilization unified control for nonholonomic WMRs considering actuator dynamics

HAN Guang-xin

(College of Information and Control Engineering, Jilin Institute of Chemical Technology, Jilin 132022, China)

Abstract: The power of wheeled mobile robots comes from the driving torque of the motor. The trajectory tracking and stabilization unified control problem for a nonholonomic wheeled mobile robot considering actuator dynamics were studied. On the basis of Lyapunov method and backstepping technique, tracking control law obtained using kinematics model was backstepped into the dynamic model. The strategy could be extended to point stabilization task through considering the actuator and the amendment of tracking control law. Finally, simulation results for typical trajectory tracking and stabilization control assignments were presented.

Key words: wheeled mobile robot; actuator dynamics; trajectory tracking; point stabilization; unified control

众所周知，轮式移动机器人属于典型的非完整系统^[1]。虽然非完整约束限制了机器人的瞬时运动，但是它们在位姿空间上仍然是全局可控的，这一独特性质使得设计反馈控制器具有挑战性。现有的移动机器人有履带式、腿式、轮式以及轮腿式移动机构，轮式移动机器人在机械设计上非常成熟，所以，在各种实用的移动机器人中以轮式移动机器人最为常见^[2]。目前，机器人的运动控制研究都是基于机器人的运动学模型或者动力学模型进行的，没有考虑机器人驱动电机的动态特性。相对于其他类型的执行机构，电机的特性比较复杂，如果在设计控制规律将其动态特性忽略，在实际实施时系统的性能可能会退化。Lozlowski等^[3-5]考虑驱动电机动态的问题，但是他们研究的都是机器人的轨迹跟踪问题，其中Lozlowski等^[3]的结果存在稳态误差，Tamoghna等^[4]考虑的是电感为零的简化情形，而Andre等^[5]研究的是四轮全向机器人的轨迹跟踪。另外，由于轮式移动机器人在任意平衡点的线性近似都是不可控的，所以，机器人的轨迹跟踪控制问题与镇定控制问题是分别研究的。当机器人需要在这2种任务之间进行转换时，就需要进行控制器的切换，因此，最好用1个控制器可以同时用于轨迹跟踪与镇定2种任务^[2]。基于以上考虑，本文作者考虑机器人的动力学模型以及驱动电机的动态特性，研究其轨迹跟踪与镇定统一控制问题。利用李雅普诺夫方法及Backstepping技术，首先将运动学轨迹跟踪控制律推广到动力学模型，然后将驱动电机的动态考虑在 内，进一步将跟踪控制律进行适当修正后用于镇定控制任务，最后给出典型轨迹跟踪与镇定控制任务的仿真结果。

1  机器人的动力学模型及执行机构

动态特性

图1所示为笛卡儿坐标系下的轮式移动机器人。假设质心位于后轮轴的中点上，WMR可由以下非线性微分方程来描述^[6]：

           (1)

图1  机器人示意图

Fig.1  Schematic figure of wheeled mobile robots

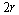其中：；m和I分别为WMR的质量与转动惯量；为后轮轴的长度；为后轮的直径；为质心坐标；为车身相对于X轴正向的方向角；为相对于垂直轴的角速度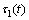；与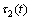分别是右后轮和左后轮电机所提供的驱动力矩。轮子只能滚动不能侧向滑动的非完整约束可以描述为：

下面考虑执行机构的动态^[3]。假设2个后轮的驱动电机都是直流的，且电机产生的力矩与电流成正比，则：

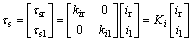
其中：和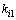为比例系数。电刷输入电压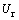和与电感和，电阻和及反电动势的关系可由方程(2)描述：

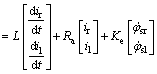          (2)

其中：和为反电动势系数；和为电机的转速。考虑到一般的机器人都安装有减速齿轮，电机转速和机器人的线速度与角速度的关系为：

其中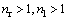：均为减速比。则式(2)可整理为：

      (3)

同时，电流和轮子产生的力矩之间的关系也要修正为：

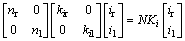      (4)

2  轨迹跟踪与镇定统一控制律设计

设和分别表示期望的位置和方向角，和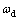表示线速度及角速度。假设和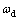及其各阶导数均有界。对于机器人的运动学模型，定义旋转误差状态向量^[7]：

       (5)

将误差变量和分别对时间取微分，易得运动学误差动态方程为：

           (6)

若规定期望方向角及跟踪方向角的表示范围为，则式(5)中的变换矩阵为非奇异矩阵，因此，就等价于

，

即 。

下面首先设计轨迹跟踪控制律，然后将其适当扩展后用之完成镇定控制任务。

2.1  轨迹跟踪控制律

选取Lyapunov函数：

        (7)

其中。显然V₁是正定的，并且只有当时，V₁=0。将V₁对时间微分得：

根据反步法^[8]，取虚拟速度控制输入为^[9]：

  (8)

则有：

即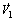是负半定的。另外，由式(7)易知的下边界为0，所以，会收敛到一个有限值，由此可知，，和都是有界的。沿由式(6)和式(8)组成的闭环系统的二阶导数为：

根据假设条件及上面结果可知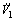：是有界的，从而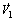是一致连续的；由Barbalat引理^[8]可知：当时，，因此，和都会收敛到平衡点。同理由和的收敛性及Barbalat引理可以证明：也会收敛到平衡点。

如果与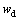不同时等于0，即满足持续激励条件时，式(6)在平衡点线性化系统中才是可控的，也就是说，当时，式(6)在平衡点的线性化系统中将失去控性。为了使得控制律式(8)对所有的与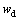都有意义，并为下一步将跟踪控制律扩展到镇定控制任务打下基础，需要进行速度标定^[10]，即取，，，其中与均为大于0的常数。需要说明的是，速度标定后，前述论述过程同样成立。

下面利用反步法将动力学及执行机构动态特性考虑在内。定义虚拟速度输入与实际速度输入之间的误差为：，。则

对于式(1)描述的动力学系统，令，，易知。选取一级增广李氏函数为：

其对时间的微分为：

其中：

选取虚拟力矩输入为

；

则：

利用前面的推导，易知。引入力矩输入误差：

得到：

定义二级李氏函数为：

则：

为便于观察，将上式后2项写成向量相乘的形式为：

其中：

选取

                                       (9)                                           

则：

根据的表达式，易知其下确界为0，且为负半定的，则必有界且趋向于某一有限值，因此，，和都是有界的。容易验证也是有界的，所以由Barbalat引理可知，当时，。也就是说，，，， 。

2.2  镇定控制律

镇定控制就是将机器人从一个初始状态控制到任意给定的目标状态上，由于机器人的运动路线事先不能确定，所以，通常假设机器人工作在无障碍的环境 中。但是，除了在生产线上工作的运输机器人外，大部分机器人都要工作在有障碍的环境中，所以，机器人首先要规划出一条可行路径，然后沿该路径运动到目标点上。为不失一般性，设定目标状态为 ，由轨迹跟踪控制律的设计前提可知(与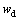不能同时等于0)，前面的轨迹跟踪控制律不能直接用于镇定控制任务，需要适当修正。具体策略是使机器人跟踪一条通过目标点的轨迹，这样，镇定控制问题就可以按轨迹跟踪问题来处理^[10]，前提是要保证参考机器人本身能够渐进稳定在给定目标点上，此时可取

             (10)

其中：，。利用前面设计的轨迹跟踪控制律就可以完成镇定控制任务，同时采用文献[9]中的方法可以证明闭环系统的渐进稳定性。

3  仿真结果

取机器人的物理参数为： I=2 kg·m²， ，驱动电机的参数取自文献[4]。假设机器人跟踪一条圆形轨迹： 。仿真时参数取为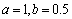，机器人的初始姿态。镇定控制选取为并行泊车任务，机器人的初始位姿为(x(0), y(0), φ(0))=(0, 8, 0)。图2所示为跟踪轨迹，图3和图4所示分别为右轮和左轮驱动电压输入，容易看出机器人能在较短的时间内跟上期望轨迹。图5所示为并行泊车的仿真结果，运动路线非常圆滑。

图2  跟踪轨迹

Fig.2  Tracking trajectory

图3  右轮驱动电压U_r

Fig.3  Voltage input of right driving wheel

图4  左轮驱动电压U_l

Fig.4  Voltage input of left driving wheel

图5  并行泊车路线

Fig.4  Voltage input of parallel driving wheel

4  结论

移动机器人的动力都是由安装在驱动轮轴上的驱动电机提供的，本文将执行结构动态考虑在内，研究了非完整轮式移动机器人的轨迹跟踪与镇定统一控制问题。首先基于运动学模型设计轨迹跟踪控制律，利用李雅普诺夫方法及Backstepping技术，将运动学控制律推广到动力学模型，进一步将驱动电机的动态考虑在内，然后将跟踪控制律加以扩展，使其能同时用于镇定控制任务，最后以典型的轨迹跟踪及镇定控制任务为例给出了仿真结果。

参考文献：

[1] Kolmanovsky I, McClamroch N H. Developments in nonholonomic control problems[J]. IEEE Control Systems Magazine, 1995, 15(6): 20-35.

[2] 韩光信, 陈虹, 马苗苗, 等. 约束非完整轮式移动机器人轨迹跟踪的非线性预测控制[J]. 吉林大学学报: 工学版, 2009, 39( 1): 177-181.
Han Guang-xin, Chen Hong, Ma Miao-miao, et al. Nonlinear model predictive control of trajectory tracking for nonholonomic mobile robots with constraints[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(1): 177-181.

[3] Lozlowski K, Majchrzak J. A backstepping approach to control a nonholonomic mobile robot[C]// Proceedings of the 2002 IEEE International Conference on Robotics & Automation. Washington D C, 2002: 3972-3977.

[4] Tamoghna D, Indra N K. Design an implementation of an adaptive fuzzy logic-based controller for wheeled mobile robots [J]. IEEE Transactions on Control Systems Technology, 2006, 14(3): 501-510.

[5] Andre S C, Moreira A P, Paulo J C. A nonlinear model predictive control strategy for trajectory tracking of a four-wheeled omnidirectional mobile robot[J]. Optimal Control Application and Methods, 2007, 29: 335-352.

[6] Corradini M L, Orlando G. Control of mobile robots with uncertainties in the dynamical model: A discrete time sliding model approach with experimental result[J]. Control Engineering Practice, 2002, 10:23-34.

[7] Kanayama Y, Kimura Y, Miyazaki F, et al. A stable tracking control method for an autonomous mobile robot[C]// Proceedings of IEEE Conference on Robotics and Automation. Cincinnati, 1990: 384-389.

[8] Krstic, M, Kanellakopoulos I, Kokotovic P. Nonlinear and Adaptive Control Design[M]. New York: John Wiley & Sons Inc, 1995.

[9] Pourboghrat, F, Karlsson, M P. Adaptive control of dynamic mobile robots with nonholonomic constraints[J]. Computers and Electrical Engineering, 2002, 28: 241-253.

[10] Canudas de W C, Khennouf H, Samson C, et al. Nonlinear Control Design for Mobile Robots[C]// Zheng Y F. Recent trends in mobile robots. Hackensack: World Scientific, 1993: 121-156.

(编辑 何运斌)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：吉林省教育厅科技规划项目(2008-350)

通信作者：韩光信(1971-)，男，吉林舒兰人，教授，从事移动机器人控制、约束系统的控制、预测控制等研究；电话：0432-63083112；E-mail: hangeorge517@163.com