基于模糊预测控制的机车制动控制方法
刘剑锋1, 2，刘友梅2，桂卫华1，刘豫湘2，黄志武1
(1. 中南大学 信息科学与工程学院，湖南 长沙，410075；
2. 南车株洲电力机车有限公司，湖南 株洲，412001)
摘 要：为了减少模型参数、噪声耦合和随机性干扰对机车制动控制系统控制精度和稳定性的影响，提出1种基于模糊预测控制的制动控制方法，利用基于满意度的T-S模糊建模方法建立精确的预测模型。研究结果表明：通过模糊遗传算法进行滚动优化，获得全局最优解作为预测控制控制器的输出，进而提高系统控制快速性和稳定性，仿真结果验证了该方法的有效性。
关键词：预测控制；T-S模糊模型；模糊遗传算法；机车制动控制系统
中图分类号：TP273 文献标识码：A 文章编号：1672-7207(2009)05-1329-07
Locomotive brake control method based on fuzzy predictive control
LIU Jian-feng1, 2, LIU You-mei2, GUI Wei-hua1, LIU Yu-xiang2, HUANG Zhi-wu1
(1.School of Information Science and Engineering, Central South University, Changsha 410075, China;
2. China South Locomotive and Rolling Zhuzhou Electric Locomotive Co. Ltd., Zhuzhou 412001, China)
Abstract: In order to reduce the influence of the model parameters, the noise coupling and the random interference on the control precision and stability of the locomotive brake control system, a brake control method based on fuzzy predictive control was proposed. The precise predictive model was built by using T-S fuzzy modeling based on the conception of character satisfaction degree, and the fuzzy genetic algorithm was used as rolling optimization method. The results show that using the brake control method, the global optimal solution can be obtained, which is used as the controller output. Therefore, it can improve the control speed and stability of this system. This improved method is effective.
Key words: predictive control; T-S fuzzy model; fuzzy genetic algorithm; locomotive brake control system
机车制动控制系统是列车安全运行的关键设备，列车进行制动时，由主控机车给从控机车发送制动命令及目标压力等信息，各从控机车接到信号后，通过各自的机车制动系统对整列车辆实施空气制动。研究结果表明，机车制动系统的控制实时性、精度和稳定性将关系着整个列车的制动性能和制动安全。由于列车编组增长、质量增大，给列车的制动控制带来了很多新问题。如对于2万t列车，其整车长度大约为2 km，列车管长度也将达到2 km。同时，由于空气制动波速无法超过300 m/s，使得在常用、紧急制动时，列车纵向冲动急剧增大，可能造成严重的断钩、脱轨事故。因此，必须采取有效的方法，对长大列车制动系统进行快速、精确和稳定的控制。针对机车制动系统这样一类具有非线性、时变性和迟滞特性的控制对象，以及对于制动控制实时性、精度和稳定性方面的要求，不少研究者进行了研究，如余世明等[1]针对有约束多目标多自由度预测控制问题，提出了1种既适合于参数模型又适合于非参数模型的在线优化策略；张晓 婕[2]给出了1种多变量时变系统的CRAMA模型近似解耦法；宋春跃等[3]提出了递阶变时域滚动优化生产控制策略，使模型失配、时变、干扰等引起的不确定性能及时得到弥补；牛东晓等[4]利用支持向量机和遗传算法提出了1种可以对高负荷状态下的系统进行预测的方法；周富强等[5]提出1种解析数学模型结合神经网络校正模型的计算方法建立冷连轧机轧制力预报模型。模型预测控制方法综合利用实时信息和模型信息，对目标函数不断进行滚动优化，并根据实际测得的对象输出修正或补偿预测模型，适用于复杂的工业过程，主要包括3个部分[6]：预测模型、反馈校正和滚动优化。在此，本文作者通过分析机车制动控制系统的动态过程，同时考虑机车制动控制系统控制对象特性与各影响因素之间的关系，提出1种机车制动控制方法。该方法是在模型预测控制的基础上，利用基于满意度的T-S模糊模型作为预测模型，采用模糊遗传算法来进行滚动优化。最后，对该控制方法进行仿真分析，并在具体工程中进行应用。
1 制动影响因素分析
影响机车制动系统的因素有：
a. 制动系统各部件机械和气路特性参数的误差。这些差异直接导致制动系统控制特性产生差异。
b. 元器件老化变形等都有可能使气路管道产生泄漏，从而降低制动控制的精度。
c. 在实际系统中，机车总风缸压力并不是一个恒值(保持在600~800 kPa)，特别是在充放气的过程中，给控制系统带来扰动，影响控制的稳定性。
基于上述分析，要实现列车的精确、快速制动，必须采取先进的控制算法来消除这些因素的影响。
2 T-S模糊建模
由于机车制动控制系统是一类具有非线性、时变性和迟滞特性的控制对象，用传统的方法难以得到气缸压力变化的精确数学模型。T-S模型是1种能方便地用于预测控制的预测模型，在此，本文作者提出1种基于满意度的T-S模糊模型用于提高预测模型的稳定性与精度。首先，使用模糊聚类方法对参数进行初始化，并采用反向传播算法离线辨识出模型的前件参数；然后，采用带遗忘因子的递推最小二乘法辨识模型后件参数，同时，引入系统品质满意度，在线调整遗忘因子，从而提高模型的精度和逼近速度。
2.1 T-S模糊模型结构
T-S模型将输入变量空间划分为c个模糊子空间,即包含c条规则，对于每一个模糊子空间，系统的局部模型可用1个线性方程来描述，而系统的总输出则为各局部线性模型输出加权和[7]。
对于MISO的非线性控制系统，其T-S模型的一般形式为：
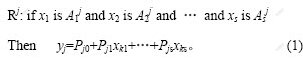
模糊集合的隶属度函数定义为高斯乘积函数：
应用加权平均法解模糊，被控系统的总输出为：
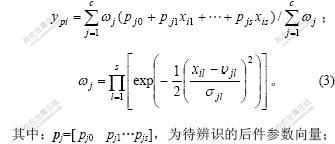
2.2 基于满意度的T-S模糊模型的参数辨识
系统模型的前件参数可以通过BP算法学习得到，由于BP算法容易陷入局部最优[8]，因此，模糊系统参数的初始化非常重要。采用模糊C平均聚类方法(FCM)初始化模糊规则的前件参数υj和σj会尽可能地避免BP算法陷入局部最优。
对具有时变特性或严重非线性并且在大操作范围内工作的被控对象，很难用离线模型非常精确地逼近系统动态，因此，需要通过在线修正后件参数pj来提高模型的辨识精度。
在实际生产过程中，往往对系统的控制性能如逼近时间、超调量等提出了一定的要求，因此，将最小二乘中的遗忘因子l设计为1个可调参数，根据系统的满意度在线调节l，使辨识的模型能够更加快速、稳定地逼近实际工况。调节规律可以用下式表示：
根据μt，在λmin和λmax之间按照一定的指数规律调整λ，改变遗忘因子。其调节规律可以描述为：系统为正作用时，满意度μt反映影响规则的主要因素，若满意度减小，则说明超调量太大，上升时间短，则增大λ，系统对当前数据的学习能力减弱，规则参数基本保持不变；若满意度增大，则说明系统输出超调量小，上升时间长，可以减小λ，系统对当前数据学习能力加强，加快模型的逼近程度。
3 基于模糊遗传算法的滚动优化方法
通过对基于满意度的T-S模糊建模方法的分析，可以得到1个较精确的系统模型。但由于机车制动系统存在管路泄漏和随机扰动等影响因素，会对系统控制精度和稳定性造成影响，因此，有必要提高滚动优化的精度，同时，增强系统稳定性。遗传算法就是1种广泛应用的寻优算法。
3.1 模糊遗传算法
遗传算法[12](Genetic algorithm，简称GA)是1种并行随机搜索最优化方法。应用遗传算法寻求最优解问题一般包含3个基本操作：复制、交叉(交叉结果为Pc)和变异(变异结果为Pm)。其中交叉和变异是2个关键操作，对于保证GA的寻优过程能够收敛到全局最优值，以及提高寻优过程的收敛速度起着重要的作用。
研究表明：影响Pc和Pm的因素除了适应度函数值之外，还有当前的遗传代数(CN)以及最大适应度函数值保持不变的代数(Kg)。因此，CN和Kg都是模糊量，难以用精确量表示。为了实现Pc和Pm的自适应调整，通过隶属度函数建立精确量输入与模糊变量的模糊映射关系[9-10]，再进行模糊推理与清晰化，即模糊决策，实现精确量输出，得到Pc和Pm。
3.2 模糊遗传算法参数的确定
3.2.1 输入变量与输出变量的量化
输入变量为CN/N和Kg/N(N为总进化代数)，变化范围分别为(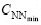
，
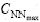)和(
，
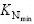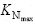)；输出变量为Pc和Pm，变化范围分别为(
，
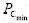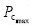)和(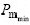
，
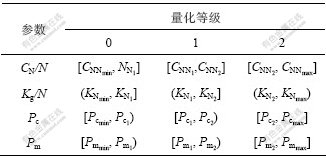
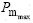)。同时，根据制动气压的变化特性，即气压误差小、中、大3种情况，把系统变量的量化等级为3级：[0，1，2]，采用均匀量化。
变量的量化情况如表1所示。其中：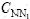
和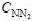
是CN/N的中间值；
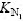和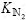
是Kg/N的中间值；
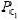和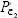
是Pc的中间值；
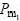和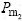
是Pm的中间值。
表1 模糊变量的量化值
Table 1 Quantized value of fuzzy variables
3.2.2 模糊集合的隶属度值和模糊推理规则
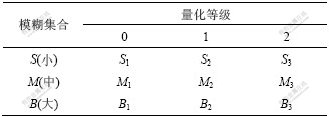
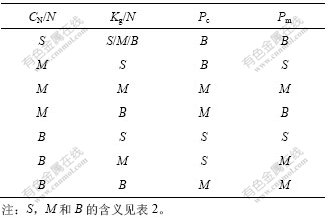
对于输入变量CN/N，Kg/N和输出变量Pc和Pm，采用数值方法描述它们模糊集合的隶属度函数，如表2所示。其中：S1，M1和B1是量化等级为0时，模糊集合S(小)，M(中)和B(大)对应的3个遗传算子；S2，M2和B2是量化等级为1时，模糊集合S，M和B对应的3个遗传算子；S3，M3和B3是量化等级为2时，模糊集合S，M和B对应的3个遗传算子。
表2 模糊集合的隶属度
Table 2 Membership value of fuzzy sets
在系统中表现为：CN很小时，说明进化刚开始，应该采用较大的Pc和Pm，从而加大搜索范围，保持群体的多样性；当CN很大时，说明进化接近尾声，应采用较小的Pc和Pm，以防止破坏优良个体。当Kg/N很小时，说明寻优刚取得突破，Pc和Pm应适当减小；当Kg/N较大时，说明寻优进展缓慢，Pc和Pm应该调大，加强搜索。因此，根据以上对影响遗传操作算子调整因素的模糊分析，可以得到在遗传进化过程中对遗传算子调整的模糊推理规则，如表3所示。
表3 模糊推理规则
Table 3 Fuzzy inference rule
以上通过模糊推理得到的是模糊量，而对于实际的控制则必须为清晰量，因此，可以采用重心法将模糊量Pc和Pm转换成相应的清晰量。
3.3 个体评价方法
在机车制动控制系统中，k时刻的优化性能指标选用含有系统输出对期望值误差和控制增量加权值的二次型目标函数的最小值，具体为：
把式(10)作为个体评价方法。下面采用模糊遗传算法进行滚动优化，得到全局最优的控制量输出。
4 改进的机车制动控制方法
通过上述分析，利用基于满意度的T-S模糊建模建立预测模型，增强控制模型的精度；采用模糊遗传算法进行滚动优化，提高控制算法的精度，最后，得到如图1所示的控制器框图。
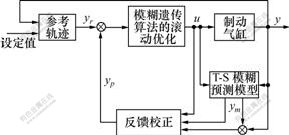
图1 改进的机车制动控制原理框图
Fig.1 Principle diagram of improved locomotive brake control
其具体流程如下。
Step 1：由系统要求获取未来的期望输出序列yr(k+i)。
Step 2：执行带遗忘因子的最小二乘递推算法，估计参数A(s-1)，B(s-1)，C(s-1)和D(s-1)。
Step 3：利用递推优化算法[11]得到最优值ym。
Step 4：经过在线反馈校正得到系统的实际预测输出值yp(k+i)= ym(k+i)+ωe(k)。其中ω为补偿系数，根据实际的运行效果进行调整；e(k)是包括不可测定的外界干扰在内的实际输出y(k)和预测模型输出ym(k)之间的误差。
Step 5：利用式(10)确定个体评价方法。
Step 6：设计遗传算子并确定其运行参数。使用模糊规则确定遗传算子，确定终止进化代数N，并用重心法计算得到Pc和Pm。
Step 7：充分利用Δu(k+1), Δu(k+2), …, Δu(k+l-1)有用信息，减少预测误差、噪声干扰等因素影响，改善控制效果，利用平滑滤波作用的输入加权控制率：
Step 8：采用模糊遗传算法滚动优化，获得控制的最优序列u(k+i-1)。
Step 9：将第1控制量u(k)作用于系统，返回。
5 仿真分析以及实际应用效果
5.1 实验数据处理及参数的选取
为了验证本文所提出的改进的模糊预测控制方法，先将其应用于机车制动控制系统的仿真研究，仿真工具为MATLAB6.5[12]。
现场采集数据1 200组，数据采集周期为20 ms，共剔除50组数据。对剩余的数据进行标准化处理，将得到的1 150组标准数据分为2份，其中：900组作为训练样本用来训练T-S模型，另外250组数据作为测试样本，用于检验模型的预测能力。
在本系统中，控制量u是脉宽调制的占空比，系统输出y是气缸压力。根据采集到的数据，建立气缸压力的T-S模糊模型，模糊规则数C=5，BP学习中学习次数为40，学习率a=0.001[13]。
在广义预测控制中，控制参数的选取至关重要。在实验中，考虑到控制系统的实时性要求，在满足控制效果的前提下，选取较小的N和M以减少计算量，取N=5，M=1，控制加权系数l取0.1[14]。
5.2 模糊遗传算法的滚动优化方法仿真分析
根据前面所描述的流程进行仿真。通过大量实验，各变量参数选取如表4所示。
表4 参数设置
Table 4 Parameters setting
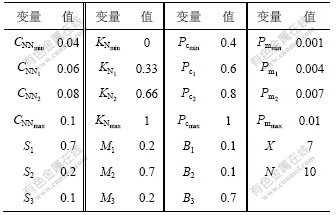
图2和图3所示为分别采用典型的滚动优化算法和基于模糊遗传算法的滚动优化方法时控制器输出值和当前误差值之间的比较结果。当输出为正时，开充气阀，输出为负时，开放气阀。系统中采用PWM调制控制阀门的开关，开关的周期为20 ms。从图2和图3可以看出，采用本文所提出的方法基本上可以追踪系统的实时变化，达到精确控制。同时，所提出的方法在收敛速度上比原有方法的快，高速开关阀的动作次数减少2/3左右，阀的使用寿命延长。
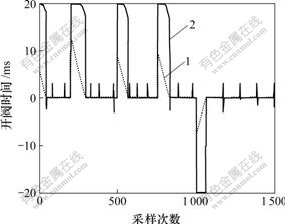
1—当前误差值；2—控制器输出
图2 典型的滚动优化方法仿真结果
Fig.2 Simulated results of representative rolling optimization method
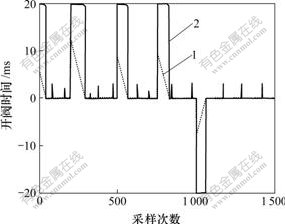
1—当前误差值；2—控制器输出
图3 基于模糊遗传算法的仿真结果
Fig.3 Simulated results of fuzzy genetic algorithm
5.3 改进的模糊预测控制算法的应用
图4所示是利用广义预测控制算法得到的系统实际输出值和目标值之间的比较结果；图5所示是利用本文提出的算法得到的系统实际输出值和目标值之间的比较结果。
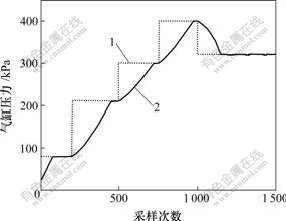
1—目标值；2—采样值
图4 典型的滚动优化方法控制效果
Fig.4 Control effects of representative rolling optimization method
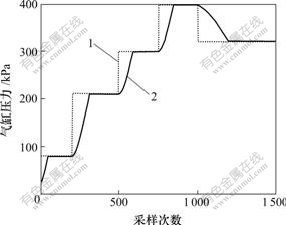
1—目标值；2—采样值
图5 基于模糊预测控制算法的控制效果
Fig.5 Control effects based on fuzzy predictive control algorithm
从图4和图5可见，本文提出的算法在控制过程中相对于目标值的误差更小，可控误差低于1 kPa，尤其是快要达到目标值以及稳定之后的过程中，基本不会出现气压过充、过放和不稳定的情况。因此，本文提出的算法要优于典型的广义预测控制算法，系统控制的精度可满足制动系统的技术指标(均衡风缸误差为±1 kPa，闸缸为±2 kPa)。同时，本文提出的算法其调节速度比典型算法的调节速度快2倍，还可以有效地抑制系统的随机扰动，满足制动系统的技术指标。
6 结论
a. 针对我国目前新型列车机车制动控制系统这类非线性系统，引入系统品质满意度的概念，建立了系统的 T-S模糊模型。
b. 采用基于模糊遗传算法的滚动优化方法来求取系统的全局最优控制器输出值，使预测输出更准确，开关阀的动作次数可以减少2/3左右。
c. 与传统方法相比较，采用改进的机车制动控制方法建立的预测模型准确且有较强的鲁棒性，系统的控制精度、响应速度和稳定性均提高，在实际测试中调节速度提高2倍。
参考文献：
[1] 余世明, 杜 维. 目标规划法在预测控制滚动优化及在线辨识中的应用[J]. 自动化学报, 2002, 28(11): 995-1000.
YU Shi-ming, DU Wei. Application of goal programming in receding-horizon optimization and online identification of predictive control[J]. Acta Automatic Sinica, 2002, 28(11): 995-1000.
[2] 张晓婕. 多变量时变系统的CRAMA模型近似解耦法[J]. 中国计量学院学报, 2004, 15(4): 284-286.
ZHANG Xiao-jie. An approximate decoupling method applicable to multivariable time-changing systems with the CARMA model[J]. Journal of China Institute of Metrology, 2004, 15(4): 284-286.
[3] 宋春跃, 李 平. 混杂生产系统变时域滚动优化生产控制[J]. 浙江大学学报, 2005, 39(12): 1954-1958.
SONG Chun-yue, LI Ping. Varying receding-horizon based production control for hybrid production systems[J]. Journal of Zhejiang University: Engineering Science, 2005, 39(12): 1954-1958.
[4] 牛东晓, 刘 达, 陈广娟. 基于遗传优化的支持向量机小时负荷滚动预测[J]. 电工技术学报, 2007, 22(6): 148-152.
NIU Dong-xiao, LIU Da, CHEN Guang-juan. Support vector machine models optimized by genetic algorithm for hourly load rolling forecasting[J]. Transactions of China Electrotechnical Society, 2007, 22(6): 148-152.
[5] 周富强, 曹建国, 张 杰, 等. 基于神经网络的冷连轧机轧制力预报模型[J]. 中南大学学报: 自然科学版, 2006, 37(6): 1155-1160.
ZHOU Fu-qiang, CAO Jian-guo, ZHANG Jie, et al. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models[J]. Journal of Central South University: Science and Technology, 2006, 37(6): 1155-1160.
[6] 席裕庚. 预测控制[M]. 北京: 国防工业出版社, 1993.
XI Yu-geng. Predictive control[M]. Beijing: Defense Industry Press, 1993.
[7] XU Yong, CHEN Zeng-qiang, YUAN Zhu-zhi. Design of Takagi-Sugeno fuzzy model based nonlinear sliding model controller[J]. Journal of Systems Engineering and Electronics, 2005, 16(4): 78-83.
[8] 林海军, 齐丽彬, 张礼勇. 基于BP神经网络的模拟电路故障诊断研究[J]. 电测与仪表, 2007, 44(12): 41-43.
LIN Hai-jun, QI Li-bin, ZHANG Li-yong. Research for analogous circuit fault diagnosis based on BP neural network[J]. Electrical Measurement & Instrumentation, 2007, 44(12): 41-43.
[9] 高 异, 杨延西, 刘 军. 模糊遗传滚动优化的LS-SVM预测控制研究[J]. 系统仿真学报, 2007, 19(3): 1227-1280.
GAO Yi, YANG Yan-xi, LIU Jun. Research on LS-SVM predictive control using fuzzy genetic algorithm rolling optimization[J]. Journal of System Simulation, 2007, 19(3): 1227-1280.
[10] 李富明, 朱云龙, 尹朝万, 等. 基于模糊遗传算法的模糊调度研究[J]. 信息与控制, 2004, 33(12): 703-707.
LI Fu-ming, ZHU Yun-long, YIN Chao-wan. Study on the fuzzy scheduling based on the fuzzy genetic algorithms[J]. Information and Control, 2004, 33(12): 703-707.
[11] SU Bai-li, CHEN Zeng-qiang, YUAN Zhu-zhi. Constrained predictive control based on T-S fuzzy model for nonlinear systems[J]. Journal of Systems Engineering and Electronics, 2007, 18(1): 95-100.
[12] Chen Z Q, Lin X, Sun Q L, et al. A novel fuzzy predictive functional control based on T-S fuzzy model[C]//Proceedings of Chinese Control Conference. Sanya, 2006: 1204-1208.
[13] Wang S B, Hu P H, Lin L. Study and stability analysis of state feedback predictive control based on fuzzy inference[C]// Proceedings of the Sixth World Congress on Intelligent Control and Automation, WCICA’06. 2006: 1007-1011.
[14] Guzman J L, Berenguel M, Dormido S. Interactive teaching of constrained generalized predictive control[J]. IEEE Control Systems Magazine, 2005, 25(2): 52-66.
收稿日期：2008-09-06；修回日期：2009-01-06
基金项目：国家自然科学基金重点资助项目(60634020)
通信作者：刘剑锋(1977-)，男，湖南涟源人，博士，讲师，从事智能控制、网络控制等研究；电话：0731-82655576；E-mail: ljf@mail.csu.edu.cn
