Neural adaptive PSD decoupling controller and its application in three-phase electrode adjusting system of submerged arc furnace
来源期刊:中南大学学报(英文版)2013年第2期
论文作者:HE Jian-jun(贺建军) 刘郁乔 喻寿益 桂卫华
文章页码:405 - 412
Key words:PSD algorithm; decoupling controller; submerged arc furnace; three phase electrode
Abstract: Taking three-phase electrode adjusting system of submerged arc furnace as study object which has nonlinear, time-variant, multivariable and strong coupling features, a neural adaptive PSD(proportion, sum and differential) dispersive decoupling controller was developed by combining neural adaptive PSD algorithm with dispersive decoupling network. In this work, the production technology process and control difficulties of submerged arc furnace were simply introduced, the necessity of establishing a neural adaptive PSD dispersive decoupling controller was discussed, the design method and the implementation steps of the controller are expounded in detail, and the block diagram of the controlled system is presented. By comparison with experimental results of the conventional PID controller and the adaptive PSD controller, the decoupling ability, adaptive ability, self-learning ability and robustness of the neural adaptive PSD dispersive decoupling controller have been testified effectively. The controller is applicable to the three-phase electrode adjusting system of submerged arc furnace, and it will play an important role for achieving the power balance of three-phrase electrodes, saving energy and reducing consumption in the process of smelting.
J. Cent. South Univ. (2013) 20: 405–412
DOI: 10.1007/s11771-013-1501-3
HE Jian-jun(贺建军), LIU Yu-qiao(刘郁乔), YU Shou-yi(喻寿益), GUI Wei-hua(桂卫华)
School of Information Science and Engineering, Central South University, Changsha 410083, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2013
Central South University Press and Springer-Verlag Berlin Heidelberg 2013
Abstract: Taking three-phase electrode adjusting system of submerged arc furnace as study object which has nonlinear, time-variant, multivariable and strong coupling features, a neural adaptive PSD(proportion, sum and differential) dispersive decoupling controller was developed by combining neural adaptive PSD algorithm with dispersive decoupling network. In this work, the production technology process and control difficulties of submerged arc furnace were simply introduced, the necessity of establishing a neural adaptive PSD dispersive decoupling controller was discussed, the design method and the implementation steps of the controller are expounded in detail, and the block diagram of the controlled system is presented. By comparison with experimental results of the conventional PID controller and the adaptive PSD controller, the decoupling ability, adaptive ability, self-learning ability and robustness of the neural adaptive PSD dispersive decoupling controller have been testified effectively. The controller is applicable to the three-phase electrode adjusting system of submerged arc furnace, and it will play an important role for achieving the power balance of three-phrase electrodes, saving energy and reducing consumption in the process of smelting.
Key words: PSD algorithm; decoupling controller; submerged arc furnace; three phase electrode
1 Introduction
Submerged arc furnace is widely used in smelting iron-alloy product as an arc resistance furnace. The current is transferred into the furnace through three-phase electrode, thereafter, the furnace can produce arcing resistance heat to heat up raw materials, since chemical reduction reactions should be taken place under certain temperature. Otherwise, furnace load is relevant to the distance between the foot of the electrode and metal pool. To get the best refining outcome, the three-phase power balance, in the smelting process, must be maintained by adjusting the position of the three-phase electrode whose inserted depth directly affects the electrode current [1].
Owing to the complexity of industrial smelting process, three-phase electrode adjusting system of submerged arc furnace has following characteristics.
1) nonlinearity: adjusting the three-phase electrode movement, the control system can change the size of arc resistance. The electric arc is a complicated nonlinear phenomenon which is difficult to be precisely described by an mathematical model.
2) multiple variables and strong coupling: owing to the feature of three-phase circuit, when disturbances occur in a single phase voltage or current, the other two phase circuit voltages and currents will be affected as well.
3) time variability: the dynamic characteristic of the circuit parameter varies with working conditions.
4) severe disturbances: there are many disturbance factors which can affect the system, such as the resistance of metal pool, the ingredient and humidity of raw material, electrode paste quality, smelting condition and heating surface and so on.
At present, the inserted position of the electrode [2] is adjusted by the conventional PID (proportion, integral and differential) controller. However, it is not easy to modify the controller parameters online and the controller has no decoupling function. Moreover, the method of electrode adjustment is not suitable for real-time working condition because it is hard to reach the three-phase power balance and unable to meet the requirement of control, even worse, the system will be unsteady. Therefore, in this work, a neural adaptive PSD dispersive decoupling controller was proposed to meet the operating characteristics of three-phase electrode adjusting system of submerged arc furnace. A large number of simulation experiments show that the new control system has good dynamic performance and robustness, which means the proposed design is feasible and effective in practical application.
2 Design of neural adaptive PSD decoupling control system
2.1 Adaptive PSD control algorithm
Generally, process parameters first need to be identified, and then the adaptive control law can be established. Due to the nonlinearity and time variation of three-phase electrode adjusting system of submerged arc furnace, it is difficult to ensure the accuracy of the mathematical model derived from the identification. The mechanism of the adaptive control algorithms without direct parameter identification [3], proposed by Marsik and Strejic, is that the adaptive PSD control law can be formed according to the objective function established by the geometric characteristic of process error. This method does not need to identify process parameters, because it will form adaptive control law as long as the expected output and the actual one are monitored online. Thus, this kind of adaptive controller is simple and easy to realize.
The adaptive PSD control law adopts incremental digital output [4], its mathematical expression is
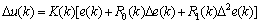 (1)
(1)
where K(k) is the controller gain, 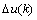 is the controller output increment, R0(k) is the proportional coefficient, R1(k) is the differential coefficient. Apart from this, e(k), De(k) and D2e(k) are process error, the first-order and second-order differential of errors, respectively. PSD incremental control law is designed to ensure that three absolute average values of proportion, sum and differential are equal, that is
is the controller output increment, R0(k) is the proportional coefficient, R1(k) is the differential coefficient. Apart from this, e(k), De(k) and D2e(k) are process error, the first-order and second-order differential of errors, respectively. PSD incremental control law is designed to ensure that three absolute average values of proportion, sum and differential are equal, that is
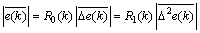 (2)
(2)
Let  , and
, and 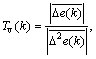 so,
so,
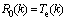 ,
,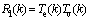 (3)
(3)
The iterative algorithm [5] of the increments △Te(k) and △Tv(k) is
 (4)
(4)
 (5)
(5)
where  is a constant,
is a constant, 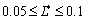 , when Te=2Tv, Te and Tv are optimal proportions, then the control law is
, when Te=2Tv, Te and Tv are optimal proportions, then the control law is
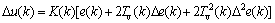 (6)
(6)
Marsik and STREJIC [3] presented the adaptive algorithm of gain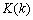 , whose recursion formula is
, whose recursion formula is
when 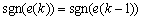 ,
,
 (7)
(7)
where 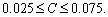
when 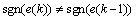 ,
,
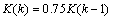 (8)
(8)
The meaning of this algorithm is that when the sign of error is always the same, that is, continuously deviates from the given value, and the gain K(k) can automatically increase to adjust the output value to match with the given value as soon as possible; when the sign of error is different, this means that outputs swing in the vicinity of the given value, the gain K(k) can decrease automatically, adjust output carefully and make it consistent with the given value.
2.2 Neural adaptive PSD controller
In neuron PID controller [6], the gain K is the most sensitive parameter. As K changes, three items, namely P, I and D change at the same time. Therefore, how to choose the value of K would have a great effect on the performance of neural control system. It has been proved that when the value of K is larger, the system response will be faster, but the overshoot increases, on the other side. On the contrary, when K is smaller, system response will be slower, and the overshoot correspondingly decreases, but when the value of K is extremely small, the steady-state error will exist in the response of system.
Because three-phase electrode adjusting system of submerged arc furnace has features like nonlinearity, time variability, multiple variables, strong coupling and severe disturbance, the characteristics of system change easily. Thus, a value of K should be designed to change according to the variations of control object features. Due to those features of three-phase electrode adjusting system, a neural adaptive PSD controller combining the adaptive PSD algorithm with neuron PID controller is developed [7]. The control principle is shown in Fig. 1.
This controller use neural learning algorithm to adaptively adjust weight 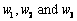 , and use the PSD adaptive algorithm to adjust the value of gain K at the same time. This neural adaptive PSD controller adopts supervised Hebb leaning rule, and the algorithm is described as follows:
, and use the PSD adaptive algorithm to adjust the value of gain K at the same time. This neural adaptive PSD controller adopts supervised Hebb leaning rule, and the algorithm is described as follows:
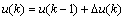 (9)
(9)
Let threshold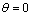 , then
, then
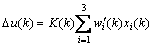 (10)
(10)
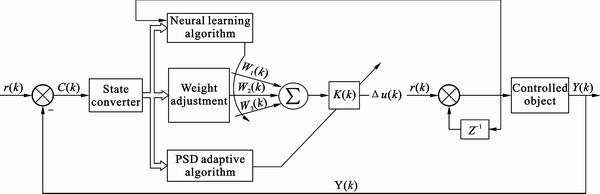
Fig. 1 Structure of neural adaptive PSD control system
where
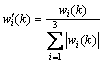 (11)
(11)
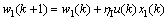 (12)
(12)
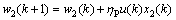 (13)
(13)
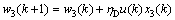 (14)
(14)
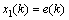 is the system error, equivalent to integral.
is the system error, equivalent to integral.
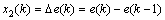 is the change of the system error, equivalent to proportion.
is the change of the system error, equivalent to proportion.
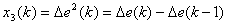 is the first-order differential of the system error change, equivalent to differential.
is the first-order differential of the system error change, equivalent to differential.
K(k) is computed according to Eqs. (7) and (8) .
hI, hP and hD are the integral learning rate, the proportion learning rate and the differential learning rate, respectively.
Because an automatic gain K(k) adjusting method used in adaptive PSD algorithm is introduced into the neuron PID control algorithm which has been shown above, thus, the self-learning ability, self-organization ability and robustness of this control algorithm are improved significantly.
2.3 Neural network dispersive decoupling controller
As the three-phase electrode adjusting system has strong coupling characteristic, only improving the controller performance cannot get ideal control result. Therefore, a neural network dispersive decoupling controller [8] is introduced to solve this problem. This kind of dispersive decoupling controller is composed of n×(n–1)SISO(single input single output) neural networks (n is the number of inputs). The whole decoupling target of control system is allocated to every
neural subnet, respectively. So, this controller has following several features: 1) every neural subnet, decoupling to one interference channel, is a single input and single output system and therefore the index-functions are simple and easy to implement; 2) does not change the main channel characteristics of the generalized object; 3) what several neural subnets learn at the same time and parallelly process can short learning time; 4) eliminate the mutual interference of single MIMO (multiple input multiple output) neural network in the decoupling learning process, and improve the decoupling control result.
A typical double input and double output controlled process is cited to explain the control principle of dispersive decoupling network, the schematic diagram of dispersive decoupling network is shown in Fig. 2 [9].
The neural network dispersive decoupling controllers ND1 and ND2 are the dynamic time-delay neural network (TDNN), every network has an input terminal and output terminal. Two delay links (TDL) provide the input and output delay signals to the network terminal respectively [10]. Considering a three-layer neural network, the output layer is one node. The activation function of the hidden layer neurons adopts
hyperbolic tangent function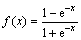 , and the output layer is a linear function. The outputs of ND1 and ND2 can be described as below.
, and the output layer is a linear function. The outputs of ND1 and ND2 can be described as below.
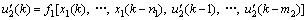 (15)
(15)
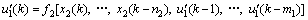 (16)
(16)
where 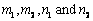 are positive integers, which can be approximated according to the order of controlled process.
are positive integers, which can be approximated according to the order of controlled process.
For the neural network dispersive decoupling controller, as shown in the Fig. 2, the error of the actual output and the expected output should be taken as the objective function, but the output of the dispersive decoupling network is unknown. To avoid the contradiction, the dispersive decoupling controller and the controlled object need to be regarded as a generalized object, and only in this way can the system output error be taken as the objective function of the neural network, that is:
The objective function [11] of neural network decoupling controller ND1 is
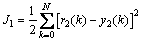 (17)
(17)
The objective function of neural network decoupling controller ND2 is
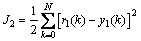 (18)
(18)
Using dynamic BP (back-propagation) algorithm, the weight updating in network is decided by the following equation.
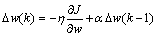 (19)
(19)
where h is the learning rate, a is the momentum factor, N is the sampling number in the training.
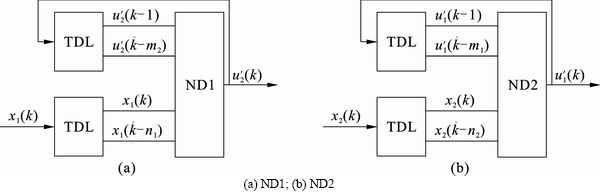
Fig. 2 Schematic diagrams of dispersive decoupling network:
So, the weight updating equations of ND1 and ND2 are expressed respectively as
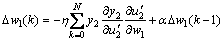 (20)
(20)
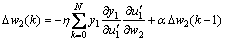 (21)
(21)
For convenient discussing, the subscripts of variables are neglected, then the Eqs. (20) and (21) are expressed together as
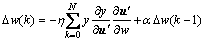 (22)
(22)
The sign of the partial derivative is expressed as
is expressed as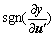 , through the adjusting learning rate
, through the adjusting learning rate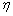 , let
, let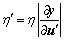 , then, the Eq. (22) can be written as
, then, the Eq. (22) can be written as
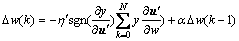 (23)
(23)
If y increases monotonely with u', then 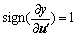 , on the contrary,
, on the contrary, 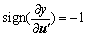 .
.
The relationship of the input and output in the net can be described as
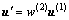 (24)
(24)
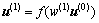 (25)
(25)
where u' is the output signal of output layer, u(1) is the output signal of hidden layer, 
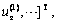
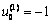 ,
, 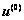 is the input signal of input layer,
is the input signal of input layer, 
 w(2) is the connection weight vector between the hidden layer and output layer,
w(2) is the connection weight vector between the hidden layer and output layer, 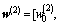
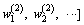 w(1) is the connection weight vector between the input layer and hidden layer.
w(1) is the connection weight vector between the input layer and hidden layer.
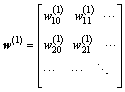
The neural network decoupling controller is trained by simplified BP algorithm. To the neural network’s output layer, the equation is shown as
 (26)
(26)
The equation for the hidden layer is
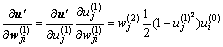 (27)
(27)
Substituting Eqs. (26) and (27) into Eq. (23), the updating weight expression can be gotten for the output and hidden layer.
In the output layer,
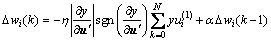 (28)
(28)
In the hidden layer,
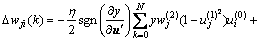
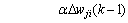 (29)
(29)
In conclusion, the algorithm of the neural network decoupling control has following steps:
1) Neural network decoupling controllers ND1, ND2 and the controlled process are connected in series.
2) all the initial weights of the decoupling controllers are set in the range of [–1, 1] randomly.
3) The input signals are given to make the output signals of the controller correspond with the decoupling input signals.
4) Calculating the output of neural network u', u(1), u(0) through Eqs. (24) and (25). After that, given N numbers of the process variable  changes along with the time, until u' reaches the training number which has been set (in the beginning, u'=0)
changes along with the time, until u' reaches the training number which has been set (in the beginning, u'=0)
5) Calculating the weight changes of the output layer and hidden layer through Eqs. (28) and (29), and then updating the weight.
6) Repeating steps (3)–(5) until the system reaches the given iteration times.
2.4 Neural adaptive PSD dispersive decoupling control system
The neural adaptive PSD dispersive decoupling control system combines neural adaptive PSD controller with neural network dispersive decoupler, whose structure is shown in Fig. 3.
In Fig. 3, the neural adaptive PSD controller can adjust the value of K and the parameters P, I and D to adapt to the changes of the contorlled object in real time, and neural network dispersive decoupler can realize decoupling control on line. Therefore, the neural adaptive PSD dispersive decoupling controller can overcome the severe coupling and other control problems which cannot be solved by a single neural adaptive PSD controller used in a multivariable coupling system. it can also overcome the adaptive adjusting parameter problem which cannot be solved by the single dispersive decoupling controller used in the time-variation controlled object. In addition, the neural adaptive PSD control just has one neuron, so it has simple structure and short learning process; the dispersive decoupler supports parallel training of multiple subnets, and it can greatly shorten the learning time to solve the difficulty that the neural network controller has poor real-time performance.
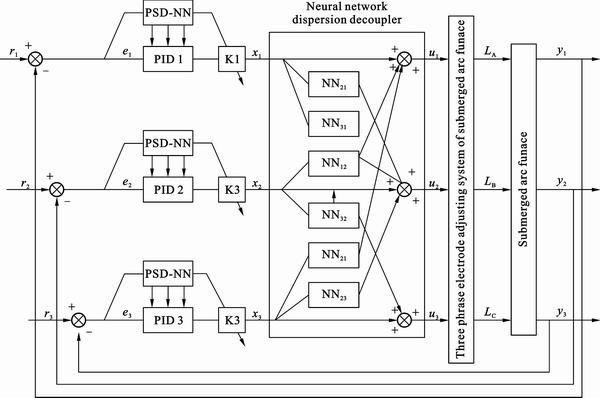
Fig. 3 Structure of neural adaptive PSD dispersive decoupling control system
3 Simulation experiment
In this work, the research object is a 30 000 kW Si-Mn submerged arc furnace in a ferroalloy factory. The controlled parameters are the three-phase currents of the electrodes [12]. The structure of the control system is shown in Fig. 4.
In Fig. 4, IA, IB and IC denote the current of A-phase, B-phase and C-phase electrodes, respectively. IAS, IBS and ICS denote the given current values of three-phase electrodes, respectively. LA, LB and LC denote insertion depth of three-phase electrodes, respectively.
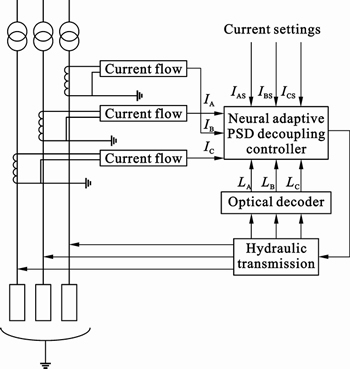
Fig. 4 Schematic diagram of three-phase electrode adjusting system of submerged arc furnace
The controller adjusts the lift of electrodes through hydraulic transmission to maintain the constant electrode currents in the smelting process. The simulation experiments are conducted in order to illustrate the control effect of the neural adaptive PSD dispersive decoupling controller in the three-phase electrode adjusting system. Currently, the location-current model [13–14] is regarded as the more mature model of the submerged arc furnace, so constant current control strategy is still used in the simulation research. After collecting a large amounts of data and equipment parameters in the production field, the current-location mathematical model of the submerged arc furnace is established as follows:

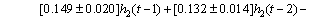
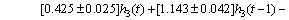
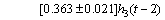 (30)
(30)
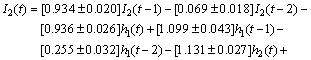
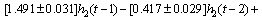
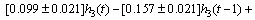
 (31)
(31)
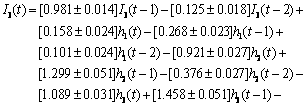
 (32)
(32)
In these equations, the values before the sign “±” represent the average values of parameters, and the values after the sign “±” represent the upper and lower limits of identified parameters.
It can be seen that when the insertion depth of one phase electrode of the three-phase electrode changes, the currents of the other two-phase electrode will also change at the same time. Therefore, the system has strong coupling feature.
Taking MATLAB as the simulation platform [15], using the identified electrode location-current model, adopting the lower limits of the model parameters, setting the initial values of PID (P=0.4, I=0.2, and D=0.4), setting the initial value of K (K=0.006), initializing randomly the weights between 0 and 1, and letting IAS = 4 kA, IBS = 5 kA, ICS = 6 kA. Figure 5 shows the responsing processes of the control system.
For easy comparison, a simulation curve of digital PID control and a simulation curve of neural adaptive PSD control without dispersive decoupler are plotted in these figures. The curve 1 represents neural adaptive PSD dispersive decoupling control result, the curve 2 represents the control result of the neural adaptive PSD and the curve 3 represents control result of the conventional PID. It can be seen that the neural adaptive PSD controller is much better than PID controller. After the introduction of dispersive decoupler,the system overshoot further decreases largely and the settling time is significantly shortened and the dynamic response is further improved. The control system shows good adaptability and robustness of the proposed design.
Because the dynamic characteristics of circuit parameters of the submerged arc furnace vary with industrial operation condition, the model parameters are adjusted to the upper limits without changing the parameters of controller, just for illustrating the adaptive performance of the controller. Figure 6 shows the simulation results.
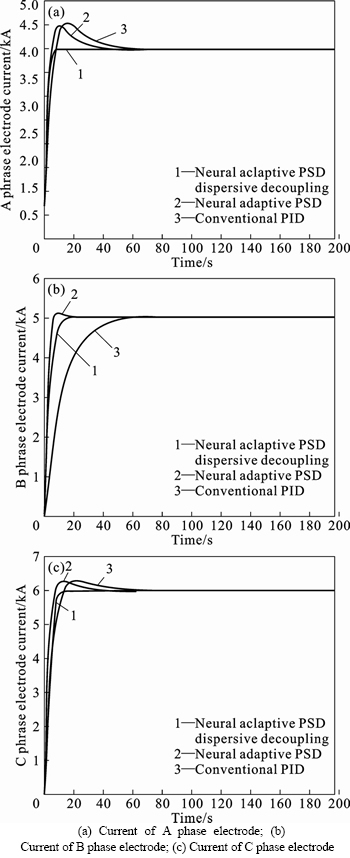
Fig. 5 Response curves of three-phase electrode currents:
It can be seen that conventional PID control cannot adjust controller parameters according to the controlled object on line. So, it leads to bigger overshoot and longer settling time of the system. The neural adaptive PSD dispersive decoupling controller can adaptively adjust controller parameters according to the object change, so it can still have good control results.
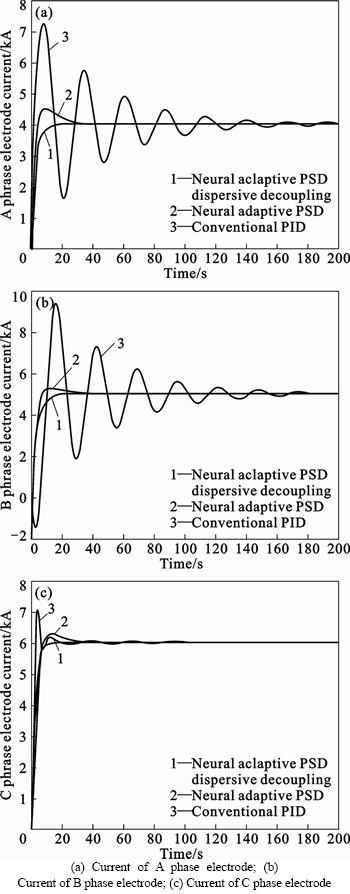
Fig. 6 Response curves of three-phase electrode currents with parameters changed:
4 Conclusions
The three-phase electrode adjusting system of submerged arc furnace is difficult to be established accurate mathematical model because of its features such as nonlinearity, time variability, multiple variables and strong coupling. The control system can achieve good control effects with the help of the method of neural adaptive PSD dispersive decoupling control. This method can effectively improve the dynamic performance and eliminate the coupling effect among variables. It has four following remarkable characteristics: 1) it is able to identify the controller parameters according to the inputs and outputs of the generalized system and does not rely on the accurate mathematical model of the controlled system; 2) it has simple structure and clear physical significance; 3) this method has online learning function, so it can overcome the effect of the time-variant parameter in the controlled system, and the learning time is short and parameter convergence is rapid; 4) This method has strong adaptive ability and good decoupling performance. Therefore, the neural adaptive PSD dispersive decoupling control method has broad application prospects in three-phase electrode adjusting system of the submerged arc furnace.
References
[1] LI Meng-ji, ZHANG Feng. Electric balance control of the three phases power in smelting region in the sub-merged furnace of the ferroalloys [J]. Ferro-alloys, 2003, 34(5): 22–23. (in Chinese)
[2] WANG Bing-jin. On PID control system design of electrode regulation of submerged arc furnace [J]. Ferro-alloys, 2009, 40(1): 38–40. (in Chinese)
[3] MARSIK J, STREJIC V. A new conception of digital adaptive PSD control [J]. Problem of Control and Information Theory, 1993, 12(44): 267–279.
[4] ALEXIK, MIKULAS. Simulation experiments with self tuning PSD control algorithm [C]// Proceedings of UK Sim 10th International Conference on Computer Modelling and Simulation, Cambridge, UK, 2008: 34–39.
[5] JIAO Bin, GU Xin-sheng. Improvement and realization of neuron PSD control in servo-control system [J]. Journal of Shanghai Jiaotong University (Science), 2005, 10(2): 143–146.
[6] SHU Huai-lin. PID neural network for decoupling control of strong coupling multivariable time-delay systems [J]. Control Theory and Applications, 1998, 15(6): 920–924. (in Chinese)
[7] ARDEHALI M M, SABOORI M, TTESHNELAB M. Numerical simulation and analysis of fuzzy PID and PSD control methodologies as dynamic energy efficiency measures [J]. Energy Conversion and Management, 2004, 45(13): 1981–1992.
[8] ZHOU Hong, ZHONG Ming-hui. A neural intellectual decoupling control strategy for a power plant ball miller [J]. International Journal of Automation and Computing. 2005, 2(1): 43–47.
[9] SUN Jian-hua, WANG Wei, ZHENG Ke-wei. Research of PID neural networks decoupling control of marine nuclear power plant [J]. Journal of Harbin Engineering University, 2007, 28(6): 656–659.
[10] LI Ming, LIN Yong-jun, MA Yong-guang. Adaptive neural non-model decouple control for MIMO system[J]. 2003, 20(3): 68–71. (in Chinese)
[11] LIU Guo-hai, LIU Ping-yuan, SHEN Yue, WANG Fu-liang. Neural network generalized inverse decoupling control of two-motor variable frequency speed-regulating system [J]. Proceedings of the CSEE, 2008, 28(36): 98–102
[12] MULHOLAND A C, BRERETON-STILES P J, HOCKADAY C J. The effectiveness of current control of submerged arc furnace electrode Penetration in selected scenarios [J]. Journal of The South African Institute of Mining and Metallurgy, 2009, 109(10): 601–607
[13] HAUKSDOTTIR A S, GESTSSON A. Current control of a three-phase submerged arc ferrosilicon furnace [J]. Control Engineering Practice, 2002, 10(4): 457–463.
[14] HAUKSDOTTIR A S, SODERSTROM T, THORFINNSSON Y P, GESTSSON A. system identification of a three-phase submerged arc ferrosilicon furnace [J]. IEEE Transactions on Control Systems Technology, 1995, 3(4): 377–387.
[15] ZHOU Huang-bin, ZHOU Yong-hua, ZHU Li-juan. Implementation and comparison of improving BP neural network based on MATLAB [J]. Computing Technology and Automation, 2008, 27(1): 28–31.
(Edited by HE Yun-bin)
Foundation item: Project(61174132) supported by the National Natural Science Foundation of China; Project(09JJ6098) supported by the Natural Science Foundation of Hunan Province, China
Received date: 2012–03–31; Accepted date: 2012–09–10
Corresponding author: He Jian-jun, Professor; Tel: +86–13507465056; E-mail: jjhe@csu.edu.cn

