DOI：10.19476/j.ysxb.1004.0609.2019.03.10

镁合金中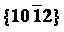、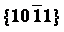两种孪晶界面的可动性比较

李  亨¹，刘  钊¹，张  真2，彭金华²

(1. 合肥工业大学 工业与装备技术研究院，合肥 230009；

2. 合肥工业大学 材料科学与工程学院，合肥 230009)

摘  要：形变孪生是镁合金的主要塑性变形方式之一，镁合金的两种主要孪晶为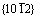、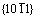孪晶，两种常见孪晶在形貌上存在较大的差异。本文采用分子动力学模拟与微观组织实验观察相结合的手段，研究了两种孪晶压缩过程的应力应变曲线、微观结构以及界面的迁移方式，对比分析两种孪晶界面的可动性。并且从原子运动以及位错滑移的角度，解释两者存在差异的原因。结果表明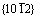：孪晶界迁移所需的应力较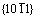孪晶界迁移所需的应力低，并且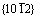孪晶界的迁移呈现“弓形”方式，而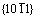孪晶界以“台阶”的方式进行迁移。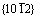孪晶界的迁移是B/P面相互转变的过程，因而界面更容易大范围、高速率地迁移；而透射电镜(TEM)观察和模拟结果均显示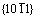，孪晶界面上存在周期性的界面位错，阻碍了孪晶界的移动，并且需有基面位错滑移至孪晶界面处堆积，为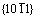孪晶界的迁移提供能量。

关键词：镁合金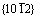；孪晶；孪晶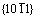；孪晶界面可动性；分子动力学模拟

文章编号：1004-0609(2019)-03-0508-09　　     中图分类号：TG146　　     文献标志码：A

镁合金由于具有质量轻、比强度高、切削性能好、易于回收等优异的性能，在3C电子产品、新能源汽车零部件、航空航天等领域有着广泛的应用前景^[1-3]。然而由于其室温塑性较差，成为限制镁合金更为广泛应用的一个重要因素。由于镁合金具有密排六方晶体结构，其对称性较低，在室温条件下独立滑移系较少，不能满足均匀变形需要5个独立滑移系的要求，因而孪生作为一种特殊的塑性变形机制，在镁合金塑性加工中起着重要的作用^[4-6]。镁合金中有两种主要的孪晶类型，即拉伸孪晶和压缩孪晶^[7-8]。其中，拉伸孪晶多形成于非基面取向的晶粒中，该类孪晶一旦形成就会迅速扩展，并逐渐吞噬基体，因而该类型孪晶的形貌特征多呈现透镜状，如图1(a)所示；而压缩孪晶则多形成于基面取向的晶粒中，这类孪晶形成后，难以发生横向扩展，因而此类孪晶的形貌特征多呈现窄片状，如图1(b)所示，在低温变形过程的较高应变阶段，此类孪晶非常常见。以往研究者针对这两类孪晶的研究，主要以经典的孪生位错理论^[9-11]为基础，探讨孪生诱导的微观组织及织构演变规律^[12-20]，以及孪晶对材料力学性能的影响^[21-24]，这些研究都较为全面。而目前研究很少涉及从原子尺度分析孪生的晶体学过程，以及不同界面原子结构对界面可动性的影响。关于这个问题的研究，对于理解镁合金中两种孪晶的不同动力学行为及其对力学性能的影响，有着重要的理论指导作用。

因此，本文利用分子动力学模拟的手段，研究了镁合金中常见的两种孪晶的界面可动性，分析了两种孪晶界的迁移方式存在差异的原因。并利用透射电镜(TEM)观察和分析了孪晶的形貌特征以及孪晶界的迁移规律。

1  模拟方法

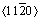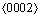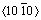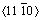为了比较两种孪晶界面的可动性，构建了两种长方体模型，其中一种为孪晶，即模型内预置了一条孪晶界，如图2(a)所示；另一种为孪晶，即预置了一条孪晶界，如图2(b)所示。两种模型的右侧晶粒的取向(c轴)相互垂直，即X轴都指向方向，孪晶模型的Y轴指向方向，Z轴指向方向，而孪晶模型的Y轴指向方向，Z轴指向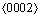方向。两种模型的左侧晶粒的取向，分别与右侧晶粒构成相应的孪晶模型。两种模型大小一致，均为10 nm×40 nm×20 nm，体系的原子总数均在38万个左右。图中斜插的白色原子代表孪晶界原子，红色原子代表内部的HCP原子，而灰色原子代表在施压过程中的固定层原子。模拟过程中X、Y、Z三个方向均采用自由边界条件，并且采用Sun解析的嵌入式EAM势函数^[25]来描述原子间相互作用。两个体系首先在300 K下自由弛豫1万步，待达到平衡后，沿Z轴压缩，压缩过程中保持下层原子(Bottom layer)不动，而上层原子(Top layer)以每步向下移动0.02 nm。本文采用LAMMPS软件^[26]进行模拟分析，大量的模拟研究数据已经证实了该软件的可靠性。

图1  镁合金金相组织

Fig. 1  Metallographs of magnesium alloy

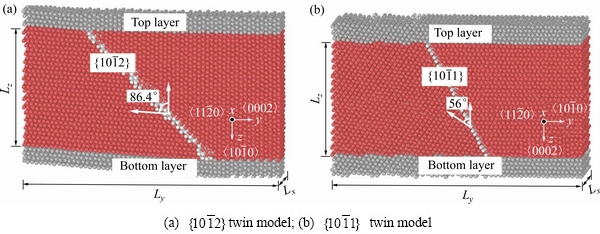
图2  金属镁的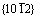、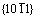孪晶模型

Fig. 2  Twin computational models of Mg

2  实验

本文所用的实验材料为中铝洛阳铜业有限公司提供的AZ31合金铸轧板(名义成分(质量分数)：2.8% Al、0.88% Zn、0.2% Mn、0.0031% Fe、0.001% Ni、0.001% Cu)。铸轧板材的原始厚度为6.5 mm，宽度为600 mm。将原始铸轧板进行430 ℃、2 h均匀化退火并冷却后，再次加热至375 ℃并保温5 min，在完成对轧辊的预热后，进行单道次变形量为10%和20%的热轧。轧辊直径157 mm，转速18 r/min。

金相样品选取轧板侧面作为观察面，用酚醛树脂进行镶样，经400^#、600^#、800^#砂纸手工研磨，机械抛光后，用醋酸苦味酸腐蚀晶界，在Leica EC3金相显微镜下观察组织形貌。TEM实验同样选择热轧板的侧面作为样品观察面，首先将样品机械研磨到厚度为0.2 mm以下，再冲制成3 mm圆片，利用电解抛光的方式制备观察样品，在JEOL 2100型透射电镜进行观察，加速电压为200 kV。

3  模拟结果

从晶体学角度分析，HCP结构中的面和面的原子排列存在差异，所以面和面作为孪晶界面时，由于界面原子排列的不同，也导致了两者的可动性以及迁移方式存在差异。

3.1  应力应变曲线分析

探究两种孪晶界面可动性的差异可通过对比分析两者的应力应变曲线。如图3所示，使用模拟数据拟合两种模型的应力应变曲线。黑色曲线代表孪晶模型，红色曲线代表孪晶模型。对比两条曲线发现，在初始变形阶段(应变ε≤ 2.9%)，两条曲线较吻合，之后两条曲线开始出现差异。结合两种孪晶界面的迁移情况，分析如下。

本文采用OVITO软件^[27]进行可视化分析。如图4所示，选取了几组典型的状态对比图，其中图4(a)所示代表孪晶的模型结构，图4(b)所示代表孪晶的模型结构。图4(a₁)和4(b₁)所示为两种模型充分弛豫后的初始模型(step=0)。对比发现，孪晶界为一条直线，而孪晶界是一条折线(图中黄色折线)，并且偏离了理想的孪晶界面。目前，大量的实验结果也表明孪晶界存在偏离理想孪晶界的现象^[28]，孪晶界是由BP面、PB面以及界面组成^[28-29]，与本文模型吻合，说明了本文模型的合理性。

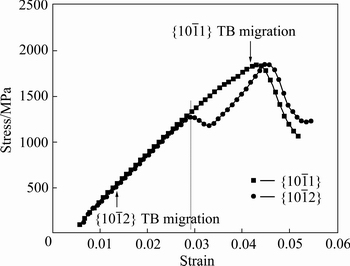
图3  两种模型应力-应变曲线

Fig. 3  Stress-strain curves of two models

图4  压缩过程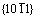、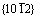孪晶模型微观结构变化

Fig. 4  Microstructures of twin model in compression process

图4(a₂)和4(b₂)所示表示两种模型在第13步的状态图。此时，图4(b₂)中的孪晶界开始迁移，由原来的黄色折线位置迁移到白色原子的位置，而图4(a₂)中的孪晶界仍保持不动。结合图3的应力应变曲线可知，在第13步(ε=1.3%)时，孪晶模型对应的应力为σ=508 MPa，此时孪晶界开始迁移。

图4(a₃)和4(b₃)所示表示两种模型在第43步的状态图。此时，图4(b₃)中的孪晶界已迁移出边界，而图4(a₃)中的孪晶界刚开始迁移，但也只是在界面右下角小范围的移动，如图4(a₃)的黄色虚线区域，而不像孪晶界的大范围整体迁移，说明孪晶界的可动性更好。同样结合图3的应力-应变曲线，在第43步(ε=4.2%)时，孪晶模型对应的应力为σ=1835 MPa，此时孪晶界开始迁移。对比两条孪晶界的迁移情况以及相应的应力状态可知，孪晶界更早也更容易迁移，并且孪晶界是大范围迁移，而孪晶界的迁移是小范围的移动。

3.2  孪晶界迁移方式分析

如图5(a)和(b)所示，对比两条孪晶界迁移之后的结构可知，孪晶界的迁移是以台阶的方式进行的(由图5(a)中的黄色虚线迁移至蓝色虚线位置)，最后形成曲折的孪晶界，台阶有三到四个原子层厚度，所以孪晶界的这种迁移方式范围较小并且也限制了界面的迁移速率。而如图5(b)所示，孪晶界的迁移是以弓形的方式进行的，这种弓形长大的方式也说明了孪晶界可以实现大范围、高速率的迁移。

4  分析讨论

4.1 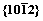孪晶界可动性分析

上述模拟结果表明孪晶界的迁移是以弓形方式进行的，实际上孪晶界的迁移是B/P面转变的过程。如图6(a)所示，利用OVITO可视化软件先标记右侧晶粒的{0002}基面原子(深蓝色)和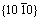柱面原子(黄色)，白色原子表示孪晶界面原子。观察孪晶界沿图中黄色箭头迁移的过程中标记原子的变化情况。由图6(b)可知，当孪晶界扫过标记原子，原基面原子(深蓝色)变成了柱面原子(深蓝色)，而同样地，原柱面原子(黄色)变成了基面原子(黄色)。说明在孪晶界迁移过程中，晶粒的基面和柱面发生了相互转换，所以孪晶界的迁移实际上是B/P面的转变过程。

如图7(a)所示，给出了HCP结构镁(ABAB……方式堆垛)的{0002}基面与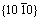柱面的原子排列示意图。图7(a)是沿不同的方向观察两个面的原子排列，对比可知，基面与柱面具有相似性，所以易于实现两者之间的相互转换。

图5  孪晶界面迁移方式

Fig. 5  Migration mode of twin boundary

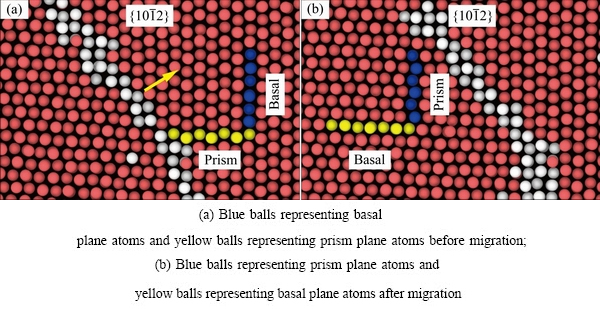
图6 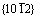 孪晶界迁移过程B/P面转变

Fig. 6  Basal plane will translate into prism plane in 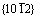 twin boundary migration process

图7  {0002}基面与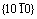柱面的原子排列示意图以及B/P面转变过程

Fig. 7  Process of surface transformation

如图7(a)中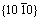柱面，红色线条上的原子与基面原子排列相似，只不过柱面上的原子并不在同一个平面上。如图7(b)简述了柱面原子排列转变为基面原子排列的过程。本文将该过程分为两步，第一步柱面上的B层原子沿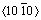方向运动，直到与柱面上的A层原子处于同一平面。第二步，处于同一平面上的A、B层原子相互排斥，沿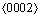方向运动达到基面的原子间距。至此即完成了柱面向基面的转变过程。

同理，基面向柱面的转变过程也可通过上述两步完成。整个转变过程说明了基面和柱面之间相互转变易于实现，也进一步说明了孪晶界的迁移易于实现。并且孪晶界是由BP面和界面组成的，故孪晶界的BP面也不稳定，易于实现B/P面转变，所以孪晶界容易开动，这也是孪晶界易迁移的原因之一。

4.2  孪晶界可动性分析

上述模拟结果表明孪晶界的迁移是以台阶的方式进行的。如图8(a)和(b)所示，运用OVITO的位错分析可以发现孪晶界上存在大量的周期性界面位错(其中图8(a)中的紫色实线代表位错线，图8(b)中的黄色箭头代表界面位错的柏氏矢量)，这些界面位错的柏氏矢量为b₁=1/27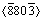。由此可知，该周期性的界面位错柏氏矢量并不在基体和孪晶的滑移面上，所以这些周期性的位错很难移动，起到了钉扎的作用，将孪晶界固定，需要较大的能量才能促使孪晶界迁移。图8(c)和(d)所示为孪晶的透射电镜图，其中图8(c)所示为暗场像，图8(d)所示为明场像。由图8(c)和(d)可以看出，在孪晶界面上存在大量周期性排列的小圆点，这些小圆点就是模拟结果所发现的周期性界面位错。

由于孪晶界的迁移需要较大的驱动力，所以在孪晶界迁移之前需要积累大量的能量。如图9(a)所示，在孪晶界迁移之前都会有基面位错在孪晶界处塞积，位错的柏氏矢量为b₂=1/3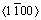，即基面的不全位错(图中的绿色原子表示位错滑过之后，形成的层错)。

如图9(b)，当基体的基面位错(黄色实线)运动到孪晶界，基面位错会与界面位错发生反应，形成位错之间的缠结、堆积，阻碍位错的进一步运动，导致位错的塞积，位错塞积处会产生应力集中，并积累足够的能量驱动孪晶界的迁移。然而，迁移的过程也只是在位错塞积处形成台阶，然后带动孪晶界的迁移。因此，孪晶界的迁移呈现小范围、低速率、台阶式的迁移方式。

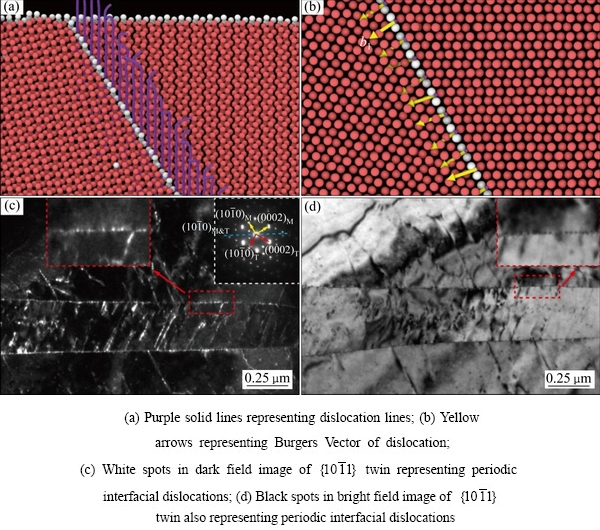
图8  孪晶界面上的周期性界面位错

Fig. 8  Periodic interfacial dislocations on 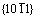 twin interface

图9  基面位错的滑移以及与界面位错的反应

Fig. 9  Basal dislocation spilling up at interface

5  结论

1) 孪晶界的迁移较孪晶界的迁移更容易。孪晶界开动的应力为σ=508 MPa，而孪晶界开动的应力为σ=1835 MPa。

2) 孪晶界的迁移是B/P面相互转换的过程，呈现大范围、高速率的弓形迁移方式。并且孪晶界是由BP面和界面组成的，而孪晶界的BP面易于转变，所以孪晶界不稳定容易开动。

3) 孪晶界的迁移呈现小范围、低速率、台阶式的迁移方式。孪晶界面上存在周期性的界面位错，起到钉扎作用，阻碍孪晶界的迁移。并且孪晶界的迁移过程是依靠基面位错在孪晶界处塞积，形成应力集中，驱动孪晶界迁移。

REFERENCES

[1] 刘 倩, 单忠德. 镁合金在汽车工业中的应用现状与发展趋势[J]. 铸造技术, 2007, 28(12):1668-1671.

LIU Qian, SHAN Zhong-de. Application and prospect of magnesium alloys in automotive industry[J]. Foundry Technology, 2007, 28(12): 1668-1671.

[2] ROBERT S B. Magnesium products design[M]. USA: The International Magnesium Association, 1987: 373-375.

[3] 丁文江. 镁合金科学与技术[M]. 北京: 科学出版社, 2007: 25-30.

DING Wen-jiang. Science and technology of magnesium alloys[M]. Beijing: Science Press, 2007: 25-30.

[4] DUDAMELL N V, ULACIA I, GALVEZ F, YI S, BOHLEN J, LETZIG D, HURTADOB I, PEREZ-PRADOA M T. Twinning and grain subdivision during dynamic deformation of a Mg AZ31 sheet alloy at room temperature[J]. Acta Mater, 2011, 59(18): 6949-6962.

[5] SANDLOBESS, ZAEFFERER S, SCHESTAKOW I, YI S, GONZALEZ-MARTINEZ R. On the role of non-basal deformation mechanisms for the ductility of Mg and Mg-Y alloys[J]. Acta Mater, 2011, 59(2): 429-439.

[6] ZHANG F, HAO M, WANG F C, TAN C W, YU X D, MA H L,CAI H N. Role of twinning and detwinning in the shock-hardening behavior of rolled Mg-3Al-1Zn alloy[J]. Scripta Mater, 2012, 67(12): 951-954.

[7] CHRISTIAN J W, MAHAJAN S. Deformation twinning[J]. Progress in Materials Science, 1995, 39(1): 1-157.

[8] YOO M H. Slip, twinning, and fracture in hexagonal close-packed metals[J]. Metallurgical Transactions A, 1981, 12(3): 409-418.

[9] 刘 庆. 镁合金塑性变形机理研究进展[J]. 金属学报, 2010, 46(11): 1458-1472.

LIU Qing. Research progress on plastic deformation mechanism of Mg alloys[J]. Acta Metall Sin, 2010, 46(11): 1458-1472.

[10] 单智伟, 刘博宇. Mg的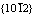形变孪晶机制[J]. 金属学报, 2016, 52(10): 1267-1278.

SHAN Zhi-wei, LIU Bo-yu. The mechanism of 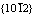deformation twinning in magnesium[J]. Acta Metall Sin, 2016, 52(10): 1267-1278.

[11] 涂 坚, 周志明, 柴林江, 黄 灿. 密排六方金属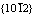形变孪晶长大机制的研究进展[J]. 中国有色金属学报, 2015, 25(9): 2317-2325.

TU Jian, ZHOU Zhi-ming, CHAI Lin-jiang, HUANG Can. Research progress on growth mechanism of 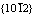twin in hexagonal close packed metals[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(9): 2317-2325.

[12] 汪炳叔, 邓丽萍, CHAPUIS A, 郭 宁, 李 强. AZ31镁合金在平面应变压缩过程中的孪生行为研究[J]. 金属学报, 2015, 51(12): 1441-1448.

WANG Bing-shu, DENG Li-ping, CHAPUIS A, GUO Ning, LI Qiang. Study of twinning behavior of AZ31 Mg alloy during plane strain compression[J]. Acta Metall Sin, 2015, 51(12): 1441-1448.

[13] OSTAPOVETS A, SERRA A. Slip dislocation and twin nucleation mechanisms in hcp metals[J]. Journal of Materials Science, 2017, 52(1): 533-540.

[14] LECLERCQ L, CAPOLUNGO L, Rodney D. Atomic-scale comparison between twin growth mechanisms in magnesium[J]. Materials Research Letters, 2014, 2(3): 152-159.

[15] XU Hong-lu, SU Xiao-ming, YUAN Guang-yin, JIN Zhao-hui. Primary and secondary modes of deformation twinning in HCP Mg based on atomistic simulations[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(12): 3804-3809.

[16] 刘 筱, 朱必武, 李落星, 唐昌平. 挤压态AZ31镁合金热变形过程中的孪生和织构演变[J]. 中国有色金属学报, 2016, 26(2): 288-295.

LIU Xiao, ZHU Bi-wu, LI Luo-xing, TANG Chang-ping. Twinning and texture evolution in extruded AZ31 magnesium alloy during hot deformation[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(2): 288-295.

[17] 娄 超, 张喜燕, 任 毅. 动态塑性变形下AZ31镁合金的孪生特征[J]. 中国有色金属学报, 2015, 25(10): 2642-2648.

LOU Chao, ZHANG Xi-yan, REN Yi. Twinning characteristic of AZ31 magnesium alloy during dynamic plastic deformation[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2642-2648.

[18] 胡轶嵩, 杨 平, 赵祖德, 马端骋. 利用取向成像研究镁合金的孪生过程[J]. 中国有色金属学报, 2004, 14(1): 105-111.

HU Yi-song, YANG Ping, ZHAO Zu-de, MA Duan-cheng. Investigation of twinning process in magnesium alloy by means of orientation mapping[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(1): 105-111.

[19] KADIRI H E, BARRETT C D, WANG J, TOME C N. Why are 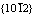twins profuse in magnesium?[J]. Acta Mater, 2015, 85: 354-361.

[20] LI B, ZHANG X Y. Twinning with zero twinning shear[J]. Scripta Mater, 2016, 125:73-79.

[21] LENTZ M, RISSE M, SCHAEFER N, REIMERS W, BEYERLEIN I J. Strength and ductility with 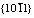- 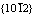double twinning in a magnesium alloy[J]. Nat Commun, 2016, 7: 11068-11074.

[22] 况新亮, 刘天模, 何杰军. 基于镁合金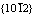孪生的织构调整及屈服行为演变[J]. 中国有色金属学报, 2014, 24(5): 1111-1117.

KUANG Xin-liang, LIU Tian-mo, HE Jie-jun. Evolution of texture and yielding behavior induced by 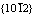twinning of magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(5): 1111-1117.

[23] 娄 超, 张喜燕, 汪润红, 段高林, 刘 庆. 退孪生行为以及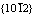孪晶片层结构对镁合金力学性能的影响[J]. 金属学报, 2013, 49(3): 291-296.

LOU Chao, ZHANG Xi-yan, WANG Run-hong, DUAN Gao-lin, LIU Qing. Effects of untwining and 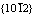twin lamellar structure on the mechanical properties of Mg alloy[J]. Acta Metall Sin, 2013, 49(3): 291-296.

[24] 杨续跃, 张 雷. 镁合金温变形过程中的孪生及孪晶交叉[J]. 金属学报, 2009, 45(11): 1303-1308.

YANG Xu-yue, ZHANG Lei. Twinning and twin intersection in AZ31 Mg alloy during warm deformation[J]. Acta Metall Sin, 2009, 45(11): 1303-1308.

[25] SUN D Y, MENDELEV M I, BECKER C A, KUDIN K, HAXHIMALI T, ASTA M, HOYT J J, KARMA A, SROLOVITZ D J. Crystal-melt interfacial free energies in hcp metals: A molecular dynamics study of Mg[J]. Phys Rev B, 2006, 73(2): 024116.

[26] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19.

[27] STUKOWSKI A. Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool[J]. Modelling Simul Mater Sci Eng, 2010, 18(6): 2154-2162.

[28] TU J, ZHANG S. On the 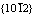twinning growth mechanism in hexagonal close-packed metals[J]. Materials & Design, 2016, 96: 143-149.

[29] LIU B Y, WANG J, LI B, LU L, ZHANG X Y, SHAN Z W, LI J, JIA C L, SUN J, MA E. Twinning-like lattice reorientation without a crystallographic twinning plane[J]. Nat Commun, 2014, 5(2): 3297-3302.

Mobility comparison of twin interfaces between 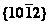 and 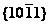 for magnesium alloy

LI Heng¹, LIU Zhao¹, ZHANG Zhen², PENG Jing-hua²

(1. Institute of Industry & Equipment Technology, Hefei University of Technology, Hefei 230009, China;

2. School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract: Deformation twinning is one of the main plastic deformation modes of magnesium alloy. Two main types of twin are 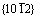 and 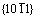. There have great differences between the morphology of two kinds of common twins.  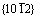tensile twins mostly form in non-basal plane oriented grain. Once the twins have formed, it will expand rapidly, and gradually engulf the matrix. Thus the morphology features of  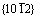twins are mostly lenticular. However,  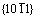compression twins mostly form in basal plane oriented grain. After the formation of these twins, it is difficult to expand laterally, and the morphology features of  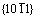twins are mostly narrow-flake. The combination of molecular dynamics method and microstructure experiment observation is used to establish the atomic models of two kinds of twins. In addition, the size and loading mode of the two models are consistent. This paper contrasts the mobility of two kinds of twin interfaces through analysis of stress-strain curve, microstructure and interface migration mode. And the reasons for the difference interface mobility are explained from the point of view of atomic motion and dislocation slip. The simulation and experimental results show that the stress required for 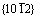twin boundary migration is lower than that for 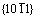twin boundary. The migration of  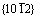twin boundaries presents “bow” shape mode, while  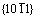twin boundaries migrate with “step” mode. Actually, the migration of 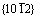twin boundaries is the process of mutual transformation of Basal planes and Prism planes. Interestingly, the atomic arrangements of Basal plane and Prism plane are similar, thus it is easy to implement the mutual conversion process. However, it is found that there are periodic interfacial dislocations on the  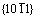twin interface by TEM observation and simulation results, and the interfacial dislocations will hinder the movement of twin interface. It is also found that there are basal plane dislocation spiling up at the interface; it can provide energy for the migration of  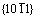twin boundaries. Therefore,  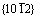twin boundaries are easier to form large-scale and rapid migration than  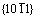twin boundaries.

Key words: magnesium alloy; 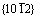 twin; 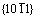 twin; mobility of twin interfaces; molecular dynamics simulation

Foundation item: Projects(51401072, 51605128) supported by the National Natural Science Foundation of China

Received date: 2017-12-21; Accepted date: 2018-07-16

Corresponding author: ZHANG Zhen; Tel: +86-551-62902665; E-mail: turkeyzz@126.com

(编辑  何学锋)

基金项目：国家自然科学基金资助项目(51401072，51605128)

收稿日期：2017-12-21；修订日期：2018-07-16

通信作者：张  真，副教授，博士；电话：0551-62902665；E-mail：turkeyzz@126.com