网络首发时间: 2015-04-07 09:26
稀有金属 2015,39(12),1095-1100 DOI:10.13373/j.cnki.cjrm.2015.12.006
金属钌同素异构体问题的第一性原理计算研究
陈松 陆建生 谢明 潘勇 胡洁琼 王松
摘 要:
针对Ru同素异构问题,先假定Ru可能结构为fcc,hcp,bcc,bct,而后用密度泛函方法计算这些结构的基态能量、晶格常数、弹性系数矩阵等参数。各结构内聚能为hcp<fcc<bcc<bct,与已有计算一致。晶格常数也与计算和实验一致,计算发现密度为hcp>fcc>bcc>bct,比值为:1.000∶0.995∶0.967∶0.873。计算得各结构弹性系数矩阵,用Voigt理论计算得0 K的体弹性模量、杨氏模量、剪切模量、泊松比等参量,结合塑脆判据发现bcc和bct是塑形晶体,hcp和fcc为脆性晶体,对hcp结构的结论与实验一致。基于晶体力学稳定性判据首次发现0 K下只有bcc结构是不稳定的,其他结构稳定。从热力学角度研究结构的稳定性,用德拜准简谐理论及公式,结合力学性能计算数据,计算了常压下各结构的Ru的自由能曲线,分析得到常压下0~2343 K内Ru稳定性是:hcp>fcc>bcc>bct,2343 K至熔点2523 K内Ru稳定性是:hcp>bcc>fcc>bct。比较已有数据和计算结果,可确定常压下在Ru熔点以下只有hcp结构Ru存在,解决了Ru的同素异构问题。
关键词:
钌;同素异构体;密度泛函;稳定性;
中图分类号: TG146.38
作者简介:陈松(1976-),男,浙江龙游人,博士研究生,研究员,研究方向:贵金属材料制备和计算材料学研究;E-mail:cs@ipm.com.cn;;陆建生,教授;电话:0871-68328841;E-mail:fermi_gas@sina.com;
收稿日期:2014-04-20
基金:国家自然科学基金项目(51267007,51461023,U1302272,51164015);云南省自然科学基金项目(2010CD126,2012FB195,2015FA042);云南省省院省校项目(2012IB002);云南省创新团队项目(2012HC027)资助;
First-Principle Investigation on Problem of Ruthenium Allotropic Phase Stability
Chen Song Lu Jiansheng Xie Ming Pan Yong Hu Jieqiong Wang Song
School of Materials Science and Engineering,Kunming University of Science and Technology
Sate Key Laboratory of Advanced Technologies for Comprehensive Utilization of Precious Metals,Kunming Institute of Precious Metals
Abstract:
In order to solve the problem of ruthenium allotropic phase stability,firstly,the possible phase structures of ruthenium were assumed to be fcc,hcp,bcc and bct,and then lattice parameter,ground state energy and elastic coefficient matrix were calculated by density function theory for those phase structures. The calculation results of cohesive energy showed the order of hcp < fcc < bcc< bct,and agreed well with other calculation results. The calculation results of lattice constant were the same with experimental results. The calculation results of density was in the order of hcp > fcc > bcc > bct,and the ratio was 1. 000∶ 0. 995∶ 0. 967∶ 0. 873. The important mechanical parameters under 0 K including elastic constants,bulk modulus,shear modulus and Poisson' s ratio were all based on calculation results of elastic constants matrix by Voigt method. It was first found that only the bcc phase was unstable from phase stability criterion and calculation results at 0 K. Based on Debye-harmonic theory and many formulas,the thermodynamic stable order was hcp > fcc > bcc > bct from 0 to 2343 K,and that from 2343 K to melting point of ruthenium was hcp > bcc > fcc > bct. The hcp structure was the most stable ruthenium structure under normal pressure,and this conclusion agreed with the present thermodynamic calculation results,and the problem of ruthenium allotropic phase stability was solved.
Keyword:
ruthenium; allotropic phase; density function theory; stability;
Received: 2014-04-20
钌( Ru) 是周期表第Ⅷ族中铂族金属中的一种。Ru广泛地应用于化工催化剂、军用电接触材料、高温合金、电容制造、燃料电池、计算机硬盘制造等领域中,在国民经济、电子工业、国防工业等领域发挥着十分重要的作用[1,2,3,4,5]。
耶盖尔和罗津博姆测量了Ru在0 ~ 1600 ℃ 的比热和电阻温度系数,以及0 ~ 1500 ℃的对铂热电动势,根据测量结果认为金属钌具有4种同素异构体: 在1035 ℃时存在 α-Ru( 密排六方) β-Ru转变,在1190 ℃ 时存在 β-Ruγ-Ru转变,在1500 ℃ 时存在 γ-Ruδ-Ru转变,但该研究并未给出除 α-Ru( 相结构如图1) 以外其他相的具体结构的测量数据[1,2]。所以后期也有人进行了热电势测量, 发现一直到1600 ℃ 都没有发现热电势有突变,这与耶盖尔和罗津博姆的测量不符。同时还有人测量了Ru的晶格常数,发现一直到1300 ℃ 都没有发现晶格常数的突变。还有人研究了钌的其他物理性能,一直到1200 ℃ 也未发现突变存在。在这些实验结果的基础上人们认为金属Ru只存在 α- Ru( 密排六方) 而不存在同素异构体[3]。但对于该问题鲜有从理论上对其进行相关研究,同时对于金属Ru可能存在结构的稳定性等关系和数据也未给出相关信息。所以对于金属钌的同素异构体问题需要进一步进行研究。
首先通过分析假定了Ru的同素异构体可能存在的结构,而后采用第一性原理计算方法中的密度泛函理论计算了这些结构的晶格常数、弹性常数等,并从热力学和动力学上对这些结构的稳定性进行判断和比较,最终从理论上解决该问题。
1金属钌可能存在的相结构
假定若Ru的同素异构体存在,其可能存在的相结构可以通过分析元素周期表中与Ru相近邻元素的相结构得以确定。周期表第VII族中第二组( Ru,Rh,Pd) 的性质与第一组( Fe,Co,Ni) 差别较大,而与第三组( Os,Ir,Pt) 的性质接近; 且Ru与Os性质接近但与Fe性质差别较大。通过文献资料可以发现与Ru相邻的Fe,Co,Ni,Rh,Os,Ir, Pt,Mn,Tc,Re,Cr,Mo,W的主要结构有: fcc ( γ-Fe,β-Co,α-Ni,γ-Mn,Rh,Ir,Pt) ,hcp ( α- Co,Os,Tc,Re) ,bcc ( α-Fe,δ-Fe,α-Mn,β-Mn, δ-Mn) 3种结构。α-Ru是hcp结构,而Ru其他的可能结构就在fcc、hcp和bcc中,同时本研究也考虑了简单立方bct结构。
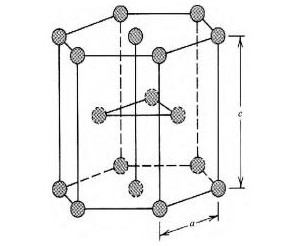
图1密排六方的Ru相结构图( α-Ru) Fig. 1 Close packed hexagonal phase structure of Ru( α-Ru)
2实验
基于量子力学基本原理的第一性原理计算是目前进行相结构和稳定性研究重要方法[6],本研究采用第一性原理计算方法中的密度泛函方法进行计算,主要借助Material Studio软件中的Castep模块进行Ru的同素异构体结构问题的计算工作。 Castep模块中的计算主要是基于Kohn-Sham方程的密度泛函理论,目前该模块计算得到的结果均是材料在0 K下的数值,所以与实验结果进行比较时最好也是0 K下实验结果。
前期的计算实验均发现采用广义梯度近似( GGA) ,Perdew Wang ( 1991) 泛函形式确定交换和相关势,计算结果较接近实际测量值。计算过程主要是: 分别建立hcp( α-Ru) ,fcc,bcc,bct结构的钌晶格; 接着进行几何优化来确定结构能量最低时的晶格参数; 接着在此基础上计算晶格的基态能量,以及弹性模量矩阵、弹性模量等力学参数等。同时为了便于比较计算结果,计算中采用的一些参数基本相同: ( 1) 倒易空间中平面波计算的最大截止能量为340. 0 e V,计算收敛精度1. 0 × 10- 6e V·atom- 1; ( 2) 布里渊区的k矢量选为12 × 12 × 12,自恰迭代次数为100次; ( 3 ) 采用超软赝势; ( 4) 空带为10个,电子总能自恰用Pulay密度混合算法。
3结果与讨论
通过计算得到了不同结构的Ru在0 K下的晶格常数、内聚能、密度、弹性常数等数值,并将这些结果与0 K下实验结果进行了比较。
3. 1不同结构Ru的晶格常数的计算结果
通过几何优化计算得到的晶格常数,在此基础上计算得出相应的密度。通过表1可以发现hcp结构的优化晶格常数均比0 K下的测量结果大,因此计算后的密度比实测密度小,相对误差为1. 61% ,而c / a比值与实验值1. 581吻合。比较不同结构优化计算得到的密度,发现hcp > fcc > bcc > bct,比值为: 1. 000∶ 0. 995∶ 0. 967∶ 0. 873。
表2给出了已有的关于不同结构Ru的晶格常数的计算结果,从表2中可以发现本研究得到的hcp晶格常数比Wang等[7]的计算结果小且更接近实测值,而且其他结构的数值也小于Wang的计算结果。同时本研究给出了以往均未进行计算的bct结构的晶格常数。
3. 2不同结构Ru的内聚能的计算结果
单个Ru原子的计算电子基态为: 4s24p64d75s1, 计算得到的单个Ru原子的基态能量E0=- 2594. 60564 e V·atom- 1。以该能量为基准可以确定不同结构的内聚能,从而可以比较0 K下的不同结构的稳定性和转化能量。
从表3中数据可以发现体系能量为: hcp < fcc < bcc < bct,fcc的能量只是略高于hcp( 1. 246% ) , bcc的能量高于hcp( 7. 192% ) ,而bct的能量高于hcp( 12. 486% ) 。
从表4中的数据可以发现,其他研究者的计算表明体系能量同样为: hcp < fcc < bcc。本研究计算结果只高于参文[7]中的计算结果,但给出了其他研究者未给出的bct结构的能量值。在0 K下相结构稳定的热力学能量G = H - TS( G - 吉布斯自由能,H - 焓,S - 熵,T - 热力学温度) ,而T = 0 K故G = H≈E( E - 内能) ,所以可以从内聚能判断结构的稳定性,从而可以发现稳定性从高到低依次为: hcp > fcc > bcc > bct。
表1不同Ru结构的晶格常数的计算结果Table 1 Calculated lattice constants of different Ru structures 下载原图

表1不同Ru结构的晶格常数的计算结果Table 1 Calculated lattice constants of different Ru structures
表2已有Ru结构的晶格常数结果Table 2 Existing results of Ru lattice constants 下载原图

表2已有Ru结构的晶格常数结果Table 2 Existing results of Ru lattice constants
表3不同Ru结构的能量的计算结果Table 3 Calculated energy of different Ru structures 下载原图
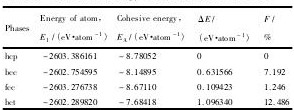
EA=E1-E0;ΔE=E-Ehcp;F=ΔE/Ehcp
表3不同Ru结构的能量的计算结果Table 3 Calculated energy of different Ru structures
表4不同研究者的Ru结构能量计算结果Table 4Ru structure energy calculations by different re- searchers ( e V·atom- 1) 下载原图
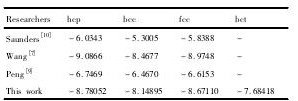
表4不同研究者的Ru结构能量计算结果Table 4Ru structure energy calculations by different re- searchers ( e V·atom- 1)
3. 3不同结构Ru的弹性性能相关参数的计算结果
通过软件计算可直接得到不同结构的弹性系数矩阵Cij,而体弹性模量B,剪切模量G均采用Voigt理论[11]计算得到,而泊松比 ν = ( 3B - 2G) /2 ( G + 3B) ,计算结果列于表5中。表6中给出了本研究和其他研究者的体积模量的计算结果,从表6中可以发现计算得到的hcp结构的体积模量B与实验值接近程度依次为: Peng等[9]、本研究、 Saunders等[10]。所有计算的结果中不同结构的体积模量B从大到小依次为: hcp > fcc > bcc > bct。 从B /G比值可以发现hcp和fcc结构的值均小于1. 75,表现为脆性晶体[12,13],而bcc和bct结构的值均大于1. 75,表现为塑性晶体。实验也已经发现hcp结构的Ru确实是脆性晶体。已有hcp结构的实验报道[12]结果为弹性模量E为485,447 GPa, 剪切模量G为172 GPa,泊松比0. 31,通过与表5中的数据比较,实验和计算结果比较接近。
由于hcp属于六角晶系其弹性系数矩阵Cij满足六角晶系的基本关系[15]: ( 1) 独立弹性常量为C11,C12,C13,C33,C44; ( 2) 独立弹性常量与其他量的关系为C66= ( C11- C12) /2,C44= C55,C11= C22,C12= C21,C13= C31。六角晶系相结构的力学稳定性的判别标准为: ( C11+ 2C12) C33- 2C213> 0, C11- C12> 0,C11> 0,C33> 0,C44> 0。通过计算后发现该结构从力学上是可以稳定存在的。并且在平行hcp的密排面上杨氏模量、泊松比等是各向同性的, 而在垂直hcp的密排面的方向上才表现出异性的。
由于fcc,bcc,bct均属于立方晶系其弹性系数矩阵Cij满足立方晶系的基本关系: ( 1) 独立弹性常量为C11,C12,C44; ( 2) 独立弹性常量与其他量的关系为C11= C22= C33,C12= C21= C13= C31=C23=C32,C44=C55=C66。
立方晶系相结构的力学稳定性的判别标准[15]为: C11> 0,C12> 0,C44> 0,C11- C12> 0,C11+ 2C12> 0。通过计算后发现fcc,bct从力学上是可以稳定存在的,并且杨氏模量、泊松比等是各向同性的。但是通过计算后发现bcc结构不满足C11- C12> 0,所以该结构在0 K下从力学上是不稳定的。
3. 4分析和讨论
通过对以上的计算结果的热力学和力学稳定性分析,可以认为在0 K下Ru的稳定性从高到低依次为: hcp > fcc > bcc > bct。对于常压下高于0 K时这4种结构的热力学稳定性,采用德拜准简谐理论[16,17]进行计算,首先自由能:
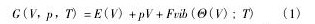
其中Fvib(Θ(V);T)是晶格振动产生的自由能(1mol的原子),其中Θ为德拜温度,V为1 mol物质的体积,p为常压,E(V)是与体积相关的其他能量,即表3中的内聚能EA乘以阿弗加德罗常数NA。
其中

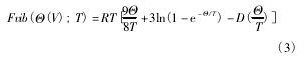
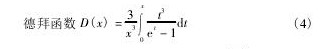
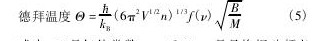
式中,R是气体常数,x = Θ/T,t是晶格振动频率进行无量纲处理后的变量, 是约化普朗克常数。
其中
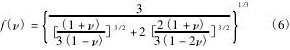
表5不同Ru结构的弹性常数、体积模量、剪切模量和泊松比的计算结果Table 5 Different Ru structure calculation results of elastic constants,bulk modulus,shear modulus and Poisson's ratio 下载原图

表5不同Ru结构的弹性常数、体积模量、剪切模量和泊松比的计算结果Table 5 Different Ru structure calculation results of elastic constants,bulk modulus,shear modulus and Poisson's ratio
表6不同研究者的Ru结构体积模量计算结果Table 6Bulk modulus ( B) calculations of different Ru structures by different researchers( GPa) 下载原图
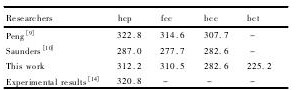
表6不同研究者的Ru结构体积模量计算结果Table 6Bulk modulus ( B) calculations of different Ru structures by different researchers( GPa)
式中,n为每个原胞中包含的原子数,kB为玻尔兹曼常数,M为每个原胞中分子的摩尔质量,B为体弹性模量,ν 为泊松比。
实验测得的hcp的德拜温度为600 K[7]。本研究计算得到hcp,fcc,bcc,bct的德拜温度分别为557. 1,546. 7,231. 1,182. 0 K。目前只有Peng等[9]采用OA理论计算得到hcp,fcc的德拜温度分别为600. 0,594. 0 K。
主要基于表3和表5中的数据和公式( 1) ~ ( 6) 计算了各结构的自由能,其中压力为一个大气压即p0= 0. 101325 MPa。
图2中给出了0 ~ 3000 K自由能计算结果,从图2中可以发现,随着温度的升高4个结构的自由能均下降。当温度小于2343 K时各结构自由能从高到低依次为: bct > bcc > fcc > hcp,当温度在2343 ~ 2774 K之间时各结构自由能从高到低依次为: bct > fcc > bcc > hcp,当温度在2774 ~ 3000 K之间时各结构自由能从高到低依次为: bct > fcc > hcp > bcc。为了便于分析,图3给出了其他结构与hcp结构自由能的差值曲线。图4给出了取自文献[18]的bcc,fcc,液相结构与hcp结构自由能的差值曲线。
通过比较图3和4可以发现。本研究给出的fcc转变为hcp的温度为22936 K,而SGTE( Scien- tific Group Thermodate Europe ) 给出的是5208 K。 bcc转变为fcc的温度为2343 K,而SGTE给出的是3397 K。bcc转变为hcp的温度为2774 K,而SGTE给出的是4257 K。bct转变为hcp相变温度为3807 K,SGTE给出的hcp的熔化温度为2607 K[18],而文献给出的实测值是2523 K[19]。同时从本研究和SGTE的数据,均可发现随着高温升高bcc结构自由能下降速度大于其他3种结构,所以与其他结构的自由能曲线均有交叉。同时基于以上分析可以得出常压下在Ru熔点以下只有hcp结构的Ru最稳定,不存在其他结构,从而解决了Ru的同素异构体问题。同时对于Ru基硼化物的研究也具有重要参考价值[20]。
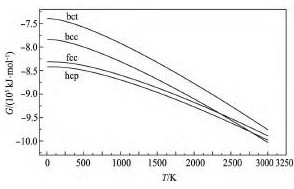
图2不同结构Ru的自由能温度曲线Fig. 2 Gibbs energy curves of different Ru structures
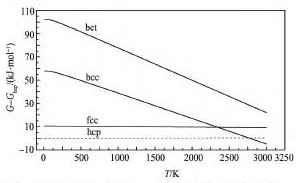
图3不同结构Ru相对于hcp结构的自由能温度曲线Fig. 3Gibbs energy curves of different Ru structures relative to hcp structure
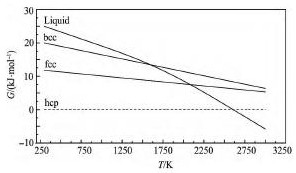
图4不同结构Ru相对于hcp结构的自由能温度曲线( SGTE) Fig. 4Gibbs energy curves of different Ru structures relative to hcp structure( SGTE)
4结论
针对Ru的同素异构体问题。通过分析Ru假定的可能结构为fcc,hcp,bcc,bct。并用密度泛函方法计算这些结构的基态能量、晶格常数、弹性系数矩阵、自由能等参数计算研究。通过分析和比较相应结果,得到以下结论:
1. 0 K下各体系能量大小为hcp < fcc < bcc < bct,密度大小为hcp > fcc > bcc > bct,比值为: 1. 000∶ 0. 995 ∶ 0. 967 ∶ 0. 873,hcp和fcc为脆性晶体,bcc和bct是塑性晶体。
2. 从结构的力学稳定判据分析,发现0 K下只有bcc结构在力学上是不稳定的。
3. 基于德拜准简谐理论得到0 ~ 2343 K温度范围内Ru稳定性从高到低是: hcp > fcc > bcc > bct,而在2343 K至Ru的熔点2523 K温度范围内,Ru稳定性从高到低是: hcp > bcc > fcc > bct。
4. 常压下在Ru熔点以下只有hcp结构的Ru存在,解决了Ru的同素异构体问题。
参考文献
[1] Lavenskii M I.Physical and Chemical Property of Elements(Vol.2)[M].Beijing:Industry Press,1965.260.(斯拉文斯基.元素的物理化学性质(下册)[M].北京:工业出版社,1965.260.)
[2] Xue S L,Ma H,Liu Z Y.Inorganic Chemistry Series:Platinum Group(Vol.9)[M].Beijing:Science Press,1996.404.(徐绍龄,马衡,刘振义.无机化学丛书(第九卷):铂系[M].北京:科学出版社,1996.404.)
[3] Tang Q L,Qu Z H.Platinum Group Metals[M].Beijing:Metallurgy Industry Press,1990.316.(谭庆麟,阙振寰.铂族金属[M].北京:冶金工业出版社,1990.316.)
[4] Luo J F,Ding Z C,Dong T Y,He J J,Wang X P,Jiang X.Study of manufacture process on Ru sputtering target by PM[J].Powder Metallurgy Industry,2012,22(1):28.(罗俊锋,丁照崇,董亭义,何金江,王欣平,江轩.钌金属溅射靶材烧结工艺研究[J].粉末冶金工业,2012,22(1):28.)
[5] Liu S J.An unusual potential resource of platinum group metals-“fission platinoids(FPs)”from nuclear waste materials[J].Precious Metals,2013,34(4):60.(刘时杰.一种特殊的铂族金属潜在资源-核废料中的“裂变假铂-FPs”[J].贵金属,2013,34(4):60.)
[6] Zhang W,Chen W Z,Jiang Z Y.First-principles study of lattice dynamic of Ir Ti alloy[J].Acta Physica Sinica,2012,61(14):148105.
[7] Wang Y,Curtarolo S,Jiang C,Arroyave R,Wang T,Ceder G,Chen L Q.Ab initio lattice stability in comparison with CALPHAD lattice stability[J].CALPHAD,2004,28(1):79.
[8] John W A.Crystallographic properties ruthenium[J].Platinum Metals Rev.,2013,57(2):127.
[9] Peng H J,Zhou J L,Xie Y Q.Thermodynamic properties and heat capacity of Ru metal in HCP,FCC,BCC and liquid state[J].Nonferrous Met.Soc.China,2010,20:1950.
[10] Saunders N,Miodowik A P,Dinsdale A T.Metastable lattice stabilities for the elements[J].CALPHAD,1988,12(4):351.
[11] Hill R.The elastic behaviour of a crystalline aggregate[J].Proceedings of the Physical Society.Section A.1952,65(5):349.
[12] Pugh S P.Relation between the elastic moduli and the plastic properties of polycrystalline pure metals[J].Philosophical Magazine,1954,45(367):823.
[13] Chen K,Zhaoa L R,Tse J S.Elastic properties of platinum Rh and Rh3X compounds[J].Physics Letters A,2004,331(6):400.
[14] Savitskii E M.Handbook of Precious Metals[M].New York:Hemisphere Publishing Corporation,1989.126.
[15] Born M,Huang K.Dynamical Theory of Crystal Lattices[M].Oxford:Clarendon Press,1954.141.
[16] Wang Z X.Introduction to Statistical Physics[M].Beijing:People Knowledge Press,1965.271.(王竹溪.统计物理学导论[M].北京:人民知识出版社,1965.271.)
[17] Otero A,David A P,Victor L.GIBBS2:a new version of the quasiharmonic model code II.Models for solid-state thermodynamics,features and implementation[J].Computer Physics Communications,2011,182(10):2232.
[18] Dinsdale A T.SGTE data for pure elements[J].CALPHAD,1991,15(4):317.
[19] Ye D L.Handbook of Practical Inorganic Thermodynamic Dates[M].Beijing:Metallurgy Industry,2002.860.(叶大伦.实用无机物热力学数据手册[M].北京:冶金工业出版社,2002.860.)
[20] Liu H J,Pan Y,Guan W M,Zhang K H,Yin C P,Du Y L.Research progress in superhard transition metal borides[J].Chinese Journal of Rare Metals,2013,37(4):633.(刘洪江,潘勇,管伟明,张昆华,殷聪朋,杜怡霖.过渡金属硼化物超硬材料的研究进展[J].稀有金属,2013,37(4):633.)