文章编号：1004-0609(2013)05-1295-06

新型亚稳β钛合金Ti2448的温变形行为及本构模型

王哲君，强洪夫，王学仁

(西安高新技术研究所 601室，西安 710025)

摘  要：采用压缩实验研究应变速率和变形温度对新型亚稳β钛合金Ti2448温变形行为的影响。热模拟压缩实验在Gleeble-3800热模拟机上进行，变形温度为473~673 K，应变速率为0.001~10 s^-1，变形程度为45%。结果表明：在高、低应变速率下合金呈现不同的变形特性。低应变速率(0.001~0.1 s^-1)下，流动曲线呈现明显的应变硬化特性；在10 s^-1的高应变速率下，流动应力在达到饱和后，因温升效应而下降；在673 K变形温度下流动应力因材料内部相变而具有显著的应变速率负敏感性。基于分段外推饱和模型和改进的Voce 模型分别构建Ti2448合金在温变形高、低应变速率下的流动应力模型；该模型得到的预测曲线(应力—应变曲线)和实验曲线吻合较好，能够有效预测Ti2448合金在温变形过程中的流动应力，其中，改进的Voce模型能同时较好地描述饱和型和非饱和型应变硬化特性。

关键词：亚稳β钛合金；温变形；本构模型

中图分类号：TG146.2           　   　     文献标志码：A

Warm deformation behavior of new kind of metastable β titanium alloy Ti2448 and its constitute model

WANG Zhe-jun, QIANG Hong-fu, WANG Xue-ren

(601 Staff Room, Xi’an High Technology Institute, Xi’an 710025, China)

Abstract: The effects of strain rate and deformation temperature on warm deformation behavior of a new kind of metastable β titanium alloy Ti2448 were investigated by using compression tests. The experiments were carried out on a Gleeble-3800 thermo-mechanical simulator at deformation temperatures of 473-673 K, strain rates of 0.001-10 s^-1, and height direction reduction of 45%. The results show that there are different deformation behaviors at high and low strain rates. At low strain rates (0.001-0.1 s^-1), there are obvious work hardening behaviors in flow stress curves. At the high strain rate of 10 s^-1, the alloy presents obvious hardening firstly, then saturated state and further softening caused by temperature rise finally. At 673 K, the alloy significantly exhibits the stain rate negative sensitivity because of the phase change. Based on the model in which the whole stress—strain curve is divided into the strain hardening part and the saturated state part and the modified Voce model, constitutive models were developed to describe the flow behaviors of Ti2448 alloy at high and low strain rates, respectively. The stress—strain curves predicted by the developed model well fit with the experimental results, which confirms that the developed model can predict the flow stress of Ti2448 alloy validly and the modified Voce model can describe the strain hardening behavior of both the saturated state and the unsaturated state.

Key words: metastable β titanium alloy; warm deformation; constitutive model

亚稳β钛合金具有比强度高、冷热成型性、深淬透性优异及抗腐蚀性良好等优点，因此，在过去几十年里，该类钛合金的重要性逐步提高，在许多国家得到越来越多的关注^[1]。在实际工程应用中，只有全面了解所使用材料在很宽变形温度、较大应变速率范围等条件下的性能，才能充分开发和有效利用其潜力。

目前，许多材料研究者对亚稳β钛合金在热处理等条件下的显微组织与性能、热变形特性等开展了相应的研究^[2-4]，然而，关于该类合金温变形特性及本构模型的研究不多。因此，研究亚稳β钛合金在温变形条件下的变形特性及构建相应的本构模型对亚稳β钛合金的工程应用具有重要意义。

本文作者在新型亚稳β钛合金Ti2448轴向温压缩实验的基础上，分析温变形过程中应变、应变速率和变形温度对流动应力的影响及材料的流动应力曲线特征，并建立有效描述其温变形特性的本构模型，最终通过与实验曲线比较来检验模型的有效性。

1  实验

实验用Ti2448钛合金试样是从板材上沿厚度方向截取的表面打磨光滑后的尺寸为d8 mm×12 mm的圆柱体。温压缩实验在Gleeble-3800热模拟机上进行，变形温度为473~673 K，应变速率分别为0.001、0.1和10 s^-1，所有试样沿板材厚度方向的轴向压缩量为45%，试样在压缩前保温5 min。

2  变形行为分析

2.1  流动应力曲线特征

图1所示为Ti2448钛合金在不同温度和应变速率下温变形时的流动应力曲线。由图1可以得出：1) 变形温度和应变速率影响流动应力，但流动应力随变形温度和应变速率变化的规律与热变形时不同，即流动应力不随应变速率的升高或变形温度的下降而一直增大。其中，在塑性变形初期和673 K变形条件下尤为明显，流动应力随应变的增加逐渐呈现出应变速率的负敏感性，即流动应力随应变速率的增加而降低。2) 变形初期流动应力增加很快，几乎呈直线上升。3) 随变形量的增大，变形温度和应变速率对流动应力的影响越来越明显。4) 在不同应变速率和变形温度条件下，Ti2448合金的流动曲线表现为不同的特征。在低应变速率范围内(0.001~0.1 s^-1)，流动应力随应变的增加持续增大，流动曲线呈现出明显的应变硬化特征；而在高应变速率范围内(10 s^-1)，随应变的增加，流动应力首先达到饱和，随后逐渐下降。同时，流动应力达到饱和所需的变形量与变形温度相关，随变形温度的升高而减小。5) 高应变速率变形条件下流动应力曲线呈现明显的锯齿状波动。

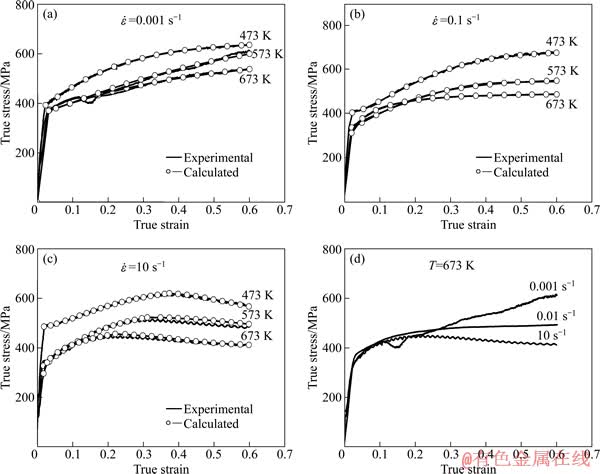
图1  Ti2448钛合金在不同温度和应变速率下的流动应力曲线

Fig. 1  Flow stress curves for Ti2448 alloy at different temperatures and strain rates

2.2  变形特性分析

1) 流动应力曲线在673 K变形条件下呈现的应变速率负敏感性与材料内部微观组织变化有关。在此变形温度条件下，低应变速率有利于材料在慢速变形过程中发生相变，导致应力水平持续上升，使变形进入α+β两相区间^[5]。2) 变形初期流动应力增加较快，这是由于应变速率从0开始，一直增大到实验所采用的值，同时合金变形的硬化速率高于软化速率^[6]。3) 随着变形量的增加，变形温度和应变速率对流动应力的影响逐渐增强，这是由于随着变形量的增大，材料内部一些变形机制开始发生，进而影响材料的宏观力学性能^[7]。4) 应力—应变曲线中发生流动应力的下降，必定是材料内部发生了软化机制。影响材料变形的软化机制主要是动态回复、再结晶和温升效应^[8]，由各软化机制的机理和特性可知，Ti2448合金在高应变速率下变形时，饱和流动应力的出现可能是材料内部动态回复和应变硬化达到动态平衡的结果。同时，动态回复一般不能完全消除材料变形时内部产生的位错，要使流动应力在饱和值之后继续下降，必有其他软化机制的出现^[9]。而温变形的温度较低，一般不易在材料内部发生再结晶^[10]。塑性变形时，随变形量的增大，在较高应变速率、较低变形温度下易发生温升效应，导致流动应力下降^[11]。因此，Ti2448合金在高应变速率下，较大应变处流动应力的下降应是温升效应引起的。5) 饱和应变的出现是软硬化作用达到动态平衡的结果，而变形温度越高，越有利于材料内部软化机制的进行，因此，Ti2448合金变形时，在较高的变形温度下具有较小的饱和应变。6) 高应变速率下，流动曲线呈现的锯齿状波动是材料内部软硬化交互作用的结果^[12]。

可见，Ti2448合金在高、低应变速率下呈现出不同的变形特性。田宇兴等^[13]对Ti2448合金在热变形条件下变形特性的研究同样表明，当合金在高、低应变速率下呈现不同变形特性时，应分不同的应变速率构建其本构模型。因此，本文作者在构建描述Ti2448温变形的本构模型时，分高、低应变速率进行。

3  流动应力模型

3.1  低应变速率下的本构模型

由前文分析可知，Ti2448合金在低应变速率下呈现应变硬化特性。自20世纪初起，人们对多晶材料的应变硬化型流变行为进行了大量研究，建立了一些经验或半经验模型。其中，李宏烨等^[14]的研究表明，Voce模型在描述应变硬化流动曲线时具有最好的逼近度，Voce模型的表达式为^[15]

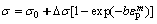                    (1)

式中：Δσ=σ_s-σ₀，σ₀和σ_s分别为屈服应力和饱和流动应力；b和m为材料参数；ε_p为塑性应变。由Voce模型的计算公式可知，要得到应力—应变关系式，必须确定饱和流动应力σ_s，因此，基本的Voce模型是一种描述饱和型应变硬化特性的本构模型。可对于非饱和型应变硬化流动曲线(图1(a)中573~673 K变形条件下流动曲线所示)，无法直接从流动曲线上得出σ_s，只有峰值应力σ_p，而直接采用峰值应力进行计算会存在误差。为使式(1)能在更广泛的范围内描述材料的变形，本文作者将Δσ定义为材料参数，不再受限于饱和流动应力的关系式。为描述变形温度和应变速率对变形的影响，依据LI等^[16]的研究，将屈服应力σ₀、Δσ、b和m均定义为随变形温度和应变速率变化的参数，则可得：

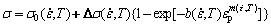   (2)

3.2  高应变速率下的本构模型

当材料变形过程中具有饱和流动特性时，ZHOU等^[17]提出了一种分段式饱和外推模型(见图2)，即将流动曲线看成稳态变形前的应变强化区域(0＜ε＜ε_s)和较大应变处的稳态过程(ε_s≤ε)：

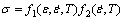                         (3)

式中：f₁描述应变强化区域的变形；f₂描述较大应变处的稳态变形。该模型要满足的边界条件为

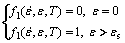                        (4)

式中：ε_s为饱和应变。

式(3)中f₂多采用Arrhenius模型来描述饱和流动应力σ_s或峰值流动应力σ_p。对于变形至稳态的应变强化阶段，表达式较多，其中应用最广泛的是Voce模  型^[18]，即式(1)。综上可得Ti2448合金在高应变速率下的本构模型为

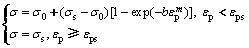      (5)

式中：ε_ps为饱和应变ε_s所对应的饱和塑性应变。由图1(c)及前文分析可知：合金在10 s^-1条件下变形时，流动应力在达到饱和值之后，由于温升效应发生下降。如图2所示，Δσ为因温升效应导致的流动应力的下降值。材料虽然在饱和流动应力前也存在温升效应，但由于应变较小，流动应力的下降较小，因此为有效描述本实验合金的变形，需对饱和值之后的流动应力用式(6)进行修正，即对式(5)塑性应变ε_p≥ε_ps条件下的流动应力进行修正^[19]：

       (6)

式中：η为热转化效率；β为压缩过程的绝热系数，可近似认为只与应变速率有关，根据OH等^[20]的研究，在此选取η=0.9，β=1；Ti2448合金的密度ρ和定压比热容c_p分别为5.42 g/cm³和496 J/(kg·℃)；T₀为等温恒应变速率压缩过程的名义温度；ΔT为因温升效应导致的材料变形温度的升高值；Δσ为因温升效应导致的流动应力的下降值。

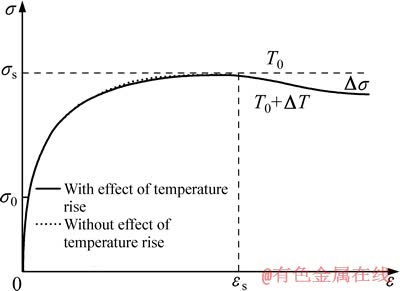
图2  含温升效应的流动应力曲线示意图

Fig. 2  Schematic illustration of flow stress curve showing effect of temperature rise

3.3  确定模型中的参数

屈服应力可以直接从流动曲线上获得，当流动曲线无明显的屈服点时，取2%残余应变对应的点为屈服点。当屈服应力确定之后，要完整地构建本构方程，必须确定模型中其余相关参数的值。将模型计算得到的预测值与实验值的差值平方作为目标函数，用Levenberg-Marquardt最优化方法确定^[21]，即：

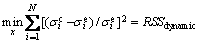             (7)

式中：x代表要确定的参数；N为用于计算的数据总数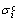；和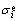分别表示利用模型计算得到的预测值和实验值；RSS代表目标函数的最小值；下标dynamic表示与变形温度和应变速率相关。

3.3.1  低应变速率下参数的确定

由图1可知，该变形条件下的屈服应力随变形温度和应变速率变化的关系较为复杂，不呈单调变化，因此本文作者提出下述多项式表达式：

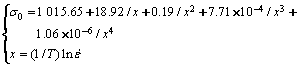    (8)

ZHOU等^[22]指出，参数随变形温度和应变速率的变化关系呈单调关系时，可以采用式(9)所示指数模型表达式进行描述：

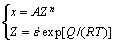                          (9)

式中：x为随变形温度和应变速率变化的参数；A和n为常数；Z为温度补偿应变速率因子；Q在高温下为热激活能(J/mol)；R为摩尔气体常数(8.31 J/(mol·K))；T为变形温度(K)。但在实际计算过程中，经常会遇到虽然参数随变形温度和应变速率的变化关系满足单调规律，但用式(9)并不能很好地描述这种变化。本文作者基于描述流动应力随变形温度和应变速率变化的Arrhenius方程^[23]，提出下述描述参数变化的表达式：

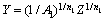                        (10a)

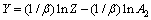                   (10b)

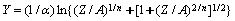     (10c)

式中：Y为随变形温度和应变速率变化的模型参数；A₁、A₂、A、β、α、n₁和n为材料常数；Q在变形温度较低时只表示为材料常数。式(10)中具体表达式的选取，依参数随变形温度和应变速率的变化关系而定。图3所示分别为Δσ、b、ln m与1/T的关系。由图3可知，Δσ、b及ln m与变形温度的倒数1/T符合较好的线性关系，因此，Δσ、b和ln m的表达式可分别采用式(10b)和(10a)来构建，具体形式如下：

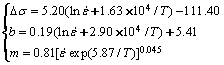        (11)

3.3.2  高应变速率下参数的确定

由于变形发生在同一应变速率下，因此，模型中的参数仅是变形温度的函数，屈服应力σ₀、饱和应力σ_s、参数b、m和塑性饱和应变ε_ps的表达式为

       (12)

4  模型的验证

利用Ti2448合金在不同变形条件下的流动应力数据对所建模型进行验证。所建立的流动应力模型的计算结果与实验数据的对比情况如图1所示。由图1可以看出，利用上述方法确定流动应力曲线能够达到满意的拟合精度。误差分析结果表明，流动应力模型的计算值与实验数据的平均相对误差为3.2%，最大相对误差为7.08%。因此，本文作者所建立的 Ti2448合金流动应力模型能够较好地描述Ti2448合金在温变形过程中的流变行为。

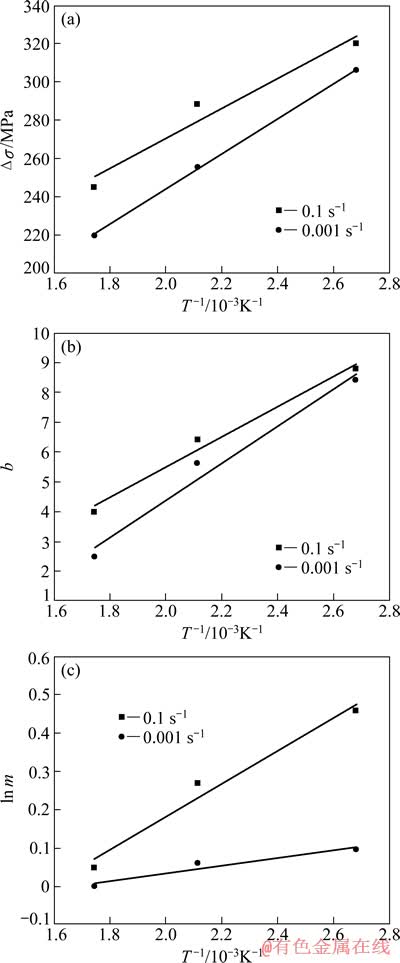
图3  改进Voce模型中参数Δσ、b、ln m与1/T的关系

Fig. 3  Relationship between Δσ (a), b (b) and ln m (c) and 1/T in modified Voce model

5  结论

1) 以Ti2448合金的温变形轴向压缩实验结果为基础，获得了变形温度、应变、应变速率等对流动应力的影响规律。其中，变形温度和应变速率对流动应力均有影响，且随变形量的增大其影响逐渐增强。在高、低应变速率下合金呈现不同的变形特性。低应变速率下，流动曲线呈现明显的应变硬化特性；高应变速率下，流动应力在达到饱和后，因温升效应而下降；在673 K变形温度下流动应力因材料内部相变而具有显著的应变速率负敏感性。

2) 基于分段外推饱和模型和改进的Voce 模型分别构建了Ti2448合金在温变形高、低应变速率下的流动应力模型，并基于Arrhenius方程扩展了参数随变形温度和应变速率变化的表达式形式。采用该模型得到的预测曲线和实验曲线吻合较好，平均相对误差小于5%，能够有效预测Ti2448合金在温变形过程中的流动应力。其中，改进的Voce模型能同时较好地描述饱和型和非饱和型应变硬化特性。

致谢：衷心感谢中国科学院金属研究所沈阳材料科学国家(联合)实验室的郝玉琳研究员、田宇兴博士在完成本实验方面给予的大力帮助。

REFERENCES

[1] 王 震, 洪 权, 赵永庆. 钛合金热变形行为研究[J]. 钛工业进展, 2010, 27(3): 1033-1043.

WANG Zhen, HONG Quan, ZHAO Yong-qing. Hot deformation behavior of titanium alloy[J]. Titanium Industry Processing, 2010, 27(3): 1033-1043.

[2] ZENG L Y, GE P, MAO X N, ZHAO Y Q, ZHOU L. Hot compression behavior of one kind of metastable β titanium alloy[J]. International Journal of Modern Physics B, 2009, 6/7: 777-782.

[3] CUI W F, GUO A H, ZHOU L, LIU C M. Crystal orientation dependence of Young’s modulus in Ti-Nb-based β-titanium alloy[J]. Science China, 2010, 53(6): 1513-1519.

[4] LI S J, CUI T C, HAO Y L, YANG R. Fatigue properties of a metastable β-type titanium alloy with reversible phase transformation[J]. Acta Biomaterialia, 2008, 4: 305-317.

[5] LI Y G, WEI Q G, MA C L, ZHENG L J, LI H X, GE P, ZHAO Y Q. Phase transformation in a β-Ti alloy with good balance between high strength and high fracture toughness[J]. Chinese Journal of Aeronautics, 2009, 22: 535-539.

[6] 俞汉清, 陈金德. 金属塑性成形原理[M]. 北京: 机械工业出版社, 1999: 24.

YU Han-qing, CHEN Jin-de. Engineering plasticity theory and application to metal forming processes[M]. Beijing: China Machine Press, 1999: 24.

[7] ZONG Y Y, SHAN D B, XU M, Y. Flow softening and microstructural evolution of TC11 titanium alloy during hot deformation[J]. Journal of Materials Processing Technology, 2009, 209: 1988-1994.

[8] SENUMA T, YADA H: Annealing processes—Recovery, recrystallization and grain growth[C]//Proceedings of the 7th Ris φ International Symposium on Metallurgy and Materials Science. Roskilde, 1986: 547-552.

[9] NES E, MARTHINSEN K, BRECHET Y. On the mechanisms of dynamic recovery[J]. Scripta Materialia, 2002, 47: 607-611.

[10] MCQUEEN H J. Development of dynamic recrystallization theory[J]. Materials Science and Engineering A, 2004, 387/389: 203-208.

[11] LEE W S, LIN M T. The effects of strain rate and temperature on the compressive deformation behaviour of Ti-6A1-4V alloy[J]. Journal of Materials Processing Technology, 1997, 71: 235-246.

[12] FANG C, ZHANG J, LIAO A L, XUE S Z, YUAN F Q, PAN F S. Hot compression deformation characteristics of Mg-Mn alloys[J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 1841-1845.

[13] 田宇兴, 李述军, 郝玉林. Ti2448合金在不同应变率下的高温变形机制[J]. 中国有色金属学报, 2010, 20(1): 83-86.

TIAN Yu-xing, LI Shu-jun, HAO Yu-lin. Elevated temperature deformation mechanism of Ti2448 alloy at different strain rates[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(1): 83-86.

[14] 李宏烨, 庄新村, 赵 震. 材料常用流动应力模型研究[J]. 模具技术, 2009(5): 1-4.

LI Hong-ye, ZHUANG Xin-cun, ZHAO Zhen. The research on the widely used material flow stress model[J]. Die and Mould Technology, 2009(5): 1-4.

[15] DZIALLACH S, BLECK W, BLUMBACH M. Sheet metal testing and flow curve determination under multiaxial conditions[J]. Advanced Engineering Material, 2007, 9(11): 987-994.

[16] LI X S, WU L Z, CHEN J, ZHANG H B. New approach for modeling flow stress of aluminum alloy 6A10 considering temperature variation[J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 1482-1487.

[17] ZHOU M，CLODE M P. Constitutive equations for modelling flow softening due to dynamic recovery and heat generation during plastic deformation[J]. Mechanics of Materials, 1998, 27: 63-76.

[18] VOCE E. The relationship between stress and strain for homogeneous deformation[J]. Journal of Institute of Metals, 1948, 74: 537-562.

[19] ARSEENAULT R J, BEELER J R, ESTERLING Jr D M. Computer simulation in materials science[C]//Proceedings of ASM Material Science Seminar. Florida: CASM International, 1998: 291-342.

[20] OH S I, SEMIATIN S L, JONAS J. An analysis of the isothermal hot compress test[J]. Metallurgical Transactions A, 1992, 23(3): 963-975.

[21] MILANI A S, DABBOUSSI W, NEMES J A, ABEYARATNE R C. An improved multi-objective identification of Johnson-Cook material parameters[J]. International Journal of Impact Engineering, 2009, 36: 294-302.

[22] ZHOU M, CLODE M P. Hot torsion tests to model the deformation behavior of aluminium alloys at hot working temperatures[J]. Journal of Materials Processing Technology, 1997, 72: 78-85.

[23] SELLARS C M. On the mechanism of hot deformation[J]. Acta Metall, 1966, 14: 1136-1138.

(编辑  陈卫萍)

收稿日期：2012-01-20；修订日期：2013-03-20

通信作者：强洪夫，教授；电话：029-84743700；E-mail：qiulongzaitian@126.com