J. Cent. South Univ. Technol. (2011) 18: 1493-1501

DOI: 10.1007/s11771-011-0865-5

Synthesis of fractal geometry and CAGD models for multi-scale topography modelling of functional surfaces

WANG Qing-hui(王清辉), LI Jing-rong(李静蓉), CHEN Yan-zheng(陈彦政),

PAN Min-qiang(潘敏强), TANG Yong(汤勇)

School of Mechanical and Automotive Engineering, South China University of Technology,Guangzhou 510641, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: In order to support the functional design and simulation and the final fabrication processes for functional surfaces, it is necessary to obtain a multi-scale modelling approach representing both macro geometry and micro details of the surface in one unified model. Based on the fractal geometry theory, a synthesized model is proposed by mathematically combining Weierstrass- Mandelbrot fractal function in micro space and freeform CAGD model in macro space. Key issues of the synthesis, such as algorithms for fractal interpolation of freeform profiles, and visualization optimization for fractal details, are addressed. A prototype of the integration solution is developed based on the platform of AutoCAD’s Object ARX, and a few multi-scale modelling examples are used as case studies. With the consistent mathematic model, multi-scale surface geometries can be represented precisely. Moreover, the visualization result of the functional surfaces shows that the visualization optimization strategies developed are efficient.

Key words: surface roughness; microtopography; fractal geometry; functional surface

1 Introduction

Traditional machining processes are applied to produce finishing surfaces with high precision in both sizes and shapes. However, the fabrication of functional surfaces is expected to produce rough features over machined surfaces with specific morphology so as to facilitate desired functional behaviors of the product, such as improved thermal and mass transfer rate [1-3], biological compliance [4], or enhanced chemical reaction performance [5]. More specifically, for an example in biomedical engineering fields, implant surfaces can be designed with specific microtopography to ensure the biocompatibility of the prosthesis with biological tissues, so that implant-bone fixation can take place through osseointegration, and at the same time, some primitive functionalities of biological structure can be restored [6]. Several investigations revealed that the phenomena like implant-bone fixation, and the resultant strength of healed bone, depend upon the original surface microstructure of the implant [7-8]. Another industrial example is that functional surfaces may have very positive impact on the performance of chemical reaction because of the influence from their surface microstructures on laminar flow with micro-channels [9].

Over the past decades, a number of research efforts were focused on the fabrication of functional surfaces. Experimental studies were conducted to investigate the associated functional properties. Functional design, performance simulation, optimization, and effective control over surface microtopography show significance in improving the equipment performance. The relationship between the functional property of a surface and its micro topographical distribution was investigated for many scientific and engineering applications. Therefore, it is necessary to study a structured model for surface morphology information. With this model, relevant features could be identified and subjected to preferential and customized analysis processes. Hence, a better understanding can be obtained on how the morphology and structure of a surface affect its functional properties. Moreover, instead of individual or local geometry details, the overall topographic distribution of surface is the main impact factor to its functional properties. Therefore, the technology of controlling geometric features at microscopic scale fits in particular with high-precision engineering design and manufacturing applications. As a matter of fact, by manipulation of manufacturing processes parameters, it is possible to effectively control overall microtopography for machined surfaces, which gives strong implications on surface modelling at microscopic levels.

For many conventional manufacturing applications, the design process provides full specification for macro shape of a surface with an additional generic roughness specification to describe surface microtopography. Due to the intrinsic characteristic of functional structures, more specifically, the multi-scale geometric size and the natural surface morphology with non-integral dimension, conventional CAD modelling technologies cannot be directly adopted for design and simulation of functional surfaces. In most cases, the design and simulation of a functional surface require both complete definition of the overall shape of the surface and the full specification of its topography at microscopic scale. In this regards, the design of surface topography needs mathematic modelling and identification of optimal values for design parameters by considering their relationship with functional performance of the surface.

In this work, in order to precisely model functional surfaces at different size scales, i.e. at surface shape macro scale and at micro scale, based on the self-affined fractal features with machined metal surface [10], a general mathematic method is proposed for synthesis of Weierstrass-Mandelbrot (W-M) fractal representation and parametric surface in 3D space. Then, the rough topography with functional surfaces in micro space can be well integrated with freeform solid CAD models in macro space, so that the multi-scale representation of functional surface structures can be established. Some key issues for the synthesis, such as algorithms for fractal interpolation of freeform profiles, and visualization optimization for fractal details, are discussed. A prototype of the proposed approach is developed based on the computer aided geometry design (CAGD) platform of AutoCAD’s Object ARX. The effectiveness of the prototype is demonstrated by multi-scale modelling of wick structures of inner surfaces of a heat pipe.

2 Issues with functional surface modelling

From the size point of view, the structures on the top of machined surfaces come with a large range of variety, which can be generally considered as macro structures (with the size scale of above 1 mm), substructures (with the size scale around 0.1 mm), and microstructures (with the size scale around 0.01 mm or less). In many engineering applications, structures with different scales are used together so that desired functional properties can be achieved. Such structures are the so-called multi-scale functional structures.

From the manufacturing point of view, the functional structures on machined surfaces are usually the results of their manufacturing processes and hence they are controllable. Common manufacturing processes used for surface generation are not likely to have direct full control over surface topography at microscopic scale. These sub-structures are normally formed as derived objects together with macro structures by non- constrained machining conditions. The microstructures appear to be of rough morphology that is distributed randomly over the surfaces of their parent macro- and sub-structures. The distribution of such microstructures follows certain rules in micro space. Figure 1 shows an example of multi-scale structure over a functional surface machined with a number of micro-grooves, which are used to assemble micro-channels as micro reactors for chemical reaction applications. The experimental investigation shows that the overlap of different scales of structures within the channels greatly affects the micro fluidic behavior, and in turn helps to enhance the reaction rates [9].

Since obvious relationship among surface structure, morphology features and their corresponding functional properties is observed, there is an increasing need to have an effective control strategy over the geometric features not only at macroscopic level, but also at microscopic level. That is to say, industries are looking forward to designing geometric features at multi-scale levels for functional surfaces to meet specific functional requirements first, and then to define appropriate processes and fabrication parameters for manufacturing. For a long time, due to the lack of geometric modelling support, microtopography over machined surfaces are regarded as roughness and described by means of statistic data. Typical parameters such as R_a (arithmetic mean deviation of heights, measured on profiles), and others are used to describe the surface roughness at microscopic scale. However, these representations are hard to reveal the complicated details and exact nature of these geometric features at microscopic level. More importantly, in many applications, these micro geometric features are a part of surface morphology and constitute the dominative factor to determine the functional properties of the surface.

Fig.1 Multi-scale structures on micro grooves for chemical reaction enhancement: (a) Macro structures; (b) Substructures; (c) Micro- topography

There are many powerful modelling products commercially available for industrial product design and manufacturing. However, most of the current geometric modelling techniques are initially developed for macro geometries in Euclidean space. Therefore, classical Euclidean geometry is hardly of any help in modelling irregular geometries that are important features and natural patterns over most functional surfaces, like the microtopography. Moreover, the number of features to be modelled, in a typical multi-scale functional surface, easily outnumbers the capabilities of the most powerful commercial CAD system. In this connection, the incapability of classical geometry modelling techniques to describe the real micro-scale world has led to the novel concept of “fractal geometry”, which fills the gap. With fractal geometry modelling technique, it is now possible to model a family of shapes that are continuous but not differentiable everywhere.

3 Theory and solution

3.1 Fractal geometry theory and application in rough surface modelling

The theory of fractal geometry was initially proposed by MANDELBROT in 1967 [11] to investigate the coastlines of Britain. Since then, it gets fast development over the past decades. In mechanical engineering field, the fractal geometry approach becomes an efficient tool for surface morphology representation and analysis in tribology related research. The use of fractal geometry approach is based on the observation that the morphology of most machined surfaces is statistically self-affined [12], which implies that when the morphology is magnified properly, more roughness details would emerge and appear similar to the original profile, i.e., the roughness at all magnifications appears quite qualitatively similar in structure (Fig.2).

From the fractal geometry point of view, the profile of a surface, R(x), can be assumed to be continuous but non-differentiable everywhere. Such mathematical properties are satisfied by the W-M function given by

 (1<D<2,γ>1)         (1)

where A is a scaling constant; D is the self-affined fractal dimension for profiles; A and D are independent of the resolution of the scan instruments and scales. n is a frequency index; φ_n is a random phase; γ is the scaling parameter to determine the spectral density and self property in the profile. In the roughness investigation, based on considerations of surface flatness and density of frequency distribution, γ is normally chosen to be 1.5.

We use  and  to specify the low and high cut-off frequencies in the W-M function, respectively. n_max is actually the number of cosine shapes added for a profile. When n_max→∞, Eq.(1) turns to be the mathematical representation of the real fractal geometry. In fact, for practical applications, a finite range of spectrum is used for simulation. ω_l is provided by sample length L_s as ω_l=1/L_s, and ω_h is related with the resolution of scan instrument δ as ω_h=1/2δ. The random phase φ_n is used to prevent the coincidence of different frequencies at any point of the profile.

Fig.2 Statistical self-affinity for functional surface profile with magnification: (a) Observation in 2D space; (b) Observation in 3D space

Given σ to represent the root-mean-square (rms) roughness height of a profile, the scaling constant can be determined as

                      ⁽²⁾

where A is a scaling constant; D is the self-affined fractal dimension for profiles; A and D are independant of the resolution of the scan instruments and scales.

Therefore, once D and σ are determined, a more realistic characterization of rough profile at micro-level can be derived based on W-M fractal representation .

The above basic W-M fractal model can be extended to model the fractal rough surface in 3D space using

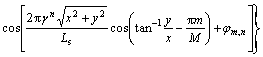(3)

                                         (4)

where  has the same physical meaning and magnitude as that in Eq.(1), and D_s (2s<3) is the fractal dimension of the surface. The physical meaning of D_s is the extent of space occupied by the rough surface. The value of D_s can be determined from the slope of the log-log plot of the power spectrum. The parameter M denotes the number of superposed ridges used to construct the surface. Taking the surfaces possessing cylindrical corrugation as an example, their representations are with M=1. G is the height scaling parameter derived from parameter A, A=2π(2π/G)^2-D, which is also independent of the frequency of distribution.

3.2 Synthesis of W-M fractal roughness with parametric profiles

It is well recognized that the rough surfaces on machined parts exhibit fractal features. However, most current researches are focused on the fractal measurement and description for planar surfaces. In other words, these models are not applicable for rough surfaces with freeform profiles. As a matter of fact, coming with freeform shapes at macro-scale by nature, most functional surfaces are usually modelled based on implicit representation (e.g. conic equations) or parametric representation (such as NURBS or Bezier splines). The fractal geometry itself offers little control over macro shape, therefore, the synthesis of fractal geometry approach for freeform macro shape modelling offers a feasible solution to the problem of functional surface modelling. One of the successful examples is the fractal based roundness modelling approach for cylindrical object recently developed by YOON and CHIN [13]. However, for the synthesis of fractal geometry with more general freeform shapes, conventional approaches are used to tessellate freeform surfaces into a set of planar meshes first, and then the fractal texture is added by recursively subdividing and randomly perturbing the mesh elements. Unfortunately, such approaches produce annoy visual artifacts because the spatial statistics varies across the original mesh boundaries.

In the W-M function of Eq.(1), the variable x represents the linear distance along X axis while z(x) is the corresponding roughness height along Z axis. The equation is valid for the simulation of fractal roughness over linear or planar profile. However, the micro fractal features of machined surfaces actually happen independently from the macro geometry of the surface, but are solely affected by local geometric property. Therefore, in this work, the microtopography of a surface is the combined result of the micro fractal profile R(x) in Euclid space against underlying freeform profile C(u) in parametric space. To facilitate this combination, the nature parameter, S, which is the accumulated arc length along a parametric curve, is proposed to be a unified variable for the two profiles. That is to say, the R(x) and C(u) should be at first converted into the unified parametric space, and then the two profiles are synthesized. As illustrated in Fig.3, instead of using R(x), now ΔR(s) (Eqs.(3)-(6)) is used to represent the local roughness profile against the given curve C(s) along the normal vector N(s) of the curve. Thus, the fractal curve F(s) is the synthesis result, which is a multi-scale model including both macro shape and micro topography details. F(s) is represented as

F(s)=C(s)+N(s)??R(S(u))                                              (5)

 (1<D<2, γ>1)      (6)

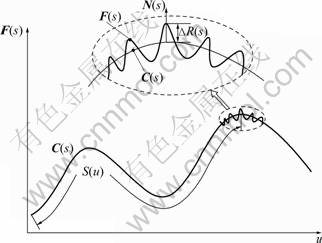
Fig.3 Synthesis of fractal roughness profile with parametric curve

In some fractal synthesis applications with conic curve profiles, the nature parametric equation can be exactly obtained from its conventional parametric equation by algebraic derivation. Equations (3)-(7) give an example of parametric ellipse curve representation:

C(u)=[a?cos(u), b?sin(u)]  (u₀1)                           (7)

The arc length S can be obtained by the following integral computation,

                                               (8)

and 

C′(u)=[-a?sin(u), b?cos(u)]                                           (9)

                                                 (10)

                                                      (11)

Thus, the nature parametric C(s) can be obtained as

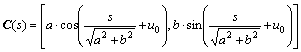(12)

However, theoretically, it is not possible to directly represent arc-length parameterization for cubic splines, which is the generic representation for freeform profiles. A parametric representation of a cubic spline curve is given as

C(u)=[x(u), y(u), z(u)]  (u₀<u<u­)   (13)

where

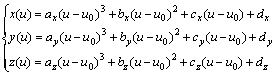  (14)

The arc length is a geometric integration, which in general cannot be computed analytically. Its representation is

             (15)

Therefore, the arc-length parameterization for cubic spline curves cannot be expressed as a combination of elementary functions and must be evaluated numerically. A number of numerical methods are developed to approximately compute arc-length parameterizations of spline curves. The integral formula (Eqs.(15)) to compute arc length S(u) can be approximated with conventional numerical integration methods such as Gaussian quadrature or Simpson’s rule. In order to provide a means to control the accuracy of the approximation, GUENTER and PARENT [14] developed a multi-step method named adaptive Gaussian integration. It divides the interval of integration in half and integrates each sub-interval separately. The sum of the integrals computed on the two sub-intervals is then compared with the value computed over the entire interval. If the difference between them is less than a desired accuracy, then the procedure returns to the sum of the two halves; otherwise it recursively applies the procedure on the sub-intervals. In this work, this numeric approach is adopted for the fractal interpolation with CAD models.

Compared with existing analytic approach for conic profiles, the numeric approach is approximate but robust. Its algorithm is generic for both conic profiles and higher order spline profiles with controllable parameterization error. The relationship between segment approximation accuracy and parameterization error was investigated [15]. At this preliminary research stage, it is not convenient yet to quantitatively evaluate the influence of the accuracy on the topography simulation. However, from the simulation experiments conducted, its influence on the fractal local profile is not sensitive and hence can be ignored.

Figure 4 gives the comparison of fractal geometry synthesis along machined profiles, where the simulated roughness profile A is generated based on the proposed arc-length parametric approach. Profile of Case B is the result by evaluating the W-M fractal curve in the same parametric space of spline C(u), which can be observed. The comparison shows that fractal roughness distribution is obviously affected by the macro geometry, and is not uniform.

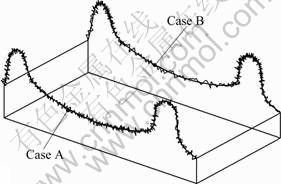
Fig.4 Comparison example for synthesis W-M fractal profile with spline curves (Case A: based on arc-length parametric; Case B: without using arc-length parametric)

The above approach can be extended to the application of fractal synthesis with parametric surfaces in three-dimensional space, as illustrated in Eq.(16). Some examples of the surface microtopography generated by the approach with specific parametric controls are given in Fig.5, where Figs.5(a)-(c) demonstrate the influence of fractal dimension D_s on microtopography, and Figs.5(d)-(f) demonstrate the impact of coefficient G on the roughness features of the surface.

(16)

Fig.5 Examples of microtopography control on spline surfaces: (a)-(c) Influence of fractal dimension D_s on microtopography; (d)-(f) Impact on surface roughness features by G; (a) G=0.013 6 mm, M=1; γ=1.5, D_s=2.2; (b) G=0.013 6 mm, M=1; γ=1.5, D_s=2.5; (c) G= 0.013 6 mm, M=1; γ=1.5, D_s=2.8; (d) G=0.003 6 mm, M=1; γ=1.5, D_s=2.5; (e) G=0.023 6 mm, M=1; γ=1.5, D_s=2.5; (f) G=0.033 6 mm, M=1; γ=1.5, D_s=2.5

3.3 Implementation and case studies

3.3.1 Platform and implementation

The proposed fractal synthesis approach is implemented into a value-added module, namely fractal.arx module, which is developed based on ObjectARX 2008? using Visual C++ 2005, and runs in the same process as AutoCAD and has direct access to AutoCAD internal database and graphics. The object hierarchy for implementing fractal synthesis with B-rep models is illustrated in Fig.6. With loading of the fractal.arx module, fractal modelling commands can be used in exact the same way as native AutoCAD commands. The ObjectARX platform provides versatile sets of tools of geometric and graphics support for application developers to take advantages of the open architecture of AutoCAD software. For example, the library of AcBr.lib (AutoCAD boundary representation query library) is provided to support full access of the B-rep structures of solid models, with which custom fractal geometry applications can be built fast and efficiently, since the developer just needs to focus on the design and implementation of fractal geometry related algorithms. With this value-added module, users can create three-dimensional solid models either using AutoCAD’s own solid modelling functions, or importing SAT files from other solid modelling systems.

3.3.2 Visualization optimization

Based on the recursive algorithm, a fractal surface brings plenty of topography information at different scales. Theoretically, fractal surfaces generated by W-M function are non-differentiable everywhere. This indicates that the recursion is supposed to be infinite. The recursive algorithm for generating fractal surfaces can easily generate millions of geometry primitives for rendering that most common graphics hardware cannot afford. In other words, the on-line processing time of this huge number of primitives for visualization would make it impossible to allow real-time user interaction. In this work, two optimization strategies, namely adaptive recursion for reasonable visualization and runtime visibility culling, have been specifically developed to support runtime fractal detail visualization.

The idea of visualization optimization is based on the facts that only limited details of a fractal surface can be observed within a specific viewing screen due to its pixel resolution, and only limited portion of a fractal surface can be visualized when it is recursively zoomed in for fractal details. Each pixel in screen corresponds to a space unit in viewing volume. As illustrated in Fig.7(a), when the size of a fractal segment generated by a recursion step, N, is smaller than the size of a space unit, the recursion stops since the graphic output of further fractal details is unnecessary for viewing. In this connection, the recursion depth is adaptive subjected to to current zooming scale.

With increasing zooming scale for more detailed viewing, the fractal recursion goes further and generates more detailed fractal segments for visualization, which brings tremendously increasing number of fractal segments for rendering. As already mentioned, for a zoom in operation, very limited portion of a fractal surface is visible, and the visible portion will decrease with each following zoom-in operation. This constitutes the main advantage of applying visibility culling approach for further visualization optimization. With visibility culling, geometry primitives out of current viewport from the rendering process can be culled away. The proposed runtime visibility culling approach is based on the spatial subdivision of fractal surfaces. As illustrated in Fig.7(b), according to its density of resolution, a fractal surface is partitioned into a number of square patches with tessellated nodes. And then, the interference status with viewing volume for each node is checked. Instead of using the precise geometry of surface patch for interference computation, a simplified geometry of oriented bounding volume is used to fast test the interference for each node. If no interference exists, there is no need to send the fractal segments under the node to graphics pipeline for rendering.

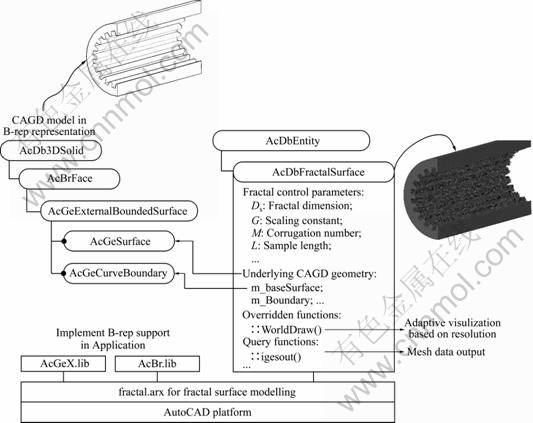
Fig.6 Object hierarchy for implementing fractal synthesis with B-rep models based on Object ARX platform

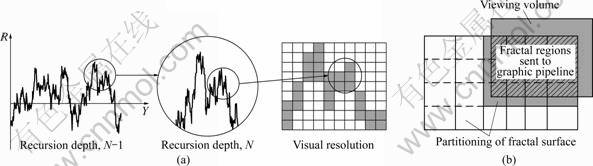
Fig.7 Visualization optimization approaches: (a) Adaptive recursion for reasonable visualization; (b) Runtime visibility culling

As illustrated in Fig.6, on top of AcDbEntity, the AutoCAD’s base class for graphic entities, a new class, namely AcDbFractalSurface, is derived to represent fractal surfaces integrating with CAGD faces. The AutoCAD graphics class worldDraw() is overridden by implementing fractal graphics display based on the optimization strategies.

3.3.3 Database residence and mesh output

The fractal surface object of AcDbFractalSurface is a database residence object, which can be registered with AutoCAD core database and saved with the opular .DWG format. Its own date members are fractal control settings only. This makes the object itself occupy very small storage space, even though it can present a very complicated geometry details. The application does not save the fractal mesh with AutoCAD database or as .DWG drawing, but allows users to output the mesh data with desired resolution through STL or IGES data exchange interfaces for further simulation or computation purposes.

Based on the implemented module, a few multi- scale modelling examples are demonstrated in Fig.8, of which (b) and (d) are for the case of micro-channel array functional surfaces, while (e) and (f) are for heat pipes.

4 Conclusions

1) A mathematic modelling approach is proposed for the synthesis of W-M fractal geometry in micro space and common CAGD models in macro space. With the fractal geometry based model, a functional surface can be precisely modelled in multiple scales from its overall macro shape to micro roughness details. This integrated modelling constitutes the main contribution of the work. Although the synthesis model proposed in this work cannot be considered as a universal model for all types of functional surfaces, it does provide a fairly complete and consistent description for applications with freeform surfaces at macro scale.

2) The multi-scale modelling approach is implemented into a value-added executable module based on Autodesk’s ObjectARX 2008 platform and Visual C++ 2005. Instead of saving these fractal segments into database, in this work, the fractal surface geometry is generated dynamically for visualization, which guarantees a smart database format for less computational efforts.

3) To support the runtime visualization, two optimization strategies, namely runtime visibility culling and adaptive recursion for reasonable visualization, are developed specifically to prevent unnecessary fractal elements from visualization. The visualization optimization greatly reduces graphics load and enables the runtime visualization of the surfaces details in multiple scales.

4) A consistent mathematic model is establised to represent multi-scale surface geometries. Further research is expected to reveal the association between functional behaviors and topography property of the surface at multiple scales, so that design optimization can be conducted according to specific functional requirement.

Fig.8 Examples of microtopography synthesis for functional surfaces: (a) Fractal surface simulation with AutoCAD/Object ARX 2008; (b) SEM image of functional surface with micro-channel array; (c) Simulated functional surface from top view; (d) Simulated functional surface from isometric view; (e) SEM image of heat pipe sample; (f) Fractal simulation for rough surface of heat pipe

References

[1] QU J, WU H, CHENG P. Effects of functional surface on performance of a micro heat pipe [J]. International Communications in Heat and Mass Transfer, 2008, 35(5): 523-528.

[2] NONINO C, COMINI G. Convective heat transfer in ribbed square channels [J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2002, 12(5): 610-628.

[3] GOODSON K E, KURABAYASHI K, PEASE R F W. Improved heat sinking for laser-diode arrays using microchannels in CVD diamond [J]. IEEE Transactions on Components Packing and Manufacturing Technology Part B, 1997, 20(1): 104-109.

[4] NUNO N, GROPPETTI R, SENIN N. Static coefficient of friction between stainless steel and PMMA used in cemented hip and knee implants [J]. Clinical Biomechanics, 2006, 21(9): 956-962.

[5] PARK G G, YIM S D, YOUN Y G, LEE W Y, KIM C S, SEO D J, EGUCHI K. Hydrogen production with integrated microchannel fuel processor for portable fuel cell systems [J]. Journal of Power Sources, 2005, 145(2): 702-706.

[6] SENIN N, GROPPETTI R. Surface microtopography design and manufacturing through topography descriptors: An application to prosthetic implant surfaces [J]. Computer-Aided Design, 2005, 37(11): 1163-1175.

[7] HANNSON S, NORTON M. The relation between surface roughness and interfacial shear strength for bone-anchored implants: A mathematical model [J]. Journal of Biomechanics, 1999, 32(8): 829-836.

[8] ABRON A, HOPFENSPERGER M, THOMPSON J, COOPER L F. Evaluation of a predictive model for implant surface topography effects on early osseointegration in the rat tibia model [J]. Journal of Prosthetic Dentistry, 2001, 85(1): 40-46.

[9] CHEN Y P, ZHANG C P, SHI M H, PETERSON G P. Role of surface roughness characterized by fractal geometry on laminar flow in microchannels [J]. Physical Review E, 2009, 80(2): 026301.

[10] MANDELBROT B B, PASSOJA D E, PAULLAY A J. Fractal character of fracture surfaces of metals [J]. Nature, 1984, 308: 721-722.

[11] MANDELBROT B B. How long is coast of Britain? Statistical self-similarity and fractional dimension [J]. Science, 1967, 156(3775): 636-638.

[12] MAJUMDAR A, TIEN C L. Fractal characterization and simulation of rough surfaces [J]. Wear, 1990, 136(2): 313-327.

[13] YOON M C, CHIN D H. Fractal roundness modelling of a measured profile of a cylindrical object [J]. International Journal of Advanced Manufacturing Technology, 2008, 35(11/12): 1156-1165.

[14] GUENTER B, PARENT R. Computing the arc length of parametric curves [J]. IEEE Computer Graphics and Applications, 1990, 10(3): 72-78.

[15] WANG H, KEARNEY J, ATKINSON K. Arc-length parameterized spline curves for real-time simulation [C]// The 5th International Conference on Curves and Surfaces. France: San Malo, 2002: 387-396.

(Edited by YANG Bing)

Foundation item: Projects(50975092, 50805052, U0834002) supported by the National Natural Science Foundation of China; Project(9151030101000007) supported by the Natural Science Foundation of Guangdong Province, China; Project(2009ZZ0041) supported by the Fundamental Research Funds for the Central Universities in China

Received date: 2010-08-02; Accepted date: 2010-10-29

Corresponding author: LI Jing-rong, Associate Professor; Tel: +86-20-87110132; E-mail: Catherine.JRLi@gmail.com