Trans. Nonferrous Met. Soc. China 27(2017) 148-156

First-principles investigations of structural, mechanical, electronic and optical properties of U₃Si₂-type AlSc₂Si₂ under high pressure

Xu-dong ZHANG¹, Feng WANG², Wei JIANG^1,2

1. School of Science, Shenyang University of Technology, Shenyang 110870, China;

2. School of Materials Science and Engineering, Shenyang University of Technology, Shenyang 110870, China

Received 10 December 2015; accepted 15 August 2016

Abstract: The structural, elastic, electronic and optical properties for U₃Si₂-type AlSc₂Si₂ compound under pressure were systematically investigated by using the first-principles calculations. The values of elastic constants and elastic moduli indicate that AlSc₂Si₂ keeps mechanical stability under high pressure. The mechanical properties of AlSc₂Si₂ are compared with those of Al₃Sc. The results indicate that AlSc₂Si₂ is harder than Al₃Sc. Anisotropic constant A^U and 3D curved surface of elastic moduli predict that AlSc₂Si₂ is obviously anisotropic under pressure. The electronic structure of AlSc₂Si₂ exhibits metallic character and the metallicity decreases with the elevated pressure. In addition, optical properties as a function of pressure were calculated and analyzed. The present work provides theoretical support for further experimental work and industrial applications.

Key words: U₃Si₂-type AlSc₂Si₂; mechanical properties; electronic structure; optical properties; first-principles calculations

1 Introduction

The L1₂-type Al₃Sc precipitates can form a stable and fine-grain structure and block the mobile dislocations. The outstanding physical features make Al-based alloys with Sc element have excellent mechanical properties with elevated temperature. Al₃Sc intermetallics have been deemed as an effective strengthening phase in the development of novel Al-based alloys [1-7]. The physical properties of Al₃Sc have been investigated extensively over the past twenty years, such as mechanical properties [8-16], electronic properties [16-20], thermodynamic and optical properties [21-24]. The addition of Si element into Al-Sc alloys reduced the amount of Al₃Sc precipitates. The Al-Si-Sc alloys trend to form the V-phase (AlSc₂Si₂) in the isothermal section of the phase diagram [25]. ZHANG et al [26] used the scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) and found that the AlSc₂Si₂ precipitates were adjacent to the grain boundary in the Al-Si-Sc alloys. The AlSc₂Si₂ precipitates have caused significant changes in the microstructure and mechanical properties in the Al-Sc alloys [26,27]. For the physical properties of AlSc₂Si₂, the first-principles calculations have been used to investigate the formation enthalpy, elastic constants and density of states [28]. However, to the best of our knowledge, many physical properties of AlSc₂Si₂ are not well investigated under high pressure. The available reports are not enough to systematically understand the physical properties of AlSc₂Si₂. So, in the present work, the physical properties of AlSc₂Si₂ were systematically investigated by using the first-principles calculations.

2 Computation methods

The present calculations were performed with the first principles method based on the pseudopotential plan-wave within density functional theory (DFT) using Cambridge Serial Total Energy Package (CASTEP) [29] code. Ultrasoft pseudo-potentials were used to model the ion-electron interaction. The exchange and correlation potentials were described with the generalized gradient approximation (PBE-GGA). Pseudo-atomic calculations were performed for Sc 3s²3p⁶3d¹4s², Si 3s²3p² and Al 3s²3p¹. Tests of the convergence can be obtained with cutoff energy of 400 eV and the Monkhorst-Pack special k-point scheme with 8×8×14 grid meshes in the Brillouin zone. We used the Pulay scheme of density mixing for the evaluation of energy and stress. In the meantime, the tolerance of the geometry optimization was set to be less than 5.0×10^-6 eV/atom. The maximum ionic Hellmann- Feynman force, ionic displacement and stress were 0.001 eV/, 0.0005  and 0.03 GPa, respectively. We used the tetrahedron Bloch method with corrections to calculate electronic structure. The SCF tolerance was set to be 5.0×10^-6 eV/atom. The stress-strain method [30] was used to calculate elastic constants of AlSc₂Si₂.

Fig. 1 Crystal structure of tetragonal AlSc₂Si₂

3 Results and discussion

3.1 Structural properties

The ternary compound AlSc₂Si₂ has tetragonal U₃Si₂ crystal structure with space group P4/mbm (No. 127). In the unit cell of AlSc₂Si₂, Al atom occupies the Wyckoff site 2a (0, 0, 0), Sc atom occupies the Wyckoff site 4h (0.1786, 0.6786, 0.5) and Si atom occupies the Wyckoff site 4g (0.3692, 0.8692, 0), as shown in Fig. 1. The total energy of AlSc₂Si₂ as a function of the volume was calculated. The ground state structural parameters and pressure-volume curve can be obtained by fitting the data of energy vs volume to the Birch-Murnaghan equation of state [31], in which the pressure-volume relationship is expressed as

     (1)

where f_E=1/2[(V₀/V)^2/3-1], B′=dB/dP and B₀ are hydrostatic bulk modulus, the pressure derivative of the bulk modulus and zero pressure bulk modulus, respectively. The ground state structural parameters are listed in Table 1, along with the available experimental and theoretical values. The calculated results are very close to the values of the available experiments and theoretical calculations [28,32]. This indicates that the computation method is reliable. To investigate the influence of pressure on the crystal structure for AlSc₂Si₂, the curves of the lattice parameters (a/a₀, c/c₀) and unit cell volume ratio (V/V₀) of AlSc₂Si₂ with pressure are plotted in Fig. 2. The ratios of a/a₀, c/c₀ and V/V₀ decrease with the increase of pressure. The polynomial function relationships of a/a₀, c/c₀ and V/V₀ are

a/a₀=0.9997-0.0050P+1.2281×10^-4P²           (2)

c/c₀=1.0005-0.0091P+1.2438×10^-4P²     (3)

V/V₀=1.0002-0.0032P+4.3810×10^-5P²           (4)

Equations (2) and (3) reveal that AlSc₂Si₂ is compressible along a axis and c axis. In Fig. 2, the ratios of the lattice parameters and volume at 30 GPa decrease by about 9%, 6% and 18%, respectively. However, with the elevated pressure, the distance between atoms becomes smaller due to the stronger repulsive interaction among atoms, which leads to the compression more difficult under high pressure.

Table 1 Calculated lattice constant bulk modulus B₀ and its first pressure derivative of AlSc₂Si₂ compared with other theoretical calculations and experiments at 0 GPa

Fig. 2 Variations of ratios, a/a₀, c/c₀ and V/V₀, of AlSc₂Si₂ as function of pressure

3.2 Mechanical properties

For the tetragonal crystalline, AlSc₂Si₂ has six independent elastic constants, that is, C₁₁, C₃₃, C₄₄, C₆₆, C₁₂ and C₁₃. The calculated elastic constants are listed in Table 2 and are consistent with the theoretical values [28]. The calculated elastic constants versus pressure are plotted in Fig. 3. The calculated elastic constants C_ij of AlSc₂Si₂ exhibit similar tendency and increase almost linearly with the increasing pressure from 0 to 30 GPa. These elastic constants satisfy traditional mechanical stability conditions [33], C₁₁- C₁₂>0, C₁₁>0, C₃₃>0, C₄₄ >0, C₆₆ >0, C₁₁+C₃₃-2C₁₃>0, 2(C₁₂+C₁₁)+C₃₃+4C₁₃>0, indicating that AlSc₂Si₂ is mechanically stable for the considered pressure range. In Fig. 3, the elastic constants C₁₁ and C₃₃ are larger than others in the considered pressure range. This indicates that AlSc₂Si₂ is incompressible under uniaxial stress along the z axis or x axis.

Table 2 Calculated elastic constants of AlSc₂Si₂ at 0 GPa

Fig. 3 Calculated elastic constants, C_ij, under different pressures

The mechanical properties are mainly determined by the elastic moduli, including Poisson ratio v, shear modulus G, elastic modulus E and bulk modulus B. These moduli are calculated in term of the elastic constants C_ij using the following formulas [34]:

                             (5)

                             (6)

                               (7)

                                 (8)

For tetragonal crystal [35]:

           (9)

B_R=C²/M                                   (10)

G_V=(M+3C₁₁-3C₁₂+12C₄₄+6C₆₆)/30            (11)

G_R=15/[18B_V/C²+6/(C₁₁-C₁₂)+6/C₄₄+3/C₆₆]     (12)

where B_V and G_V are the Voigt’s bulk and shear modulus, respectively; B_R and G_R are the Reuss’s bulk and shear modulus, respectively. The calculated elastic moduli at 0 GPa are listed in Table 3 along with the available values [28]. The obtained mechanical moduli (B, G, E) of AlSc₂Si₂ under high pressure are plotted in Fig. 4. These moduli also exhibit similar variation tendency and increase almost linearly with increasing pressure from 0 to 30 GPa. In Fig. 4, the values of B are larger than those of G in the whole pressure range. This indicates that the parameter limiting the stability of AlSc₂Si₂ under high pressure is the shear modulus [36]. In Fig. 4, we provide the mechanical data for Al₃Sc [15]. The mechanical properties of U₃Si₂-type AlSc₂Si₂ are compared with those of the cubic Al₃Sc. The elastic moduli B, G, E of AlSc₂Si₂ are all larger than those of Al₃Sc under pressure from 0 to 30 GPa, respectively. The results indicate that AlSc₂Si₂ is harder to compress than Al₃Sc. The value of B/G is related to the brittleness and ductile of materials. The critical value which separates ductile and brittle material is 1.75; i.e., if B/G>1.75, the material behaves in a ductile manner; otherwise, the material will have a brittle manner [32]. In Table 3, we can see that the result of B/G is smaller than 1.75 at 0 GPa, which indicates that AlSc₂Si₂ is the brittle material.

Table 3 Calculated elastic moduli B, G, E, v, B/G and anisotropy index A^U at 0 GPa

Fig. 4 Bulk modulus, shear modulus and elastic modulus under different pressures

In Fig. 5, the values of B/G of AlSc₂Si₂ increase with the elevated pressure, indicating that the pressure can reduce the brittleness of AlSc₂Si₂. Figure 5 also provides the relationship between Poisson ratio and pressure. The values of v increase with the elevated pressure. Poisson ratio v can provide some useful information about the properties of bonding forces. The upper limit for central force of solids is 0.5 and the lower limit is 0.25. In the present work, the value of v is 0.211 at 0 GPa, which is smaller than the lower limit, which indicates that the inter-atomic forces of AlSc₂Si₂ are not central forces. The values of v increase with elevated pressure and become beyond the lower limit values of 0.25 under pressure from 15 to 30 GPa, indicating that the inter-atomic forces of AlSc₂Si₂ become central forces under pressure from 15 to 30 GPa.

Fig. 5 Calculated Poisson ratio (a) and B/G (b) under different pressures

Elastic anisotropy constant is an important physical parameter of materials and has many industrial and technological applications. Based on the obtained elastic constants and moduli, we calculated universal elastic anisotropy index A^U to estimate the anisotropy of AlSc₂Si₂. The universal elastic anisotropy index, A^U, was proposed as follows [37]:

                      (13)

The universal elastic anisotropy index, A^U, is equal to zero, namely, the crystal with the value of A^U=0 is elastically isotropic. At 0 GPa, the A^U of AlSc₂Si₂ is 0.565 and obviously deviates from 0, indicating that it is anisotropic. Figure 6 shows the relationship between A^U and pressure. The values of A^U increase with the elevated pressure. However, the values of A^U are in the range of 0.565-0.613 from 0 to 30 GPa and the anisotropic content shows little change. For comparison, the values of A^U of Al₃Sc from Duan’s work [20] are plotted in Fig. 6. The values of A^U are in the range of 0.002-0.0375 from 0 to 30 GPa and are all close to 0, indicating that Al₃Sc basically keeps isotropic in the whole pressure range. In order to further treat the elastic anisotropy, the three-dimensional curved surfaces of elastic modulus in given direction are plotted. The 3D elastic modulus surface can be determined by using the following equations [38,39].

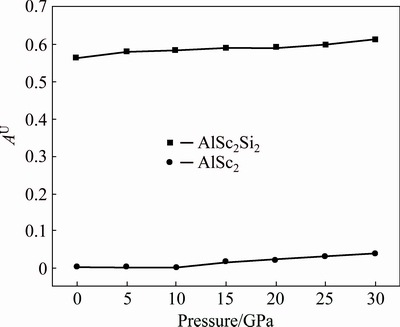
Fig. 6 Anisotropy coefficient A^U of AlSc₂Si₂ and Al₃Sc under different pressures

For cubic crystal structure,

   (14)

For tetragonal crystal structure,

                   (15)

where S_ij is the elastic compliance constant and l₁, l₂ and l₃ are the direction cosines. For an isotropic crystal, the 3D curved surface would exhibit a spherical shape and the deviation degree from the spherical surface indicates the contents of anisotropy. We calculated elastic compliance constants S_ij and obtain the 3D elastic modulus surface. The 3D figures of Al₃Sc and AlSc₂Si₂ at 0 and 30 GPa are plotted in Fig. 7. In Fig. 7, the 3D surfaces of the Al₃Sc at 0 and 30 GPa are obviously in spherical shape and exhibit a noticeable isotropy.

Fig. 7 Directional dependence of elastic modulus for Al₃Sc (a, b) and AlSc₂Si₂ (c, d) under pressures

However, we can note that the deviation degrees from the spherical surface of AlSc₂Si₂ are obviously larger than those of Al₃Sc, which indicates that AlSc₂Si₂ has stronger anisotropy than Al₃Sc in different directions. In the meantime, the contents of deviation show little change with elevated pressure. These results are also consistent with the analysis of anisotropy factors A^U under pressure.

Fig. 8 Band structure of AlSc₂Si₂ at 0 GPa

Fig. 9 Partial and total density of states of AlSc₂Si₂ at 0 GPa

Fig. 10 Total density of states of AlSc₂Si₂ at different pressures

3.3 Electronic properties

The electronic band structure for AlSc₂Si₂ was calculated using the equilibrium lattice parameters and shown in Fig. 8. The conduction and valence bands obviously overlap and there is no energy gap around the Fermi level, which indicates that AlSc₂Si₂ exhibits a metallic character. The total density of states and partial density of states for AlSc₂Si₂ are shown in Fig. 9. The value of density of states at Fermi energy is nonzero, which also confirms that AlSc₂Si₂ has metallic character. In the meantime, the density of states is mainly dominated by the hybridization of Al 3s, Al 3p and Si 3s states from -11.883 to -6 eV. From -6 eV to 0 eV, the energy binding states are dominated by Al 3p, Si 3p and Sc 3d states. In the conduction region, the electronic structure is also dominated by Al 3s, Al 3p, Si 3p and Sc 3d states. Figure 10 shows the total density of states under pressure. The energy regions around Fermi level are from -11.883 to 4.227 eV, from -12.409 to 4.773eV, from -12.801 to 5.152, and from -13.095 to 5.398 eV at 0, 10, 20 and 30 GPa, respectively. In Fig.10, the profile of total density of states shows little changes, which means that the structure of AlSc₂Si₂ keeps structural stability up to 30 GPa. Moreover, the total density of states decreases with the elevated pressure. The calculated values of the total density of states at Fermi level are 3.255, 2.957, 2.946 and 2.898 state/eV at 0, 10, 20 and 30 GPa, respectively. This is because the distance between atoms under high pressure becomes smaller and gives rise to the change of the interaction potentials. A pseudo-gap exists around Fermi level and pseudo-gaps become wider with the elevated pressure. It is concluded that the covalent bond increases with the elevated pressure. Generally speaking, the wider pseudo-gap represents the stronger covalent bond [40]. In the meantime, we also estimate the metallicity of AlSc₂Si₂ compound by following equation [41]: f_m=0.026D_f/n_e, where n_e is the valence electron density of the cell and D_f is the value of the density of states at Fermi level. The calculated values of f_m are 0.1138, 0.1052, 0.1023 and 0.1005, at 0, 10, 20 and 30 GPa, suggesting that the metallicity of AlSc₂Si₂ decreases with elevated pressure.

3.4 Optical properties

To further investigate the physical properties, the optical parameters are calculated, including the dielectric function ε(ω), the refractive index n(ω) and the extinction coefficient k(ω). These optical parameters can be obtained by the complex dielectric function ε(ω): ε(ω)=ε₁(ω)+iε₂(ω). ε₁(ω) and ε₂(ω) are the real part and imaginary part of the complex dielectric function. The refractive index n(ω) and extinction coefficient k(ω) using ε₁(ω) and ε₂(ω), are calculated through the following equations [42]:

        (16)

        (17)

Figures 11 and 12 provide the optical properties in the energy range of 0-20 eV. There are no experimental data for AlSc₂Si₂. The calculated results will provide theoretical support for further experimental work and industrial applications. In Fig. 11, the values of the real part and imaginary part are close to zero and change very little in a high energy region. The main peak of imaginary part appears around 0.97 eV and originates predominantly from the direct optical transitions between Sc 3d states and Al 3s states. The curve of the real part declines linearly with elevated energy from 0 to 4 eV. Figure 12 shows the calculated refractive index n(ω) and extinction coefficient k(ω) for AlSc₂Si₂. Generally speaking, the square of refractive index n(ω) is proportional to dielectric constant ε₁(ω). Larger dielectric constant represents larger refractive index. So, the shape of curves of the refractive index n(ω) and dielectric constant ε₁(ω) is similar to each other. The main peak of extinction coefficient k(ω) appears around 2.75eV and then declines linearly with elevated energy to 12.7 eV.

Fig. 11 Real part and imaginary part of dielectric function for AlSc₂Si₂

Fig. 12 Calculated refractive index and extinction coefficient for AlSc₂Si₂

The pressure effects on static dielectric constant ε₁(0) and static refractive index n(0) for AlSc₂Si₂ are shown in Fig. 13. In Fig. 13, these parameters increase or decrease monotonically with increasing pressure from 0 to 30 GPa. We fit the calculated data to the quadratic polynomial and obtain the relationship between ε₁(0)/n(0) and pressure:

ε₁(0)=76.672+0.626P-0.0307P²     (18)

n(0)=8.779-0.0368P-0.0018P²      (19)

Fig. 13 Pressure dependence of static dielectric constant ε₁(0) (a) and static refractive index n(0) (b) for AlSc₂Si₂

Generally speaking, a simple relationship empirically links the mechanical properties of materials with their elastic modulus. The bulk modulus represents the resistance to volume change under pressure. The shear modulus represents the resistance to shape change caused by shearing force. In the meantime, the shear modulus plays more important role in determining the hardness of material. Elastic modulus is also a very important constant for the mechanical properties of materials. In Fig. 4, the values of the elastic moduli, B, G and E, of AlSc₂Si₂ are larger than those of Al₃Sc, indicating that AlSc₂Si₂ is harder to compress than Al₃Sc. AlSc₂Si₂ is the better strengthening phase than Al₃Sc. Meanwhile, Si element is cheaper than Sc, so adding Si to Al-Sc alloys can reduce the production costs of Al-Sc alloys.

4 Conclusions

1) The calculated structural data are very close to the values of the available experiment and calculation. The ratios of structural parameters a/a₀, c/c₀ and V/V₀ decrease with the increasing pressure.

2) AlSc₂Si₂ keeps mechanically stable under pressure from 0 to 30 GPa. The values of B, G and E under pressure increase with elevated pressure, suggesting that the crystal structure of AlSc₂Si₂ becomes more and more difficult to change with elevated pressure. The calculated anisotropic constants A^U and 3D curved surface of elastic modulus show that AlSc₂Si₂ is obviously anisotropic for considered pressure.

3) The calculated electronic structure shows that the AlSc₂Si₂ exhibits metallic character and keeps structural stability from 0 to 30 GPa. The pseudo-gap illustrates that the capacity of covalent bond becomes stronger.

References

[1] MARQUIS E A, HYDE J M. Applications of atom-probe tomography to the characterisation of solute behaviours [J]. Materials Science and Engineering R: Reports, 2010, 69: 37-62.

[2] MARQUIS E A, SEIDMAN D N. Nanoscale structural evolution of Al₃Sc precipitates in Al(Sc) alloys [J]. Acta Materialia, 2001, 49: 1909-1919.

[3] JIANG Zhong-tao, JIANG Bin, ZHANG Jian-yue, DAI Jia-hong, YANG Qing-shan, YANG Qin, PAN Fu-sheng. Effect of Al₂Ca intermetallic compound addition on grain refinement of AZ31 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1284-1293.

[4] XIAO Gang, YANG Qin-wen, LI Luo-xing. Modeling constitutive relationship of 6013 aluminum alloy during hot plane strain compression based on Kriging method [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 1096-1104.

[5] SEIDMAN D N, MARQUIS E A, DUNAND D C. Precipitation strengthening at ambient and elevated temperatures of heat-treatable Al(Sc) alloys[J]. Acta Materialia, 2002, 50: 4021-4035.

[6] RADMILOVIC V, OPHUS C, MARQUIS E A, ROSSELL M D, TOLLEY A, GAUTAM A. Highly monodisperse core-shell particles created by solid-state reactions [J]. Nature Materials, 2011, 10: 710-715.

[7] ZHOU Song, WANG Lei, XIE Li-yang, HU Li, XU Liang. Effect of T7951 secondary aging treatment on crack propagation behavior of 7055 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 938-944.

[8] DUAN Yong-hua, HUANG Bo, SUN Yong, PENG Ming-jun, ZHOU Sheng-gang. The phase stability, thermodynamics properties and electronic structures of L1₂-type Al₃Sc and Al₃Y under high pressures [J]. Chinese Physics Letter, 2014, 31: 088101.

[9] PAN Rong-kai, WANG Hai-chen, SHAO Lin, ZHENG Jie, PAN Xiong-zea, TANG Bi-yu. Temperature dependence of elastic properties of L12-Al3Sc: A first-principles study [J]. Computational Materials Science, 2016, 111: 424-429.

[10] MAO Z, CHEN W, SEIDMAN D N, WOLERTON C. First-principles study of the nucleation and stability of ordered precipitates in ternary Al-Sc-Li alloys [J]. Acta Materialia, 2011, 59: 3012-3023.

[11] WOODWARD C, ASTA M. Density of constitutional and thermal point defects inL1₂Al₃Sc [J]. Physical Review B, 2001, 63: 094103.

[12] XU J H, FREEMAN A J. Phase stability and electronic structure ofScAl₃andZrAl₃and of Sc-stabilized cubicZrAl₃precipitates [J]. Physical Review B, 1990, 41: 12553.

[13] HYLAND R W, STIFFLER R C. Determination of the elastic constants of polycrystalline Al₃Sc [J]. Scripta Metall Materials,1991, 25: 473-477.

[14] TIAN T, WANG X F, LI W. Ab initio calculations on elastic properties in L1₂structure Al₃X and X₃Al-type (X=transition or main group metal) intermetallic compounds [J]. Solid State Communications, 2013, 156: 69-75.

[15] GALAV K L, JOSHI K B. Ab initio investigations of structural and electronic properties of AlSc₃ [J]. International Journal of Computational Materials Science and Engineering, 2014, 3: 1450019.

[16] HU Wen-cheng, LIU Yong, LI De-jiang, ZENG Xiao-qin, XU Chun-shui. Mechanical and thermodynamic properties of Al₃Sc and Al₃Li precipitates in Al-Li-Sc alloys from first-principles calculations [J]. Physica B, 2013, 427: 85-90.

[17] SUN S P, LI X P,WANG H J,JIANG H F, LEI W N. First-principles investigations on the electronic properties and stabilities of low-index surfaces of L1₂-Al₃Sc intermetallic [J]. Applied Surface Science, 2014, 288: 609-618.

[18] WU Jian, WEN Li, TANG Bi-yu, PENG Li-ming, DING Wen-jiang. Generalized planner fault energies, twinning and ductility of L1₂type Al₃Sc and Al₃Mg [J]. Solid State Sciences, 2011, 13: 120-125.

[19] OKU M. SHISHIDO T, SUN Q, NAKAJIMA K, KAWAZOE Y. Comparison of electronic structures of ScAl₃and ScRh₃: X-ray photoelectron spectroscopy and ab initio band calculation [J]. Journal of Alloys and Compounds, 2003, 358: 264-267.

[20] DUAN Yong-hua, SUN Yong, PENG Ming-jun, ZHOU Sheng-gang. Ab-initio investigations on elastic properties in L1₂structure Al₃Sc and Al₃Y under high pressure [J]. Journal of Alloys and Compounds, 2014, 585: 587-593.

[21] LIN Dong-lin, CHEN Ping, YI Jian-xiong, TANG Bi-yu, PENG Li-ming, DING Wen-jian. Ab initiostudy on the thermal properties of the fcc Al₃Mg and Al₃Sc alloys [J]. Journal of Physics D: Applied Physics, 2009, 42: 225407.

[22] RESHAK A H, CHARIFI Z, BAAZIZ H. Ab-initio calculation of structural, electronic, and optical characterizations of the intermetallic trialuminides ScAl₃ compound [J]. Journal of Solid State Chemistry, 2010, 183: 1290-1296.

[23] LEE S J, PARK J M, CANFIELD P C, LYNCH D W. Optical properties and electronic structures of single crystalline RAl₃ (R=Sc,Yb, and Lu) [J]. Physical Review B, 2003, 67: 075104.

[24] CHEN Dong, CHEN Zhe, WU Yi, WANG Ming-liang, WANG Hao-wei. First-principles investigation of mechanical, electronic and optical properties of Al₃Sc intermetallic compound under pressure [J]. Computational Material Science, 2014, 91: 165-172.

[25] ROYSET J, RYUM N. Scandium in aluminium alloys [J]. International Materials Reviews, 2005, 50: 19-44.

[26] ZHANG Wen-da, LIU Yun, YANG Jing, DANG Jin-zhi, XU Hong, DU Zhen-min. Effects of Sc content on the microstructure of as-cast Al-7wt.%Si alloys [J]. Materials Characterization, 2012, 66: 104-110.

[27] ROTHLEUTNER L M,ROBERTC,CHESTERJVT. Influence of temperature and holding time on the interaction of V, Al, and N in microalloyed forging steels [J]. Metallurgical and Materials Transactions A, 2014, 45: 4549-4609.

[28] CHEN Dong, XIA Cun-juan, CHEN Zhe, WU Yi, MING Ming-liang, MA Nai-heng, WANG Hao-wei. Thermodynamic, elastic and electronic properties of AlSc₂Si₂ [J]. Materials Letters, 2015, 138: 148-150.

[29] SEGALL M D, LINDAN P D, PROBERT M J, PICKARD C J, HASNIP P J, CLARK S J, PAYNE M C. First-principles simulation: Ideas, illustrations and the CASTEP code [J]. Journal of Physics: Condensed Matter, 2002, 14: 2717-2743.

[30] HILL R. The elastic behaviour ofacrystalline aggregate [J]. Proceedings of the Royal Society of London: SeriesA, 1952, 65: 349-354.

[31] BIRCH F. Some remarks on the volume dependence of the Grüneisen parameter [J]. Journal of Geophysical Research, 1978, 83: 1257-1268.

[32] GHEBOULI B, GHEBOULI M A, FATMI M, LOUAIL L. First-principles calculations of structural, electronic, elastic and thermal properties of phase M₂SiC (M=Ti, V, Cr, Zr, Nb, Mo, Hf, Ta and W) [J]. Transactions of Nonferrous Metals Society of China.2015, 25: 915-925.

[33] WU Zhi-jian, ZHAO Er-jun, XIANG Hong-ping, HAO Xian-feng, LIU Xiao-juan, MENG Jian. Crystal structures and elastic properties of super hardIrN₂andIrN₃from first principles [J]. Physical Review B, 2007, 76: 054115.

[34] WANG Feng, SUN Shi-jie, YU Bo, MAO Ping-li, LIU Zheng. First-principles investigation of binary intermetallics in Mg-Al-Ca-Sn alloy: Stability, electronic structure, elastic properties and thermodynamics properties [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 203-212.

[35] PENG Ming-jun, DUAN Yong-hua, SUN Yong. Anisotropic elastic properties and electronic structure of Sr-Pb compounds [J]. Computational Materials Science, 2015, 98: 311-319.

[36] LIU Qi-jun, LIU Zheng-tang, FENG Li-ping, TIAN Hao. First-principles study of structural, elastic, electronic and optical properties of orthorhombic NaAlF₄ [J]. Computational Materials Science, 2011, 50: 2822-2827.

[37] RANGANATHAN S I, OSTOJA-STARZEWSKI M. Universal elastic anisotropy index [J]. Physical Review Letters, 2008, 101: 055504.

[38] DUAN Yong-hua, WU Zhao-yong, HUANG Bo, CHEN Shuai. Phase stability and anisotropic elastic properties of the Hf-Al intermetallics: A DFT calculation [J]. Computational Materials Science, 2015, 110: 10-19.

[39] OZYAR U F, DELIGOZ E, COLAKOGLU K. Systematic study on the anisotropic elastic properties of tetragonal XYSb (X=Ti, Zr, Hf; Y=Si, Ge) compounds [J]. Solid State Sciences, 2015, 40: 92-100.

[40] YANG Xiao-min, HOU Hua, ZHAO Yu-hong, YANG Ling, HAN Pei-de. First- principles investigation of the structural, electronic and elastic properties of Mg_xAl_4-xSr (x=0, 0.5, 1) phases [J]. Computational Materials Science, 2014, 84: 374-380.

[41] QI Lei, JIN Yu-chun, ZHAO Yun-hong, YANG Xiao-min, ZHAO Hui, HAN Pei-de. The structural, elastic, electronic properties and Debye temperature of Ni₃Mo under pressure from first-principles [J]. Journal of Alloys and Compounds, 2015, 621: 383-388.

[42] GUECHI A, MERABET A, CHEGAAR M, BOUHEMADOU A, GUECHI N. Pressure effect on the structural, elastic, electronic and optical properties of the Zintl phase KAsSn, first principles study [J]. Journal of Alloys and Compounds, 2015, 621: 219-228.

高压下U₃Si₂型AlSc₂Si₂金属间化合物的结构、力学、电子结构和光学特性的第一性原理计算

张旭东¹，王 峰²，姜 伟^1,2

1. 沈阳工业大学 理学院，沈阳 110870；

2. 沈阳工业大学 材料科学与工程学院，沈阳110870

摘  要：通过第一性原理方法计算了高压下AlSc₂Si₂金属间化学物的结构、力学、电子和光学特性。计算的弹性常数及模量表明AlSc₂Si₂在高压下保持良好的力学稳定性。将AlSc₂Si₂ 和 Al₃Sc的力学性能对比发现，AlSc₂Si₂较Al₃Sc有更高的硬度。各向异性常数和3D弹性模量图像表明AlSc₂Si₂是各向异性材料。电子结构特性表明AlSc₂Si₂具有金属的性质并且这种性质随着压力的升高而减弱。同时计算和分析了其光学性质与压强的关系。这些计算结果为进一步的实验工作提供了理论支持。

关键词：U₃Si₂型AlSc₂Si₂；力学性能；电子结构；光学性质；第一性原理计算

(Edited by Xiang-qun LI)

Foundation item: Projects (L2014051, LT2014004) supported by the Program for Scientific Technology Plan of the Educational Department of Liaoning Province, China

Corresponding author: Xu-dong ZHANG; Tel: +86-15840019002; Fax: +86-24-25496502; E-mail: sutxyz@163.com

DOI: 10.1016/S1003-6326(17)60017-7