Numerical investigations on mechanical characteristics and failure mechanism of outwash deposits based on random meso-structures using discrete element method
来源期刊:中南大学学报(英文版)2017年第12期
论文作者:张强 徐卫亚 刘沁雅 沈俊良 闫龙
文章页码:2894 - 2905
Key words:outwash deposits; random meso-structures; discrete element method; numerical tests; mechanical characteristics; failure mechanism
Abstract: Outwash deposit is a unique type of geological materials, and its features such as heterogeneity, discontinuity and nonlinearity determine the complexity of mechanical characteristics and failure mechanism. In this work, random meso-structure of outwash deposits was constructed by the technique of computer random simulation based on characteristics of its meso-structure in the statistical sense and some simplifications, and a series of large direct shear tests on numerical samples of outwash deposits with stone contents of 15%, 30%, 45% and 60% were conducted using the discrete element method to further investigate its mechanical characteristics and failure mechanism under external load. The results show that the deformation characteristics and shear strength of outwash deposits are to some extent improved with the increase of stone content, and the shear stress–shear displacement curves of outwash deposits show great differences at the post-peak stage due to the random spatial distribution and content of stones. From the mesoscopic view, normal directions of contacts between “soil” and “stone” particles undergo apparent deflection as the shear displacement continues during the shearing process, accompanying redistribution of the magnitude of contact forces during the shearing process. For outwash deposits, the shear zone formed after shear failure is an irregular stripe due to the movements of stones near the shear zone, and it expands gradually with the increase of stone content. In addition, there is an approximately linear relation between the mean increment of internal friction angle and the stone content lying between 30% and 60%, and a concave nonlinear relation between the mean increment of cohesion and stone content, which are in good agreement with the existing research results.
Cite this article as: ZHANG Qiang, XU Wei-ya, LIU Qin-ya, SHEN Jun-liang, YAN Long. Numerical investigations on mechanical characteristics and failure mechanism of outwash deposits based on random meso-structures using discrete element method [J]. Journal of Central South University, 2017, 24(12): 2894–2905. DOI:https://doi.org/10.1007/s11771-017-3703-6.
J. Cent. South Univ. (2017) 24: 2894-2905
DOI: https://doi.org/10.1007/s11771-017-3703-6

ZHANG Qiang(张强)1, 2, 4, XU Wei-ya(徐卫亚)1, 2, LIU Qin-ya(刘沁雅)3,
SHEN Jun-liang(沈俊良)1, 2, YAN Long(闫龙)1, 2
1. Key Laboratory of Geomechanics and Embankment Engineering of Ministry of Education (Hohai University), Nanjing 210098, China;
2. Research Institute of Geotechnical Engineering, Hohai University, Nanjing 210098, China;
3. Department of Physics, University of Toronto, Toronto, Ontario, M5S 1A7, Canada;
4. China Institute of Water Resources and Hydropower Research, Beijing 100048, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: Outwash deposit is a unique type of geological materials, and its features such as heterogeneity, discontinuity and nonlinearity determine the complexity of mechanical characteristics and failure mechanism. In this work, random meso-structure of outwash deposits was constructed by the technique of computer random simulation based on characteristics of its meso-structure in the statistical sense and some simplifications, and a series of large direct shear tests on numerical samples of outwash deposits with stone contents of 15%, 30%, 45% and 60% were conducted using the discrete element method to further investigate its mechanical characteristics and failure mechanism under external load. The results show that the deformation characteristics and shear strength of outwash deposits are to some extent improved with the increase of stone content, and the shear stress–shear displacement curves of outwash deposits show great differences at the post-peak stage due to the random spatial distribution and content of stones. From the mesoscopic view, normal directions of contacts between “soil” and “stone” particles undergo apparent deflection as the shear displacement continues during the shearing process, accompanying redistribution of the magnitude of contact forces during the shearing process. For outwash deposits, the shear zone formed after shear failure is an irregular stripe due to the movements of stones near the shear zone, and it expands gradually with the increase of stone content. In addition, there is an approximately linear relation between the mean increment of internal friction angle and the stone content lying between 30% and 60%, and a concave nonlinear relation between the mean increment of cohesion and stone content, which are in good agreement with the existing research results.
Key words: outwash deposits; random meso-structures; discrete element method; numerical tests; mechanical characteristics; failure mechanism
1 Introduction
Outwash deposits, as a special kind of deposits, formed by glacial movements in Quaternary Period, is widely distributed in the mountains and valleys in the west area of China. It is a type of unfavorable geological bodies commonly encountered in the large hydraulic and hydropower projects [1, 2]. As shown in Fig. 1, it is mainly composed of random-shaped rock fragments (stones) with high stiffness and strength and fine-grained soil with relatively weak stiffness and strength in terms of material composition, so it also can be viewed as a typical binary mixture medium of soil and stones (SSM), where soil and stones are respectively regarded as matrix and fillers. On the other hand, stones of different shapes and sizes, randomly distributed in the soil, constitute the internal framework of outwash deposits which is often called meso-structure of outwash deposits. Outwash deposits have more complicated mechanical characteristics and failure mechanism compared with relatively homogeneous soil and rock due to its inhomogeneity, discontinuity and randomness of meso-structure. With the rapid development of large hydropower projects in the west of China, the stability of outwash deposits slope has become a potential and huge threat to the construction and long-term safe operation of hydropower projects [3–5]. Therefore, the research on the physical and mechanical responses and failure mechanism of outwash deposits under load is of great practical significance to scientific and accurate assessment of the stability of outwash deposits slope.
Up to now, the practical methods for studying the mechanical characteristics and failure mechanism of outwash deposits as a typical binary mixture medium of soil and stones are laboratory tests, in-situ tests and numerical simulations. In recent years, many researchers [6–9] have carried out a series of studies in this respect and obtained some important results by laboratory and in-situ tests. However, due to the complexities of material composition and meso-structure of outwash deposits, the dimension-limitation of laboratory equipment, the disturbance of typical samples and size effect and so on, it is difficult to accurately reflect the physical and mechanical characteristics and failure mechanism of outwash deposits by laboratory tests. Although large in-situ tests to some extent remedy the limitations and defects of laboratory tests, great randomness and discreteness of test results and high test costs restrict the wide application of them in research. Compared with laboratory and in-situ tests, numerical simulations have been frequently used to study the mechanical characteristics and failure mechanism of outwash deposits in recent years because of its economy and effectiveness. For example, XU et al [10], DING et al [11], XU et al [12] and WANG et al [13] constructed the meso-structure of outwash deposits based on the photos at different locations in the field using digital image processing technology, and a series of numerical tests were carried out based on FEM or DEM. Some human factors are involved in the research because meso-structure constructed by digital image processing technology has a great dependence on the photos [14]. Considering the randomness of the characteristics of meso-structure for outwash deposits, many researchers have tried to reconstruct it in the statistical sense using computer random simulation technology nowadays. For instance, LI et al [15] and HE et al [16] proposed a method to reconstruct meso-structure of soil-rock mixture based on the Monte Carlo method. However, the method has significant limitations in practical applications because irregular stones are simplified as regular geometries such as circles and regular polygons. On that basis, XU et al [14] made some improvements on the method where stones are represented by arbitrary convex polygons and ellipsoids when constructing meso- structure of outwash deposits. SHI et al [17] and JIA et al [18] also conducted a series of numerical direst shear tests on the samples of outwash deposits with different stone contents under different normal stresses using PFC3D, irregular stones in the samples are represented by spheres with different sizes. As shown in Fig. 1, the shapes of stones in outwash deposits in the field are diversified and complicated, and the interlocking of particles has considerable effects on the mechanical characteristics and failure mechanism of outwash deposits under loads. Nevertheless, some important geometric features of stones such as convexity-concavity and flatness are ignored when constructing meso-structure of outwash deposits by these existing methods, leading to that there are some deviations between the research results and the actual ones.
Considering the characteristics of meso-structure of outwash deposits, a 2D modelling system of random meso-structure of outwash deposits (RMS2D) is developed based on computer random simulation technology; then numerical samples of outwash deposits with stone contents of 15%, 30%, 45% and 60% are prepared for large direct shear tests, and a series of numerical tests on the samples are carried out using PFC2D to further investigate the mechanical characteristics and shear failure mechanism.

Fig. 1 Typical photos of outwash deposits distributed on both sides of large hydropower station reservoir
2 Modelling of random meso-structure of outwash deposits
Mechanical characteristics and failure mechanism of outwash deposits are to a large extent affected by its material compositions and meso-structure. Hence, generation of random meso-structure whose structural features resemble outwash deposits in the statistical sense is the first precondition to accurately obtain mechanical characteristics and failure mechanism of outwash deposits based on numerical simulations. In this section, random meso-structure was modeled using computer random simulation technology based on the features of meso-structure of outwash deposits in the statistical sense.
2.1 Material composition
As mentioned above, outwash deposits can be viewed as a typical binary mixture of “soil” and “stone” particles, where “soil” and “stone” particles are the relative concepts. At a certain study scale, particles are regarded as “soil” rather than “stones”, depending on the threshold of “soil-stone” separation (dthr). Based on the systematic researches on such soil-stone mixture materials done by MEDLEY and LINQUIST et al [19], dthr can be defined as
 (1)
(1)
where d is the particle size, Lc is the engineering characteristic scale. For the direct shear tests, Lc is set to the minimum dimensions of the upper or bottom shear boxes and equal to 40 cm in this work, so dthr is equal to 2 cm according to Eq. (1). In addition, the maximum size of the particles should not exceed 1/5 the width of the upper or bottom shear boxes in the direct shear tests, suggested by many researchers, so it is set to 10 cm. Hence, the sizes of the “stone” particles are limited between 2.0 cm and 10 cm in the tests.
2.2 Meso-structure characteristics
The meso-structure of outwash deposits is the main framework of exterior force resistance, whose internal structural features have significant effects on its mechanical characteristics and failure mechanism. The meso-structure features of outwash deposits can be characterized by the shapes, the size and distribution, the spatial distribution and the content of stones.
2.2.1 Shapes of stones
The shapes of stones in outwash deposits are extremely complex in the field, while they are simplified properly when modelling random meso-structure of outwash deposits by the technique of computer random simulation. Since the geometric features of stones (e.g. irregularity, convexity-concavity, angularity and flatness) have a great influence on the macroscopic mechanical characteristics and failure mechanism of outwash deposits [19], some important geometry features of stones should be retained as far as possible to obtain accurate simulation results. Considering the diversified, angular and convex-concave shapes of stones, convex-concave polygons with arbitrary shapes are used to approximately represent the stones in outwash deposits in this work.
As shown in Fig. 2, for a polygon of N sides, its outline can be described by the coordinates of N vertices (θi, ri) in polar coordinate system [20]. In order to model arbitrarily shaped stones, △θi and ri are defined as two independent random variables obeying a uniform random distribution. The random variable ri can be expressed as follows:
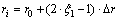 (3)
(3)
where ξ1 is a random number between [0, 1], r0 is the mean value of ri, and Δr is the amplitude value of ri.
The random variable △θi is defined as the difference of polar angles of two neighboring vertices (namely,△θi=θi+1–θi), which can be expressed as
 (4)
(4)
where ξ2 is a random number between [0, 1], δ is a variable whose value is usually set to 0.3. Normally, the sum of △θi is not equal to 2π,  In order to ensure that the generated polygons are closed, △θi needs to be adjusted as follows:
In order to ensure that the generated polygons are closed, △θi needs to be adjusted as follows: Finally, the polar angles of the vertices θi can be determined according to the relation:
Finally, the polar angles of the vertices θi can be determined according to the relation: 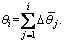 In the Cartesian coordinate system, the coordinates of vertices (xi, yi) can be determined as follows:
In the Cartesian coordinate system, the coordinates of vertices (xi, yi) can be determined as follows:
 (5)
(5)
where (x0, y0) are the central coordinates of stones.

Fig. 2 Geometric shape of arbitrary stone:
It is seen from Fig. 1 that stones in outwash deposits have flat shapes. The flatness is another important geometric feature of stones in the field. In 2D, the flatness of a stone can be defined as the ratio of the length of its major axis to that of its minor one. As shown in Fig. 3(a), the flatness of polygons generated based on the method above is close to 1.0 in general cases, which is inconsistent with the statistical flatness of stones in the field. In order to ensure that the flatness of the generated polygons coincides with the practical result in statistical sense, the polygons are stretched along their major axises or compressed along their minor axises, as shown in Fig. 2(b). In the tests, the flatness of stones is limited between [1.0, 3.0], as shown in Fig. 3(b).
2.2.2 Size and distribution of stones
The size of a stone is an important index to describe the size distribution of stones in outwash deposits. In 2D, the size of a stone is defined as the maximum distance of any two points on its outline. It is equal to the length of the major axis of a polygon in this work, as shown in Fig. 2. Superficially, stones in outwash deposits have different shapes and sizes at different locations in the field, and it seems to indicate that the meso-structure characteristics exhibit a chaotic phenomenon [19]. However, statistical analyses on the size of stones in outwash deposits show that the size distribution of stones approximately obeyed a logarithmic normal distribution [15, 21, 22]. Therefore, the size distribution of stones is assumed to obey a lognormal distribution in this work, whose probability density function is given as follows:
 (6)
(6)
where λ is the size of a stone, μ and σ are the mean and variance of the natural logarithm of the sizes of stones.
The size of a stone generated based on the method above is arbitrary. In order to ensure that the size distribution of the stones obeys a certain lognormal distribution, the stone is enlarged or shrunk in all directions so that the size is changed but the shape remains unchanged. The new coordinates of the vertices  can be determined as follows:
can be determined as follows:
 (7)
(7)
where  in which λ′ and λ are the sizes of a polygon before and after scaling.
in which λ′ and λ are the sizes of a polygon before and after scaling.
2.2.3 Spatial distribution of stones
The spatial distribution of stones has a significant influence on shear strength of outwash deposits, whose distribution feature can be characterized by the center and spatial orientation of stones. It exhibits great randomness and complexity due to complicated geological formation of outwash deposits. The centers of stones are assumed to obey a uniform random distribution in the domain of a sample when modelling random meso-structure of outwash deposits, and their coordinates can be determined as follows:
 (8)
(8)
where xmin, xmax, ymin and ymax are the minimum and maximum coordinates of the domain of a sample in the x and y axes, ηx and ηy are two independent random numbers uniformly distributed between [0, 1].
The spatial orientation of a stone can be described by an attitude angle (α), which is defined as an included angle between the major axis and right hand of the horizontal direction, as shown in Fig. 2(a). Two cases are considered in terms of the spatial orientation of stones. The first one is that the attitude angles of stones are assumed to obey a uniform random distribution between [0, 2π], as shown in Fig. 3(b). However, the major axes of stones are arranged in a preferred direction in some cases, as shown in Fig. 3(c). In such cases, the attitude angles of stones are assumed to obey a uniform random distribution between 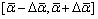 where
where  is the statistical preferred attitude angle, and △
is the statistical preferred attitude angle, and △ is the amplitude value of
is the amplitude value of  .
.
2.2.4 Content of stones
In 2D, stone content (C) is defined as the ratio of the total area of all stones in a sample to the total area of the sample, which can be expressed as
 (9)
(9)
where Ai is the area of ith stone in a sample, A is the total area of the sample.
2.3 Generation of random meso-structures
Based on the principles above, a 2D modelling system of random meso-structure for outwash deposits (RMS2D) is developed using FORTRAN programming language, which provides a powerful technical support for numerical tests later. As shown in Fig. 3, several random meso-structures with different features are generated for outwash deposits based on RMS2D.
3 Numerical simulations of large direct shear tests
3.1 Direct shear apparatus
In order to consider relatively large stones in the samples of outwash deposits and eliminate the size effect of its shear strength parameters, a large direct shear apparatus was used in the numerical tests, as shown in Fig. 4. It consists of upper and bottom shear boxes with the same dimensions of 60 cm×40 cm (width×height), where the upper one is surrounded by four walls of 3#, 4#, 5# and 6# and the bottom one is surrounded by four walls of 1#, 2#, 7# and 8#. During the direct shear tests, the lateral walls of upper shear boxes (4#, and 6#) were fixed, and all walls of the bottom shear box were moved together at a slow speed of 0.0005 m/s, meanwhile keeping a constant normal stress on the bottom wall of the bottom shear box (1#) and the top wall of the upper shear box (5#) via servo mechanism [23], as shown in Fig. 4. In order to obtain the shear strength of samples with different stone contents, samples were carried out under three different normal stresses of 300 kPa, 500 kPa and 800 kPa, respectively.
3.2 Preparation of numerical samples
Before the direct shear tests using PFC2D, numerical samples of outwash deposits with different stone contents are prepared first. In the samples, “soil” particles are represented by circular balls, and irregular and random-shaped “stone” particles are represented by clumps of slaved balls in which the relative positions of balls remain fixed and contacts between balls are ignored in calculation cycles [23].
Based on the principle above, a method of preparation of numerical samples is proposed for outwash deposits, as shown in Fig. 5. It includes two steps: a model of balls with the same dimensions of the large direct shear apparatus is generated to represent “pure” soil first, as shown in Fig. 5(a), and it is made up of 12086 balls where the maximum and minimum radii of the balls are 4.0 mm and 2.5 mm, respectively; then, numerical samples of outwash deposits are generated based on meso-structures with different stone contents using RMS2D, as shown in Fig. 5(b). The basic principle is that all polygons in the random meso-structure are checked whether balls are contained in each of them and these balls are clumped together into a clump.

Fig. 3 Random meso-structures of different features generated for outwash deposits based on RMS2D:

Fig. 4 Large apparatus for numerical direct shear tests

Fig. 5 Preparation of numerical samples for outwash deposits:
In order to investigate the effects of stone content on mechanical characteristics and failure mechanism of outwash deposits, samples with different stone contents of 15%, 30%, 45% and 60% were prepared before numerical tests, as shown in Fig. 7. Moreover, considering the randomness of the spatial distribution of stones, five samples with different spatial distributions of stones were prepared for each stone content, as shown in Fig. 8.
3.3 Mesoscopic constitutive relations at contacts and parameters
In the discrete element method, the macroscopic physical and mechanical behaviours of materials are simulated by the mesoscopic constitutive relations at contacts between particles [24]. In PFC2D, the constitutive relations at each contact include three parts: contact stiffness model, slip model and bond model.
3.3.1 Contact stiffness model
When two particles are in contact, the contact stiffness model defines the relation between the contact force and the relative displacement in both normal and tangential directions, which can be expressed as
 (9)
(9)
where  is the normal contact force, Kn is the normal stiffness, Un is the total normal displacement,
is the normal contact force, Kn is the normal stiffness, Un is the total normal displacement,  is the increment of the tangential contact force, ks is the tangential stiffness, and ΔUs is the increment of the tangential displacement. In the linear contact stiffness model, if the normal and tangential stiffnesses of two particles (marked by A and B) at a contact are expressed as
is the increment of the tangential contact force, ks is the tangential stiffness, and ΔUs is the increment of the tangential displacement. In the linear contact stiffness model, if the normal and tangential stiffnesses of two particles (marked by A and B) at a contact are expressed as  and
and 
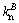 and
and  respectively, Kn and ks can be determined as follows:
respectively, Kn and ks can be determined as follows:
 (10)
(10)
3.3.2 Slip model
Slip model defines the relation between normal and tangential contact forces and allows slip to occur by limiting the tangential contact force. When the tangential contact force at a contact exceeds the maximum allowable tangential contact force, the relative slip occurs at the contact, which can be described as
 (11)
(11)
where 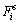 is the tangential contact force,
is the tangential contact force,  is the maximum allowable tangential contact force,
is the maximum allowable tangential contact force,  where μ is the friction coefficient.
where μ is the friction coefficient.
3.3.3 Bond model
In the bond model, particles are allowed to be bonded together by glue at contacts. Normally, the glue has a certain strength, and it is broken when the contact force is greater than its strength. There are two types of bond model in PFC2D: contact bond model and parallel bond model. In this work, the contact bond model is adopted to simulate the mesoscopic behaviour of the glue at a contact [11, 16, 17], and its normal and tangential strengths are expressed as  and
and  in the model.
in the model.
As the mesoscopic parameters of constitutive relations at contacts cannot be determined directly by the macroscopic parameters obtained by the tests in laboratory such as elastic modulus, Poisson ratio, internal friction angle and cohesion, they are often calibrated directly by matching the curves of numerical tests with those of laboratory tests [25, 26]. As shown in Fig. 6, the mesoscopic parameters of “soil” particles are obtained by calibrating the curves of indoor direct shear tests, and those of “stone” particles are determined based on the calibration method proposed by YOON et al [27]. The mesoscopic parameters of “soil” and “stone” particles are listed in Table 1.
4 Analysis of numerical simulation results
4.1 Curves of shear stress and shear displacement
The effects of stone content on the deformational and mechanical characteristics of outwash deposits were analyzed thoroughly by comparing the shear stress–shear displacement curves of samples with different stone contents. Figure 7 shows the shear stress–shear displacement curves of samples with different stone contents (15%, 30%, 45% and 60%) under different normal stresses (300 kPa, 500 kPa and 800 kPa). It is obviously seen from Fig. 7 that the shear stress–shear displacement curves undergo two different stages of pre- and post-peak, which is consistent with the results of large in-situ direct shear tests on soil-rock mixtures [28].
At the pre-peak stage, the shear stress–shear displacement curves of samples with different contents exhibit a similar shape. By and large, the shear stress increases gradually as the shear displacement continues, and a convex and nonlinear relation exists between the shear stress and shear displacement. On the other hand, with the increase of stone content, the shear stress of samples increases under the same normal stress when it reaches the peak, while the shear displacements reduce. It indicates that stiffness and strength of outwash deposits are improved under external load with the increase of stone content. Comparing with the shear stress–shear displacement curves of “pure” soil sample (C=0%), stone content has little effects on the deformational and mechanical characteristics at a low stone content such as C=15%, while it has significant influences on them at a high stone content such as C=60%. The main reason is that the deformational and mechanical characteristics of outwash deposits are to a large extent determined by soil at a low stone content because stones work just as loose filler, while they are determined by stones at a high stone content as stones constitute the main framework of outwash deposits to resist external load.
At the post-peak stage, the shear stress–shear displacement curves of samples with different stone contents exhibit different shapes, which are considerably affected by the content and the spatial distribution of stones. Specifically, the shear stress–shear displacement curves of samples with low stone content such as C≤30% exhibit the phenomenon of strain softening, indicating that the shear stress decreases as the shear displacement continues gradually; the shear stress–shear displacement curves of samples with high stone content such as C≥45% may exhibit strain softening or stain hardening, depending on the normal stress and the spatial distribution of stones [28]. Figure 8 shows the shear stress–shear displacement curves of the samples with 45% stone content and different spatial distributions of stones under the same normal stress. Due to the different spatial distributions of stones, the phenomenon of strain softening is obvious for Sample 4 at the post-peak stage, while the phenomenon of strain hardening is obvious for Sample 5. It is found from Fig. 7(d) that the phenomenon of strain hardening appears under the normal stress of 500 kPa at the post-peak stage while the phenomenon of strain softening does under the normal stress of 300 kPa and 800 kPa.

Fig. 6 Direct shear tests of “pure soil”:
Table 1 Mesoscopic parameters of constitutive relations for “soil” and “stone” particles


Fig. 7 Shear stress–shear displacement curves of samples with different stone contents under different normal stresses:
In order to study the influence of the spatial distribution of stones on the deformational and mechanical characteristics of outwash deposits, five samples with different spatial distributions of stones were prepared for each of stone contents (15%, 30%, 45% and 60%). Figure 8 shows the shear stress–shear displacement curves of five samples with the stone content of 45% under the same normal stress. It is clearly seen from Fig. 8 that the shear stress–shear displacement curves have extremely similar shapes at the pre-peak stage while they exhibit great differences in shape at the post-peak stage, which indicates that the deformational and mechanical characteristics of outwash deposits are affected more considerately by the spatial distribution of stones at the post-peak stage than at the pre-peak stage. It also indicates indirectly that the deformational and mechanical characteristics of outwash deposits are more complicated than those of relatively homogeneous soil and rock [13, 19].

Fig. 8 Shear stress–displacement curves of outwash deposits samples with the same content and different spatial distributions of stones
4.2 Shear failure mechanism
From the mesoscopic view, shear failure mechanism of outwash deposit can be investigated based on the evolution of contact forces between “soil” and “stone” particles during the shearing process and the distribution of cracks after shear failure. Figure 9 shows the evolution of contact forces in the sample with the stone content of 30% during the shearing process. Figure 10 shows the distribution of cracks in the samples with the stone contents of 15%, 30%, 45% and 60% after shear failure.
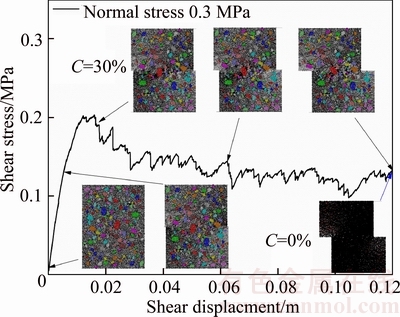
Fig. 9 Evolution of contact force chain between particles during shearing process

Fig. 10 Distribution of cracks of samples with different stone contents after shear failure:
It is found from Fig. 9 that the distribution of contact forces between “soil” and “stone” particles is uniform at the initial stage of numerical tests, which indicates that the shear stress is borne by both soil and stones and distributed evenly in them. As the shear displacement continues, the directions of contact forces near the shear zone undergo apparent deflection due to resistance to external load, leading to the change of the distribution of contact forces, and more shear stress is borne by stones than soil at last stage of numerical tests. In addition, it is found by comparing the positions of stones at different stages of tests that the stones near the shear zone experience some movements such as translation, rotation and turnover during the shear process, accompanying the release of strain energy owing to the redistribution of the positions of stones.
In the discrete element simulations, the scope of the distribution of cracks after shear failure can be viewed as the shear zone of a sample. It is clearly seen from Fig. 7 that the shear zones of the samples with different stone contents are located in a certain domain near the interface of the upper and lower shear boxes. As shown in Fig. 6(b), the shear zone of “pure soil” sample (C=0%) is a regular stripe which is approximately parallel to the interface of upper and lower shear boxes. However, the shear zones of the samples with different stone contents from 15% to 60% are irregular stripes due to the complicated movement of stones during the shear process, as shown in Fig. 7. With the increase of stone content, the shear zone expands gradually, and the phenomenon of the rounding stones in the shear zone is more obvious, which are in good agreement with the results of large in-situ direct shear tests [9].
4.3 Shear strength
In order to reduce the influence of random spatial distribution of stones on the shear strength of outwash deposits with a certain stone content, the average shear strength of samples with an identical stone content is regarded as the shear strength of outwash deposits. The shear strength parameters of outwash deposits with different stone contents are obtained according to the data of numerical tests, as listed in Table 2.
Table 2 Shear strength parameters of outwash deposits with different stone contents

As can be clearly seen from Table 2, the shear strength parameters of outwash deposits such as the internal friction angle and cohesion increase with the increase of stone content. In order to further study the influence of stone content on the shear strength parameters, the shear strength parameters of pure soil (C=0%) obtained by the direct shear tests in laboratory are set as initial standard values, and the relation between the increment of the shear strength parameters and stone content is investigated. It is found from Fig. 11 that although the increments of the internal friction angle and cohesion fluctuate within a certain range due to the random spatial distribution of stones under the same stone content, they exhibit a certain regularity with the increase of stone content on the whole. To be specific, an increasing linear relation exists between stone content and the mean increment of internal friction angle, which is consistent with previous studies [7, 19, 29, 30], as shown in Fig. 11(a). As shown in Fig. 11(b), an increasing nonlinear relationship exists between stone content and the mean increment of cohesion, and the incremental changes of cohesion increase gradually with the increase of stone content, which is consistent with the results of direct shear tests in laboratory in Ref. [31].

Fig. 11 Relations between shear strength parameters and stone content:
5 Conclusions
1) The shear stress–shear displacement curves of the samples of outwash deposits with different stone contents from 15% to 60% experience two different stages of pre- and post-peak. The shear stress–shear displacement curves have extremely similar shapes at the pre-peak stage, while they show great differences in shape at the post-peak stage, which are affected significantly by the spatial distribution and content of stones. For example, the shear stress–shear displacement curve of outwash deposits exhibits the phenomenon of strain softening under low stone content such as C≤30% at the post-peak stage, while it may exhibit the phenomenon of strain hardening under high stone content such as C≥30%.
2) From the mesoscopic view, shear failure mechanism of outwash deposits is more complicated than pure soil. For pure soil, the shear zone is a regular stripe which is approximately parallel to the interface of upper and lower shear boxes, while it is an extremely irregular stripe for outwash deposits owing to the movements of stones during the shearing process such as translation, rotation and turnover of stones. In addition, the shear zone of outwash deposits expands gradually with the increase of stone content, and the phenomenon of rounding stones in the shear zone is more obvious, which are consistent with the results of large in-situ direct shear tests.
3) The spatial distribution and content of stones have significant effects on the shear strength of outwash deposits. Although the increments of the internal friction angle and cohesion fluctuate within a certain range under the same stone content owing to the random spatial distribution of stones in outwash deposits, their mean values show a good regularity with the increase of stone content by and large. Specially, an increasing linear relation exists between stone content and the mean increment of the internal friction angle, while an increasing nonlinear relationship exists between stone content and the mean increment of cohesion, and the incremental change of cohesion increases gradually with the increase of stone content.
References
[1] XU Wei-ya, ZHANG Qiang, ZHANG Jiu-chang, WANG Ru-bin, WANG Ren-kun. Deformation and control engineering related to huge landslide on left bank of Xiluodu reservoir, south-west China [J]. European Journal of Environmental and Civil Engineering, 2013, 17: s249–s268.
[2] XU Wei-ya, ZHANG Qiang, WANG Ru-bin, WANG Huan-ling, WANG Ren-kun, XIE Wei-chao. Mechanism of continuous movement and long-term safety analysis of Baitieba landslide based on field monitoring data and numerical simulation [J]. European Journal of Environmental and Civil Engineering, 2015, 19: s140–s154.
[3] WANG Huan-ling, XU Wei-ya. Stability of Liangshuijing landslide under variation water levels of Three Gorges Reservoir [J]. European Journal of Environmental and Civil Engineering, 2013, 17: s158–s177.
[4] ZHANG Y, XU W Y, SHAO J F, ZOU L F, SUN H K. Comprehensive assessment and global stabilization measures of a large landslide in hydropower engineering [J]. European Journal of Environmental and Civil Engineering, 2013, 17(3): 154–175.
[5] ZHOU Jia-wen, XU Wei-ya, YANG Xing-guo, SHI Chong, YANG Zhao-hui. The 28 October 1996 landslide and analysis of the stability of the current Huashiban slope at the Liangjiaren Hydropower Station, Southwest China [J]. Engineering Geology, 2010, 114(1): 45–56.
[6] LINDQUIST E S, GOODMAN R E. Strength and deformation properties of a physical model mélange [C]// 1st North American Rock Mechanics Symposium. American Rock Mechanics Association, 1994: 843–850.
[7] Lindquist E S. The strength and deformation properties of mélange [D]. Berkeley, USA: University of California, 1994.
[8] Vallejo L E, Mawby R. Porosity influence on the shear strength of granular material–clay mixtures [J]. Engineering Geology, 2000, 58(2): 125–136.
[9] XU Wen-Jie, XU Qiang, HU Rui-lin. Study on the shear strength of soil–rock mixture by large scale direct shear test [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1235–1247. (in Chinese)
[10] XU Wen-Jie, HU Rui-lin, YUE Zhong-qi, ZHANG Rui, WANG Guo-liang. Research on relationship between rock block proportion and shear strength of soil-rock mixtures based on digital image analysis and large direct shear test [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(5): 996–1007. (in Chinese)
[11] DING Xiu-li, LI Yao-xu, WANG Xin. Particle flow modeling mechanical properties of soil and rock mixtures based on digital image [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 477–484. (in Chinese)
[12] XU An-quan, XU Wei-ya, SHI Chong, XIA Zhi-hao. Discrete element simulation of composite geomaterial talus deposit based on digital image technology [C]// Applied Mechanics and Materials. 2011, 55: 125–131.
[13] WANG Sheng-nian, XU Wei-ya, SHI Chong, ZHANG Qiang. Numerical simulation of direct shear tests on mechanical properties of talus deposits based on self-adaptive PCNN digital image processing [J]. Journal of Central South University, 2014, 21(7): 2904–2914.
[14] XU Wen-jie, HU Rui-lin, YUE Zhong-qi. Development of random mesostructure generating system of soil-rock mixture and study of its mesostructural mechanics based on numerical test [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1652–1665. (in Chinese)
[15] LI Xiao, LIAO Qiu-lin, HE Jian-ming. In-situ tests and a stochastic structural model of rock and soil aggregate in the three gorges reservoir area, China [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(sup1): 702–707.
[16] HE Jian-ming, LI Xiao, LI Shou-ding, GU Jin-lue. Numerical study of rock-soil aggregate by discrete element modeling [C]// Sixth International Conference on Fuzzy Systems and Knowledge Discovery. IEEE, 2009: 565–569.
[17] SHI Chong, WANG Sheng-nian, LIU Lin, MENG Qing-xiang, ZHANG Qiang. Mesomechanical simulation of direct shear test on outwash deposits with granular discrete element method [J]. Journal of Central South University, 2013, 20(4): 1094–1102.
[18] JIA Xue-ming, CHAI He-jun, ZHENG Ying-ren. Mesomechanics research of large direct shear test on soil and rock aggregate mixture with particle flow code simulation [J]. Rock and Soil Mechanics, 2010, 31(9): 2695–2703. (in Chinese)
[19] MEDLEY E V, LINDQUIST E S. The engineering significance of the scale-independence of some Franciscan mélanges in California, USA [C]// Proceedings of the 35th US rock mechanics symposium. Rotterdam: Balkema, 1995: 907–914.
[20] XU Wen-jie, YUE Zhong-qi, HU Rui-lin. Study on the mesostructure and mesomechanical characteristics of the soil–rock mixture using digital image processing based finite element method [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 749–762.
[21] WANG Zong-min, KWAN A K H, CHAN H C. Mesoscopic study of concrete I: generation of random aggregate structure and finite element mesh [J]. Computers & Structures, 1999, 70(5): 533–544.
[22] HE Jian-ming. Study of deformation and failure mechanisms of soil/rock mixtures in Three Gorges reservoir area [D]. Beijing, China: University of Mining and Technology (Beijing), 2004.
[23] YOU Xin-hua. Stochastic structural model of the earth-rock aggregate and its application [D]. Beijing, China: Beijing Jiaotong University, 2001.
[24] Itasca Consulting Group Inc. PFC2D (Particle flow code in 2 dimensions) (Version 3.1) [R]. Minneapolis: Itasca Consulting Group Inc., 2004.
[25] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies [J]. Geotechnique, 1979, 29(1): 47–65.
[26] COETZEE C J, ELS D N J. Calibration of granular material parameters for DEM modelling and numerical verification by blade–granular material interaction [J]. Journal of Terramechanics, 2009, 46(1): 15–26.
[27] YOON J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871–889.
[28] XU Wen-jie, HU Rui-lin, TAN R J. Some geomechanical properties of soil–rock mixtures in the Hutiao Gorge area, China [J]. Geotechnique, 2007, 57(3): 255–264.
[29] IRFAN T Y, TANG K Y. Effect of the coarse fractions on the shear strength of colluvium [M]. Hong Kong: Geotechnical Engineering Office, Civil Engineering Department, 1993.
[30] MEDLEY E W. Systematic characterization of mélange bimrocks and other chaotic soil/rock mixtures [J]. Felsbau, 1999, 17(3): 152–162.
[31] LI Wei-shu, WU Ai-qing, DING Xiu-li. Study on influencing factors of shear strength parameters of slide zone clay in three Gorges Reservoir area [J]. Rock and Soil Mechanics, 2006, 27(1): 56–60. (in Chinese)
(Edited by FANG Jing-hua)
Cite this article as: ZHANG Qiang, XU Wei-ya, LIU Qin-ya, SHEN Jun-liang, YAN Long. Numerical investigations on mechanical characteristics and failure mechanism of outwash deposits based on random meso-structures using discrete element method [J]. Journal of Central South University, 2017, 24(12): 2894–2905. DOI:https://doi.org/10.1007/s11771-017-3703-6.
Foundation item: Project(2011CB013504) supported by the National Basic Research Program (973 Program) of China; Project(2013BAB06B01) supported by the National Science & Technology Pillar Program during the Twelfth Five-year Plan Period; Projects(11772118, 51479049, 51709282) supported by the National Natural Science Foundation of China; Project(2017M620838) supported by the Postdoctoral Science Foundation of China; Project(487237) supported by the Natural Sciences and Engineering Research Council of Canada
Received date: 2016-01-24; Accepted date: 2016-05-25
Corresponding author: ZHANG Qiang, PhD; Tel: +86–18310524890; E-mail: zhangq@iwhr.com

